Hostname: page-component-745bb68f8f-v2bm5 Total loading time: 0 Render date: 2025-01-14T20:35:24.095Z Has data issue: false hasContentIssue false
  • English
  • Français

The symmetric draining of capillary liquids from containers with interior corners

Published online by Cambridge University Press:  26 November 2018

Mark M. Weislogel Open the ORCID record for Mark M. Weislogel [Opens in a new window]  and
Joshua T. McCraney
Mark M. Weislogel*
Affiliation:
Department of Mechanical and Materials Engineering, Portland State University, PO Box 751, Portland, OR 97207, USA
Joshua T. McCraney
Affiliation:
Department of Mechanical and Materials Engineering, Portland State University, PO Box 751, Portland, OR 97207, USA
*
†Email address for correspondence: mmw@cecs.pdx.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

A new lubrication model solution is found for the late-stage draining of a wetting capillary liquid from a linear interior corner. The solution exploits the symmetry of volumetric sink conditions at opposing ends of such a ‘double-drained’ interior corner flow with applications ranging from liquid recovery in microfluidic devices on Earth to liquid fuel scavenging in large fuel tanks aboard spacecraft. At long times $t$, the nominal liquid depth is 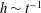$h\sim t^{-1}$, the liquid volume is 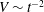$V\sim t^{-2}$ and the maximum volumetric liquid removal rate is 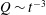$Q\sim t^{-3}$. The constraints under which the solution is valid are provided. To qualitatively assess the value of the solution, representative experiments are conducted at larger length scales aboard the International Space Station and at microfluidic length scales in a terrestrial laboratory. Both sets of experiments confirm the predicted power-law dependences. We show that the separation of variables solution offers a method to predict maximum drain rates from related geometries where a single drain location provides the required symmetry of the problem.

JFM classification

Interfacial Flows (free surface): Capillary flows Interfacial Flows (free surface): Interfacial Flows (free surface) Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 902 - 920
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bico, J. & Quéré, D. 2002 Rise of liquids and bubble in angular capillary tubes. J. Colloid Interface Sci. 247, 162–166.Google Scholar
Bolleddula, D. A. & Weislogel, M. M.2009 Capillary corner flows with partial and nonwetting fluids. Tech. Rep. NASA/CR-2009-215672, Glenn Research Center, Cleveland, OH.Google Scholar
Bowen, M. & King, J. 2013 Dynamics of a viscous thread on a non-planar substrate. J. Engng Maths 80 (1), 39–62.Google Scholar
Bunnel, C. T. & Weislogel, M. M.2018, The capillary flow experiments aboard the International Space Station. NASA Technical Memorandum (to appear), URL http://psi.nasa.gov.Google Scholar
Chato, D. J. & Martin, T. A. 2006 Vented tank resupply experiment: flight test results. J. Spacecr. Rockets 43 (5), 1124–1130.Google Scholar
Chen, Y., Weislogel, M. M. & Nardin, C. 2006 Capillary-driven flows along rounded interior corners. J. Fluid Mech. 566, 235–271.Google Scholar
Concus, P. & Finn, R. 1969 On the behavior of a capillary free surface in a wedge. Proc. Natl Acad. Sci. 63, 292–299.Google Scholar
Dangla, R., Kayi, S. C. & Baroud, C. N. 2013 Droplet microfluidics driven by gradients of confinement. Proc. Natl Acad. Sci. 110, 853–858.Google Scholar
Dong, M. & Chatzis, I. 1995 The imbibition and flow of a wetting liquid along the corners of a square capillary tube. J. Colloid Interface Sci. 172 (2), 278–288.Google Scholar
Fries, N. & Dreyer, M. 2008 The transition from inertial to viscous flow in capillary rise. J. Colloid Interface Sci. 327 (1), 125–128.Google Scholar
Jaekle, D. E.1991 Propellant management device conceptual design and analysis: vanes. AIAA-91-2172, 27th AIAA/SAE/ASME/ASEE Joint Propulsion Conference, June 24–26, Sacramento, California, United States.Google Scholar
Jenson, R. M., Wollman, A., Weislogel, M., Sharp, L., Green, R., Canfield, P., Klatte, J. & Dreyer, M. 2014 Passive phase separation of microgravity bubbly flows using conduit geometry. Intl J. Multiphase Flow 65, 68–81.Google Scholar
Khare, K., Brinkmann, M., Bruce, M., Law, B. M., Gurevich, E. L., Herminghaus, S. & Seemann, R. 2007 Dewetting of liquid filaments in wedge-shaped grooves. Langmuir 23, 12138–12141.Google Scholar
Klatte, J., Haake, D., Weislogel, M. M. & Dreyer, M. E. 2008 A fast numerical procedure for steady capillary flow in open capillary channels. Acta Mech. 201, 269–276.Google Scholar
Langbein, D. 1990 The shape and stability of liquid menisci at solid edges. J. Fluid Mech. 213, 251–265.Google Scholar
Langbein, D. 2002 Capillary Surfaces: Shape – Stability – Dynamics, in Particular under Weightlessness, Springer Tracts in Modern Physics, vol. 178. Springer.Google Scholar
Li, Y. Q. & Liu, L. 2014 A study of capillary flow in variable interior corners under microgravity. Acta Phys. Sinica 63 (21), 214704.Google Scholar
Litterst, C., Eccarius, S., Hebling, C., Zengerle, R. & Koltay, P. 2006 Increasing μDMFC efficiency by passive CO2 bubble removal and discontinuous operation. J. Micromech. Microengng. 16, 248–253.Google Scholar
Melin, J., van der Wijngaart, W. & Stemme, G. 2005 Behaviour and design considerations for continuous flow closed-open-closed liquid microchannels. Lab on a Chip 5, 682–686.Google Scholar
Metz, T., Paust, N., Zengerle, R. & Koltay, P. 2012 Capillary driven movement of gas bubbles in tapered structures. Microfluid. Nanofluid. 9 (2), 341–355.Google Scholar
Oberg, J. 2006 Breathing easy in space is never easy: problems with oxygen generators aboard the space station could have big implications. IEEE Spectrum.Google Scholar
Ponomarenko, A., Clanet, C. & Quéré, D. 2011 Capillary rise in wedges. J. Fluid Mech. 666, 146–154.Google Scholar
Quéré, D. 1997 Inertial capillarity. Europhys. Lett. 39, 533–538.Google Scholar
Quéré, D. 1999 Rebounds in a capillary tube. Langmuir 1, 3679–3682.Google Scholar
Ramé, E. & Weislogel, M. M. 2009 Gravity effects on capillary flows in sharp corners. Phys. Fluids 21 (4), 042106.Google Scholar
Ransohoff, T. C. & Radke, C. J. 1988 Laminar flow of a wetting liquid along the corners of a predominantly gas-occupied noncircular pore. J. Colloid Interface Sci. 121 (2), 392–401.Google Scholar
Reyssat, E. 2014 Drops and bubbles in wedges. J. Fluid Mech. 748, 641–662.Google Scholar
Romero, L. A. & Yost, F. G. 1996 Flow in an open channel capillary. J. Fluid Mech. 322, 109–129.Google Scholar
Rosendahl, U., Ohlhoff, A. & Dreyer, M. E. 2004 Choked flows in open capillary channels: theory, experiment and computations. J. Fluid Mech. 518, 187–214.Google Scholar
Stocker, R. & Hosoi, A. 2005 Lubrication in a corner. J. Fluid Mech. 544, 353–377.Google Scholar
Viestenz, K. J., Weislogel, M. M. & Sargusingh, M. J. 2018 Capillary structures for exploration life support ISS experiment kit. In 48th International Conference on Environmental Systems (ICES-2008-241), pp. 1–11. Texas Tech University.Google Scholar
Wang, C. X., Xu, S. H., Sun, Z. W. & Hu, W. R. 2010 A study of the influence of initial liquid volume on the capillary flow in an interior corner under microgravity. Intl J. Heat Mass Transfer 53 (9–10), 1801–1807.Google Scholar
Weislogel, M. M. 2001 Capillary flow in interior corners: the infinite corner. Phys. Fluids 13 (11), 3101–3107.Google Scholar
Weislogel, M. M. 2003 Some analytical tools for fluids management in space: isothermal capillary flows along interior corners. Adv. Space Res. 32 (2), 163–170.Google Scholar
Weislogel, M. M. 2012 Compound capillary rise. J. Fluid Mech. 709, 622–647.Google Scholar
Weislogel, M. M., Jenson, R., Chen, Y., Collicott, S. H., Klatte, J. & Dreyer, M.2007 The capillary flow experiments aboard the International Space Station. In 58th International Astronautical Congress, Hyderabad, India, paper IAC-07-A2.6.02.Google Scholar
Weislogel, M. M. & Lichter, S. 1996 A spreading drop in an interior corner: theory and experiment. Microgravity Sci. Technol. IX, 175–184.Google Scholar
Weislogel, M. M. & Lichter, S. 1998 Capillary flow in an interior corner. J. Fluid Mech. 373, 349–378.Google Scholar
Weislogel, M. M. & Nardin, C. L. 2005 Capillary driven flow along interior corners formed by planar walls of varying wettability. Microgravity Sci. Technol. 17 (3), 45–55.Google Scholar
Weislogel, M. M., Collicott, S. H., Gotti, D. J., Bunnell, C. T., Kurta, C. E. & Golliher, E. L. 2004 The capillary flow experiments: handheld fluids experiments for International Space Station. In 42nd AIAA Aerospace Sci. Meeting and Exhibit, Reno, NV, AIAA 2004-1148, pp. 7408–7414. American Institute of Aeronautics and Astronautics.Google Scholar
Weislogel, M. M., Chen, Y., Collicott, S. H., Bunnell, C. T., Green, R. D. & Bohman, D. Y. 2009 More handheld fluid interface experiments for the International Space Station (CFE-2). In 47th AIAA Aerospace Sciences Meeting, Orlando, AIAA-2009-0615, pp. 1–10. American Institute of Aeronautics and Astronautics.Google Scholar
Weislogel, M. M., Baker, J. A. & Jenson, R. M. 2011 Quasi-steady capillarity driven flow. J. Fluid Mech. 685, 271–305.Google Scholar
Wu, Z. H., Huang, Y. Y., Chen, X. Q. & Zhang, X. 2018 Capillary-driven flows along curved interior corners. Intl J. Multiphase Flow 109, 14–25.Google Scholar