Article contents
Systematic errors of skin-friction measurements by oil-film interferometry
Published online by Cambridge University Press: 21 May 2015
Abstract
In recent years, the independent measurement of wall shear stress with oil-film or oil-drop interferometry has become a cornerstone of turbulent-boundary-layer research as many arguments depend critically on a precise knowledge of the skin friction 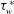 ${\it\tau}_{w}^{\ast }$. To our knowledge, all practitioners of oil-drop interferometry have so far used the leading-order similarity solution for asymptotically thin, wedge-shaped, two-dimensional oil films established by Tanner & Blows (J. Phys. E: Sci. Instrum., vol. 9, 1976, pp. 194–202) to relate the evolution of drop thickness to
${\it\tau}_{w}^{\ast }$. To our knowledge, all practitioners of oil-drop interferometry have so far used the leading-order similarity solution for asymptotically thin, wedge-shaped, two-dimensional oil films established by Tanner & Blows (J. Phys. E: Sci. Instrum., vol. 9, 1976, pp. 194–202) to relate the evolution of drop thickness to 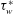 ${\it\tau}_{w}^{\ast }$. It is generally believed that this procedure, if carefully implemented, yields the true time-averaged
${\it\tau}_{w}^{\ast }$. It is generally believed that this procedure, if carefully implemented, yields the true time-averaged 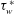 ${\it\tau}_{w}^{\ast }$ within
${\it\tau}_{w}^{\ast }$ within 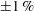 $\pm 1\,\%$ or possibly better, but the systematic errors due to the finite thickness of the oil film have never been determined. They are analysed here for oil films with a thickness of the order of a viscous unit in a zero-pressure-gradient turbulent boundary layer. Neglecting spanwise surface curvature and surface tension effects, corrections due to the secondary air boundary layer above the oil film are derived with a linearised triple-layer approach that accounts for the turbulent shear-stress perturbation by means of modified van-Driest-type closure models. In addition, the correction due to processing oil drops with a slight streamwise surface curvature as if they were exact wedges is quantified. Both corrections are evaluated for oil-drop interferograms acquired in a zero-pressure-gradient turbulent boundary layer at a Reynolds number of around 3500, based on displacement thickness, and are shown to produce a reduction of the friction velocity relative to the basic Tanner and Blows theory of between
$\pm 1\,\%$ or possibly better, but the systematic errors due to the finite thickness of the oil film have never been determined. They are analysed here for oil films with a thickness of the order of a viscous unit in a zero-pressure-gradient turbulent boundary layer. Neglecting spanwise surface curvature and surface tension effects, corrections due to the secondary air boundary layer above the oil film are derived with a linearised triple-layer approach that accounts for the turbulent shear-stress perturbation by means of modified van-Driest-type closure models. In addition, the correction due to processing oil drops with a slight streamwise surface curvature as if they were exact wedges is quantified. Both corrections are evaluated for oil-drop interferograms acquired in a zero-pressure-gradient turbulent boundary layer at a Reynolds number of around 3500, based on displacement thickness, and are shown to produce a reduction of the friction velocity relative to the basic Tanner and Blows theory of between 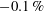 $-0.1\,\%$ and
$-0.1\,\%$ and 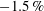 $-1.5\,\%$, depending on the mixing-length model. Despite the uncertainty about the true correction, the analysis allows the formulation of some guidelines on where and when to analyse interference fringes in order to minimise the error on the measured wall shear stress.
$-1.5\,\%$, depending on the mixing-length model. Despite the uncertainty about the true correction, the analysis allows the formulation of some guidelines on where and when to analyse interference fringes in order to minimise the error on the measured wall shear stress.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
References
- 17
- Cited by



