1 Introduction
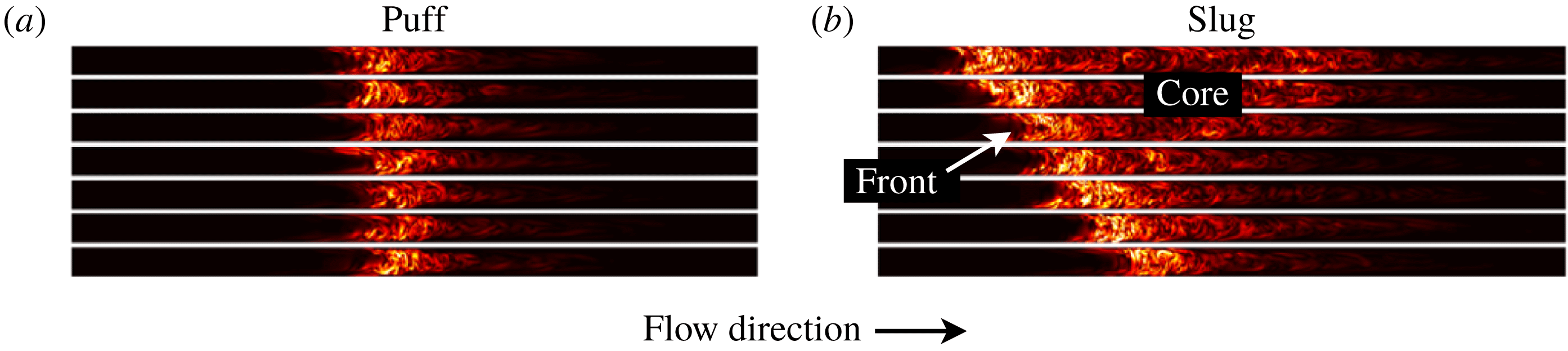
The route to turbulence in pipe flow is subcritical, meaning that turbulence can be initiated and sustained even though laminar flow remains linearly stable. At the lowest flow rates for which it can be successfully triggered (Reynolds numbers of approximately 2000), turbulence takes the form of localised patches known as puffs. A typical puff is illustrated in figure 1(a). Try as one might, it is simply impossible to produce extended regions of sustained turbulence in pipe flow at these ‘low’ Reynolds numbers. The situation changes at higher Reynolds numbers, as illustrated in figure 1(b). Localised patches of turbulence expand and now it is impossible to have a flow that is eventually anything other than fully turbulent. Expanding turbulent patches are known as slugs. Puffs and slugs are the key players in transitional pipe flow and have been the subject of numerous experimental and numerical studies, (Lindgren Reference Lindgren1969; Wygnanski & Champagne Reference Wygnanski and Champagne1973; Darbyshire & Mullin Reference Darbyshire and Mullin1995; Nishi et al.
Reference Nishi, Ünsal, Durst and Biswas2008; Shimizu & Kida Reference Shimizu and Kida2009; Duguet, Willis & Kerswell Reference Duguet, Willis and Kerswell2010; Hof et al.
Reference Hof, de Lozar, Avila, Tu and Schneider2010; Barkley et al.
Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015; Song et al.
Reference Song, Barkley, Hof and Avila2017), to cite just a few.
Figure 1. Evolution of (a) a localised puff at
 $Re=2000$
and (b) a slug at
$Re=2000$
and (b) a slug at
 $Re=2600$
. Time evolves in the upward direction. Dark areas correspond to laminar flow and bright areas correspond to turbulent fluctuations. The flow is from left to right and visualisations are in a co-moving reference frame to keep the turbulent structures centred. Reproduced from Song et al. (Reference Song, Barkley, Hof and Avila2017).
$Re=2600$
. Time evolves in the upward direction. Dark areas correspond to laminar flow and bright areas correspond to turbulent fluctuations. The flow is from left to right and visualisations are in a co-moving reference frame to keep the turbulent structures centred. Reproduced from Song et al. (Reference Song, Barkley, Hof and Avila2017).
As a consequence of the strongly subcritical character of pipe flow, fluid motion is in one of two distinct states, turbulent or laminar, and these are separated by turbulent–laminar fronts where the flow switches between the two. The significance of these fronts was recognised as far back as Coles (Reference Coles1962). Of particular importance here is the intense upstream front (left-hand front) seen in figure 1(b). Essentially, the kinetic energy contained within the laminar upstream flow is fuel for this front. The front ‘burns this fuel’, converting laminar kinetic energy into turbulent kinetic energy (TKE). Dissipation increases downstream from the front and after a short distance dissipation and production of TKE come into balance and form the core of the slug – or what is just called turbulent pipe flow once it fully occupies the pipe. The intense upstream front is call a strong front.
To understand the puff, consider what happens to the slug as the Reynolds number is decreased, that is viscosity increased. There comes a point where TKE production in the core can no longer balance the increased dissipation due to the increase in viscosity. The core collapses. However, at the strong front production is still large and so it survives the increase in viscosity. The strong front becomes the puff – an isolated front continually ‘burning’ upstream laminar kinetic energy but leaving no persistent downstream turbulent wake. (The transition from slug to puff can be viewed as a transition from bistability to excitability (Barkley Reference Barkley2011, Reference Barkley2016; Barkley et al.
Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015; Graham Reference Graham2015).)
Finally, the issue that has captured much attention in recent years is the fate of puffs on long time scales. Puffs are metastable structures that ultimately either decay (revert to laminar flow) or split (initiate a second puff downstream). Collectively these two processes determine a critical point for a percolation transition (Avila et al.
Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011). Below the critical point, puff decay is more frequent than puff splitting and eventually the flow is entirely laminar. Above the critical point, puff splitting is the more frequent process and turbulence is sustained in a highly intermittent form.
2 Overview
In their recent paper, Rinaldi, Canton & Schlatter (Reference Rinaldi, Canton and Schlatter2019) address how the classical puffs and slugs of straight pipe flow are transformed in the case of bent pipes, and more broadly how the subcritical route to turbulence is potentially affected by the presence of pipe curvature. Specifically, the authors perform direct numerical simulations of flow in toroidal pipe with pipe-to-torus-diameter ratio of
 $\unicode[STIX]{x1D6FF}=0.01$
. The immediate, striking observation is that the strong turbulent–laminar fronts, so dominant in straight pipes, vanish even for such a moderately curved pipe. Visually the fronts in straight and curved pipes are unmistakably different. See the lead image of this commentary as well as the movies attached to the original article. In a straight pipe, an intense concentration of vortices abruptly forms at the upstream front, while in the curved pipe vortices emerge gradually from laminar flow. Quantitatively, in the curved pipe the TKE production at the upstream front is barely larger than its value in the slug core, while for the straight pipe the production at a strong front is about five times that of the core. Velocity fluctuations at the upstream front are also greatly curtailed in the curved pipe, even though fluctuations in the slug core attain similar values for straight and curved pipes. As could then be expected from the connection between puffs and fronts, puffs exhibit a dramatic reduction in intensity in bents pipes. Interestingly though, their streamwise extent is about twice that of puffs in a straight pipe.
$\unicode[STIX]{x1D6FF}=0.01$
. The immediate, striking observation is that the strong turbulent–laminar fronts, so dominant in straight pipes, vanish even for such a moderately curved pipe. Visually the fronts in straight and curved pipes are unmistakably different. See the lead image of this commentary as well as the movies attached to the original article. In a straight pipe, an intense concentration of vortices abruptly forms at the upstream front, while in the curved pipe vortices emerge gradually from laminar flow. Quantitatively, in the curved pipe the TKE production at the upstream front is barely larger than its value in the slug core, while for the straight pipe the production at a strong front is about five times that of the core. Velocity fluctuations at the upstream front are also greatly curtailed in the curved pipe, even though fluctuations in the slug core attain similar values for straight and curved pipes. As could then be expected from the connection between puffs and fronts, puffs exhibit a dramatic reduction in intensity in bents pipes. Interestingly though, their streamwise extent is about twice that of puffs in a straight pipe.
Through an examination of the energy budget in the pipe cross-section, Rinaldi et al. show that there is a significant localisation of TKE production toward the outer bend of the pipe, consistent with early experimental observations by Sreenivasan & Strykowski (Reference Sreenivasan and Strykowski1983). The authors argue, convincingly, that the secondary flow (Dean Reference Dean1927) generated in the curved pipe is responsible for this localisation, and moreover, that due to this localisation, turbulence in the front can be sustained at smaller energies than is the case for a straight pipe, thereby explaining why and how strong fronts vanish in a bent pipe. To be clear, owing in part to the numerous applications of curved pipe flow, there is a substantial literature on instabilities and turbulence in helical and toroidal pipes (see the discussion and citations in Kühnen et al. (Reference Kühnen, Braunshier, Schwegel, Kuhlmann and Hof2015) and Rinaldi et al. (Reference Rinaldi, Canton and Schlatter2019)), and the secondary Dean flow is well known to play an important role in bent pipes. However, Rinaldi et al. are the first to demonstrate its important role in the energy budget, not only at turbulent–laminar fronts and also in the turbulent core within toroidal pipe flow.
Potentially the most interesting observations in Rinaldi et al. (Reference Rinaldi, Canton and Schlatter2019) concern the way pipe curvature affects the route to turbulence. It is known from Kühnen et al. (Reference Kühnen, Braunshier, Schwegel, Kuhlmann and Hof2015) that in toroidal pipes with pipe-to-torus-diameter ratio greater than about
 $\unicode[STIX]{x1D6FF}=0.028$
, the transition scenario switches from subcritical to supercritical. At
$\unicode[STIX]{x1D6FF}=0.028$
, the transition scenario switches from subcritical to supercritical. At
 $\unicode[STIX]{x1D6FF}=0.01$
, still considerably away from the supercritical scenario, Rinaldi et al. observe that, in comparison with straight pipes, there is a substantial reduction in the range of Reynolds numbers over which a potential percolation transition could take place. Most significantly, the authors failed to detect any puff splitting events in the range of parameters considered. This could be due to a mundane increase in timescales for splitting, caused for some as yet unknown reason. However, Rinaldi et al. have shown that puff lengths and intensities are substantially affected by pipe curvature, so this observation (or rather lack of observation of puff splitting), could also be indicative of a modification of the subcritical scenario by which turbulence first becomes sustained.
$\unicode[STIX]{x1D6FF}=0.01$
, still considerably away from the supercritical scenario, Rinaldi et al. observe that, in comparison with straight pipes, there is a substantial reduction in the range of Reynolds numbers over which a potential percolation transition could take place. Most significantly, the authors failed to detect any puff splitting events in the range of parameters considered. This could be due to a mundane increase in timescales for splitting, caused for some as yet unknown reason. However, Rinaldi et al. have shown that puff lengths and intensities are substantially affected by pipe curvature, so this observation (or rather lack of observation of puff splitting), could also be indicative of a modification of the subcritical scenario by which turbulence first becomes sustained.
3 Future
We know from work by Kühnen et al. (Reference Kühnen, Braunshier, Schwegel, Kuhlmann and Hof2015) that there is a cross-over from a subcritical to a supercritical transition in toroidal pipes as the pipe curvature increases. Moreover, we know from Canton, Schlatter & Örlü (Reference Canton, Schlatter and Örlü2016) precisely where toroidal pipe flow becomes linearly unstable as a function of curvature. What we do not know is what happens to the established subcritical scenario in straight pipes as the curvature is increased, and how this eventually gives way to a supercritical scenario commencing with a linear instability. The present paper takes a step towards answering this, but it also provides as many questions as answers on this fundamental issue. Fortunately, toroidal pipe flow has a well-defined ‘knob’, pipe curvature, that can and should be turned in whatever steps are needed to address this.
On a more general note, we now understand what to simulate and what to analyse in order to quantify turbulent–laminar fronts in wall-bounded shear flows. This applies not only to straight and bent pipes, but to a great many other shear flows where intermittency precedes fully turbulent flow. From simulation data we can compute energy budgets and we can obtain front speeds, critical Reynolds numbers and many other facts. What we cannot do at present is obtain any of these from the governing Navier–Stokes equations, other than by performing large-scale direct numerical simulations. The most important long-term goal in this area then is the derivation, through some properly justified approximations, of expressions for front dynamics directly from the Navier–Stokes equations. This is perhaps too much to hope for, but we know that on a qualitative, and even semi-quantitative level the dynamics of turbulent–laminar fronts is relatively simple (Barkley et al.
Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015) and this gives some hope. There are many practical reasons to pursue such a theory, but independently of those reasons, fronts between different states are always interesting, and when one of the two states is turbulent flow, they are especially fascinating.
$Re=2000$ and (b) a slug at
$Re=2600$. Time evolves in the upward direction. Dark areas correspond to laminar flow and bright areas correspond to turbulent fluctuations. The flow is from left to right and visualisations are in a co-moving reference frame to keep the turbulent structures centred. Reproduced from Song et al. (2017).


1 Introduction
The route to turbulence in pipe flow is subcritical, meaning that turbulence can be initiated and sustained even though laminar flow remains linearly stable. At the lowest flow rates for which it can be successfully triggered (Reynolds numbers of approximately 2000), turbulence takes the form of localised patches known as puffs. A typical puff is illustrated in figure 1(a). Try as one might, it is simply impossible to produce extended regions of sustained turbulence in pipe flow at these ‘low’ Reynolds numbers. The situation changes at higher Reynolds numbers, as illustrated in figure 1(b). Localised patches of turbulence expand and now it is impossible to have a flow that is eventually anything other than fully turbulent. Expanding turbulent patches are known as slugs. Puffs and slugs are the key players in transitional pipe flow and have been the subject of numerous experimental and numerical studies, (Lindgren Reference Lindgren1969; Wygnanski & Champagne Reference Wygnanski and Champagne1973; Darbyshire & Mullin Reference Darbyshire and Mullin1995; Nishi et al. Reference Nishi, Ünsal, Durst and Biswas2008; Shimizu & Kida Reference Shimizu and Kida2009; Duguet, Willis & Kerswell Reference Duguet, Willis and Kerswell2010; Hof et al. Reference Hof, de Lozar, Avila, Tu and Schneider2010; Barkley et al. Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015; Song et al. Reference Song, Barkley, Hof and Avila2017), to cite just a few.
Figure 1. Evolution of (a) a localised puff at $Re=2000$
and (b) a slug at
$Re=2000$
and (b) a slug at
 $Re=2600$
. Time evolves in the upward direction. Dark areas correspond to laminar flow and bright areas correspond to turbulent fluctuations. The flow is from left to right and visualisations are in a co-moving reference frame to keep the turbulent structures centred. Reproduced from Song et al. (Reference Song, Barkley, Hof and Avila2017).
$Re=2600$
. Time evolves in the upward direction. Dark areas correspond to laminar flow and bright areas correspond to turbulent fluctuations. The flow is from left to right and visualisations are in a co-moving reference frame to keep the turbulent structures centred. Reproduced from Song et al. (Reference Song, Barkley, Hof and Avila2017).
As a consequence of the strongly subcritical character of pipe flow, fluid motion is in one of two distinct states, turbulent or laminar, and these are separated by turbulent–laminar fronts where the flow switches between the two. The significance of these fronts was recognised as far back as Coles (Reference Coles1962). Of particular importance here is the intense upstream front (left-hand front) seen in figure 1(b). Essentially, the kinetic energy contained within the laminar upstream flow is fuel for this front. The front ‘burns this fuel’, converting laminar kinetic energy into turbulent kinetic energy (TKE). Dissipation increases downstream from the front and after a short distance dissipation and production of TKE come into balance and form the core of the slug – or what is just called turbulent pipe flow once it fully occupies the pipe. The intense upstream front is call a strong front.
To understand the puff, consider what happens to the slug as the Reynolds number is decreased, that is viscosity increased. There comes a point where TKE production in the core can no longer balance the increased dissipation due to the increase in viscosity. The core collapses. However, at the strong front production is still large and so it survives the increase in viscosity. The strong front becomes the puff – an isolated front continually ‘burning’ upstream laminar kinetic energy but leaving no persistent downstream turbulent wake. (The transition from slug to puff can be viewed as a transition from bistability to excitability (Barkley Reference Barkley2011, Reference Barkley2016; Barkley et al. Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015; Graham Reference Graham2015).)
Finally, the issue that has captured much attention in recent years is the fate of puffs on long time scales. Puffs are metastable structures that ultimately either decay (revert to laminar flow) or split (initiate a second puff downstream). Collectively these two processes determine a critical point for a percolation transition (Avila et al. Reference Avila, Moxey, de Lozar, Avila, Barkley and Hof2011). Below the critical point, puff decay is more frequent than puff splitting and eventually the flow is entirely laminar. Above the critical point, puff splitting is the more frequent process and turbulence is sustained in a highly intermittent form.
2 Overview
In their recent paper, Rinaldi, Canton & Schlatter (Reference Rinaldi, Canton and Schlatter2019) address how the classical puffs and slugs of straight pipe flow are transformed in the case of bent pipes, and more broadly how the subcritical route to turbulence is potentially affected by the presence of pipe curvature. Specifically, the authors perform direct numerical simulations of flow in toroidal pipe with pipe-to-torus-diameter ratio of $\unicode[STIX]{x1D6FF}=0.01$
. The immediate, striking observation is that the strong turbulent–laminar fronts, so dominant in straight pipes, vanish even for such a moderately curved pipe. Visually the fronts in straight and curved pipes are unmistakably different. See the lead image of this commentary as well as the movies attached to the original article. In a straight pipe, an intense concentration of vortices abruptly forms at the upstream front, while in the curved pipe vortices emerge gradually from laminar flow. Quantitatively, in the curved pipe the TKE production at the upstream front is barely larger than its value in the slug core, while for the straight pipe the production at a strong front is about five times that of the core. Velocity fluctuations at the upstream front are also greatly curtailed in the curved pipe, even though fluctuations in the slug core attain similar values for straight and curved pipes. As could then be expected from the connection between puffs and fronts, puffs exhibit a dramatic reduction in intensity in bents pipes. Interestingly though, their streamwise extent is about twice that of puffs in a straight pipe.
$\unicode[STIX]{x1D6FF}=0.01$
. The immediate, striking observation is that the strong turbulent–laminar fronts, so dominant in straight pipes, vanish even for such a moderately curved pipe. Visually the fronts in straight and curved pipes are unmistakably different. See the lead image of this commentary as well as the movies attached to the original article. In a straight pipe, an intense concentration of vortices abruptly forms at the upstream front, while in the curved pipe vortices emerge gradually from laminar flow. Quantitatively, in the curved pipe the TKE production at the upstream front is barely larger than its value in the slug core, while for the straight pipe the production at a strong front is about five times that of the core. Velocity fluctuations at the upstream front are also greatly curtailed in the curved pipe, even though fluctuations in the slug core attain similar values for straight and curved pipes. As could then be expected from the connection between puffs and fronts, puffs exhibit a dramatic reduction in intensity in bents pipes. Interestingly though, their streamwise extent is about twice that of puffs in a straight pipe.
Through an examination of the energy budget in the pipe cross-section, Rinaldi et al. show that there is a significant localisation of TKE production toward the outer bend of the pipe, consistent with early experimental observations by Sreenivasan & Strykowski (Reference Sreenivasan and Strykowski1983). The authors argue, convincingly, that the secondary flow (Dean Reference Dean1927) generated in the curved pipe is responsible for this localisation, and moreover, that due to this localisation, turbulence in the front can be sustained at smaller energies than is the case for a straight pipe, thereby explaining why and how strong fronts vanish in a bent pipe. To be clear, owing in part to the numerous applications of curved pipe flow, there is a substantial literature on instabilities and turbulence in helical and toroidal pipes (see the discussion and citations in Kühnen et al. (Reference Kühnen, Braunshier, Schwegel, Kuhlmann and Hof2015) and Rinaldi et al. (Reference Rinaldi, Canton and Schlatter2019)), and the secondary Dean flow is well known to play an important role in bent pipes. However, Rinaldi et al. are the first to demonstrate its important role in the energy budget, not only at turbulent–laminar fronts and also in the turbulent core within toroidal pipe flow.
Potentially the most interesting observations in Rinaldi et al. (Reference Rinaldi, Canton and Schlatter2019) concern the way pipe curvature affects the route to turbulence. It is known from Kühnen et al. (Reference Kühnen, Braunshier, Schwegel, Kuhlmann and Hof2015) that in toroidal pipes with pipe-to-torus-diameter ratio greater than about $\unicode[STIX]{x1D6FF}=0.028$
, the transition scenario switches from subcritical to supercritical. At
$\unicode[STIX]{x1D6FF}=0.028$
, the transition scenario switches from subcritical to supercritical. At
 $\unicode[STIX]{x1D6FF}=0.01$
, still considerably away from the supercritical scenario, Rinaldi et al. observe that, in comparison with straight pipes, there is a substantial reduction in the range of Reynolds numbers over which a potential percolation transition could take place. Most significantly, the authors failed to detect any puff splitting events in the range of parameters considered. This could be due to a mundane increase in timescales for splitting, caused for some as yet unknown reason. However, Rinaldi et al. have shown that puff lengths and intensities are substantially affected by pipe curvature, so this observation (or rather lack of observation of puff splitting), could also be indicative of a modification of the subcritical scenario by which turbulence first becomes sustained.
$\unicode[STIX]{x1D6FF}=0.01$
, still considerably away from the supercritical scenario, Rinaldi et al. observe that, in comparison with straight pipes, there is a substantial reduction in the range of Reynolds numbers over which a potential percolation transition could take place. Most significantly, the authors failed to detect any puff splitting events in the range of parameters considered. This could be due to a mundane increase in timescales for splitting, caused for some as yet unknown reason. However, Rinaldi et al. have shown that puff lengths and intensities are substantially affected by pipe curvature, so this observation (or rather lack of observation of puff splitting), could also be indicative of a modification of the subcritical scenario by which turbulence first becomes sustained.
3 Future
We know from work by Kühnen et al. (Reference Kühnen, Braunshier, Schwegel, Kuhlmann and Hof2015) that there is a cross-over from a subcritical to a supercritical transition in toroidal pipes as the pipe curvature increases. Moreover, we know from Canton, Schlatter & Örlü (Reference Canton, Schlatter and Örlü2016) precisely where toroidal pipe flow becomes linearly unstable as a function of curvature. What we do not know is what happens to the established subcritical scenario in straight pipes as the curvature is increased, and how this eventually gives way to a supercritical scenario commencing with a linear instability. The present paper takes a step towards answering this, but it also provides as many questions as answers on this fundamental issue. Fortunately, toroidal pipe flow has a well-defined ‘knob’, pipe curvature, that can and should be turned in whatever steps are needed to address this.
On a more general note, we now understand what to simulate and what to analyse in order to quantify turbulent–laminar fronts in wall-bounded shear flows. This applies not only to straight and bent pipes, but to a great many other shear flows where intermittency precedes fully turbulent flow. From simulation data we can compute energy budgets and we can obtain front speeds, critical Reynolds numbers and many other facts. What we cannot do at present is obtain any of these from the governing Navier–Stokes equations, other than by performing large-scale direct numerical simulations. The most important long-term goal in this area then is the derivation, through some properly justified approximations, of expressions for front dynamics directly from the Navier–Stokes equations. This is perhaps too much to hope for, but we know that on a qualitative, and even semi-quantitative level the dynamics of turbulent–laminar fronts is relatively simple (Barkley et al. Reference Barkley, Song, Mukund, Lemoult, Avila and Hof2015) and this gives some hope. There are many practical reasons to pursue such a theory, but independently of those reasons, fronts between different states are always interesting, and when one of the two states is turbulent flow, they are especially fascinating.