Hostname: page-component-78c5997874-mlc7c Total loading time: 0 Render date: 2024-11-10T23:26:22.318Z Has data issue: false hasContentIssue false
  • English
  • Français

Taylor dispersion in osmotically driven laminar flows in phloem

Published online by Cambridge University Press:  02 March 2021

M. Nakad Open the ORCID record for M. Nakad [Opens in a new window] ,
T. Witelski Open the ORCID record for T. Witelski [Opens in a new window] ,
J. C. Domec Open the ORCID record for J. C. Domec [Opens in a new window] ,
S. Sevanto Open the ORCID record for S. Sevanto [Opens in a new window]  and
G. Katul Open the ORCID record for G. Katul [Opens in a new window]
M. Nakad*
Affiliation:
Nicholas School of the Environment, Duke University, Durham, NC27708, USA
T. Witelski
Affiliation:
Department of Mathematics, Duke University, Durham, NC27708-0320, USA
J. C. Domec
Affiliation:
Nicholas School of the Environment, Duke University, Durham, NC27708, USA UMR 1391, INRA-ISPA, Bordeaux Sciences Agro, 33175, Gradignan Cedex, France
S. Sevanto
Affiliation:
Earth and Environmental Sciences Division, Los Alamos National Laboratory, Los Alamos, NM87545, USA
G. Katul
Affiliation:
Nicholas School of the Environment, Duke University, Durham, NC27708, USA Department of Civil and Environmental Engineering, Duke University, Durham, NC27708, USA
*
†Email address for correspondence: mazen.nakad@duke.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

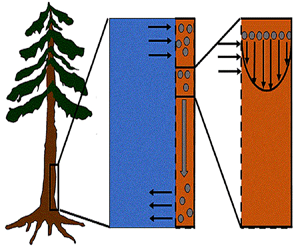
Sucrose is among the main products of photosynthesis that are deemed necessary for plant growth and survival. It is produced in the mesophyll cells of leaves and translocated to different parts of the plant through the phloem. Progress in understanding this transport process remains fraught with experimental difficulties, thereby prompting interest in theoretical approaches and laboratory studies. The Münch pressure and mass flow model is one of the accepted hypotheses describing the physics of sucrose transport in the phloem. It is based on osmosis creating an energy potential difference between the source and the sink. The flow responding to this energy potential is assumed laminar and described by the Hagen–Poiseuille equation. This study revisits such osmotically driven flows in tubes with membrane walls by including the effects of Taylor dispersion on mass transport. This effect has been overlooked in phloem flow studies. Taylor dispersion can increase the effective transport of solutes by increasing the apparent diffusion coefficient. It is shown that, in addition to the conventional diffusive correction derived for impermeable tube walls, a new adjustment to the mean advective terms arises because of osmotic effects. Because the molecular Schmidt number is very large for sucrose in water, the sucrose front speed and travel times have a direct dependence on the Péclet number for different ranges of the Münch number. This study establishes upper limits on expected Taylor dispersion enhancement of sucrose transport.

JFM classification

Biological Fluid Dynamics: Biological Fluid Dynamics Low-Reynolds-number flows: Low-Reynolds-number flows Low-Reynolds-number flows: Lubrication theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 913 , 25 April 2021 , A44
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aldis, G.K. 1988 The unstirred layer during osmotic flow into a tubule. Bull. Math. Biol. 50 (5), 531–545.CrossRefGoogle ScholarPubMed
van Bel, A.J.E. 2003 The phloem, a miracle of ingenuity. Plant Cell Environ. 26 (1), 125–149.CrossRefGoogle Scholar
Cabrita, P., Thorpe, M. & Huber, G.J. 2013 Hydrodynamics of steady state phloem transport with radial leakage of solute. Front. Plant Sci. 4, 531.CrossRefGoogle ScholarPubMed
Christy, A.L. & Ferrier, J.M. 1973 A mathematical treatment of Münch's pressure-flow hypothesis of phloem translocation. Plant Physiol. 52 (6), 531–538.CrossRefGoogle ScholarPubMed
Curtis, O.F. & Scofield, H.T. 1933 A comparison of osmotic concentrations of supplying and receiving tissues and its bearing on the Münch hypothesis of the translocation mechanism. Am. J. Bot. 20 (7), 502–512.CrossRefGoogle Scholar
Fensom, D.S. 1981 Problems arising from a Münch-type pressure flow mechanism of sugar transport in phloem. Can. J. Bot. 59 (4), 425–432.CrossRefGoogle Scholar
Haaning, L.S., Jensen, K.H., Hélix-Nielsen, C., Berg-Sørensen, K. & Bohr, T. 2013 Efficiency of osmotic pipe flows. Phys. Rev. E 87 (5), 053019.CrossRefGoogle ScholarPubMed
Henton, S.M., Greaves, A.J., Piller, G.J. & Minchin, P.E.H. 2002 Revisiting the Münch pressure–flow hypothesis for long-distance transport of carbohydrates: modelling the dynamics of solute transport inside a semipermeable tube. J. Expl Bot. 53 (373), 1411–1419.Google ScholarPubMed
Housley, T.L. & Fisher, D.B. 1977 Estimation of osmotic gradients in soybean sieve tubes by quantitative autoradiography: qualified support for the Münch hypothesis. Plant Physiol. 59 (4), 701–706.CrossRefGoogle ScholarPubMed
Huang, C.W., Domec, J.C., Palmroth, S., Pockman, W.T., Litvak, M.E. & Katul, G.G. 2018 Transport in a coordinated soil-root-xylem-phloem leaf system. Adv. Water Resour. 119, 1–16.CrossRefGoogle Scholar
Iberall, A.S. & Schindler, A.M. 1973 Physics of Membrane Transport, vol. 2. General Technical Services.Google Scholar
Jensen, K.H. 2018 Phloem physics: mechanisms, constraints, and perspectives. Curr. Opin. Plant Biol. 43, 96–100.CrossRefGoogle Scholar
Jensen, K.H., Berg-Sørensen, K., Bruus, H., Holbrook, N.M., Liesche, J., Schulz, A., Zwieniecki, M.A & Bohr, T. 2016 Sap flow and sugar transport in plants. Rev. Mod. Phys. 88 (3), 035007.CrossRefGoogle Scholar
Jensen, K.H., Berg-Sørensen, K., Friis, S.M.M. & Bohr, T. 2012 Analytic solutions and universal properties of sugar loading models in Münch phloem flow. J. Theor. Biol. 304, 286–296.CrossRefGoogle ScholarPubMed
Jensen, K.H., Bohr, T. & Bruus, H. 2010 Self-consistent unstirred layers in osmotically driven flows. J. Fluid Mech. 662, 197–208.CrossRefGoogle Scholar
Jensen, K.H., Lee, J., Bohr, T., Bruus, H., Holbrook, N.M. & Zwieniecki, M.A. 2011 Optimality of the Münch mechanism for translocation of sugars in plants. J. R. Soc. Interface 8 (61), 1155–1165.CrossRefGoogle ScholarPubMed
Jensen, K.H., Rio, E., Hansen, R., Clanet, C. & Bohr, T. 2009 Osmotically driven pipe flows and their relation to sugar transport in plants. J. Fluid Mech. 636, 371–396.CrossRefGoogle Scholar
King, J.R. & Please, C.P. 1986 Diffusion of dopant in crystalline silicon: an asymptotic analysis. IMA J. Appl. Maths 37 (3), 185–197.CrossRefGoogle Scholar
Knoblauch, M., Knoblauch, J., Mullendore, D.L., Savage, J.A., Babst, B.A., Beecher, S.D., Dodgen, A.C., Jensen, K.H. & Holbrook, N.M. 2016 Testing the Münch hypothesis of long distance phloem transport in plants. Elife 5, e15341.CrossRefGoogle ScholarPubMed
Knoblauch, M. & Oparka, K. 2012 The structure of the phloem: still more questions than answers. Plant J. 70 (1), 147–156.CrossRefGoogle ScholarPubMed
Knoblauch, M. & Peters, W.S. 2017 What actually is the Münch hypothesis? A short history of assimilate transport by mass flow. J. Integr. Plant Biol. 59 (5), 292–310.CrossRefGoogle Scholar
Konrad, W., Katul, G., Roth-Nebelsick, A. & Jensen, K.H. 2018 Xylem functioning, dysfunction and repair: a physical perspective and implications for phloem transport. Tree Physiol. 39 (2), 243–261.CrossRefGoogle Scholar
Lang, A. 1983 Turgor-regulated translocation. Plant Cell Environ. 6 (9), 683–689.Google Scholar
Mencuccini, M. & Hölttä, T. 2010 The significance of phloem transport for the speed with which canopy photosynthesis and belowground respiration are linked. New Phytol. 185 (1), 189–203.CrossRefGoogle ScholarPubMed
Minchin, P.E.H. & Lacointe, A. 2005 New understanding on phloem physiology and possible consequences for modelling long-distance carbon transport. New Phytol. 166 (3), 771–779.CrossRefGoogle ScholarPubMed
Münch, E. 1930 Stoffbewegungen in der Pflanze. G. Fischer.Google Scholar
Nikinmaa, E., Hölttä, T., Hari, P., Kolari, P., Mäkelä, A., Sevanto, S. & Vesala, T. 2013 Assimilate transport in phloem sets conditions for leaf gas exchange. Plant Cell Environ. 36 (3), 655–669.CrossRefGoogle ScholarPubMed
Pedley, T.J. 1983 Calculation of unstirred layer thickness in membrane transport experiments: a survey. Q. Rev. Biophys. 16 (2), 115–150.CrossRefGoogle ScholarPubMed
Phillips, R.J. & Dungan, S.R. 1993 Asymptotic analysis of flow in sieve tubes with semi-permeable walls. J. Theor. Biol. 162 (4), 465–485.CrossRefGoogle Scholar
Pickard, W.F. & Abraham-Shrauner, B. 2009 A ‘simplest’ steady-state Münch-like model of phloem translocation, with source and pathway and sink. Funct. Plant Biol. 36 (7), 629–644.CrossRefGoogle Scholar
Rand, R.H. 1983 Fluid mechanics of green plants. Annu. Rev. Fluid Mech. 15 (1), 29–45.CrossRefGoogle Scholar
Ryan, M.G. & Asao, S. 2014 Phloem transport in trees. Tree Physiol. 34 (1), 1–4.CrossRefGoogle ScholarPubMed
Savage, J.A., Beecher, S.D., Clerx, L., Gersony, J.T., Knoblauch, J., Losada, J.M., Jensen, K.H., Knoblauch, M. & Holbrook, N.M. 2017 Maintenance of carbohydrate transport in tall trees. Nat. Plants 3 (12), 965–972.CrossRefGoogle ScholarPubMed
Sevanto, S. 2018 Drought impacts on phloem transport. Curr. Opin. Plant Biol. 43, 76–81.CrossRefGoogle ScholarPubMed
Spanner, D.C. 1958 The translocation of sugar in sieve tubes. J. Expl Bot. 9 (3), 332–342.CrossRefGoogle Scholar
Taylor, G.I. 1953 Dispersion of soluble matter in solvent flowing slowly through a tube. Proc. R. Soc. Lond. A 219 (1137), 186–203.Google Scholar
Thompson, M.V. & Holbrook, N.M. 2003 a Application of a single-solute non-steady-state phloem model to the study of long-distance assimilate transport. J. Theor. Biol. 220 (4), 419–455.CrossRefGoogle Scholar
Thompson, M.V. & Holbrook, N.M. 2003 b Scaling phloem transport: water potential equilibrium and osmoregulatory flow. Plant Cell Environ. 26 (9), 1561–1577.CrossRefGoogle Scholar
Turgeon, R. 2010 The puzzle of phloem pressure. Plant Physiol. 154 (2), 578–581.CrossRefGoogle ScholarPubMed
Wardlaw, I.F. 1974 Phloem transport: physical chemical or impossible. Annu. Rev. Plant Physiol. 25 (1), 515–539.CrossRefGoogle Scholar
Weir, G.J. 1981 Analysis of Münch theory. Math. Biosci. 56 (1–2), 141–152.CrossRefGoogle Scholar