Hostname: page-component-7dd5485656-6kn8j Total loading time: 0 Render date: 2025-10-31T05:38:38.018Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermal boundary layer structure in turbulent Rayleigh–Bénard convection in a rectangular cell

Published online by Cambridge University Press:  13 March 2013

Quan Zhou  and
Ke-Qing Xia
Quan Zhou
Affiliation:
Shanghai Institute of Applied Mathematics and Mechanics, Shanghai University, Shanghai 200072, China Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
Ke-Qing Xia*
Affiliation:
Department of Physics, The Chinese University of Hong Kong, Shatin, Hong Kong, China
*
†Email address for correspondence: kxia@phy.cuhk.edu.hk
Get access Rights & Permissions [Opens in a new window]

Abstract

We report high-spatial-resolution measurements of the thermal boundary layer (BL) properties in turbulent thermal convection. The experiment was made near the lower conducting plate of a water-filled rectangular convection cell of height 0.76 m, with a Prandtl number 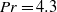$\mathit{Pr}= 4. 3$ and over the Rayleigh-number range 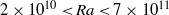$2\times 1{0}^{10} \lt \mathit{Ra}\lt 7\times 1{0}^{11} $ . Time series of the local temperature at various vertical distance $z$ from the plate were measured. Statistical properties of the profiles of the temperature, i.e. the mean temperature 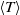$\langle T\rangle $ , fluctuating temperature root mean square (r.m.s.) 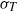${\sigma }_{T} $ , temperature skewness 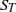${S}_{T} $ , and flatness 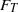${F}_{T} $ , and those of the temperature time derivative, i.e. the r.m.s. 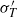${ \sigma }_{T}^{\prime } $ , skewness 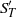${ S}_{T}^{\prime } $ and flatness ${ F}_{T}^{\prime } $ of the derivative, are studied. It is found that most of these quantities exhibit some degree of invariability with 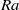$\mathit{Ra}$ , especially for the regime inside the thermal BL. When comparing with the mean temperature profiles, the profiles of the second moment of temperature seem to possess a higher level of universality. It is shown that the distance 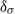${\delta }_{\sigma } $ from the plate to the maximal temperature r.m.s. position provides a natural length scale for the characterization of the thermal BL, as the statistical properties of the temperature field, such as its r.m.s., skewness and flatness, are all sharply different below and above this length scale, i.e. below 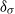${\delta }_{\sigma } $ , 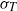${\sigma }_{T} $ increases linearly with the vertical distance $z$ from the plate and 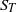${S}_{T} $ is close to zero and 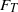${F}_{T} $ is close to three and both quantities remains nearly constant, whereas above 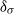${\delta }_{\sigma } $ the decay of 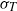${\sigma }_{T} $ obeys a logarithmic behaviour and 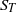${S}_{T} $ and 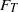${F}_{T} $ both exhibit a hill-like structure. It is also found that near the plate 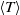$\langle T\rangle $ , 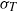${\sigma }_{T} $ and 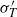${ \sigma }_{T}^{\prime } $ all increase linearly with $z$ . Our observations further reveal that such linear dependence occurs within a self-similar region of the thermal BL, where the temperature probability density functions can be scaled onto a single distribution that differs slightly from the Gaussian distribution. The 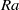$\mathit{Ra}$ -dependencies of various thermal BL properties are also studied and our results yield 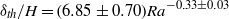${\delta }_{th} / H= (6. 85\pm 0. 70){\mathit{Ra}}^{- 0. 33\pm 0. 03} $ , 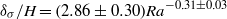${\delta }_{\sigma } / H= (2. 86\pm 0. 30){\mathit{Ra}}^{- 0. 31\pm 0. 03} $ and 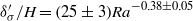${ \delta }_{\sigma }^{\prime } / H= (25\pm 3){\mathit{Ra}}^{- 0. 38\pm 0. 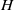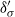05} $ , where $H$ is the height of the cell, ${\delta }_{th} $ and ${ \delta }_{\sigma }^{\prime } $ are the BL thicknesses determined respectively from the profiles of 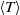$\langle T\rangle $ and 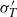${ \sigma }_{T}^{\prime } $ .

JFM classification

Boundary Layers: Boundary layer structure Turbulent Flows: Turbulent convection

Information

Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 199 - 224
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Article purchase

Temporarily unavailable

References

Adrian, R. J. 1996 Variation of temperature and velocity fluctuations in turbulent thermal convection over horizontal surfaces. Intl J. Heat Mass Transfer 39, 2303–2310.CrossRefGoogle Scholar
Ahlers, G., Bodenschatz, E., Funfschilling, D., Grossmann, S., He, X.-Z., Lohse, D., Stevens, R. J. A. M. & Verzicco, R. 2012 Logarithmic temperature profiles in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 109, 114501.Google Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81, 503–537.Google Scholar
Ahlers, G. & Xu, X.-C. 2001 Prandtl-number dependence of heat transport in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 86, 3320–3323.CrossRefGoogle ScholarPubMed
Ashkenazi, S. & Steinberg, V. 1999 High Rayleigh number turbulent convection in a gas near the gas–liquid critical point. Phys. Rev. Lett. 83, 3641–3644.CrossRefGoogle Scholar
Belmonte, A. & Libchaber, A. 1996 Thermal signature of plumes in turbulent convection: the skewness of the derivative. Phys. Rev. E 53, 4893–4898.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1993 Boundary layer length scales in thermal turbulence. Phys. Rev. Lett. 70, 4067–4070.Google Scholar
Belmonte, A., Tilgner, A. & Libchaber, A. 1994 Temperature and velocity boundary layers in turbulent convection. Phys. Rev. E 50, 269–279.Google Scholar
Brown, E. & Ahlers, G. 2006 Rotations and cessations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 568, 351–386.Google Scholar
Castaing, B., Gunaratne, G., Heslot, F., Kadanoff, L., Libchaber, A., Thomae, S., Wu, X.-Z., Zaleski, S. & Zanetti, G. 1989 Scaling of hard thermal turbulence in Rayleigh–Bénard convection. J. Fluid Mech. 204, 1–30.Google Scholar
Chavanne, X., Chilla, F., Castaing, B., Hebral, B., Chabaud, B. & Chaussy, J. 1997 Observation of the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 79, 3648–3651.Google Scholar
Chavanne, X., Chillà, F., Chabaud, B., Castaing, B. & Hébral, B. 2001 Turbulent Rayleigh–Bénard convection in gaseous and liquid He. Phys. Fluids 13, 1300–1320.Google Scholar
Chillá, F., Ciliberto, S., Innocenti, C. & Pampaloni, E. 1993 Boundary layer and scaling properties in turbulent thermal convection. Il Nuovo Cimento D 15, 1229–1249.Google Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.Google Scholar
Ching, E. S. C. 1997 Heat flux and shear rate in turbulent convection. Phys. Rev. E 55, 1189–1192.CrossRefGoogle Scholar
Dubrulle, B. 2001 Logarithmic corrections to scaling in turbulent thermal convection. Eur. Phys. J. B 21, 295–304.Google Scholar
Dubrulle, B. 2002 Scaling in large Prandtl number burbulent thermal convection. Eur. Phys. J. B 28, 361.Google Scholar
Emran, M. S. & Schumacher, J. 2008 Fine-scale statistics of temperature and its derivatives in convective turbulence. J. Fluid Mech. 611, 13–34.Google Scholar
Fernandes, R. L. J. & Adrian, R. J. 2002 Scaling of velocity and temperature fluctuations in turbulent thermal convection. Exp. Therm. Fluid Sci. 26, 355–360.Google Scholar
Funfschilling, D., Brown, E., Nikolaenko, A. & Ahlers, G. 2005 Heat transport by turbulent Rayleigh–Bénard convection in cylindrical samples with aspect ratio one and larger. J. Fluid Mech. 536, 145–154.Google Scholar
Glazier, J. A., Segawa, T., Naert, A. & Sano, M. 1999 Evidence against ultrahard thermal turbulence at very high Rayleigh numbers. Nature 398, 307–310.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 1993 Characteristic scale in Rayleigh–Bénard-convection. Phys. Rev. A 173, 58–62.Google Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.Google Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86, 3316–3319.CrossRefGoogle ScholarPubMed
Grossmann, S. & Lohse, D. 2004 Fluctuations in turbulent Rayleigh–Bénard convection: the role of plumes. Phys. Fluids 16, 4462–4472.Google Scholar
Grossmann, S. & Lohse, D. 2011 Multiple scaling in the ultimate regime of thermal convection. Phys. Fluids 23, 045108.Google Scholar
He, X.-Z., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate regime in Rayleigh–Bénard convection. Phys. Rev. Lett. 108, 024502.Google Scholar
He, X.-Z. & Tong, P. 2009 Measurements of the thermal dissipation field in turbulent Rayleigh–Bénard convection. Phys. Rev. E 79, 026306.Google Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65, 066306.Google Scholar
Li, L., Shi, N., du Puits, R., Resagk, C., Schumacher, J. & Thess, A. 2012 Boundary layer analysis in turbulent Rayleigh–Bénard convection in air: experiment versus simulation. Phys. Rev. E 86, 026315.Google Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Lui, S.-L. & Xia, K.-Q. 1998 Spatial structure of the thermal boundary layer in turbulent convection. Phys. Rev. E 57, 5494–5503.Google Scholar
Malkus, M. V. R. 1951 The heat transport and spectrum of thermal turbulence. Proc. R. Soc. Lond. A 225, 196–212.Google Scholar
Maystrenko, A., Resagk, C. & Thess, A. 2007 Structure of the thermal boundary layer for turbulent Rayleigh–Bénard convection of air in a long rectangular enclosure. Phys. Rev. E 75, 066303.Google Scholar
Naert, A., Segawa, T. & Sano, M. 1997 High-Reynolds-number thermal turbulence in mercury. Phys. Rev. E 56, R1302.Google Scholar
Niemela, J. J., Skrbek, L., Sreenivasan, K. R. & Donnelly, R. J. 2000 Turbulent convection at very high Rayleigh numbers. Nature 404, 837–840.CrossRefGoogle ScholarPubMed
Niemela, J. J. & Sreenivasan, K. R. 2003 Rayleigh-number evolution of large-scale coherent motion in turbulent convection. Europhys. Lett. 62, 829.Google Scholar
Niemela, J. J. & Sreenivasan, K. R. 2006 Turbulent convection at high Rayleigh numbers and aspect ratio 4. J. Fluid Mech. 557, 411–422.Google Scholar
Pohlhausen, E. 1921 Wärmetausch zwischen festen Körpern und Flüssigkeiten mit kleiner Reibund und kleiner Wärmeleitung. Z. Angew. Math. Mech. 1, 115.Google Scholar
Prandtl, L. 1932 Meteorologische anwendungen der stroemungslehre. Beitr. Phys. Atmos. 19, 188–202.Google Scholar
Priestley, C. H. B. 1959 Turbulent Transfer in the Lower Atmosphere. University of Chicago Press.Google Scholar
Procaccia, I., Ching, E. S. C., Constantin, P., Kadanoff, L. P., Libchaber, A. & Xu, X.-Z. 1991 Transitions in convective turbulence: the role of thermal plumes. Phys. Rev. A 44, 8091–8102.Google Scholar
du Puits, R., Resagk, C. & Thess, A. 2007a Mean velocity profile in confined turbulent convection. Phys. Rev. Lett. 99, 234504.Google Scholar
du Puits, R., Resagk, C., Tilgner, A., Busse, F. H. & Thess, A. 2007b Structure of the thermal boundary layer in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 572, 231–254.Google Scholar
Roche, P.-E., Castaing, B., Chabaud, B. & Hébral, B. 2002 Prandtl and Rayleigh numbers dependences in Rayleigh–Bénard convection. Europhys. Lett. 58, 693.CrossRefGoogle Scholar
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12, 085014.Google Scholar
Scheel, J. D., Kim, E. & White, K. R. 2012 Thermal and viscous boundary layers in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 711, 281–305.Google Scholar
Shang, X.-D., Tong, P. & Xia, K.-Q. 2008 Scaling of the local convective heat flux in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 100, 244503.Google Scholar
Shi, N., Emran, M. S. & Schumacher, J. 2012 Boundary layer structure in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 706, 5–33.Google Scholar
Shishkina, O. & Thess, A. 2009 Mean temperature profiles in turbulent Rayleigh–Bénard convection of water. J. Fluid Mech. 633, 449–460.CrossRefGoogle Scholar
Shraiman, B. I. & Siggia, E. D. 1990 Heat transport in high-Rayleigh-number convection. Phys. Rev. A 42, 3650.Google Scholar
Stevens, R. J. A. M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85, 027301.Google Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.Google Scholar
Sun, C., Ren, L.-Y., Song, H. & Xia, K.-Q. 2005 Heat transport by turbulent Rayleigh–Bénard convection in 1 m diameter cylindrical cells of widely varying aspect ratio. J. Fluid Mech. 542, 165–174.Google Scholar
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72, 067302.Google Scholar
Sun, C. & Xia, K.-Q. 2007 Multi-point local temperature measurements inside the conducting plates in turbulent thermal convection. J. Fluid Mech. 570, 479–489.Google Scholar
Tennekes, H. & Lumley, J. L. 1972 A First Course in Turbulence. MIT.Google Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47, R2253.Google Scholar
Verzicco, R. 2012 Boundary layer structure in confined turbulent thermal convection. J. Fluid Mech. 706, 1–4.Google Scholar
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.Google Scholar
Verzicco, R. & Sreenivasan, K. R. 2008 A comparison of turbulent thermal convection between conditions of constant temperature and constant heat flux. J. Fluid Mech. 595, 203–219.Google Scholar
Wagner, S., Shishkina, O. & Wagner, C. 2012 Boundary layers and wind in cylindrical Rayleigh–Bénard cells. J. Fluid Mech. 697, 336–366.Google Scholar
Wang, J. & Xia, K.-Q. 2003 Spatial variations of the mean and statistical quantities in the thermal boundary layers of turbulent convection. Eur. Phys. J. B 32, 127–136.Google Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73, 056312.Google Scholar
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102, 044503.Google Scholar
Xia, K.-Q., Lam, S. & Zhou, S.-Q. 2002 Heat-flux measurement in high-Prandtl-number turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 88, 064501.Google Scholar
Xia, K.-Q., Sun, C. & Zhou, S.-Q. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68, 066303.Google Scholar
Zhou, Q., Li, C.-M., Lu, Z.-M. & Liu, Y.-L. 2011a Experimental investigation of longitudinal space–time correlations of the velocity field in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 683, 94–111.CrossRefGoogle Scholar
Zhou, Q., Liu, B.-F., Li, C.-M. & Zhong, B.-C. 2012 Aspect ratio dependence of heat transport by turbulent Rayleigh–Bénard convection in rectangular cells. J. Fluid Mech. 710, 260–276.Google Scholar
Zhou, Q., Stevens, R. J. A. M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl–Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, Q., Sugiyama, K., Stevens, R. J. A. M., Grossmann, S., Lohse, D. & Xia, K.-Q. 2011b Horizontal structures of velocity and temperature boundary layers in two-dimensional numerical turbulent Rayleigh–Bénard convection. Phys. Fluids 23, 125104.Google Scholar
Zhou, Q., Sun, C. & Xia, K.-Q. 2007a Morphological evolution of thermal plumes in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 98, 074501.CrossRefGoogle ScholarPubMed
Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2007b Measured oscillations of the velocity and temperature fields in turbulent Rayleigh–Bénard convection in a rectangular cell. Phys. Rev. E 76, 036301.Google Scholar
Zhou, Q., Sun, C. & Xia, K.-Q. 2008 Experimental investigation of homogeneity, isotropy and circulation of the velocity field in buoyancy-driven turbulence. J. Fluid Mech. 598, 361–372.Google Scholar
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.Google Scholar
Zhou, Q. & Xia, K.-Q. 2008 Comparative experimental study of local mixing of active and passive scalars in turbulent thermal convection. Phys. Rev. E 77, 056301.Google Scholar
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104, 104301.Google Scholar
Zhou, S.-Q. & Xia, K.-Q. 2001 Scaling properties of the temperature field in convective turbulence. Phys. Rev. Lett. 87, 064501.Google Scholar
Zhou, S.-Q. & Xia, K.-Q. 2002 Plume statistics in thermal turbulence: mixing of an active scalar. Phys. Rev. Lett. 89, 184502.Google Scholar