Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-30T22:00:51.477Z Has data issue: false hasContentIssue false
  • English
  • Français

Thermocapillary flow between longitudinally grooved superhydrophobic surfaces

Published online by Cambridge University Press:  21 September 2018

Ehud Yariv
Ehud Yariv*
Affiliation:
Department of Mathematics, Technion – Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: udi@technion.ac.il
Get access Rights & Permissions [Opens in a new window]

Abstract

A common realisation of superhydrophobic surfaces is based on a periodically grooved solid substrate, with air bubbles trapped in a Cassie state within the grooves. Following Baier, Steffes & Hardt (Phys. Rev. E, vol. 82 (3), 2010, 037301) we consider the thermocapillary flow of a liquid bounded between two such surfaces, driven by a macroscopic temperature gradient. Assuming zero protrusion angle of the free menisci, the periodic geometry is described by two parameters, namely the ratio $\unicode[STIX]{x1D6EC}$ of the groove-array period to the channel depth and the gas fraction 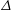$\unicode[STIX]{x1D6E5}$ of the surface. The flow and heat transport depend upon both these parameters, as well as the Marangoni number $Ma$, which quantifies the relative magnitudes of advection and conduction. This paper is concerned with the longitudinal problem, where the temperature gradient is applied along the grooves. The temperature within the highly conducting solid substrate varies linearly with distance and may be regarded as prescribed. For any non-zero value of $Ma$, however, advection necessitates the formation of an excess temperature profile in the liquid domain, above and beyond that linearly varying distribution. The associated Marangoni forces, in turn, imply the formation of flow in the cross-sectional plane. The nonlinearly coupled problem governing the excess temperature and cross-sectional flow is independent of the longitudinal flow. Conversely, the latter satisfies an independent problem in the Stokes limit, and accordingly possesses the standard thermocapillary scaling. A simple transformation reveals a linkage between the longitudinal velocity in the present problem and that in the comparable pressure-driven flow. In studying the coupled problems governing the excess temperature and cross-sectional velocity components, we focus upon deep channels, where 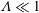$\unicode[STIX]{x1D6EC}\ll 1$. Towards this end, we employ matched asymptotic expansions, with two 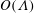$O(\unicode[STIX]{x1D6EC})$-deep inner regions adjacent to the surfaces and an outer region in the remaining fluid domain. The small-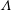$\unicode[STIX]{x1D6EC}$ limit is compatible with two possible scalings of 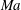$Ma$, the first where it is 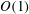$O(1)$ and the second where it is 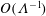$O(\unicode[STIX]{x1D6EC}^{-1})$. In the first scaling, the excess temperature in the outer region is driven by a balance between longitudinal advection and conduction perpendicular to the bounding surfaces. In the inner region, the excess temperature is governed by pure conduction; the cross-sectional flow it animates, which possesses the thermocapillary scaling, is linear in 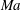$Ma$. In the second scaling, the cross-sectional velocity becomes 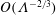$O(\unicode[STIX]{x1D6EC}^{-2/3})$ large relative to the thermocapillary scaling; a boundary layer, of 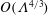$O(\unicode[STIX]{x1D6EC}^{4/3})$ dimensionless width, is formed within the inner region. In that layer the excess temperature is governed by a dominant balance between conduction perpendicular to the surface and cross-sectional advection. The dependence upon 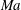$Ma$ is inherently nonlinear.

JFM classification

Low-Reynolds-number flows: Low-Reynolds-number flows Convection: Marangoni convection
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 855 , 25 November 2018 , pp. 574 - 594
Check for updates
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Baier, T., Steffes, C. & Hardt, S. 2010 Thermocapillary flow on superhydrophobic surfaces. Phys. Rev. E 82 (3), 037301.Google Scholar
Balasubramaniam, R. & Subramaniam, R. S. 1996 Thermocapillary bubble migration – thermal boundary layers for large Marangoni numbers. Intl J. Multiphase Flow 22 (3), 593–612.Google Scholar
Balasubramaniam, R. & Subramanian, R. S. 2000 The migration of a drop in a uniform temperature gradient at large Marangoni numbers. Phys. Fluids 12, 733–743.Google Scholar
Batchelor, G. K. 1956 On steady laminar flow with closed streamlines at large Reynolds number. J. Fluid Mech. 1 (2), 177–190.Google Scholar
Bocquet, L. & Lauga, E. 2011 A smooth future? Nature 10 (5), 334–337.Google Scholar
Cottin-Bizonne, C., Barentin, C., Charlaix, É., Bocquet, L. & Barrat, J.-L. 2004 Dynamics of simple liquids at heterogeneous surfaces: molecular-dynamics simulations and hydrodynamic description. Eur. Phys. J. E 15 (4), 427–438.Google Scholar
Cottin-Bizonne, C., Barrat, J.-L., Bocquet, L. & Charlaix, E. 2003 Low-friction flows of liquid at nanopatterned interfaces. Nat. Mater. 2 (4), 238–240.Google Scholar
Crowdy, D. G. 2011 Frictional slip lengths for unidirectional superhydrophobic grooved surfaces. Phys. Fluids 23 (7), 072001.Google Scholar
Crowdy, D. G. 2013 Surfactant-induced stagnant zones in the Jeong–Moffatt free surface Stokes flow problem. Phys. Fluids 25 (9), 092104.Google Scholar
Crowdy, D. G. 2017 Slip length for transverse shear flow over a periodic array of weakly curved menisci. Phys. Fluids 29 (9), 091702.Google Scholar
Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
Hinch, E. J. 1991 Perturbation Methods. Cambridge University Press.Google Scholar
Hodes, M., Kirk, T. L., Karamanis, G. & MacLachlan, S. 2017 Effect of thermocapillary stress on slip length for a channel textured with parallel ridges. J. Fluid Mech. 814, 301–324.Google Scholar
Kirk, T. L., Hodes, M. & Papageorgiou, D. T. 2017 Nusselt numbers for Poiseuille flow over isoflux parallel ridges accounting for meniscus curvature. J. Fluid Mech. 811, 315–349.Google Scholar
Lauga, E. & Stone, H. A. 2003 Effective slip in pressure-driven Stokes flow. J. Fluid Mech. 489, 55–77.Google Scholar
Lee, C., Choi, C.-H. & Kim, C.-J. 2016 Superhydrophobic drag reduction in laminar flows: a critical review. Exp. Fluids 57 (12), 1–20.Google Scholar
Marshall, J. S. 2017 Exact formulae for the effective slip length of a symmetric superhydrophobic channel with flat or weakly curved menisci. SIAM J. Appl. Maths 77 (5), 1606–1630.Google Scholar
Pan, Y.-F. & Acrivos, A. 1968 Heat transfer at high Péclet number in regions of closed streamlines. Intl J. Heat Mass Transfer 11 (3), 439–444.Google Scholar
Philip, J. R. 1972 Flows satisfying mixed no-slip and no-shear conditions. Z. Angew. Math. Phys. 23 (3), 353–372.Google Scholar
Quéré, D. 2005 Non-sticking drops. Rep. Prog. Phys. 68 (11), 2495–2532.Google Scholar
Quéré, D. 2008 Wetting and roughness. Annu. Rev. Mater. Res. 38 (1), 71–99.Google Scholar
Rothstein, J. P. 2010 Slip on superhydrophobic surfaces. Annu. Rev. Fluid Mech. 42 (1), 89–109.Google Scholar
Sbragaglia, M. & Prosperetti, A. 2007 A note on the effective slip properties for microchannel flows with ultrahydrophobic surfaces. Phys. Fluids 19 (4), 043603.Google Scholar
Schnitzer, O. & Yariv, E. 2017 Longitudinal pressure-driven flows between superhydrophobic grooved surfaces: large effective slip in the narrow-channel limit. Phys. Rev. Fluids 2 (7), 072101.Google Scholar
Sen, A. K. & Davis, S. H. 1982 Steady thermocapillary flows in two-dimensional slots. J. Fluid Mech. 121, 163–186.Google Scholar
Subramanian, R. S. 1981 Slow migration of a gas bubble in a thermal gradient. AIChE J. 27, 646–654.Google Scholar
Subramanian, R. S. & Balasubramaniam, R. 2001 The Motion of Bubbles and Drops in Reduced Gravity. Cambridge University Press.Google Scholar
Teo, C. J. & Khoo, B. C. 2009 Analysis of Stokes flow in microchannels with superhydrophobic surfaces containing a periodic array of micro-grooves. Microfluid. Nanofluid. 7 (3), 353–382.Google Scholar
Yariv, E. 2017 Velocity amplification in pressure-driven flows between superhydrophobic gratings of small solid fraction. Soft Matt. 13, 6287–6292.Google Scholar
Young, N. O., Goldstein, J. S. & Block, M. J. 1959 The motion of bubbles in a vertical temperature gradient. J. Fluid Mech. 6 (3), 350–356.Google Scholar
Zhang, L., Subramanian, R. S. & Balasubramaniam, R. 2001 Motion of a drop in a vertical temperature gradient at small Marangoni number – the critical role of inertia. J. Fluid Mech. 448, 197–211.Google Scholar