Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-13T02:33:14.861Z Has data issue: false hasContentIssue false
  • English
  • Français

Thin-film Rayleigh–Taylor instability in the presence of a deep periodic corrugated wall

Published online by Cambridge University Press:  23 November 2021

B. Dinesh Open the ORCID record for B. Dinesh [Opens in a new window] ,
T. Corbin  and
R. Narayanan
B. Dinesh*
Affiliation:
Department of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA
T. Corbin
Affiliation:
Department of Chemical and Biomolecular Engineering, North Carolina State University, Raleigh, NC 27606, USA
R. Narayanan
Affiliation:
Department of Chemical Engineering, University of Florida, Gainesville, FL 32611, USA
*
†Email address for correspondence: dbhagavatula@ufl.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

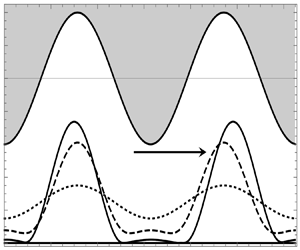
Rayleigh–Taylor instability of a thin liquid film overlying a passive fluid is examined when the film is attached to a periodic wavy deep corrugated wall. A reduced-order long-wave model shows that the wavy wall enhances the instability toward rupture when the interface pattern is sub-harmonic to the wall pattern. An expression that approximates the growth constant of instability is obtained for any value of wall amplitude for the special case when the wall consists of two full waves and the interface consists of a full wave. Nonlinear computations of the interface evolution show that sliding is arrested by the wavy wall if a single liquid film residing over a passive fluid is considered but not necessarily when a bilayer sandwiched by a top wavy wall and bottom flat wall is considered. In the latter case interface tracking shows that primary and secondary troughs will evolve and subsequently slide along the flat wall due to symmetry-breaking. It is further shown that this sliding motion of the interface can ultimately be arrested by the top wavy wall, depending on the holdup of the fluids. In other words, there exists a critical value of the interface position beyond which the onset of the sliding motion is observed and below which the sliding is always arrested.

JFM classification

Interfacial Flows (free surface): Thin films Interfacial Flows (free surface): Capillary flows
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 931 , 25 January 2022 , R5
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Chandrasekhar, S. 1961 Hydrodynamic and Hydromagnetic Stability. Clarendon.Google Scholar
Dietze, G.F., Picardo, J.R. & Narayanan, R. 2018 Sliding instability of draining fluid films. J. Fluid Mech. 857, 111–141.CrossRefGoogle Scholar
Dietze, G.F. & Ruyer-Quil, C. 2015 Films in narrow tubes. J. Fluid Mech. 762, 68–109.CrossRefGoogle Scholar
Glasner, K.B. 2007 The dynamics of pendant droplets on a one-dimensional surface. Phys. Fluids 19 (10), 102104.CrossRefGoogle Scholar
Hesthaven, J.S., Gottlieb, S. & Gottlieb, D. 2007 Spectral Methods for Time-Dependent Problems. Cambridge University Press.CrossRefGoogle Scholar
Kalliadasis, S., Ruyer-Quil, C., Scheid, B. & Velarde, M.G. 2011 Falling Liquid Films. Springer Science & Business Media.Google Scholar
Kumar, K. & Tuckerman, L.S. 1994 Parametric instability of the interface between two fluids. J. Fluid Mech. 279, 49–68.CrossRefGoogle Scholar
Labrosse, G. 2011 Méthodes Spectrales: Méthodes Locales, Méthodes Globales, Problèmes d'Helmotz et de Stokes, équations de Navier–Stokes. Ellipses.Google Scholar
Lister, J.R., Morrison, N.F. & Rallison, J.M. 2006 a Sedimentation of a two-dimensional drop towards a rigid horizontal plane. J. Fluid Mech. 552, 345–351.CrossRefGoogle Scholar
Lister, J.R., Rallison, J.M., King, A.A., Cummings, L.J. & Jensen, O.E. 2006 b Capillary drainage of an annular film: the dynamics of collars and lobes. J. Fluid Mech. 552, 311–343.CrossRefGoogle Scholar
Lister, J.R., Rallison, J.M. & Rees, S.J. 2010 The nonlinear dynamics of pendent drops on a thin film coating the underside of a ceiling. J. Fluid Mech. 647, 239–264.CrossRefGoogle Scholar
Luo, D. & Tao, J. 2018 Dripping retardation with corrugated ceiling. Z. Angew. Math. Mech. 39 (8), 1165–1172.CrossRefGoogle Scholar
Nayfeh, A.H. 2011 Introduction to Perturbation Techniques. John Wiley & Sons.Google Scholar
Pillai, D.S. & Narayanan, R. 2018 Nonlinear dynamics of electrostatic faraday instability in thin films. J. Fluid Mech. 855, R4.CrossRefGoogle Scholar
Quéré, D. 1999 Fluid coating on a fiber. Annu. Rev. Fluid Mech. 31 (1), 347–384.CrossRefGoogle Scholar
Sharp, D.H. 1983 Overview of Rayleigh–Taylor instability. Tech. Rep. Los Alamos National Laboratory.Google Scholar
Weinstein, S.J. & Ruschak, K.J. 2004 Coating flows. Annu. Rev. Fluid Mech. 36, 29–53.CrossRefGoogle Scholar
Yiantsios, S.G. & Higgins, B.G. 1989 Rayleigh–Taylor instability in thin viscous films. Phys. Fluids A 1 (9), 1484–1501.CrossRefGoogle Scholar

Dinesh et al. supplementary movie 1

Sliding motion of a thin layer of water suspended from a flat wall due to Rayleigh-Taylor instability
Download Dinesh et al. supplementary movie 1(Video)
Video 78.2 MB

Dinesh et al. supplementary movie 2

Arresting sliding motion of the free surface of a thin layer of water suspended from a wavy wall. Here the initial perturbation is out of phase with the shape of the wavy wall

Download Dinesh et al. supplementary movie 2(Video)
Video 6.8 MB

Dinesh et al. supplementary movie 3

Arresting sliding motion of the free surface of a thin layer of water suspended from a wavy wall. Here the initial perturbation is in phase with the shape of the wavy wall

Download Dinesh et al. supplementary movie 3(Video)
Video 3 MB

Dinesh et al. supplementary movie 4

Sliding of the interface between silicone oil (1.5 cSt bottom layer) and water (top layer) as the interface approaches the wall. Here the sliding motion is arrested due to the presence of a wavy wall

Download Dinesh et al. supplementary movie 4(Video)
Video 8.7 MB

Dinesh et al. supplementary movie 5

Sliding of the interface between silicone oil (1.5 cSt bottom layer) and water (top layer) as the interface approaches the wall. The interface continues to slide on the flat wall located at z=1

Download Dinesh et al. supplementary movie 5(Video)
Video 11.9 MB
Supplementary material: PDF

Dinesh et al. supplementary material

Supplementary data

Download Dinesh et al. supplementary material(PDF)
PDF 670.6 KB