1. Introduction
Thin-film approximations have been enormously successful tools for understanding a wide range of flows. The slender geometry of a flow domain can be exploited not only to highlight dominant physical processes, but also to simplify the flow's mathematical description very substantially. The celebrated pioneers of this approach used physical insight to identify approximations describing, for example, high pressures generated by viscous effects in lubricating bearings (Reynolds Reference Reynolds1886) and the regulation of the thickness of coating flows by viscosity and surface tension (Landau & Levich Reference Landau and Levich1942). In each case, the resulting theory yielded a low-dimensional description of the flow, formulated as an ordinary or partial differential equation describing the film thickness or pressure field, while still accommodating non-trivial nonlinearity.
More systematic approaches to deriving low-dimensional approximations emerged later in the last century with the maturing of asymptotic methods. A small parameter  $\epsilon$, capturing the flow's extreme aspect ratio, is used to rescale the governing equations (and relevant dimensionless parameters), and dimensionless variables are then expanded, normally in algebraic powers of
$\epsilon$, capturing the flow's extreme aspect ratio, is used to rescale the governing equations (and relevant dimensionless parameters), and dimensionless variables are then expanded, normally in algebraic powers of  $\epsilon$. Models of this kind can be grouped broadly into two classes: those describing thin viscous films adjacent to solid surfaces for which the flow is dominated by shear, and ‘free’ films in which stretching and bending deformations (and the associated stresses) are dominant. In the former category Atherton & Homsy (Reference Atherton and Homsy1976), for example, showed how to derive systematically nonlinear evolution equations which can accommodate a variety of physical effects such as weak inertia, surface tension, substrate curvature and gravity; a wealth of discoveries exploiting this approach followed (Craster & Matar Reference Craster and Matar2009). At around the same time, Buckmaster, Nachman & Ting (Reference Buckmaster, Nachman and Ting1975) derived evolution equations for the centreline of a thin sheet of viscous fluid (a ‘viscida’, complementing treatment of the corresponding ‘elastica’ in the framework of solid mechanics), an approach which subsequently found success in industrial applications such as glass blowing (Van De Fliert, Howell & Ockenden Reference Van De Fliert, Howell and Ockenden1995) and in describing fundamental processes such as the buckling (Ribe Reference Ribe2001) and breakup (Eggers & Villermaux Reference Eggers and Villermaux2008) of liquid columns.
$\epsilon$. Models of this kind can be grouped broadly into two classes: those describing thin viscous films adjacent to solid surfaces for which the flow is dominated by shear, and ‘free’ films in which stretching and bending deformations (and the associated stresses) are dominant. In the former category Atherton & Homsy (Reference Atherton and Homsy1976), for example, showed how to derive systematically nonlinear evolution equations which can accommodate a variety of physical effects such as weak inertia, surface tension, substrate curvature and gravity; a wealth of discoveries exploiting this approach followed (Craster & Matar Reference Craster and Matar2009). At around the same time, Buckmaster, Nachman & Ting (Reference Buckmaster, Nachman and Ting1975) derived evolution equations for the centreline of a thin sheet of viscous fluid (a ‘viscida’, complementing treatment of the corresponding ‘elastica’ in the framework of solid mechanics), an approach which subsequently found success in industrial applications such as glass blowing (Van De Fliert, Howell & Ockenden Reference Van De Fliert, Howell and Ockenden1995) and in describing fundamental processes such as the buckling (Ribe Reference Ribe2001) and breakup (Eggers & Villermaux Reference Eggers and Villermaux2008) of liquid columns.
In contrast, well-grounded theories for thin films or sheets of non-Newtonian liquids have taken longer to develop. The additional physical complexity, such as history dependence (for viscoelastic or thixotropic materials) and fine-grained physical structures (such as internal plugs, wall slip or shear bands for yield-stress materials), described by a diverse set of constitutive models, have often prompted ad hoc approximations at the expense of more systematic approaches. Hewitt & Balmforth (Reference Hewitt and Balmforth2021) take the field forward by developing new asymptotic descriptions for thin sheets of viscoelastic and elasto-viscoplastic material, and solving a set of canonical problems that demonstrate how these materials show a spectrum of fluid-like and solid-like properties.
2. Overview
Hewitt & Balmforth (Reference Hewitt and Balmforth2021) focus initially on the motion of a two-dimensional sheet of incompressible material, ignoring the effects of inertia and surface tension, and adopting the linear constitutive Oldroyd-B model of viscoelasticity. After formulating governing equations in an intrinsic coordinate system (using arc-length  $s$ along the sheet centreline and the direction normal to this), a scaling is identified that is appropriate to the slender domain. Careful analysis reveals a regime in which axial stress dominates shear stresses and, crucially, bending deformations dominate stretching, with negligible change of sheet thickness. Within this framework, the sheet can curve over distances comparable to its length, with its shape captured compactly at time
$s$ along the sheet centreline and the direction normal to this), a scaling is identified that is appropriate to the slender domain. Careful analysis reveals a regime in which axial stress dominates shear stresses and, crucially, bending deformations dominate stretching, with negligible change of sheet thickness. Within this framework, the sheet can curve over distances comparable to its length, with its shape captured compactly at time  $t$ by the centreline curvature
$t$ by the centreline curvature  $\kappa (s,t)$. After integrating across the width of the sheet, the model reduces to that resembling elastic (Euler–Bernoulli) beam theory, but with a modified constitutive law (regulated by three independent parameters – two viscosities and an elastic modulus) that relates bending moment (and its time derivative) to time derivatives of
$\kappa (s,t)$. After integrating across the width of the sheet, the model reduces to that resembling elastic (Euler–Bernoulli) beam theory, but with a modified constitutive law (regulated by three independent parameters – two viscosities and an elastic modulus) that relates bending moment (and its time derivative) to time derivatives of  $\kappa$. This neatly mirrors one-dimensional models for viscoelasticity, incorporating the Maxwell formulation (allowing stress relaxation), the Kelvin formulation (allowing the buildup of elastic stress) and their combination, generalising previous treatments for Newtonian liquid sheets by Buckmaster et al. (Reference Buckmaster, Nachman and Ting1975), Ribe (Reference Ribe2001) and others. Axial tension plays a role as a Lagrange multiplier, enforcing effective inextensibility.
$\kappa$. This neatly mirrors one-dimensional models for viscoelasticity, incorporating the Maxwell formulation (allowing stress relaxation), the Kelvin formulation (allowing the buildup of elastic stress) and their combination, generalising previous treatments for Newtonian liquid sheets by Buckmaster et al. (Reference Buckmaster, Nachman and Ting1975), Ribe (Reference Ribe2001) and others. Axial tension plays a role as a Lagrange multiplier, enforcing effective inextensibility.
The model is then used to address a set of representative problems, notably a cantilever (clamped at one end, with the other free to sag under gravity), allowing creep to develop at long times (although the model does not incorporate subsequent stretching). Buckling is induced by bringing the two ends of the clamped beam together, with creep promoting instability. A third example involves ‘snap through’, induced by rotation of the ends of a beam in a buckled configuration, allowing it to jump towards another buckled state, with the rate of transition regulated by viscous dissipation. Sufficient viscosity suppresses the snap through altogether, although some hysteresis remains.
A variant of the model is then presented in which there is a balance between stretching and curvature: small lateral deflections induce stretching that in turn induces a spatially uniform axial tension in the sheet. The problem is formulated as a high-order partial differential equation for the lateral beam displacement, coupled to an evolution equation for the tension that is a nonlinear function of the displacement. Solutions are illustrated for the viscous catenary (a sheet clamped at either end, held initially horizontally in a vertical gravitational field). When the solvent viscosity  $\eta _s$ is small, and the polymer viscosity
$\eta _s$ is small, and the polymer viscosity  $\eta$ (regulating the relaxation rate of elastic stresses) is large, initial deflection of the catenary is controlled by viscous bending at a rate determined by
$\eta$ (regulating the relaxation rate of elastic stresses) is large, initial deflection of the catenary is controlled by viscous bending at a rate determined by  $\eta _s$. Elastic stresses then accumulate and the catenary lingers close to an elastic equilibrium; finally over longer times, the catenary starts to creep at a rate regulated by
$\eta _s$. Elastic stresses then accumulate and the catenary lingers close to an elastic equilibrium; finally over longer times, the catenary starts to creep at a rate regulated by  $\eta$, with bending and then stretching dominating the motion.
$\eta$, with bending and then stretching dominating the motion.
Strong nonlinearity is added to the constitutive law in the final section of the study, through the introduction of a yield stress above which stresses can relax through irreversible plastic deformation. Prior studies in this area have offered divergent predictions, because of a focus on different parameter regimes but also as a result of different modelling approaches. Kamrin & Mahadevan (Reference Kamrin and Mahadevan2012) developed an approximate theory for a slender Bingham–Norton (elasto-viscoplastic) catenary based on an assumption that stress varies linearly across the cross-section; their model was successful in identifying regions of yield in three-dimensional finite-element simulations. In a study of a ribbon being curled by passing it under high axial tension over a sharp blade, Prior etal. (Reference Prior, Moussou, Chakrabarti, Jensen and Juel2016) (developing an elasto-viscoplastic model that assumed instead a linear strain profile across the cross-section) predicted that internal yield surfaces emerge that are almost parallel to the centreline of the ribbon, so that plastic deformations along one edge of the ribbon lead to a permanent curl, capturing key features of experimental measurements. Neither of these approaches, however, involved systematic asymptotic reduction of a higher-dimensional model. First steps in that direction had been taken by Balmforth & Hewitt (Reference Balmforth and Hewitt2013), who investigated slender Herschel–Bulkley (purely viscoplastic) sheets and threads (using toothpaste extruded from its tube as motivation), proposing that yielded (flowing) regions are separated from unyielded (plug) regions by surfaces orthogonal to the axis of the thread.
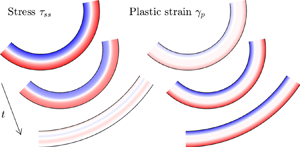
Hewitt & Balmforth (Reference Hewitt and Balmforth2021) explore the ground between these studies by adopting the Bingham–Maxwell elasto-viscoplastic model (in a properly invariant formulation due to Saramito Reference Saramito2007) again considering a regime in which axial tension is weak enough to avoid significant stretching. They derive a new reduced constitutive model relating bending moment to curvature, modified by the first moment of plastic strain across the cross-section of the sheet. For a sheet that bends without stretching significantly, stresses are largest near the lateral surfaces of the sheet, being tensile at the outer surface of the bend and compressive at the inner, causing yielded regions to propagate inwards toward the sheet centreline. This behaviour is illustrated for a cantilever (undergoing small deflections for which the bending moment is known), with the migration of the yield surfaces through the material being coupled to the evolution of bending moment and curvature. The model illustrates elegantly how the rate and degree of droop of the cantilever is regulated by yield stress.
3. Future
Thin-sheet flows of viscoelastic and viscoplastic materials appear in a variety of applications, from the domestic environment (such as curling hair or ribbons) to the natural world (growing plant cell walls in Boudon et al. (Reference Boudon, Chopard, Ali, Gilles, Hamant, Boudaoud, Traas and Godin2015) or flowing lung airway mucus in Lai et al. (Reference Lai, Wang, Wirtz and Hanes2009), for example). The highly idealised constitutive models mentioned so far will likely over-simplify the complex rheology of many natural or manufactured materials. Beyond identification of appropriate parameter values, and the introduction of material nonlinearities, lie challenging questions over the representation of yielding behaviour in materials with complex microstructure (Balmforth, Frigaard & Ovarlez Reference Balmforth, Frigaard and Ovarlez2014; Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017), which new generations of constitutive models are starting to address (Dimitriou & McKinley Reference Dimitriou and McKinley2019). Nevertheless, Hewitt & Balmforth (Reference Hewitt and Balmforth2021) make clear predictions that can be tested experimentally, and the theoretical framework they have developed will support analysis of more complex constitutive models and a wider range of deformations.



1. Introduction
Thin-film approximations have been enormously successful tools for understanding a wide range of flows. The slender geometry of a flow domain can be exploited not only to highlight dominant physical processes, but also to simplify the flow's mathematical description very substantially. The celebrated pioneers of this approach used physical insight to identify approximations describing, for example, high pressures generated by viscous effects in lubricating bearings (Reynolds Reference Reynolds1886) and the regulation of the thickness of coating flows by viscosity and surface tension (Landau & Levich Reference Landau and Levich1942). In each case, the resulting theory yielded a low-dimensional description of the flow, formulated as an ordinary or partial differential equation describing the film thickness or pressure field, while still accommodating non-trivial nonlinearity.
More systematic approaches to deriving low-dimensional approximations emerged later in the last century with the maturing of asymptotic methods. A small parameter $\epsilon$, capturing the flow's extreme aspect ratio, is used to rescale the governing equations (and relevant dimensionless parameters), and dimensionless variables are then expanded, normally in algebraic powers of
$\epsilon$, capturing the flow's extreme aspect ratio, is used to rescale the governing equations (and relevant dimensionless parameters), and dimensionless variables are then expanded, normally in algebraic powers of  $\epsilon$. Models of this kind can be grouped broadly into two classes: those describing thin viscous films adjacent to solid surfaces for which the flow is dominated by shear, and ‘free’ films in which stretching and bending deformations (and the associated stresses) are dominant. In the former category Atherton & Homsy (Reference Atherton and Homsy1976), for example, showed how to derive systematically nonlinear evolution equations which can accommodate a variety of physical effects such as weak inertia, surface tension, substrate curvature and gravity; a wealth of discoveries exploiting this approach followed (Craster & Matar Reference Craster and Matar2009). At around the same time, Buckmaster, Nachman & Ting (Reference Buckmaster, Nachman and Ting1975) derived evolution equations for the centreline of a thin sheet of viscous fluid (a ‘viscida’, complementing treatment of the corresponding ‘elastica’ in the framework of solid mechanics), an approach which subsequently found success in industrial applications such as glass blowing (Van De Fliert, Howell & Ockenden Reference Van De Fliert, Howell and Ockenden1995) and in describing fundamental processes such as the buckling (Ribe Reference Ribe2001) and breakup (Eggers & Villermaux Reference Eggers and Villermaux2008) of liquid columns.
$\epsilon$. Models of this kind can be grouped broadly into two classes: those describing thin viscous films adjacent to solid surfaces for which the flow is dominated by shear, and ‘free’ films in which stretching and bending deformations (and the associated stresses) are dominant. In the former category Atherton & Homsy (Reference Atherton and Homsy1976), for example, showed how to derive systematically nonlinear evolution equations which can accommodate a variety of physical effects such as weak inertia, surface tension, substrate curvature and gravity; a wealth of discoveries exploiting this approach followed (Craster & Matar Reference Craster and Matar2009). At around the same time, Buckmaster, Nachman & Ting (Reference Buckmaster, Nachman and Ting1975) derived evolution equations for the centreline of a thin sheet of viscous fluid (a ‘viscida’, complementing treatment of the corresponding ‘elastica’ in the framework of solid mechanics), an approach which subsequently found success in industrial applications such as glass blowing (Van De Fliert, Howell & Ockenden Reference Van De Fliert, Howell and Ockenden1995) and in describing fundamental processes such as the buckling (Ribe Reference Ribe2001) and breakup (Eggers & Villermaux Reference Eggers and Villermaux2008) of liquid columns.
In contrast, well-grounded theories for thin films or sheets of non-Newtonian liquids have taken longer to develop. The additional physical complexity, such as history dependence (for viscoelastic or thixotropic materials) and fine-grained physical structures (such as internal plugs, wall slip or shear bands for yield-stress materials), described by a diverse set of constitutive models, have often prompted ad hoc approximations at the expense of more systematic approaches. Hewitt & Balmforth (Reference Hewitt and Balmforth2021) take the field forward by developing new asymptotic descriptions for thin sheets of viscoelastic and elasto-viscoplastic material, and solving a set of canonical problems that demonstrate how these materials show a spectrum of fluid-like and solid-like properties.
2. Overview
Hewitt & Balmforth (Reference Hewitt and Balmforth2021) focus initially on the motion of a two-dimensional sheet of incompressible material, ignoring the effects of inertia and surface tension, and adopting the linear constitutive Oldroyd-B model of viscoelasticity. After formulating governing equations in an intrinsic coordinate system (using arc-length $s$ along the sheet centreline and the direction normal to this), a scaling is identified that is appropriate to the slender domain. Careful analysis reveals a regime in which axial stress dominates shear stresses and, crucially, bending deformations dominate stretching, with negligible change of sheet thickness. Within this framework, the sheet can curve over distances comparable to its length, with its shape captured compactly at time
$s$ along the sheet centreline and the direction normal to this), a scaling is identified that is appropriate to the slender domain. Careful analysis reveals a regime in which axial stress dominates shear stresses and, crucially, bending deformations dominate stretching, with negligible change of sheet thickness. Within this framework, the sheet can curve over distances comparable to its length, with its shape captured compactly at time  $t$ by the centreline curvature
$t$ by the centreline curvature  $\kappa (s,t)$. After integrating across the width of the sheet, the model reduces to that resembling elastic (Euler–Bernoulli) beam theory, but with a modified constitutive law (regulated by three independent parameters – two viscosities and an elastic modulus) that relates bending moment (and its time derivative) to time derivatives of
$\kappa (s,t)$. After integrating across the width of the sheet, the model reduces to that resembling elastic (Euler–Bernoulli) beam theory, but with a modified constitutive law (regulated by three independent parameters – two viscosities and an elastic modulus) that relates bending moment (and its time derivative) to time derivatives of  $\kappa$. This neatly mirrors one-dimensional models for viscoelasticity, incorporating the Maxwell formulation (allowing stress relaxation), the Kelvin formulation (allowing the buildup of elastic stress) and their combination, generalising previous treatments for Newtonian liquid sheets by Buckmaster et al. (Reference Buckmaster, Nachman and Ting1975), Ribe (Reference Ribe2001) and others. Axial tension plays a role as a Lagrange multiplier, enforcing effective inextensibility.
$\kappa$. This neatly mirrors one-dimensional models for viscoelasticity, incorporating the Maxwell formulation (allowing stress relaxation), the Kelvin formulation (allowing the buildup of elastic stress) and their combination, generalising previous treatments for Newtonian liquid sheets by Buckmaster et al. (Reference Buckmaster, Nachman and Ting1975), Ribe (Reference Ribe2001) and others. Axial tension plays a role as a Lagrange multiplier, enforcing effective inextensibility.
The model is then used to address a set of representative problems, notably a cantilever (clamped at one end, with the other free to sag under gravity), allowing creep to develop at long times (although the model does not incorporate subsequent stretching). Buckling is induced by bringing the two ends of the clamped beam together, with creep promoting instability. A third example involves ‘snap through’, induced by rotation of the ends of a beam in a buckled configuration, allowing it to jump towards another buckled state, with the rate of transition regulated by viscous dissipation. Sufficient viscosity suppresses the snap through altogether, although some hysteresis remains.
A variant of the model is then presented in which there is a balance between stretching and curvature: small lateral deflections induce stretching that in turn induces a spatially uniform axial tension in the sheet. The problem is formulated as a high-order partial differential equation for the lateral beam displacement, coupled to an evolution equation for the tension that is a nonlinear function of the displacement. Solutions are illustrated for the viscous catenary (a sheet clamped at either end, held initially horizontally in a vertical gravitational field). When the solvent viscosity $\eta _s$ is small, and the polymer viscosity
$\eta _s$ is small, and the polymer viscosity  $\eta$ (regulating the relaxation rate of elastic stresses) is large, initial deflection of the catenary is controlled by viscous bending at a rate determined by
$\eta$ (regulating the relaxation rate of elastic stresses) is large, initial deflection of the catenary is controlled by viscous bending at a rate determined by  $\eta _s$. Elastic stresses then accumulate and the catenary lingers close to an elastic equilibrium; finally over longer times, the catenary starts to creep at a rate regulated by
$\eta _s$. Elastic stresses then accumulate and the catenary lingers close to an elastic equilibrium; finally over longer times, the catenary starts to creep at a rate regulated by  $\eta$, with bending and then stretching dominating the motion.
$\eta$, with bending and then stretching dominating the motion.
Strong nonlinearity is added to the constitutive law in the final section of the study, through the introduction of a yield stress above which stresses can relax through irreversible plastic deformation. Prior studies in this area have offered divergent predictions, because of a focus on different parameter regimes but also as a result of different modelling approaches. Kamrin & Mahadevan (Reference Kamrin and Mahadevan2012) developed an approximate theory for a slender Bingham–Norton (elasto-viscoplastic) catenary based on an assumption that stress varies linearly across the cross-section; their model was successful in identifying regions of yield in three-dimensional finite-element simulations. In a study of a ribbon being curled by passing it under high axial tension over a sharp blade, Prior etal. (Reference Prior, Moussou, Chakrabarti, Jensen and Juel2016) (developing an elasto-viscoplastic model that assumed instead a linear strain profile across the cross-section) predicted that internal yield surfaces emerge that are almost parallel to the centreline of the ribbon, so that plastic deformations along one edge of the ribbon lead to a permanent curl, capturing key features of experimental measurements. Neither of these approaches, however, involved systematic asymptotic reduction of a higher-dimensional model. First steps in that direction had been taken by Balmforth & Hewitt (Reference Balmforth and Hewitt2013), who investigated slender Herschel–Bulkley (purely viscoplastic) sheets and threads (using toothpaste extruded from its tube as motivation), proposing that yielded (flowing) regions are separated from unyielded (plug) regions by surfaces orthogonal to the axis of the thread.
Hewitt & Balmforth (Reference Hewitt and Balmforth2021) explore the ground between these studies by adopting the Bingham–Maxwell elasto-viscoplastic model (in a properly invariant formulation due to Saramito Reference Saramito2007) again considering a regime in which axial tension is weak enough to avoid significant stretching. They derive a new reduced constitutive model relating bending moment to curvature, modified by the first moment of plastic strain across the cross-section of the sheet. For a sheet that bends without stretching significantly, stresses are largest near the lateral surfaces of the sheet, being tensile at the outer surface of the bend and compressive at the inner, causing yielded regions to propagate inwards toward the sheet centreline. This behaviour is illustrated for a cantilever (undergoing small deflections for which the bending moment is known), with the migration of the yield surfaces through the material being coupled to the evolution of bending moment and curvature. The model illustrates elegantly how the rate and degree of droop of the cantilever is regulated by yield stress.
3. Future
Thin-sheet flows of viscoelastic and viscoplastic materials appear in a variety of applications, from the domestic environment (such as curling hair or ribbons) to the natural world (growing plant cell walls in Boudon et al. (Reference Boudon, Chopard, Ali, Gilles, Hamant, Boudaoud, Traas and Godin2015) or flowing lung airway mucus in Lai et al. (Reference Lai, Wang, Wirtz and Hanes2009), for example). The highly idealised constitutive models mentioned so far will likely over-simplify the complex rheology of many natural or manufactured materials. Beyond identification of appropriate parameter values, and the introduction of material nonlinearities, lie challenging questions over the representation of yielding behaviour in materials with complex microstructure (Balmforth, Frigaard & Ovarlez Reference Balmforth, Frigaard and Ovarlez2014; Bonn et al. Reference Bonn, Denn, Berthier, Divoux and Manneville2017), which new generations of constitutive models are starting to address (Dimitriou & McKinley Reference Dimitriou and McKinley2019). Nevertheless, Hewitt & Balmforth (Reference Hewitt and Balmforth2021) make clear predictions that can be tested experimentally, and the theoretical framework they have developed will support analysis of more complex constitutive models and a wider range of deformations.
Declaration of interest
The author reports no conflict of interest.