Article contents
Three-dimensional effects on flag flapping dynamics
Published online by Cambridge University Press: 19 October 2015
Abstract
We examine three-dimensional (3D) effects on the flapping dynamics of a flag, modelled as a thin membrane, in uniform fluid inflow. We consider periodic spanwise variations of length 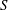 $S$ (ignoring edge effects), so that the 3D effects are characterized by the dimensionless spanwise wavelength
$S$ (ignoring edge effects), so that the 3D effects are characterized by the dimensionless spanwise wavelength 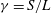 ${\it\gamma}=S/L$, where
${\it\gamma}=S/L$, where 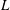 $L$ is the chord length. We perform linear stability analysis (LSA) to show increase in stability with
$L$ is the chord length. We perform linear stability analysis (LSA) to show increase in stability with 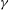 ${\it\gamma}$, with the purely 2D mode being the most unstable. To confirm the LSA and to study nonlinear responses of 3D flapping, we obtain direct numerical simulations, up to Reynolds number 1000 based on
${\it\gamma}$, with the purely 2D mode being the most unstable. To confirm the LSA and to study nonlinear responses of 3D flapping, we obtain direct numerical simulations, up to Reynolds number 1000 based on 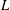 $L$, coupling solvers for the Navier–Stokes equations and that for a thin membrane structure undergoing arbitrarily large displacement. For nonlinear flapping evolution, we identify and characterize the effect of
$L$, coupling solvers for the Navier–Stokes equations and that for a thin membrane structure undergoing arbitrarily large displacement. For nonlinear flapping evolution, we identify and characterize the effect of 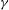 ${\it\gamma}$ on the distinct flag motions and wake vortex structures, corresponding to spanwise standing wave (SW) and travelling wave (TW) modes, in the absence and presence of cross-flow respectively. For both SW and TW, the response is characterized by an initial instability growth phase (I), followed by a nonlinear development phase (II) consisting of multiple unstable 3D modes, and tending, in long time, towards a quasi-steady limit-cycle response (III) dominated by a single (most unstable) mode. Phase I follows closely the predictions of LSA for initial instability and growth rates, with the latter increased for TW due to suppression of restoring forces by the cross-flow. Phase II is characterized by multiple competing flapping modes with energy cascading towards the more unstable mode(s). The wake is characterized by interwoven (SW) and oblique continuous (TW) shed vortices. For phase III, the persistent single dominant mode for SW is the (most unstable) 2D flag displacement with a continuous parallel wake structure; and for TW, the fundamental oblique travelling-wave flag displacement corresponding to the given
${\it\gamma}$ on the distinct flag motions and wake vortex structures, corresponding to spanwise standing wave (SW) and travelling wave (TW) modes, in the absence and presence of cross-flow respectively. For both SW and TW, the response is characterized by an initial instability growth phase (I), followed by a nonlinear development phase (II) consisting of multiple unstable 3D modes, and tending, in long time, towards a quasi-steady limit-cycle response (III) dominated by a single (most unstable) mode. Phase I follows closely the predictions of LSA for initial instability and growth rates, with the latter increased for TW due to suppression of restoring forces by the cross-flow. Phase II is characterized by multiple competing flapping modes with energy cascading towards the more unstable mode(s). The wake is characterized by interwoven (SW) and oblique continuous (TW) shed vortices. For phase III, the persistent single dominant mode for SW is the (most unstable) 2D flag displacement with a continuous parallel wake structure; and for TW, the fundamental oblique travelling-wave flag displacement corresponding to the given 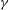 ${\it\gamma}$ with continuous oblique shedding. The transition to phase III occurs slower for greater
${\it\gamma}$ with continuous oblique shedding. The transition to phase III occurs slower for greater 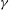 ${\it\gamma}$. For the total forces, drag decreases for both SW and TW with decreasing
${\it\gamma}$. For the total forces, drag decreases for both SW and TW with decreasing 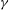 ${\it\gamma}$, while lift is negligible in phase I and II and comparable in magnitude to drag in phase III for any
${\it\gamma}$, while lift is negligible in phase I and II and comparable in magnitude to drag in phase III for any 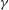 ${\it\gamma}$.
${\it\gamma}$.
JFM classification
- Type
- Papers
- Information
- Copyright
- © 2015 Cambridge University Press
Footnotes
Present address: Applied Physical Sciences Corporation, Groton, CT 06340, USA.
References
- 20
- Cited by



