Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T06:50:47.901Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensional properties of the viscous boundary layer in turbulent Rayleigh–Bénard convection

Published online by Cambridge University Press:  22 August 2022

Fang Xu Open the ORCID record for Fang Xu [Opens in a new window] ,
Lu Zhang Open the ORCID record for Lu Zhang [Opens in a new window]  and
Ke-Qing Xia Open the ORCID record for Ke-Qing Xia [Opens in a new window]
Fang Xu
Affiliation:
Center for Complex Flows and Soft Matter Research, and Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
Lu Zhang*
Affiliation:
Center for Complex Flows and Soft Matter Research, and Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
Ke-Qing Xia*
Affiliation:
Center for Complex Flows and Soft Matter Research, and Department of Mechanics and Aerospace Engineering, Southern University of Science and Technology, Shenzhen 518055, PR China
*
†Email addresses for correspondence: zhangl39@sustech.edu.cn, xiakq@sustech.edu.cn
†Email addresses for correspondence: zhangl39@sustech.edu.cn, xiakq@sustech.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

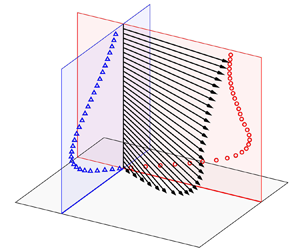
We report an experimental study of the viscous boundary layer (BL) properties of turbulent Rayleigh–Bénard convection in a cylindrical cell. The velocity profile with all three components was measured from the centre of the bottom plate by an integrated home-made particle image velocimetry system. The Rayleigh number $Ra$ varied in the range $1.82 \times 10^8 \le Ra \le 5.26 \times 10^9$ and the Prandtl number $Pr$ was fixed at $Pr = 4.34$. The probability density function of the wall-shear stress indicates that using the velocity component in the mean large-scale circulation (LSC) plane alone may not be sufficient to characterise the viscous BL. Based on a dynamic wall-shear frame, we propose a method to reconstruct the measured full velocity profile which eliminates the effects of complex dynamics of the LSC. Various BL properties including the eddy viscosity are then obtained and analysed. It is found that, in the dynamic wall-shear frame, the eddy viscosity profiles along the centre line of the convection cell at different $Ra$ all collapse on a single master curve described by $\nu _t^d / \nu = 0.81 (z / \delta _u^d) ^{3.10 \pm 0.05}$. The Rayleigh number dependencies of several BL quantities are also determined in the dynamic frame, including the BL thickness $\delta _u^d$ (${\sim } Ra^{-0.21}$), the Reynolds number $Re^d$ (${\sim }Ra^{-0.46}$) and the shear Reynolds number $Re_s^d$ (${\sim } Ra^{0.24}$). Within the experimental uncertainty, these scaling exponents are the same as those obtained in the static laboratory frame. Finally, with the measured full velocity profile, we obtain the energy dissipation rate at the centre of the bottom plate $\varepsilon _{w}$, which is found to follow $\langle \varepsilon _{w} \rangle _t \sim Ra^{1.25}$.

JFM classification

Turbulent Flows: Turbulent convection Convection: Buoyant boundary layers
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 947 , 25 September 2022 , A15
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Ahlers, G. 2022 Aspect ratio dependence of heat transfer in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 128 (8), 084501.CrossRefGoogle Scholar
Ahlers, G., Brown, E. & Nikolaenko, A. 2006 The search for slow transients, and the effect of imperfect vertical alignment, in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 557, 347–367.CrossRefGoogle Scholar
Ahlers, G., Grossmann, S. & Lohse, D. 2009 Heat transfer and large scale dynamics in turbulent Rayleigh–Bénard convection. Rev. Mod. Phys. 81 (2), 503–537.CrossRefGoogle Scholar
Chillà, F. & Schumacher, J. 2012 New perspectives in turbulent Rayleigh–Bénard convection. Eur. Phys. J. E 35, 58.CrossRefGoogle ScholarPubMed
Ching, E.S.C., Leung, H.S., Zwirner, L. & Shishkina, O. 2019 Velocity and thermal boundary layer equations for turbulent Rayleigh–Bénard convection. Phys. Rev. Res. 1 (3), 33037.CrossRefGoogle Scholar
Cioni, S., Ciliberto, S. & Sommeria, J. 1997 Strongly turbulent Rayleigh–Bénard convection in mercury: comparison with results at moderate Prandtl number. J. Fluid Mech. 335, 111–140.CrossRefGoogle Scholar
Funfschilling, D. & Ahlers, G. 2004 Plume motion and large-scale circulation in a cylindrical Rayleigh–Bénard cell. Phys. Rev. Lett. 92 (19), 194502.CrossRefGoogle Scholar
Funfschilling, D., Brown, E. & Ahlers, G. 2008 Torsional oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 607, 119–139.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2000 Scaling in thermal convection: a unifying theory. J. Fluid Mech. 407, 27–56.CrossRefGoogle Scholar
Grossmann, S. & Lohse, D. 2001 Thermal convection for large Prandtl numbers. Phys. Rev. Lett. 86 (15), 3316–3319.CrossRefGoogle ScholarPubMed
He, X., Bodenschatz, E. & Ahlers, G. 2020 Aspect ratio dependence of the ultimate-state transition in turbulent thermal convection. Proc. Natl Acad. Sci. USA 117 (48), 30022–30023.CrossRefGoogle ScholarPubMed
He, X., Funfschilling, D., Nobach, H., Bodenschatz, E. & Ahlers, G. 2012 Transition to the ultimate state of turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 108 (2), 024502.CrossRefGoogle Scholar
Kraichnan, R.H. 1962 Turbulent thermal convection at arbitrary Prandtl number. Phys. Fluids 5 (11), 1374–1389.CrossRefGoogle Scholar
Lam, S., Shang, X.-D., Zhou, S.-Q. & Xia, K.-Q. 2002 Prandtl number dependence of the viscous boundary layer and the Reynolds numbers in Rayleigh–Bénard convection. Phys. Rev. E 65 (6), 066306.CrossRefGoogle ScholarPubMed
Landau, L.D. & Lifschitz, E.M. 1987 Fluid Mechanics, 2nd edn. Pergamon.Google Scholar
Li, L., Shi, N., Du Puits, R., Resagk, C., Schumacher, J. & Thess, A. 2012 Boundary layer analysis in turbulent Rayleigh–Bénard convection in air: experiment versus simulation. Phys. Rev. E 86 (2), 026315.CrossRefGoogle ScholarPubMed
Li, X.-M., Huang, S.-D., Ni, R. & Xia, K.-Q. 2021 Lagrangian velocity and acceleration measurements in plume-rich regions of turbulent Rayleigh–Bénard convection. Phys. Rev. Fluids 6 (5), 053503.CrossRefGoogle Scholar
Lohse, D. & Xia, K.-Q. 2010 Small-scale properties of turbulent Rayleigh–Bénard convection. Annu. Rev. Fluid Mech. 42, 335–364.CrossRefGoogle Scholar
Ni, R., Huang, S.-D. & Xia, K.-Q. 2011 Local energy dissipation rate balances local heat flux in the center of turbulent thermal convection. Phys. Rev. Lett. 107 (17), 174503.CrossRefGoogle Scholar
Petschel, K., Stellmach, S., Wilczek, M., Lülff, J. & Hansen, U. 2013 Dissipation layers in Rayleigh–Bénard convection: a unifying view. Phys. Rev. Lett. 110 (11), 114502.CrossRefGoogle ScholarPubMed
du Puits, R., Resagk, C. & Thess, A. 2007 Mean velocity profile in confined turbulent convection. Phys. Rev. Lett. 99 (23), 234504.CrossRefGoogle ScholarPubMed
Roche, P.-E., Gauthier, F., Kaiser, R. & Salort, J. 2010 On the triggering of the ultimate regime of convection. New J. Phys. 12 (8), 085014.CrossRefGoogle Scholar
Scheel, J.D. & Schumacher, J. 2014 Local boundary layer scales in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 758, 344–373.CrossRefGoogle Scholar
Schlichting, H. & Gersten, K. 2017 Boundary-layer Theory, 9th edn. Springer-Verlag.CrossRefGoogle Scholar
Schumacher, J., Bandaru, V., Pandey, A. & Scheel, J.D. 2016 Transitional boundary layers in low-Prandtl-number convection. Phys. Rev. Fluids 1 (8), 084402.CrossRefGoogle Scholar
Shishkina, O., Horn, S., Wagner, S. & Ching, E.S.C. 2015 Thermal boundary layer equation for turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 114 (11), 114302.CrossRefGoogle ScholarPubMed
Stevens, R.J.A.M., Zhou, Q., Grossmann, S., Verzicco, R., Xia, K.-Q. & Lohse, D. 2012 Thermal boundary layer profiles in turbulent Rayleigh–Bénard convection in a cylindrical sample. Phys. Rev. E 85 (2), 027301.CrossRefGoogle Scholar
Sun, C., Cheung, Y.-H. & Xia, K.-Q. 2008 Experimental studies of the viscous boundary layer properties in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 605, 79–113.CrossRefGoogle Scholar
Sun, C. & Xia, K.-Q. 2005 Scaling of the Reynolds number in turbulent thermal convection. Phys. Rev. E 72 (6), 067302.CrossRefGoogle ScholarPubMed
Sun, C., Xia, K.-Q. & Tong, P. 2005 Three-dimensional flow structures and dynamics of turbulent thermal convection in a cylindrical cell. Phys. Rev. E 72 (2), 026302.CrossRefGoogle Scholar
Thielicke, W. & Sonntag, R. 2021 Particle image velocimetry for MATLAB: accuracy and enhanced algorithms in PIVlab. J. Open Res. Softw. 9, 12.CrossRefGoogle Scholar
Tilgner, A., Belmonte, A. & Libchaber, A. 1993 Temperature and velocity profiles of turbulent convection in water. Phys. Rev. E 47 (4), R2253–R2256.CrossRefGoogle ScholarPubMed
Verzicco, R. & Camussi, R. 2003 Numerical experiments on strongly turbulent thermal convection in a slender cylindrical cell. J. Fluid Mech. 477, 19–49.CrossRefGoogle Scholar
Vogt, T., Horn, S., Grannan, A.M. & Aurnou, J.M. 2018 Jump rope vortex in liquid metal convection. Proc. Natl Acad. Sci. USA 115 (50), 12674–12679.CrossRefGoogle ScholarPubMed
Wei, P. & Xia, K.-Q. 2013 Viscous boundary layer properties in turbulent thermal convection in a cylindrical cell: the effect of cell tilting. J. Fluid Mech. 720, 140–168.CrossRefGoogle Scholar
Xi, H.-D. & Xia, K.-Q. 2008 Flow mode transitions in turbulent thermal convection. Phys. Fluids 20 (5), 055104.CrossRefGoogle Scholar
Xi, H.-D., Zhou, Q. & Xia, K.-Q. 2006 Azimuthal motion of the mean wind in turbulent thermal convection. Phys. Rev. E 73 (5), 056312.CrossRefGoogle ScholarPubMed
Xi, H.-D., Zhou, S.-Q., Zhou, Q., Chan, T.-S. & Xia, K.-Q. 2009 Origin of the temperature oscillation in turbulent thermal convection. Phys. Rev. Lett. 102 (4), 044503.CrossRefGoogle ScholarPubMed
Xia, K.-Q. 2013 Current trends and future directions in turbulent thermal convection. Theor. Appl. Mech. Lett. 3 (5), 052001.CrossRefGoogle Scholar
Xia, K.-Q., Sun, C. & Zhou, S.-Q. 2003 Particle image velocimetry measurement of the velocity field in turbulent thermal convection. Phys. Rev. E 68 (6), 066303.CrossRefGoogle ScholarPubMed
Xin, Y.-B. & Xia, K.-Q. 1997 Boundary layer length scales in convective turbulence. Phys. Rev. E 56 (3), 3010–3015.CrossRefGoogle Scholar
Xin, Y.-B., Xia, K.-Q. & Tong, P. 1996 Measured velocity boundary layers in turbulent convection. Phys. Rev. Lett. 77 (7), 1266–1269.CrossRefGoogle ScholarPubMed
Xu, W., Wang, Y., He, X., Wang, X., Schumacher, J., Huang, S.-D. & Tong, P. 2021 Mean velocity and temperature profiles in turbulent Rayleigh–Bénard convection at low Prandtl numbers. J. Fluid Mech. 918, A1.CrossRefGoogle Scholar
Zhang, L., Ding, G.-Y. & Xia, K.-Q. 2021 On the effective horizontal buoyancy in turbulent thermal convection generated by cell tilting. J. Fluid Mech. 914, A15.CrossRefGoogle Scholar
Zhang, L., Dong, J. & Xia, K.-Q. 2022 Exploring the plume and shear effects in turbulent Rayleigh–Bénard convection with effective horizontal buoyancy under streamwise and spanwise geometrical confinements. J. Fluid Mech. 940, A37.CrossRefGoogle Scholar
Zhou, Q., Stevens, R.J.A.M., Sugiyama, K., Grossmann, S., Lohse, D. & Xia, K.-Q. 2010 Prandtl-Blasius temperature and velocity boundary-layer profiles in turbulent Rayleigh–Bénard convection. J. Fluid Mech. 664, 297–312.CrossRefGoogle Scholar
Zhou, Q., Xi, H.-D., Zhou, S.-Q., Sun, C. & Xia, K.-Q. 2009 Oscillations of the large-scale circulation in turbulent Rayleigh–Bénard convection: the sloshing mode and its relationship with the torsional mode. J. Fluid Mech. 630, 367–390.CrossRefGoogle Scholar
Zhou, Q. & Xia, K.-Q. 2010 Measured instantaneous viscous boundary layer in turbulent Rayleigh–Bénard convection. Phys. Rev. Lett. 104 (10), 104301.CrossRefGoogle ScholarPubMed
Zhu, X. & Zhou, Q. 2021 Flow structures of turbulent Rayleigh–Bénard convection in annular cells with aspect ratio one and larger. Acta Mechanica Sin. 37 (8), 1291–1298.CrossRefGoogle Scholar
Zou, H.Y., Zhou, W.-F., Chen, X., Bao, Y., Chen, J. & She, Z.-S. 2019 Boundary layer structure in turbulent Rayleigh–Bénard convection in a slim box. Acta Mechanica Sin. 35 (4), 713–728.CrossRefGoogle Scholar