Hostname: page-component-cd9895bd7-fscjk Total loading time: 0 Render date: 2024-12-29T12:44:00.120Z Has data issue: false hasContentIssue false
  • English
  • Français

The three-dimensional structure of swirl-switching in bent pipe flow

Published online by Cambridge University Press:  27 November 2017

Lorenz Hufnagel ,
Jacopo Canton Open the ORCID record for Jacopo Canton [Opens in a new window] ,
Ramis Örlü Open the ORCID record for Ramis Örlü [Opens in a new window] ,
Oana Marin ,
Elia Merzari  and
Philipp Schlatter Open the ORCID record for Philipp Schlatter [Opens in a new window]
Lorenz Hufnagel
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
Jacopo Canton*
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
Ramis Örlü
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
Oana Marin
Affiliation:
Mathematics and Computer Science Division, Argonne National Laboratory, Lemont, IL 60439, USA
Elia Merzari
Affiliation:
Mathematics and Computer Science Division, Argonne National Laboratory, Lemont, IL 60439, USA
Philipp Schlatter
Affiliation:
Linné FLOW Centre and Swedish e-Science Research Centre (SeRC), KTH Mechanics, Royal Institute of Technology, SE-100 44 Stockholm, Sweden
*
†Email address for correspondence: jcanton@mech.kth.se
Get access Rights & Permissions [Opens in a new window]

Abstract

Swirl-switching is a low-frequency oscillatory phenomenon which affects the Dean vortices in bent pipes and may cause fatigue in piping systems. Despite thirty years worth of research, the mechanism that causes these oscillations and the frequencies that characterise them remain unclear. Here we show that a three-dimensional wave-like structure is responsible for the low-frequency switching of the dominant Dean vortex. 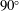The present study, performed via direct numerical simulation, focuses on the turbulent flow through a $90^{\circ }$ pipe bend preceded and followed by straight pipe segments. A pipe with curvature 0.3 (defined as ratio between pipe radius and bend radius) is studied for a bulk Reynolds number 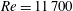$Re=11\,700$, corresponding to a friction Reynolds number 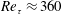$Re_{\unicode[STIX]{x1D70F}}\approx 360$. Synthetic turbulence is generated at the inflow section and used instead of the classical recycling method in order to avoid the interference between recycling and swirl-switching frequencies. The flow field is analysed by three-dimensional proper orthogonal decomposition (POD) which for the first time allows the identification of the source of swirl-switching: a wave-like structure that originates in the pipe bend. Contrary to some previous studies, the flow in the upstream pipe does not show any direct influence on the swirl-switching modes. Our analysis further shows that a three-dimensional characterisation of the modes is crucial to understand the mechanism, and that reconstructions based on two-dimensional POD modes are incomplete.

JFM classification

Boundary Layers: Pipe flow boundary layer Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent Flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 835 , 25 January 2018 , pp. 86 - 101
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Anwer, M., So, R. M. C. & Lai, Y. G. 1989 Perturbation by and recovery from bend curvature of a fully developed turbulent pipe flow. Phys. Fluids 1, 1387–1397.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25, 539–575.CrossRefGoogle Scholar
Boussinesq, M. J. 1868 Mémoire sur l’influence des frottements dans les mouvements réguliers des fluides. J. Math. Pure Appl. 13, 377–424.Google Scholar
Brücker, C. 1998 A time-recording DPIV-study of the swirl-switching effect in a 90° bend flow. In Proc. 8th Int. Symp. Flow Vis., Sorrento (NA), Italy; pp. 171.1–171.6. Springer.Google Scholar
Canton, J., Örlü, R. & Schlatter, P. 2017 Characterisation of the steady, laminar incompressible flow in toroidal pipes covering the entire curvature range. Intl J. Heat Fluid Flow 66, 95–107.CrossRefGoogle Scholar
Canton, J., Schlatter, P. & Örlü, R. 2016 Modal instability of the flow in a toroidal pipe. J. Fluid Mech. 792, 894–909.CrossRefGoogle Scholar
Carlsson, C., Alenius, E. & Fuchs, L. 2015 Swirl switching in turbulent flow through 90° pipe bends. Phys. Fluids 27, 085112.CrossRefGoogle Scholar
Chandler, R. & Northrop, P.2003 Fortran random number generation. http://www.ucl.ac.uk/∼ucakarc/work/randgen.html.Google Scholar
Chung, Y. M. & Wang, Z. 2017 Direct numerical simulation of a turbulent curved pipe flow with a 90° bend. In 10th Int. Symp. Turbul. Shear Flow Phenom., Chicago.Google Scholar
Dean, W. R. 1928 The streamline motion of fluid in a curved pipe. Phil. Mag. 5, 673–693.CrossRefGoogle Scholar
Doherty, J., Monty, J. & Chong, M. 2007 The development of turbulent pipe flow. In 16th Australas. Fluid Mech. Conf., pp. 266–270. The Australasian Fluid Mechanics Society.Google Scholar
El Khoury, G. K., Schlatter, P., Noorani, A., Fischer, P. F., Brethouwer, G. & Johansson, A. V. 2013 Direct numerical simulation of turbulent pipe flow at moderately high Reynolds numbers. Flow Turbul. Combust. 91, 475–495.CrossRefGoogle Scholar
Eustice, J. 1910 Flow of water in curved pipes. Proc. R. Soc. Lond. A 84, 107–118.Google Scholar
Fischer, P. F., Lottes, J. W. & Kerkemeier, S. G.2008 Nek5000 Web page http://nek5000.mcs.anl.gov.Google Scholar
Hellström, L. H. O., Zlatinov, M. B., Cao, G. & Smits, A. J. 2013 Turbulent pipe flow downstream of a 90° bend. J. Fluid Mech. 735, R7.CrossRefGoogle Scholar
Hof, B., van Doorne, C. W. H., Westerweel, J., Nieuwstadt, F. T. M., Faisst, H., Eckhardt, B., Wedin, H., Kerswell, R. R. & Waleffe, F. 2004 Experimental observation of nonlinear traveling waves in turbulent pipe flow. Science 305, 1594–1598.CrossRefGoogle ScholarPubMed
Hufnagel, L.2016 On the swirl-switching in developing bent pipe flow with direct numerical simulation. Msc thesis, KTH Mechanics, Stockholm, Sweden.Google Scholar
Jarrin, N., Benhamadouche, S., Laurence, D. & Prosser, R. 2006 A synthetic-eddy-method for generating inflow conditions for large-eddy simulations. Intl J. Heat Fluid Flow 27, 585–593.CrossRefGoogle Scholar
Kalpakli, A. & Örlü, R. 2013 Turbulent pipe flow downstream a 90° pipe bend with and without superimposed swirl. Intl J. Heat Fluid Flow 41, 103–111.CrossRefGoogle Scholar
Kalpakli Vester, A., Örlü, R. & Alfredsson, P. H. 2015 POD analysis of the turbulent flow downstream a mild and sharp bend. Exp. Fluids 56, 57.CrossRefGoogle Scholar
Kalpakli Vester, A., Örlü, R. & Alfredsson, P. H. 2016 Turbulent flows in curved pipes: recent advances in experiments and simulations. Appl. Mech. Rev. 68, 050802.CrossRefGoogle Scholar
Kühnen, J., Braunshier, P., Schwegel, M., Kuhlmann, H. C. & Hof, B. 2015 Subcritical versus supercritical transition to turbulence in curved pipes. J. Fluid Mech. 770, R3.CrossRefGoogle Scholar
Kühnen, J., Holzner, M., Hof, B. & Kuhlmann, H. C. 2014 Experimental investigation of transitional flow in a toroidal pipe. J. Fluid Mech. 738, 463–491.CrossRefGoogle Scholar
Lumley, J. L. 1967 The structure of inhomogeneous turbulent flows. In Atmos. Turbul. Radio Wave Propag. (ed. Yaglom, A. M. & Tatarski, V. I.), pp. 166–178. Nauka.Google Scholar
Manhart, M. & Wengle, H. 1993 A spatiotemporal decomposition of a fully inhomogeneous turbulent flow field. Theor. Comput. Fluid Dyn. 5, 223–242.CrossRefGoogle Scholar
Noorani, A., El Khoury, G. K. & Schlatter, P. 2013 Evolution of turbulence characteristics from straight to curved pipes. Intl J. Heat Fluid Flow 41, 16–26.CrossRefGoogle Scholar
Noorani, A. & Schlatter, P. 2016 Swirl-switching phenomenon in turbulent flow through toroidal pipes. Intl J. Heat Fluid Flow 61, 108–116.CrossRefGoogle Scholar
Poletto, R., Craft, T. & Revell, A. 2013 A new divergence free synthetic eddy method for the reproduction of inlet flow conditions for LES. Flow Turbul. Combust. 91, 519–539.CrossRefGoogle Scholar
Poletto, R., Revell, A., Craft, T. J. & Jarrin, N. 2011 Divergence free synthetic eddy method for embedded LES inflow boundary conditions. In 7th Int. Symp. Turbul. Shear Flow Phenom., Ottawa.Google Scholar
Rütten, F., Meinke, M. & Schröder, W. 2001 Large-eddy simulations of 90° pipe bend flows. J. Turbul. 2, N3.CrossRefGoogle Scholar
Rütten, F., Schröder, W. & Meinke, M. 2005 Large-eddy simulation of low frequency oscillations of the Dean vortices in turbulent pipe bend flows. Phys. Fluids 17, 035107.CrossRefGoogle Scholar
Sakakibara, J. & Machida, N. 2012 Measurement of turbulent flow upstream and downstream of a circular pipe bend. Phys. Fluids 24, 041702.CrossRefGoogle Scholar
Sakakibara, J., Sonobe, R., Goto, H., Tezuka, H., Tada, H. & Tezuka, K. 2010 Stereo-PIV study of turbulent flow downstream of a bend in a round pipe. In 14th Int. Symp. Flow Vis., EXCO Daegu, Korea, Springer.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.CrossRefGoogle Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Maths 45, 561–571.CrossRefGoogle Scholar
Sudo, K., Sumida, M. & Hibara, H. 1998 Experimental investigation on turbulent flow in a circular-sectioned 90-degree bend. Exp. Fluids 25, 42–49.CrossRefGoogle Scholar
Tunstall, M. J. & Harvey, J. K. 1968 On the effect of a sharp bend in a fully developed turbulent pipe-flow. J. Fluid Mech. 34, 595–608.CrossRefGoogle Scholar
Vashisth, S., Kumar, V. & Nigam, K. D. P. 2008 A review on the potential applications of curved geometries in process industry. Ind. Engng Chem. Res. 47, 3291–3337.CrossRefGoogle Scholar

Hufnagel et al. supplementary movie 1

Instantaneous flow field in the bent pipe depicted by pseudocolors of velocity magnitude.

Download Hufnagel et al. supplementary movie 1(Video)
Video 90.8 MB

Hufnagel et al. supplementary movie 2

Reconstruction of the flow field based on modes 0-2 extracted by three-dimensional POD.

Download Hufnagel et al. supplementary movie 2(Video)
Video 18.7 MB

Hufnagel et al. supplementary movie 3

Reconstruction of the flow field based on modes 0-4 extracted by three-dimensional POD. The large view clearly shows the travelling wave responsible for the swirl-switching, which is visible in the two cross-flow sections. See figure 5 for a static view of the modes.

Download Hufnagel et al. supplementary movie 3(Video)
Video 20.5 MB