Hostname: page-component-cd9895bd7-7cvxr Total loading time: 0 Render date: 2024-12-28T05:39:25.854Z Has data issue: false hasContentIssue false
  • English
  • Français

Three-dimensionality in the wake of a rotating cylinder in a uniform flow

Published online by Cambridge University Press:  01 February 2013

A. Rao ,
J. Leontini ,
M. C. Thompson  and
K. Hourigan
A. Rao
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
J. Leontini*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
M. C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia
K. Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, Victoria 3800, Australia Division of Biological Engineering, Monash University, Melbourne, Victoria 3800, Australia
*
†Email address for correspondence: justin.leontini@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

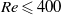The wake of a rotating circular cylinder in a free stream is investigated for Reynolds numbers $\mathit{Re}\leqslant 400$ and non-dimensional rotation rates of 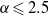$\alpha \leqslant 2. 5$. Two aspects are considered. The first is the transition from a steady flow to unsteady flow characterized by periodic vortex shedding. The two-dimensional computations show that the onset of unsteady flow is delayed to higher Reynolds numbers as the rotation rate is increased, and vortex shedding is suppressed for 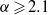$\alpha \geqslant 2. 1$ for all Reynolds numbers in the parameter space investigated. The second aspect investigated is the transition from two-dimensional to three-dimensional flow using linear stability analysis. It is shown that at low rotation rates of 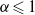$\alpha \leqslant 1$, the three-dimensional transition scenario is similar to that of the non-rotating cylinder. However, at higher rotation rates, the three-dimensional scenario becomes increasingly complex, with three new modes identified that bifurcate from the unsteady flow, and two modes that bifurcate from the steady flow. Curves of marginal stability for all of the modes are presented in a parameter space map, the defining characteristics for each mode presented, and the physical mechanisms of instability are discussed.

JFM classification

Instability: Parametric instability Vortex Flows: Vortex shedding Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 1 - 29
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akoury, R. El, Braza, M., Perrin, R., Harran, G. & Hoarau, Y. 2008 The three-dimensional transition in the flow around a rotating cylinder. J. Fluid Mech. 607, 1–11.CrossRefGoogle Scholar
Badr, H. M., Coutanceau, M., Dennis, S. C. R. & Menard, C. 1990 Unsteady flow past a rotating circular cylinder at Reynolds numbers $1{0}^{3} $ and $1{0}^{4} $ . J. Fluid Mech. 220, 459–484.CrossRefGoogle Scholar
Badr, H. M., Dennis, S. C. R. & Young, P. J. S. 1989 Steady and unsteady flow past a rotating circular cylinder at low Reynolds numbers. Comput. Fluids 17 (4), 579–609.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Barkley, D., Tuckerman, L. S. & Golubitsky, M. 2000 Bifurcation theory for three-dimensional flow in the wake of a circular cylinder. Phys. Rev. E 61, 5247–5252.CrossRefGoogle ScholarPubMed
Bayly, B. J. 1988 Three-dimensional centrifugal-type instabilities in inviscid two-dimensional flows. Phys. Fluids 31, 56–64.Google Scholar
Billant, P. & Gallaire, F. 2005 Generalised Rayleigh criterion for non-axisymmetric centrifugal instabilities. J. Fluid Mech. 542, 365–379.CrossRefGoogle Scholar
Blackburn, H. M. & Lopez, J. M. 2003 On three-dimensional quasiperiodic Floquet instabilities of two-dimensional bluff body wakes. Phys. Fluids 15, L57–L60.CrossRefGoogle Scholar
Blackburn, H. M., Marques, F. & Lopez, J. M. 2005 Symmetry breaking of two-dimensional time-periodic wakes. J. Fluid Mech. 552, 395–411.Google Scholar
Chen, Y.-M., Ou, Y.-R. & Pearlstein, A. J. 1993 Development of the wake behind a circular cylinder impulsively started into rotatory and rectilinear motion. J. Fluid Mech. 253, 449–484.CrossRefGoogle Scholar
Chew, Y. T., Cheng, M. & Luo, S. C. 1995 A numerical study of flow past a rotating circular cylinder using a hybrid vortex scheme. J. Fluid Mech. 299, 35–71.Google Scholar
Gallaire, F., Marquille, M. & Ehrenstein, U. 2007 Three-dimensional transverse instabilities in detached boundary layers. J. Fluid Mech. 571, 221–233.Google Scholar
Görtler, H. 1955 Dreidimensionales zur stabilitätstheorie laminarer grenzschichten. Z. Angew. Math. Mech. 35 (9–10), 362–363.Google Scholar
Griffith, M. D., Thompson, M. C., Leweke, T., Hourigan, K. & Anderson, W. P. 2007 Wake behaviour and instability of flow through a partially blocked channel. J. Fluid Mech. 582, 319–340.CrossRefGoogle Scholar
Ingham, D. B. 1983 Steady flow past a rotating cylinder. Comput. Fluids 11 (4), 351–366.Google Scholar
Kang, S. M., Choi, H. C. & Lee, S. 1999 Laminar flow past a rotating circular cylinder. Phys. Fluids 11 (11), 3312–3321.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 2005 Spectral/hp Methods for Computational Fluid Dynamics. Oxford University Press.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.CrossRefGoogle Scholar
Kumar, S., Cantu, C. & Gonzalez, B. 2011 Flow past a rotating cylinder at low and high rotation rates. J. Fluids Engng 133 (4), 041201.Google Scholar
Lagnado, R. R., Phan-Thien, N. & Leal, L. G. 1983 The stability of two-dimensional linear flow. In Proceedings of the Eighth Australasian Fluid Mechanics Conference, pp. 7A5–7A7. University of Newcastle.Google Scholar
Leblanc, S. & Godeferd, F. S. 1999 An illustration of the link between ribs and hyperbolic instability. Phys. Fluids 11 (2), 497–499.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.CrossRefGoogle Scholar
Leweke, T. & Williamson, C. H. K. 1998 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85–119.CrossRefGoogle Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf-bifurcation in spherical Couette flow. Phys. Fluids 7 (1), 80–91.Google Scholar
Meena, J., Sidharth, G. S., Khan, M. H. & Mittal, S. 2011 Three-dimensional instabilities in flow past a spinning and translating cylinder. In IUTAM Symposium on Bluff Body Flows, IIT-Kanpur, India, pp. 59–62.Google Scholar
Mittal, S. 2004 Three-dimensional instabilities in flow past a rotating cylinder. J. Appl. Mech. 71 (1), 89–95.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Pralits, J. O., Brandt, L. & Giannetti, F. 2010 Instability and sensitivity of the flow around a rotating circular cylinder. J. Fluid Mech. 650, 513–536.CrossRefGoogle Scholar
Prandtl, L. 1926 Application of the ‘Magnus effect’ to the wind propulsion of ships, National Advisory Committee for Aeronautics, Technical memorandum, 367.Google Scholar
Rao, A., Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2011 Flows past rotating cylinders next to a wall. J. Fluids Struct. 27 (5–6), 668–679.CrossRefGoogle Scholar
Rayleigh, Lord 1917 On the dynamics of revolving fluids. Proc. R. Soc. Lond. A 93, 148–154.Google Scholar
Sheard, G. J. 2011 Wake stability features behind a square cylinder: focus on small incidence angles. J. Fluids Struct. 27 (5–6), 734–742.CrossRefGoogle Scholar
Sheard, G. J., Fitzgerald, M. J. & Ryan, K. 2009 Cylinders with square cross-section: wake instabilities with incidence angle variation. J. Fluid Mech. 630, 43–69.Google Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2003 From spheres to circular cylinders: the stability and flow structures of bluff ring wakes. J. Fluid Mech. 492, 147–180.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C. & Hourigan, K. 2005a Subharmonic mechanism of the mode C instability. Phys. Fluids 17 (11), 1–4.CrossRefGoogle Scholar
Sheard, G. J., Thompson, M. C., Hourigan, K. & Leweke, T. 2005b The evolution of a subharmonic mode in a vortex street. J. Fluid Mech. 534, 23–38.CrossRefGoogle Scholar
Sipp, D. & Jacquin, L. 2000 Three-dimensional centrifugal-type instabilities of two-dimensional flows in rotating systems. Phys. Fluids 12, 1740–1748.Google Scholar
Stewart, B. E., Hourigan, K., Thompson, M. C. & Leweke, T. 2006 Flow dynamics and forces associated with a cylinder rolling along a wall. Phys. Fluids 18 (11), 111701.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.CrossRefGoogle Scholar
Stojković, D., Breuer, M. & Durst, F. 2002 Effect of high rotation rates on the laminar flow around a circular cylinder. Phys. Fluids 14 (9), 3160–3178.Google Scholar
Stojković, D., Schön, P., Breuer, M. & Durst, F. 2003 On the new vortex shedding mode past a rotating circular cylinder. Phys. Fluids 15 (5), 1257–1260.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006a Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 190–196.Google Scholar
Thompson, M. C., Hourigan, K., Ryan, K. & Sheard, G. J. 2006b Wake transition of two-dimensional cylinders and axisymmetric bluff bodies. J. Fluids Struct. 22, 793–806.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001 The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Williamson, C. H. K. 1996a Three-dimensional vortex dynamics in bluff body wakes. Exp. Therm. Fluid Sci. 12, 150–168.Google Scholar
Williamson, C. H. K. 1996b Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Williamson, C & Brown, G. L. 1998 A series in $1/ \sqrt{\mathit{Re}} $ to represent the Strouhal–Reynolds number relationship of the cylinder wake. J. Fluids Struct. 12, 1073–1085.Google Scholar
Zhang, H.-Q., Fey, U., Noack, B. R., Konig, M. & Eckelemann, H. 1995 On the transition of the cylinder wake. Phys. Fluids 7 (4), 779–794.Google Scholar