Hostname: page-component-78c5997874-xbtfd Total loading time: 0 Render date: 2024-11-15T02:06:17.917Z Has data issue: false hasContentIssue false
  • English
  • Français

Tracer particle momentum effects in vortex flows

Published online by Cambridge University Press:  16 April 2013

David M. Birch  and
Nicholas Martin
David M. Birch*
Affiliation:
Department of Mechanical Engineering Sciences, University of Surrey, Guildford, Surrey GU2 7XH, UK
Nicholas Martin
Affiliation:
Department of Mechanical Engineering Sciences, University of Surrey, Guildford, Surrey GU2 7XH, UK
*
†Email address for correspondence: d.birch@surrey.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

The measurement of vortex flows with particle-image velocimetry (PIV) is particularly susceptible to error arising from the finite mass of the tracer particles, owing to the high velocities and accelerations typically experienced. 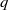A classical model of Stokes-flow particle transport is adopted, and an approximate solution for the case of particle transport within an axisymmetric, quasi-two-dimensional Batchelor $q$-vortex is presented. A generalized expression for the maximum particle tracking error is proposed for each of the velocity components, and the importance of finite particle size distributions is discussed. The results indicate that the tangential velocity component is significantly less sensitive to tracking error than the radial component, and that the conventional particle selection criterion (based on the particle Stokes number) may result in either over- or under-sized particles for a specified allowable error bound. Results were demonstrated by means of PIV measurements carried out in air and water using particles with very different properties.

JFM classification

Multiphase and Particle-laden Flows: Multiphase and Particle-laden Flows Vortex Flows: Vortex Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 723 , 25 May 2013 , pp. 665 - 691
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bailey, S. C. C. & Tavoularis, S. 2008 Measurements of the velocity field of a wing-tip vortex, wandering in grid turbulence. J. Fluid Mech. 601, 281–315.CrossRefGoogle Scholar
Bailey, S. C. C., Tavoularis, S. & Lee, B. H. K. 2006 Effects of free stream turbulence on wing-tip vortex formation and near field. J. Aircraft 43 (5), 1282–1291.Google Scholar
Bandyopadhyay, P., Stead, D. & Ash, R. 1991 Organized nature of a turbulent trailing vortex. AIAA J. 29, 1627–1633.Google Scholar
Batchelor, G. K. 1964 Axial flow in trailing line vortices. J. Fluid Mech. 20, 645–658.Google Scholar
Beninati, M. & Marshall, J. 2005 An experimental study of the effect of free-stream turbulence on a trailing vortex. Exp. Fluids 38, 244–257.Google Scholar
Beresh, S. J., Henfling, J. F. & Spillers, R. W. 2010 Meander of a fin trailing vortex and the origin of its turbulence. Exp. Fluids 49, 599–611.Google Scholar
Birch, D. M. 2012 Self-similarity of trailing vortices. Phys. Fluids 24 (3), 1–16.Google Scholar
Birch, D. M. & Lee, T. 2005 Investigation of the near-field tip vortex behind an oscillating wing. J. Fluid Mech. 544, 201–241.Google Scholar
Birch, D. M., Lee, T., Mokhtarian, F. & Kafyeke, F. 2004 Structure and induced drag of a tip vortex. J. Aircraft 41 (5), 1138–1145.Google Scholar
Brown, M. R., MacInnes, J. M. & Allen, R. W. K. 2007 Three-component micro-piv using the continuity equation and a comparison of the performance with that of stereoscopic measurements. Exp. Fluids 42 (2), 197–205.Google Scholar
Chow, J., Zilliac, G. & Bradshaw, P. 1997 Mean and turbulence measurements in the near field of a wingtip vortex. AIAA J. 35 (10), 1561–1567.Google Scholar
Dacles-Mariani, J., Zilliac, G. G., Chow, J. S. & Bradshaw, P. 1995 Numerical/experimental study of a wingtip vortex in the near field. AIAA J. 33 (9), 1561–1568.Google Scholar
Devenport, W. J., Rife, M. C., Liapis, S. I. & Follin, G. J. 1996 The structure and development of a wing-tip vortex. J. Fluid Mech. 312, 67–106.Google Scholar
Dring, R. P. 1982 Sizing criteria for laser anemometry particles. Trans. ASME: J. Fluids Engng 104 (1).Google Scholar
Goto, S. 2008 A physical mechanism of the energy cascade in homogeneous isotropic turbulence. J. Fluid Mech. 605, 355–366.CrossRefGoogle Scholar
Grant, I., Pan, X., Wang, X. & Stewart, N. 1994 Correction for viewing angle applied to piv data obtained in aerodynamic blade vortex interaction studies. Exp. Fluids 18 (1–2), 95–99.Google Scholar
Greenwell, D. I. 2002 Effect of tracer particle characteristics on visualization of delta wing vortices. Aeronaut. J. 106 (1063), 473–482.Google Scholar
Hart, D. P. 2000 Super-resolution PIV by recursive local-correlation. J. Vis. 3 (2), 187–194.CrossRefGoogle Scholar
Hoffman, E. R. & Joubert, P. N. 1963 Turbulent line vortices. J. Fluid Mech. 16, 395–411.Google Scholar
Iungo, G. V., Skinner, P. & Buresti, G. 2009 Correction of wandering smoothing effects on static measurements of a wing-tip vortex. Exp. Fluids 46, 435–452.Google Scholar
van Jaarsveld, J. P. J., Holten, A. P. C., Elsenaar, A., Trieling, R. R. & van Heijst, G. J. F. 2011 An experimental study of the effect of external turbulence on the decay of a single vortex and a vortex pair. J. Fluid Mech. 670, 214–239.Google Scholar
Kriebel, A. R. 1961 Particle trajectories in a gas centrifuge. Trans. ASME: J. Basic Engng 83 (3), 333–340.Google Scholar
Leishman, J. G. 1996 Seed particle dynamics in tip vortex flows. J. Aircraft 33 (4), 823–825.CrossRefGoogle Scholar
Martin, W. T., Kadambi, J. R. & Wernet, M. P. 1997 Particle imaging technique for size, velocity, and concentration measurements in particle laden flows. Proc. SPIE – Int. Soc. Optical Eng. 3172, 518–529.Google Scholar
Martinelli, F., Olivani, A. & Coghe, A. 2007 Experimental analysis of the precessing vortex core in a free swirling jet. Exp. Fluids 42, 827–839.Google Scholar
Maxey, R. & Riley, J. J. 1983 Equation of motion for a small rigid sphere in a non uniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Melling, A. 1997 Tracer particles and seeding for particle image velocimetry. Meas. Sci. Technol. 8, 1406–1416.Google Scholar
Meunier, P., Ehrenstein, U., Leweke, T. & Rossi, M. 2002 A merging criterion for two-dimensional co-rotating vortices. Phys. Fluids 14 (8), 2757–2766.Google Scholar
Paiva, J., Salcedo, R. & Araujo, P. 2010 Impact of particle agglomeration in cyclones. Chem. Engng J. 162 (3), 861–876.Google Scholar
Phillips, W. R. C. 1981 The turbulent trailing vortex during roll-up. J. Fluid Mech. 105, 451–467.CrossRefGoogle Scholar
Phillips, W. R. C. & Graham, J. 1984 Reynolds-stress measurements in a turbulent trailing vortex. J. Fluid Mech. 147, 353–371.CrossRefGoogle Scholar
Ramasamy, M., Johnson, B. & Leishman, J. G. 2009 Turbulent tip vortex measurements using dual-plane stereoscopic particle image velocimetry. AIAA J. 47 (8), 1826–1840.Google Scholar
Regunath, G. S., Zimmerman, W. B., Tesar, V. & Hewakandamby, B. N. 2008 Experimental investigation of helicity in turbulent swirling jet using dual-plane dye laser piv technique. Exp. Fluids 45 (6), 973–986.CrossRefGoogle Scholar
Rossow, V. J. 1999 Lift-generated vortex wakes of subsonic transport aircraft. Prog. Aerosp. Sci. 35, 507–660.Google Scholar
Saffman, P. G. 1965 The lift on a small sphere in a slow shear flow. J. Fluid Mech. 22 (2), 385–400.Google Scholar
Spalart, P. 1998a Airplane trailing vortices. Annu. Rev. Fluid Mech. 30, 107–138.CrossRefGoogle Scholar
Spalart, P. 1998b On the far wake and induced drag of aircraft. J. Fluid Mech. 603, 413–430.Google Scholar
Tari, P. H., Gurka, R. & Hangan, H. 2010 Experimental investigation of tornado-like vortex dynamics with swirl ratio: the mean and turbulent flow fields. J. Wind Engng Ind. Aerodyn. 98, 936–944.Google Scholar
Tropea, C., Yarin, A. L. & Foss, J. F. 2007 Springer Handbook of Experimental Fluid Mechanics. Springer.Google Scholar
Uzun, A., Hussaini, M. Y. & Streett, C. L. 2006 Large-eddy simulation of a wing tip vortex on overset grids. AIAA J. 44 (6), 1229–1242.Google Scholar
Wang, L.-P. & Stock, D. E. 1993 Dispersion of heavy particles by turbulent motion. J. Atmos. Sci. 50 (13), 1897–1913.Google Scholar
Wereley, S. T. & Meinhart, C. D. 2001 Second-order accurate particle image velocimetry. Exp. Fluids 31, 258–268.Google Scholar
Widnall, S. 1975 The structure and dynamics of vortex filaments. Annu. Rev. Fluid Mech. 7, 141–165.Google Scholar
Zhang, W. & Sarkar, P. P. 2012 near-ground tornado-like vortex structure resolved by particle image velocimetry. Exp. Fluids 52, 479–493.Google Scholar