Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-28T05:40:56.212Z Has data issue: false hasContentIssue false
  • English
  • Français

Transient perturbation growth in time-dependent mixing layers

Published online by Cambridge University Press:  01 February 2013

C. Arratia ,
C. P. Caulfield  and
J.-M. Chomaz
C. Arratia
Affiliation:
LadHyX, CNRS-École Polytechnique, F-91128 Palaiseau, France
C. P. Caulfield
Affiliation:
BP Institute, University of Cambridge, Madingley Rise, Madingley Road, Cambridge CB3 0EZ, UK Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Centre for Mathematical Sciences, Wilberforce Road, Cambridge CB3 0WA, UK
J.-M. Chomaz
Affiliation:
LadHyX, CNRS-École Polytechnique, F-91128 Palaiseau, France
Get access Rights & Permissions [Opens in a new window]

Abstract

We investigate numerically the transient linear growth of three-dimensional (3D) perturbations in a homogeneous time-evolving mixing layer in order to identify which perturbations are optimal in terms of their kinetic energy gain over a finite, predetermined time interval. We model the mixing layer with an initial parallel velocity distribution 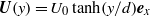$\mathbi{U}(y)= {U}_{0} \tanh (y/ d)\mathbi{e}_{x}$ with Reynolds number 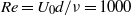$Re= {U}_{0} d/ \nu = 1000$, where $\nu $ is the kinematic viscosity of the fluid. We consider a range of time intervals on both a constant ‘frozen’ base flow and a time-dependent two-dimensional (2D) flow associated with the growth and nonlinear saturation of two wavelengths of the most-unstable eigenmode of linear theory of the initial parallel velocity distribution, which rolls up into two classical Rayleigh instabilities commonly referred to as Kelvin–Helmholtz (KH) billows, which eventually pair to form a larger vortex. For short times, the most-amplified perturbations on the frozen 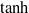$\tanh $ profile are inherently 3D, and are most appropriately described as oblique wave ‘OL’ perturbations which grow through a combination of the Orr and lift-up mechanisms, while for longer times, the optimal perturbations are 2D and similar to the KH normal mode, with a slight enhancement of gain. For the time-evolving KH base flow, OL perturbations continue to dominate over sufficiently short time intervals. However, for longer time intervals which involve substantial evolution of the primary KH billows, two broad classes of inherently 3D linear optimal perturbation arise, associated at low wavenumbers with the well-known core-centred elliptical translative instability, and at higher wavenumbers with the braid-centred hyperbolic instability. The hyperbolic perturbation is relatively inefficient in exploiting the gain of the OL perturbations, and so only dominates the smaller wavenumber (ultimately) core-centred perturbations when the time evolution of the base flow or the start time of the optimization interval does not allow the OL perturbations much opportunity to grow. When the OL perturbations can grow, they initially grow in the braid, and then trigger an elliptical core-centred perturbation by a strong coupling with the primary KH billow. If the optimization time interval includes pairing of the primary billows, the secondary elliptical perturbations are strongly suppressed during the pairing event, due to the significant disruption of the primary billow cores during pairing.

JFM classification

Boundary Layers: Free shear layers Instability: Instability Instability: Transition to turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 717 , 25 February 2013 , pp. 90 - 133
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antkowiak, A. & Brancher, P. 2007 On vortex rings around vortices: an optimal mechanism. J. Fluid Mech. 578, 295–304.Google Scholar
Basak, S. & Sarkar, S. 2006 Dynamics of a stratified shear layer with horizontal shear. J. Fluid Mech. 568, 19–54.Google Scholar
Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57 (17), 2160–2163.CrossRefGoogle ScholarPubMed
Brown, G. L. & Roshko, A. 1974 On density effects and large structure in turbulent mixing layers. J. Fluid Mech. 64, 775–816.CrossRefGoogle Scholar
Butler, K. M. & Farrell, B. F. 1992 Three-dimensional optimal perturbations in viscous shear flow. Phys. Fluids A 4, 1637–1650.Google Scholar
Caulfield, C. P. & Kerswell, R. R. 2000 The nonlinear development of three-dimensional disturbances at hyperbolic stagnation points: a model of the braid region in mixing layers. Phys. Fluids 12, 1032–1043.Google Scholar
Caulfield, C. P. & Peltier, W. R. 2000 The anatomy of the mixing transition in homogeneous and stratified free shear layers. J. Fluid Mech. 413, 1–47.Google Scholar
Corcos, G. M. & Lin, S. J. 1984 The mixing layer: deterministic models of a turbulent flow. Part 2. The origin of the three-dimensional motion. J. Fluid Mech. 139, 67–95.CrossRefGoogle Scholar
Corcos, G. M. & Sherman, F. S. 1984 The mixing layer: deterministic models of a turbulent flow. Part 1. Introduction and the two-dimensional flow. J. Fluid Mech. 139, 29–65.CrossRefGoogle Scholar
Dimotakis, P. E. 2005 Turbulent mixing. Annu. Rev. Fluid Mech. 37, 329–356.Google Scholar
Donnadieu, C., Ortiz, S., Chomaz, J.-M. & Billant, P. 2009 Three-dimensional instabilities and transient growth of a counter-rotating vortex pair. Phys. Fluids 21 (9), 094102.Google Scholar
Drazin, P. G. & Reid, W. H. 1981 Hydrodynamic Stability. Cambridge University Press.Google Scholar
Ellingsen, T. & Palm, E. 1975 Stability of linear flow. Phys. Fluids 18, 487–488.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993a Optimal excitation of three-dimensional perturbations in viscous constant shear flow. Phys. Fluids A 5, 1390–1400.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1993b Perturbation growth in shear flow exhibits universality. Phys. Fluids A 5, 2298–2300.Google Scholar
Farrell, B. F. & Ioannou, P. J. 1996 Generalized stability theory. Part II: nonautonomous operators. J. Atmos. Sci 53, 2041–2053.Google Scholar
Guegan, A., Huerre, P. & Schmid, P. J. 2007 Optimal disturbances in swept Hiemenz flow. J. Fluid Mech. 578, 223–232.CrossRefGoogle Scholar
Hazel, P. 1972 Numerical studies of the stability of inviscid stratified shear flows. J. Fluid Mech. 51, 39–61.Google Scholar
Hill, D. C. 1995 Adjoint systems and their role in the receptivity problem for boundary layers. J. Fluid Mech. 292, 183–204.CrossRefGoogle Scholar
Hussain, A. K. M. F. 1983 Turbulence and Chaotic Phenomena in Fluids (ed. Tatsumi, T.), pp. 453–460. North-Holland.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34, 83–113.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1985 The onset of turbulence in finite-amplitude Kelvin–Helmholtz billows. J. Fluid Mech. 155, 1–35.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1989 The role of transverse secondary instabilities in the evolution of free shear layers. J. Fluid Mech. 202, 367–402.Google Scholar
Klaassen, G. P. & Peltier, W. R. 1991 The influence of stratification on secondary instability in free shear layers. J. Fluid Mech. 227, 71–106.CrossRefGoogle Scholar
Landahl, M. T. 1980 A note on an algebraic instability of inviscid parallel shear flows. J. Fluid Mech. 98, 243–251.CrossRefGoogle Scholar
Lasheras, J. C. & Choi, H. 1988 Three-dimensional instability of a plane free shear layer: an experimental study of the formation and evolution of streamwise vortices. J. Fluid Mech. 189, 53–86.Google Scholar
Metcalfe, R. W., Orszag, S. A., Brachet, M. E., Menon, S. & Riley, J. J. 1987 Secondary instability of a temporally growing mixing layer. J. Fluid Mech. 184, 207–243.Google Scholar
Monokrousos, A., Bottaro, A., Brandt, L., Di Vita, A. & Henningson, D. S. 2011 Nonequilibrium thermodynamics and the optimal path to turbulence in shear flows. Phys. Rev. Lett. 106, 134502.Google Scholar
Orr, W. M’F. 1907 The stability or instability of the steady motions of a perfect liquid and of a viscous liquid. Part I: a perfect liquid. Proc. R. Irish Acad. A 27, 9–68.Google Scholar
Ortiz, S. & Chomaz, J.-M. 2011 Transient growth of secondary instabilities in parallel wakes: anti lift-up mechanism and hyperbolic instability. Phys. Fluids 23 (11), 114106.CrossRefGoogle Scholar
Pierrehumbert, R. T. & Widnall, S. E. 1982 The two- and three-dimensional instabilities of a spatially periodic shear layer. J. Fluid Mech. 114, 59–82.Google Scholar
Potylitsin, P. G. & Peltier, W. R. 1998 Stratification effects on the stability of columnar vortices on the f-plane. J. Fluid Mech. 355, 45–79.Google Scholar
Pringle, C. C. T. & Kerswell, R. R. 2010 Using nonlinear transient growth to construct the minimal seed for shear flow turbulence. Phys. Rev. Lett. 105, 154502.Google Scholar
Pringle, C. C. T., Willis, A. P. & Kerswell, R. R. 2012 Minimal seeds for shear flow turbulence: using nonlinear transient growth to touch the edge of chaos. J. Fluid Mech. 703, 415–443.CrossRefGoogle Scholar
Rabin, S. M. E., Caulfield, C. P. & Kerswell, R. R. 2012 Triggering turbulence efficiently in plane Couette flow. J. Fluid Mech. 712, 244–272.Google Scholar
Rogers, M. M. & Moser, R. D. 1992 The three-dimensional evolution of a plane mixing layer: the Kelvin–Helmholtz rollup. J. Fluid Mech. 243, 183–226.Google Scholar
Schmid, P. J. 2007 Nonmodal stability theory. Annu. Rev. Fluid Mech. 39, 129–162.CrossRefGoogle Scholar
Schoppa, W., Hussain, F. & Metcalfe, R. W. 1995 A new mechanism of small-scale transition in a plane mixing layer: core dynamics of spanwise vortices. J. Fluid Mech. 298, 23–80.Google Scholar
Smyth, W. D. & Peltier, W. R. 1994 Three-dimensionalization of barotropic vortices on the f-plane. J. Fluid Mech. 265, 25–64.Google Scholar
Squire, H. B. 1933 On the stability of three-dimensional disturbances of viscous flow between parallel walls. Proc. R. Soc. Lond. A 142, 621–628.Google Scholar
Vitoshkin, H., Heifetz, E., Gelfgat, A. Yu. & Harnik, N. 2012 On the role of vortex stretching in energy optimal growth of three-dimensional perturbations on plane parallel shear flows. J. Fluid Mech. 707, 369–380.Google Scholar
Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids A 2, 76–80.Google Scholar
Winant, C. D. & Browand, F. K. 1974 Vortex pairing: the mechanism of turbulent mixing-layer growth at moderate Reynolds number. J. Fluid Mech. 63, 237–255.Google Scholar