Article contents
Transition to chaos through period doublings of a forced oscillating cylinder in steady current
Published online by Cambridge University Press: 21 January 2020
Abstract
Transition to chaos through a cascade of period doublings of the primary  $1/2$ synchronization mode is discovered in steady approaching flow around a forced inline oscillating cylinder near a plane boundary at a Reynolds number
$1/2$ synchronization mode is discovered in steady approaching flow around a forced inline oscillating cylinder near a plane boundary at a Reynolds number  $(Re)$ of 175. The transition occurs well within the otherwise synchronized region (known as the Arnold tongue) in the frequency and amplitude space of the oscillating cylinder, creating two parameter strips of desynchronized flows within the Arnold tongue. Five orders of period doublings from mode
$(Re)$ of 175. The transition occurs well within the otherwise synchronized region (known as the Arnold tongue) in the frequency and amplitude space of the oscillating cylinder, creating two parameter strips of desynchronized flows within the Arnold tongue. Five orders of period doublings from mode  $1/2$ to mode
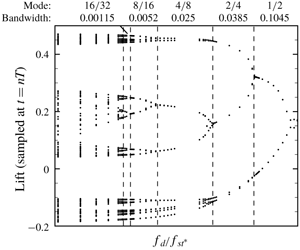
$1/2$ to mode  $16/32$ are revealed by progressively increasing the frequency resolution in the simulation. The ratio of frequency intervals of two successive period-doubling modes asymptotes towards the first Feigenbaum constant, reaching a value of 4.52 at mode of
$16/32$ are revealed by progressively increasing the frequency resolution in the simulation. The ratio of frequency intervals of two successive period-doubling modes asymptotes towards the first Feigenbaum constant, reaching a value of 4.52 at mode of  $16/32$. Additional three-dimensional simulations demonstrate the existence of period doubling with a regular spanwise flow structure similar to regular mode B of steady flow around an isolated cylinder. Although transition to chaos through cascades of period doublings is primarily reported for the primary
$16/32$. Additional three-dimensional simulations demonstrate the existence of period doubling with a regular spanwise flow structure similar to regular mode B of steady flow around an isolated cylinder. Although transition to chaos through cascades of period doublings is primarily reported for the primary  $1/2$ synchronization mode, it is also observed for other synchronization modes
$1/2$ synchronization mode, it is also observed for other synchronization modes  $(p/q)$ (Tang et al., J. Fluid Mech., vol. 832, 2017, pp. 146–169), where
$(p/q)$ (Tang et al., J. Fluid Mech., vol. 832, 2017, pp. 146–169), where  $p$ and
$p$ and  $q$ are integers with a non-reducible
$q$ are integers with a non-reducible  $p/q$, such as
$p/q$, such as  $2/3$. The physical mechanisms responsible for the present period-doubling bifurcations and transition to chaos through cascades of period doublings are ascribed to the interaction of asymmetric vortex shedding from the cylinder (due to a geometric asymmetry) and the boundary layer developed on the plane boundary, through specifically designed numerical tests.
$2/3$. The physical mechanisms responsible for the present period-doubling bifurcations and transition to chaos through cascades of period doublings are ascribed to the interaction of asymmetric vortex shedding from the cylinder (due to a geometric asymmetry) and the boundary layer developed on the plane boundary, through specifically designed numerical tests.
JFM classification
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2020. Published by Cambridge University Press
References
- 5
- Cited by

