Published online by Cambridge University Press: 18 October 2011
Incompressible flow in toroidal pipes of circular cross-section was investigated by three-dimensional, time-dependent numerical simulations using a finite volume method. The computational domain included a whole torus and was discretized by up to 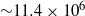 nodes. Two curvatures
nodes. Two curvatures 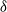 (radius of the cross-section/radius of the torus), namely 0.3 and 0.1, were examined; a streamwise forcing term was imposed, and its magnitude was made to vary so that the bulk Reynolds number ranged between
(radius of the cross-section/radius of the torus), namely 0.3 and 0.1, were examined; a streamwise forcing term was imposed, and its magnitude was made to vary so that the bulk Reynolds number ranged between 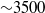 and
and 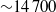 . The results were processed by different techniques in order to confirm the spatio-temporal structure of the flow. Consecutive transitions between different flow regimes were found, from stationary to periodic, quasi-periodic and chaotic flow. At low Reynolds number, stationary flow was predicted, exhibiting a symmetric couple of Dean vortex rings and a strong shift of the streamwise velocity maximum towards the outer wall. For
. The results were processed by different techniques in order to confirm the spatio-temporal structure of the flow. Consecutive transitions between different flow regimes were found, from stationary to periodic, quasi-periodic and chaotic flow. At low Reynolds number, stationary flow was predicted, exhibiting a symmetric couple of Dean vortex rings and a strong shift of the streamwise velocity maximum towards the outer wall. For 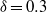 , between
, between 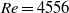 and
and 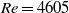 a first transition occurred from stationary to periodic flow, associated with a supercritical Hopf bifurcation and giving rise to a travelling wave which took the form of a varicose streamwise modulation of the Dean vortex ring intensity. A further transition, associated with a secondary Hopf bifurcation, occurred between
a first transition occurred from stationary to periodic flow, associated with a supercritical Hopf bifurcation and giving rise to a travelling wave which took the form of a varicose streamwise modulation of the Dean vortex ring intensity. A further transition, associated with a secondary Hopf bifurcation, occurred between 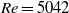 and
and 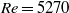 and led to a quasi-periodic flow characterized by two independent fundamental frequencies associated with distinct travelling waves, the first affecting mainly the Dean vortex rings and similar to that observed in purely periodic flow, the second localized mainly in the secondary flow boundary layers and manifesting itself as an array of oblique vortices produced at the edge of the Dean vortex regions. Both the periodic and the quasi-periodic regimes were characterized by an instantaneous anti-symmetry of the oscillatory components with respect to the equatorial midplane of the torus. For
and led to a quasi-periodic flow characterized by two independent fundamental frequencies associated with distinct travelling waves, the first affecting mainly the Dean vortex rings and similar to that observed in purely periodic flow, the second localized mainly in the secondary flow boundary layers and manifesting itself as an array of oblique vortices produced at the edge of the Dean vortex regions. Both the periodic and the quasi-periodic regimes were characterized by an instantaneous anti-symmetry of the oscillatory components with respect to the equatorial midplane of the torus. For 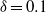 , between
, between 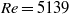 and
and 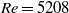 a direct (‘hard’) transition from steady to quasi-periodic flow occurred. Hysteresis was also observed: starting from a quasi-periodic solution and letting the Reynolds number decrease, both quasi-periodic and periodic stable solutions were obtained at Reynolds numbers below the critical value. A further decrease in
a direct (‘hard’) transition from steady to quasi-periodic flow occurred. Hysteresis was also observed: starting from a quasi-periodic solution and letting the Reynolds number decrease, both quasi-periodic and periodic stable solutions were obtained at Reynolds numbers below the critical value. A further decrease in 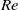 led to steady-state solutions. This behaviour suggests the existence of a subcritical Hopf bifurcation followed by a secondary Hopf bifurcation. The resulting periodic and quasi-periodic flows were similar to those observed for the higher curvature, but the travelling modes were now instantaneously symmetric with respect to the equatorial midplane of the torus. Also, the further transition from quasi-periodic to chaotic flow occurred with different modalities for the two curvatures. For
led to steady-state solutions. This behaviour suggests the existence of a subcritical Hopf bifurcation followed by a secondary Hopf bifurcation. The resulting periodic and quasi-periodic flows were similar to those observed for the higher curvature, but the travelling modes were now instantaneously symmetric with respect to the equatorial midplane of the torus. Also, the further transition from quasi-periodic to chaotic flow occurred with different modalities for the two curvatures. For 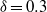 , a centrifugal instability of the main flow in the outer region occurred abruptly between
, a centrifugal instability of the main flow in the outer region occurred abruptly between 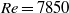 and
and 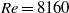 , while a further increase of
, while a further increase of 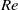 up to 13 180 did not cause any relevant change in the distribution and intensity of the fluctuations. For
up to 13 180 did not cause any relevant change in the distribution and intensity of the fluctuations. For  the transition to chaotic flow was gradual in the range
the transition to chaotic flow was gradual in the range 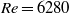 to 8160 and affected mainly the inner region; only a further increase of
to 8160 and affected mainly the inner region; only a further increase of 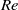 to 14 700 caused fluctuations to appear also in the outer region.
to 14 700 caused fluctuations to appear also in the outer region.
Current address: ENEA UTIS-TCI, C.R. Brasimone, 40032 Camugnano(Bo), Italy.