Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-29T11:33:45.706Z Has data issue: false hasContentIssue false
  • English
  • Français

Travelling vortices over mountains and the long-term structure of the residual flow

Published online by Cambridge University Press:  19 July 2021

Luis Zavala Sansón Open the ORCID record for Luis Zavala Sansón [Opens in a new window]  and
Jeasson F. Gonzalez Open the ORCID record for Jeasson F. Gonzalez [Opens in a new window]
Luis Zavala Sansón*
Affiliation:
Departamento de Oceanografía Física, CICESE, Carretera Ensenada-Tijuana 3918, 22860Ensenada, Baja California, México
Jeasson F. Gonzalez
Affiliation:
Departamento de Oceanografía Física, CICESE, Carretera Ensenada-Tijuana 3918, 22860Ensenada, Baja California, México
*
†Email address for correspondence: lzavala@cicese.mx
Get access Rights & Permissions [Opens in a new window]

Abstract

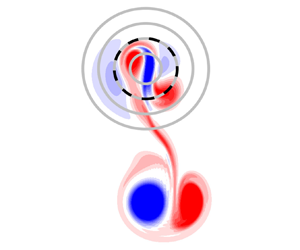
In the context of rotating geophysical flows, the presence of variable topography affects the motion of intense vortices and promotes the generation of new vortical structures. In this study, the quasi-two-dimensional dynamics of such systems is examined with numerical simulations and analytical models. The results are discussed from two points of view. First, the motion of a barotropic, dipolar vortex encountering a submarine mountain is analysed, with an emphasis on the modification of the trajectory and dipole structure when passing over the topography. For relatively low mountains, the vortex path is deflected towards the anticyclonic side of the dipole owing to squeezing effects (as the anticyclone becomes more intense than the cyclonic part). For higher mountains, the dipole splits into two parts; the anticyclone pairs with newly formed positive vorticity (generated by the stretching fluid moving downhill), while the cyclone remains trapped near the summit. These results are discussed using modulated point-vortex models. Second, the long-lived residual flows over the topography are studied. The most conspicuous cases are asymmetric dipolar vortices, which remain confined on the summit while rotating clockwise. The formation of new dipoles arises from the combination of nonlinear motions and topographic Rossby waves around the mountain. The results are illustrated with new analytical solutions of nonlinear dipoles over mountains.

JFM classification

Vortex Flows: Vortex dynamics Geophysical and Geological Flows: Topographic effects Geophysical and Geological Flows: Rotating flows
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 922 , 10 September 2021 , A33
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Aref, H. 1979 Motion of three vortices. Phys. Fluids 22 (3), 393–400.CrossRefGoogle Scholar
Aref, H. 2009 Stability of relative equilibria of three vortices. Phys. Fluids 21 (9), 094101.CrossRefGoogle Scholar
Beckmann, A. & Mohn, C. 2002 The upper ocean circulation at Great Meteor Seamount. Ocean Dyn. 52 (4), 194–204.CrossRefGoogle Scholar
Camassa, R., Holm, D.D. & Levermore, C.D. 1997 Long-time shallow-water equations with a varying bottom. J. Fluid Mech. 349, 173–189.CrossRefGoogle Scholar
Carnevale, G.F., Kloosterziel, R.C. & van Heijst, G.J.F. 1991 Propagation of barotropic vortices over topography in a rotating tank. J. Fluid Mech. 233, 119–139.CrossRefGoogle Scholar
Carnevale, G.F., Purini, R., Orlandi, P. & Cavazza, P. 1995 Barotropic quasi-geostrophic f-plane flow over anisotropic topography. J. Fluid Mech. 285, 329–347.CrossRefGoogle Scholar
Cenedese, C. 2002 Laboratory experiments on mesoscale vortices colliding with a seamount. J. Geophys. Res.: Oceans 107 (C6), 3053.CrossRefGoogle Scholar
Chapman, D.C. & Haidvogel, D.B. 1992 Formation of Taylor caps over a tall isolated seamount in a stratified ocean. Geophys. Astrophys. Fluid Dyn. 64 (1–4), 31–65.CrossRefGoogle Scholar
Flierl, G.R., Stern, M.E. & Whitehead, J.A. Jr. 1983 The physical significance of modons: laboratory experiments and general integral constraints. Dyn. Atmos. Oceans 7 (4), 233–263.CrossRefGoogle Scholar
Flór, J.-B. & Eames, I. 2002 Dynamics of monopolar vortices on a topographic beta-plane. J. Fluid Mech. 456, 353–376.CrossRefGoogle Scholar
van Geffen, J.H.G.M. & Davies, P.A. 2000 A monopolar vortex encounters an isolated topographic feature on a $\beta$-plane. Dyn. Atmos. Oceans 32 (1), 1–26.CrossRefGoogle Scholar
Genin, A. 2004 Bio-physical coupling in the formation of zooplankton and fish aggregations over abrupt topographies. J. Mar. Syst. 50 (1–2), 3–20.CrossRefGoogle Scholar
Gonzalez, J.F. & Zavala Sansón, L. 2021 Quasi-geostrophic vortex solutions over isolated topography. J. Fluid Mech. 915, A64.CrossRefGoogle Scholar
Grimshaw, R., Tang, Y. & Broutman, D. 1994 The effect of vortex stretching on the evolution of barotropic eddies over a topographic slope. Geophys. Astrophys. Fluid Dyn. 76 (1–4), 43–71.CrossRefGoogle Scholar
van Heijst, G.J.F. 1994 Topography effects on vortices in a rotating fluid. Meccanica 29 (4), 431–451.CrossRefGoogle Scholar
van Heijst, G.J.F. & Clercx, H.J.H. 2009 Laboratory modeling of geophysical vortices. Annu. Rev. Fluid Mech. 41, 143–164.CrossRefGoogle Scholar
Herbette, S., Morel, Y. & Arhan, M. 2005 Erosion of a surface vortex by a seamount on the $\beta$ plane. J. Phys. Oceanogr. 35 (11), 2012–2030.CrossRefGoogle Scholar
Hinds, A.K., Eames, I., Johnson, E.R. & McDonald, N.R. 2009 Laboratory study of vortex dipoles interacting with step topography. J. Geophys. Res.: Oceans 114 (C6), C06006.Google Scholar
Hinds, A.K., Johnson, E.R. & McDonald, N.R. 2016 Beach vortices near circular topography. Phys. Fluids 28 (10), 106602.CrossRefGoogle Scholar
Hopfinger, E.J. & van Heijst, G.J.F. 1993 Vortices in rotating fluids. Annu. Rev. Fluid Mech. 25 (1), 241–289.CrossRefGoogle Scholar
Hughes, C.W. & Miller, P.I. 2017 Rapid water transport by long-lasting modon eddy pairs in the southern midlatitude oceans. Geophys. Res. Lett. 44 (24), 12–375.CrossRefGoogle Scholar
Huppert, H.E. & Bryan, K. 1976 Topographically generated eddies. Deep-Sea Res. 23, 655–679.Google Scholar
Killworth, P.D. 1992 An equivalent-barotropic mode in the Fine Resolution Antarctic Model. J. Phys. Oceanogr. 22 (11), 1379–1387.2.0.CO;2>CrossRefGoogle Scholar
van Leeuwen, P.J. 2007 The propagation mechanism of a vortex on the $\beta$ plane. J. Phys. Oceanogr. 37 (9), 2316–2330.CrossRefGoogle Scholar
Meleshko, V.V. & van Heijst, G.J.F. 1994 On Chaplygin's investigations of two-dimensional vortex structures in an inviscid fluid. J. Fluid Mech. 272, 157–182.CrossRefGoogle Scholar
Nencioli, F., Dall'Olmo, G. & Quartly, G.D. 2018 Agulhas ring transport efficiency from combined satellite altimetry and Argo profiles. J. Geophys. Res.: Oceans 123 (8), 5874–5888.CrossRefGoogle Scholar
Nycander, J. & Lacasce, J.H. 2004 Stable and unstable vortices attached to seamounts. J. Fluid Mech. 507, 71–94.CrossRefGoogle Scholar
Orlandi, P. 1990 Vortex dipole rebound from a wall. Phys. Fluids A 2 (8), 1429–1436.CrossRefGoogle Scholar
Pedlosky, J. 1987 Geophysical Fluid Dynamics. Springer Science & Business Media.CrossRefGoogle Scholar
Rhines, P.B. 1969 Slow oscillations in an ocean of varying depth. Part 2. Islands and seamounts. J. Fluid Mech. 37 (1), 191–205.CrossRefGoogle Scholar
Ryzhov, E.A. & Koshel, K.V. 2013 Interaction of a monopole vortex with an isolated topographic feature in a three-layer geophysical flow. Nonlinear Process. Geophys. 20, 107–119.CrossRefGoogle Scholar
Schouten, M.W., de Ruijter, W.P.M., van Leeuwen, P.J. & Lutjeharms, J.R.E. 2000 Translation, decay and splitting of Agulhas rings in the southeastern Atlantic Ocean. J. Geophys. Res.: Oceans 105 (C9), 21913–21925.CrossRefGoogle Scholar
Sutyrin, G.G. & Grimshaw, R. 2010 The long-time interaction of an eddy with shelf topography. Ocean Model. 32 (1–2), 25–35.CrossRefGoogle Scholar
Taylor, G.I. 1921 Experiments with rotating fluids. Proc. R. Soc. Lond. A 100 (703), 114–121.Google Scholar
Tenreiro, M., Zavala Sansón, L. & van Heijst, G.J.F. 2006 Interaction of dipolar vortices with a step-like topography. Phys. Fluids 18 (5), 056603.CrossRefGoogle Scholar
Trasviña-Castro, A., de Velasco Gutiérrez, G., Valle-Levinson, A., Gonzalez-Armas, R., Muhlia, A. & Cosio, M.A. 2003 Hydrographic observations of the flow in the vicinity of a shallow seamount top in the Gulf of California. Estuar. Coast. Shelf Sci. 57 (1–2), 149–162.CrossRefGoogle Scholar
Vallis, G.K. 2017 Atmospheric and Oceanic Fluid Dynamics. Cambridge University Press.CrossRefGoogle Scholar
Verron, J. & Le Provost, C. 1985 A numerical study of quasi-geostrophic flow over isolated topography. J. Fluid Mech. 154, 231–252.CrossRefGoogle Scholar
Verzicco, R., Flór, J.B., van Heijst, G.J.F. & Orlandi, P. 1995 Numerical and experimental study of the interaction between a vortex dipole and a circular cylinder. Exp. Fluids 18 (3), 153–163.CrossRefGoogle Scholar
Viúdez, A. 2019 Azimuthal-mode solutions of two-dimensional Euler flows and the Chaplygin–Lamb dipole. J. Fluid Mech. 859, R1.CrossRefGoogle Scholar
Zabusky, N.J. & McWilliams, J.C. 1982 A modulated point-vortex model for geostrophic, $\beta$-plane dynamics. Phys. Fluids 25 (12), 2175–2182.CrossRefGoogle Scholar
Zavala Sansón, L. 2002 Vortex–ridge interaction in a rotating fluid. Dyn. Atmos. Oceans 35 (4), 299–325.CrossRefGoogle Scholar
Zavala Sansón, L. 2010 Solutions of barotropic trapped waves around seamounts. J. Fluid Mech. 661, 32–44.CrossRefGoogle Scholar
Zavala Sansón, L. 2019 Nonlinear and time-dependent equivalent-barotropic flows. J. Fluid Mech. 871, 925–951.CrossRefGoogle Scholar
Zavala Sansón, L., Barbosa Aguiar, A.C. & van Heijst, G.J.F. 2012 Horizontal and vertical motions of barotropic vortices over a submarine mountain. J. Fluid Mech. 695, 173–198.CrossRefGoogle Scholar
Zavala Sansón, L. & van Heijst, G.J.F. 2000 Interaction of barotropic vortices with coastal topography: laboratory experiments and numerical simulations. J. Phys. Oceanogr. 30 (9), 2141–2162.2.0.CO;2>CrossRefGoogle Scholar
Zavala Sansón, L. & van Heijst, G.J.F. 2002 Ekman effects in a rotating flow over bottom topography. J. Fluid Mech. 471, 239–255.CrossRefGoogle Scholar
Zavala Sansón, L. & van Heijst, G.J.F. 2014 Laboratory experiments on flows over bottom topography. In Modeling Atmospheric and Oceanic Flows: Insights from Laboratory Experiments and Numerical Simulations (ed. T. von Larcher & P.D. Williams). Wiley.CrossRefGoogle Scholar
Zavala Sansón, L., van Heijst, G.J.F. & Backx, N.A. 2001 Ekman decay of a dipolar vortex in a rotating fluid. Phys. Fluids 13 (2), 440–451.CrossRefGoogle Scholar
Zavala Sansón, L., van Heijst, G.J.F. & Doorschot, J.J.J. 1999 Reflection of barotropic vortices from a step-like topography. Il Nuovo Cimento 22 (6), 909–930.Google Scholar
Zhao, B., Chieusse-Gérard, E. & Flierl, G. 2019 Influence of bottom topography on vortex stability. J. Phys. Oceanogr. 49 (12), 3199–3219.CrossRefGoogle Scholar

Zavala Sansón and Gonzalez supplementary movie 1

Evolution of the relative vorticity of a dipolar vortex encountering a narrow mountain (simulation B_21 in Table 1). A strong interaction is verified during the first 15 days. A new dipole rotating in the clock-wise direction over the mountain is formed at longer times (from day 30 and onwards).

Download Zavala Sansón and Gonzalez supplementary movie 1(Video)
Video 1 MB

Zavala Sansón and Gonzalez supplementary movie 2

Evolution of the relative vorticity of a dipolar vortex encountering a wide mountain (simulation A_23 in Table 1). The interaction is weak during the first 15 days. The convoluted patterns at later times result from the generation of dispersive topographic Rossby waves over the mountain slope, which travel with shallow water to the right.

Download Zavala Sansón and Gonzalez supplementary movie 2(Video)
Video 1.3 MB