Published online by Cambridge University Press: 21 March 2014
Direct numerical simulations are employed to investigate the interactions of bidisperse turbidity currents with three-dimensional seafloor topography in the form of Gaussian bumps. Results for two different bump heights are compared against currents propagating over a flat surface. The bump heights are chosen such that the current largely flows over the smaller bump, while it primarily flows around the taller bump. Furthermore, the effects of the settling velocity are investigated by comparing turbidity currents with corresponding compositional gravity currents. The influence of the bottom topography on the front velocity of turbidity currents is seen to be much weaker than the influence of the particle settling velocity. Consistent with earlier work on gravity currents propagating over flat boundaries, the influence of the Reynolds number on the front velocity of currents interacting with three-dimensional bottom topography is found to be small, as long as 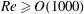 $\mathit{Re}\geq O(1000)$. The lobe-and-cleft structures, on the other hand, exhibit a stronger influence of the Reynolds number. The current/bump interaction deforms the bottom boundary-layer vorticity into traditional horseshoe vortices, with a downwash region in the centre of the wake. At the same time, the vorticity originating in the mixing layer between the current and the ambient interacts with the bump in such a way as to form ‘inverted horseshoe vortices’, with an upwash region in the wake centre. Additional streamwise vortical structures form as a result of baroclinic vorticity generation. The dependence of the sedimentation rate and streamwise vorticity generation on the height of the bump are discussed, and detailed analyses are presented of the energy budget and bottom wall-shear stress. It is shown that for typical laboratory-scale experiments, the range of parameters explored in the present investigation will not give rise to bedload transport or sediment resuspension. Based on balance arguments for the kinetic and potential energy components, a scaling law is obtained for the maximum bump height over which gravity currents can travel. This scaling law is validated by simulation results, and it provides a criterion for distinguishing between ‘short’ and ‘tall’ topographical features. For turbidity currents, this scaling result represents an upper limit. An interesting non-monotonic influence of the bump height is observed on the long-term propagation velocity of the current. On the one hand, the lateral deflection of the current by the bump leads to an effective increase in the current height and its front velocity in the region away from the bump. At the same time, taller bumps result in a more vigorous three-dimensional evolution of the current, accompanied by increased levels of dissipation, which slows the current down. For small bumps, the former mechanism dominates, so that on average the current front propagates faster than its flat bottom counterpart. For currents interacting with larger bumps, however, the increased dissipation becomes dominant, so that they exhibit a reduced front velocity as compared to currents propagating over flat surfaces.
$\mathit{Re}\geq O(1000)$. The lobe-and-cleft structures, on the other hand, exhibit a stronger influence of the Reynolds number. The current/bump interaction deforms the bottom boundary-layer vorticity into traditional horseshoe vortices, with a downwash region in the centre of the wake. At the same time, the vorticity originating in the mixing layer between the current and the ambient interacts with the bump in such a way as to form ‘inverted horseshoe vortices’, with an upwash region in the wake centre. Additional streamwise vortical structures form as a result of baroclinic vorticity generation. The dependence of the sedimentation rate and streamwise vorticity generation on the height of the bump are discussed, and detailed analyses are presented of the energy budget and bottom wall-shear stress. It is shown that for typical laboratory-scale experiments, the range of parameters explored in the present investigation will not give rise to bedload transport or sediment resuspension. Based on balance arguments for the kinetic and potential energy components, a scaling law is obtained for the maximum bump height over which gravity currents can travel. This scaling law is validated by simulation results, and it provides a criterion for distinguishing between ‘short’ and ‘tall’ topographical features. For turbidity currents, this scaling result represents an upper limit. An interesting non-monotonic influence of the bump height is observed on the long-term propagation velocity of the current. On the one hand, the lateral deflection of the current by the bump leads to an effective increase in the current height and its front velocity in the region away from the bump. At the same time, taller bumps result in a more vigorous three-dimensional evolution of the current, accompanied by increased levels of dissipation, which slows the current down. For small bumps, the former mechanism dominates, so that on average the current front propagates faster than its flat bottom counterpart. For currents interacting with larger bumps, however, the increased dissipation becomes dominant, so that they exhibit a reduced front velocity as compared to currents propagating over flat surfaces.