Article contents
Turbulence induced by a swarm of rising bubbles from coarse-grained simulations
Published online by Cambridge University Press: 12 April 2024
Abstract
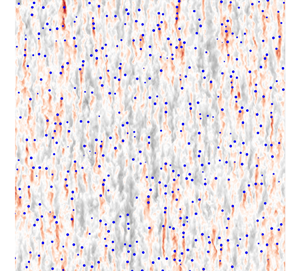
We performed numerical simulations of a homogeneous swarm of bubbles rising at large Reynolds number,  $Re=760$, with volume fractions ranging from 1 % to 10 %. We consider a simplified model in which the interfaces are not resolved, but which allows us to simulate flows with a large number of bubbles and to emphasize the interactions between bubble wakes. The liquid phase is described by solving, on an Eulerian grid, the Navier–Stokes equations, including sources of momentum which model the effect of the bubbles. The dynamics of each bubble is determined within the Lagrangian framework by solving an equation of motion involving the hydrodynamic forces exerted by the fluid accounting for the correction of the fictitious self-interaction of a bubble with its own wake. The comparison with experiments shows that this coarse-grained simulations approach can reliably describe the dynamics of the resolved flow scales. We use conditional averaging to characterize the mean bubble wakes and obtain in particular the typical shear imposed by the rising bubbles. On the basis of the spectral decomposition of the energy budget, we observe that the flow is dominated by production at large scales and by dissipation at small scales and we rule out the presence of an intermediate range in which the production and dissipation are locally in balance. We propose that the
$Re=760$, with volume fractions ranging from 1 % to 10 %. We consider a simplified model in which the interfaces are not resolved, but which allows us to simulate flows with a large number of bubbles and to emphasize the interactions between bubble wakes. The liquid phase is described by solving, on an Eulerian grid, the Navier–Stokes equations, including sources of momentum which model the effect of the bubbles. The dynamics of each bubble is determined within the Lagrangian framework by solving an equation of motion involving the hydrodynamic forces exerted by the fluid accounting for the correction of the fictitious self-interaction of a bubble with its own wake. The comparison with experiments shows that this coarse-grained simulations approach can reliably describe the dynamics of the resolved flow scales. We use conditional averaging to characterize the mean bubble wakes and obtain in particular the typical shear imposed by the rising bubbles. On the basis of the spectral decomposition of the energy budget, we observe that the flow is dominated by production at large scales and by dissipation at small scales and we rule out the presence of an intermediate range in which the production and dissipation are locally in balance. We propose that the  $k^{-3}$ subrange of the energy spectra results from the mean shear rate imposed by the bubbles, which controls the rate of return to isotropy.
$k^{-3}$ subrange of the energy spectra results from the mean shear rate imposed by the bubbles, which controls the rate of return to isotropy.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2024. Published by Cambridge University Press
Footnotes
Present address: Institute of Meteorology and Climate Research, Institute for Hydromechanics, Karlsruhe Institute of Technology, Germany.
References
Zamansky et al. supplementary movie 1
Zamansky et al. supplementary movie 2
Zamansky et al. supplementary movie 3
- 9
- Cited by


