Hostname: page-component-78c5997874-s2hrs Total loading time: 0 Render date: 2024-11-13T01:25:03.221Z Has data issue: false hasContentIssue false
  • English
  • Français

The turbulent bubble break-up cascade. Part 1. Theoretical developments

Published online by Cambridge University Press:  15 February 2021

Wai Hong Ronald Chan Open the ORCID record for Wai Hong Ronald Chan [Opens in a new window] ,
Perry L. Johnson Open the ORCID record for Perry L. Johnson [Opens in a new window]  and
Parviz Moin Open the ORCID record for Parviz Moin [Opens in a new window]
Wai Hong Ronald Chan
Affiliation:
Center for Turbulence Research (CTR), Stanford University, Stanford, CA94305, USA
Perry L. Johnson
Affiliation:
Center for Turbulence Research (CTR), Stanford University, Stanford, CA94305, USA The Henry Samueli School of Engineering, University of California, Irvine, Irvine, CA92697, USA
Parviz Moin*
Affiliation:
Center for Turbulence Research (CTR), Stanford University, Stanford, CA94305, USA
*
†Email address for correspondence: moin@stanford.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

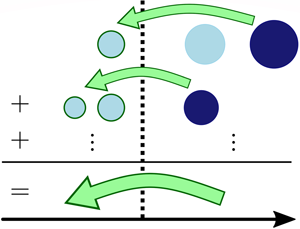
Breaking waves entrain gas beneath the surface. The wave-breaking process energizes turbulent fluctuations that break bubbles in quick succession to generate a wide range of bubble sizes. Understanding this generation mechanism paves the way towards the development of predictive models for large-scale maritime and climate simulations. Garrett et al. (J. Phys. Oceanogr., vol. 30, 2000, pp. 2163–2171) suggested that super-Hinze-scale turbulent break-up transfers entrained gas from large- to small-bubble sizes in the manner of a cascade. We provide a theoretical basis for this bubble-mass cascade by appealing to how energy is transferred from large to small scales in the energy cascade central to single-phase turbulence theories. A bubble break-up cascade requires that break-up events predominantly transfer bubble mass from a certain bubble size to a slightly smaller size on average. This property is called locality. In this paper, we analytically quantify locality by extending the population balance equation in conservative form to derive the bubble-mass-transfer rate from large to small sizes. Using our proposed measures of locality, we show that scalings relevant to turbulent bubbly flows, including those postulated by Garrett et al. (J. Phys. Oceanogr., vol. 30, 2000, pp. 2163–2171) and observed in breaking-wave experiments and simulations, are consistent with a strongly local transfer rate, where the influence of non-local contributions decays in a power-law fashion. These theoretical predictions are confirmed using numerical simulations in Part 2 (Chan et al., J. Fluid. Mech. vol. 912, 2021, A43), revealing key physical aspects of the bubble break-up cascade phenomenology. Locality supports the universality of turbulent small-bubble break-up, which simplifies the development of cascade-based subgrid-scale models to predict oceanic small-bubble statistics of practical importance.

JFM classification

Drops and Bubbles: Breakup/coalescence Multiphase and Particle-laden Flows: Gas/liquid flow Turbulent Flows: Turbulence theory
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 912 , 10 April 2021 , A42
Check for updates
Copyright
© The Author(s), 2021. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abramowitz, M. & Stegun, I.A. 1964 Handbook of Mathematical Functions. National Bureau of Standards, U.S. Department of Commerce.Google Scholar
Aluie, H. & Eyink, G.L. 2009 Localness of energy cascade in hydrodynamic turbulence. II. Sharp spectral filter. Phys. Fluids 21, 115108.CrossRefGoogle Scholar
Apte, S.V., Gorokhovski, M. & Moin, P. 2003 LES of atomizing spray with stochastic modeling of secondary breakup. Intl J. Multiphase Flow 29, 1503–1522.CrossRefGoogle Scholar
Batchelor, G.K. 1953 The Theory of Homogeneous Turbulence. Cambridge University Press.Google Scholar
Behnken, D.W., Horowitz, J. & Katz, S. 1963 Particle growth processes. Ind. Engng Chem. Fundam. 2 (3), 213–216.CrossRefGoogle Scholar
Blanchard, D.C. & Woodcock, A.H. 1957 Bubble formation and modification in the sea and its meteorological significance. Tellus 9, 145–158.CrossRefGoogle Scholar
Blenkinsopp, C.E. & Chaplin, J.R. 2010 Bubble size measurements in breaking waves using optical fiber phase detection probes. IEEE J. Ocean Engng 35, 388–401.CrossRefGoogle Scholar
Carrica, P.M., Drew, D., Bonetto, F. & Lahey, R.T. Jr. 1999 A polydisperse model for bubbly two-phase flow around a surface ship. Intl J. Multiphase Flow 25, 257–305.CrossRefGoogle Scholar
Castro, A.M. & Carrica, P.M. 2013 Bubble size distribution prediction for large-scale ship flows: model evaluation and numerical issues. Intl J. Multiphase Flow 57, 131–150.CrossRefGoogle Scholar
Chan, W.H.R., Dodd, M.S., Johnson, P.L., Urzay, J. & Moin, P. 2018 a Formation and dynamics of bubbles generated in breaking waves: Part II. The evolution of the bubble-size distribution and breakup/coalescence statistics. In Center for Turbulence Research Annual Research Briefs, Stanford University (ed. P. Moin & J. Urzay), pp. 21–34.Google Scholar
Chan, W.H.R. & Johnson, P.L. 2019 Locality in the turbulent bubble breakup cascade. In Center for Turbulence Research Annual Research Briefs, Stanford University (ed. P. Moin, A. Lozano-Durán & P. Johnson), pp. 121–136.Google Scholar
Chan, W.H.R., Johnson, P.L., Moin, P. & Urzay, J. 2021 The turbulent bubble breakup cascade. Part 2. Numerical simulations of breaking waves. J. Fluid Mech. 912, A43.Google Scholar
Chan, W.H.R., Mirjalili, S., Jain, S.S., Urzay, J., Mani, A. & Moin, P. 2019 Birth of microbubbles in turbulent breaking waves. Phys. Rev. Fluids 4, 100508.CrossRefGoogle Scholar
Chan, W.H.R., Urzay, J. & Moin, P. 2018 b Subgrid-scale modeling for microbubble generation amid colliding water surfaces. In Proceedings of the 32nd Symposium on Naval Hydrodynamics, arXiv:1811.11898.Google Scholar
Coulaloglou, C.A. & Tavlarides, L.L. 1977 Description of interaction processes in agitated liquid–liquid dispersions. Chem. Engng Sci. 32, 1289–1297.CrossRefGoogle Scholar
Deane, G.B. & Stokes, M.D. 2002 Scale dependence of bubble creation mechanisms in breaking waves. Nature 418, 839–844.CrossRefGoogle ScholarPubMed
Deike, L., Melville, W.K. & Popinet, S. 2016 Air entrainment and bubble statistics in breaking waves. J. Fluid Mech. 801, 91–129.CrossRefGoogle Scholar
Eyink, G.L. 2005 Locality of turbulent cascades. Physica D 207, 91–116.CrossRefGoogle Scholar
Eyink, G.L. & Aluie, H. 2009 Localness of energy cascade in hydrodynamic turbulence. I. Smooth coarse graining. Phys. Fluids 21, 115107.CrossRefGoogle Scholar
Filippov, A.F. 1961 On the distribution of the sizes of particles which undergo splitting. Theory Prob. Applics. 6, 275–294.CrossRefGoogle Scholar
Fredrickson, A.G. & Tsuchiya, H.M. 1963 Continuous propagation of microorganisms. AIChE J. 9 (4), 459–468.CrossRefGoogle Scholar
Friedlander, S.K. 1960 a On the particle-size spectrum of atmospheric aerosols. J. Meteorol. 17 (3), 373–374.2.0.CO;2>CrossRefGoogle Scholar
Friedlander, S.K. 1960 b Similarity considerations for the particle-size spectrum of a coagulating, sedimenting aerosol. J. Meteorol. 17 (5), 479–483.2.0.CO;2>CrossRefGoogle Scholar
Garrett, C., Li, M. & Farmer, D. 2000 The connection between bubble size spectra and energy dissipation rates in the upper ocean. J. Phys. Oceanogr. 30, 2163–2171.2.0.CO;2>CrossRefGoogle Scholar
Garrettson, G.A. 1973 Bubble transport theory with application to the upper ocean. J. Fluid Mech. 59, 187–206.CrossRefGoogle Scholar
Heisenberg, W. 1948 a On the theory of statistical and isotropic turbulence. Proc. R. Soc. Lond. A 195 (1042), 402–406.Google Scholar
Heisenberg, W. 1948 b Zur statistischen theorie der turbulenz. Z. Phys. 124, 628–657.CrossRefGoogle Scholar
Hinze, J.O. 1955 Fundamentals of the hydrodynamic mechanism of splitting in dispersion processes. AIChE J. 1, 289–295.CrossRefGoogle Scholar
Hulburt, H.M. & Katz, S. 1964 Some problems in particle technology: a statistical mechanical formulation. Chem. Engng Sci. 19, 555–574.CrossRefGoogle Scholar
Kiger, K.T. & Duncan, J.H. 2012 Air-entrainment mechanisms in plunging jets and breaking waves. Annu. Rev. Fluid Mech. 44, 563–596.CrossRefGoogle Scholar
Kolmogorov, A.N. 1941 The local structure of turbulence in incompressible viscous fluid for very large Reynolds numbers. Dokl. Akad. Nauk SSSR 30, 299–303.Google Scholar
Kolmogorov, A.N. 1949 On the breakage of drops in a turbulent flow. Dokl. Akad. Nauk SSSR 66, 825–828.Google Scholar
Kovasznay, L.S.G. 1948 Spectrum of locally isotropic turbulence. J. Aeronaut. Sci. 15 (12), 745–753.CrossRefGoogle Scholar
Kraichnan, R.H. 1971 Inertial-range transfer in two- and three-dimensional turbulence. J. Fluid Mech. 47, 525–535.CrossRefGoogle Scholar
Landau, L. & Rumer, G. 1938 The cascade theory of electronic showers. Proc. R. Soc. Lond. A 166, 213–228.Google Scholar
Lasheras, J.C., Eastwood, C., Martínez-Bazán, C. & Montañés, J.L. 2002 A review of statistical models for the break-up of an immiscible fluid immersed into a fully developed turbulent flow. Intl J. Multiphase Flow 28, 247–278.CrossRefGoogle Scholar
Lee, C.-H., Erickson, L.E. & Glasgow, L.A. 1987 a Bubble breakup and coalescence in turbulent gas–liquid dispersions. Chem. Engng Commun. 59, 65–84.CrossRefGoogle Scholar
Lee, C.-H., Erickson, L.E. & Glasgow, L.A. 1987 b Dynamics of bubble-size distribution in turbulent gas–liquid dispersions. Chem. Engng Commun. 61, 181–195.CrossRefGoogle Scholar
Liao, Y. & Lucas, D. 2009 A literature review of theoretical models for drop and bubble breakup in turbulent dispersions. Chem. Engng Sci. 64, 3389–3406.CrossRefGoogle Scholar
Loewen, M.R., O'Dor, M.A. & Skafel, M.G. 1996 Bubbles generated by mechanically generated breaking waves. J. Geophys. Res. Oceans 101 (C9), 20759–20769.CrossRefGoogle Scholar
Luo, H. & Svendsen, H.F. 1996 Theoretical model for drop and bubble breakup in turbulent dispersions. AIChE J. 42, 1225–1233.CrossRefGoogle Scholar
L'vov, V. & Falkovich, G. 1992 Counterbalanced interaction locality of developed hydrodynamic turbulence. Phys. Rev. A 46 (8), 4762–4772.CrossRefGoogle ScholarPubMed
Martínez-Bazán, C., Montañés, J.L. & Lasheras, J.C. 1999 a On the breakup of an air bubble injected into a fully developed turbulent flow. Part 1. Breakup frequency. J. Fluid Mech. 401, 157–182.CrossRefGoogle Scholar
Martínez-Bazán, C., Montañés, J.L. & Lasheras, J.C. 1999b On the breakup of an air bubble injected into a fully developed turbulent flow. Part 2. Size PDF of the resulting daughter bubbles. J. Fluid Mech. 401, 183–207.CrossRefGoogle Scholar
Martínez-Bazán, C., Rodríguez-Rodríguez, J., Deane, G.B., Montañes, J.L. & Lasheras, J.C. 2010 Considerations on bubble fragmentation models. J. Fluid Mech. 661, 159–177.CrossRefGoogle Scholar
Masnadi, N., Erinin, M.A., Washuta, N., Nasiri, F., Balaras, E. & Duncan, J.H. 2020 Air entrainment and surface fluctuations in a turbulent ship hull boundary layer. J. Ship Res. 64 (2), 185–201.CrossRefGoogle Scholar
Medwin, H. 1970 In situ acoustic measurements of bubble populations in coastal ocean waters. J. Geophys. Res. 75 (3), 599–611.CrossRefGoogle Scholar
Melville, W.K. 1996 The role of surface-wave breaking in air-sea interaction. Annu. Rev. Fluid Mech. 28, 279–321.CrossRefGoogle Scholar
Melzak, Z.A. 1953 The effect of coalescence in certain collision processes. Q. Appl. Maths 11 (2), 231–234.CrossRefGoogle Scholar
Mirjalili, S., Chan, W.H.R. & Mani, A. 2018 High fidelity simulations of micro-bubble shedding from retracting thin gas films in the context of liquid-liquid impact. In Proceedings of the 32nd Symposium on Naval Hydrodynamics, arXiv:1811.12352.Google Scholar
Mirjalili, S. & Mani, A. 2020 Transitional stages of thin air film entrapment in drop-pool impact events. J. Fluid Mech. 901, A14.CrossRefGoogle Scholar
Mortazavi, M. 2016 Air entrainment and micro-bubble generation by turbulent breaking waves. PhD thesis, Stanford University.Google Scholar
Mortazavi, M., Le Chenadec, V., Moin, P. & Mani, A. 2016 Direct numerical simulation of a turbulent hydraulic jump: turbulence statistics and air entrainment. J. Fluid Mech. 797, 60–94.CrossRefGoogle Scholar
Na, B., Chang, K.-A., Huang, Z.-C. & Lim, H.-J. 2016 Turbulent flow field and air entrainment in laboratory plunging breaking waves. J. Geophys. Res. Oceans 121, 2980–3009.CrossRefGoogle Scholar
Narsimhan, G., Gupta, J.P. & Ramkrishna, D. 1979 A model for transitional breakage probability of droplets in agitated lean liquid–liquid dispersions. Chem. Engng Sci. 34, 257–265.CrossRefGoogle Scholar
Obukhov, A.M. 1941 Spectral energy distribution in a turbulent flow. Dokl. Akad. Nauk SSSR 32 (1), 22–24.Google Scholar
Onsager, L. 1945 The distribution of energy in turbulence. Phys. Rev. 68 (11–12), 286.Google Scholar
Pao, Y.-H. 1965 Structure of turbulent velocity and scalar fields at large wavenumbers. Phys. Fluids 8, 1063–1075.CrossRefGoogle Scholar
Pao, Y.-H. 1968 Transfer of turbulent energy and scalar quantities at large wavenumbers. Phys. Fluids 11, 1371–1372.CrossRefGoogle Scholar
Pope, S.B. 2000 Turbulent Flows. Cambridge University Press.CrossRefGoogle Scholar
Qi, Y., Masuk, A.U.M. & Ni, R. 2020 Towards a model of bubble breakup in turbulence through experimental constraints. Intl J. Multiphase Flow 132, 103397.CrossRefGoogle Scholar
Ramkrishna, D. 1985 The status of population balances. Rev. Chem. Engng 3, 49–95.Google Scholar
Randolph, A.D. 1964 A population balance for countable entities. Can. J. Chem. Engng 42 (6), 280–281.CrossRefGoogle Scholar
Randolph, A.D. & Larson, M.A. 1962 Transient and steady state size distributions in continuous mixed suspension crystallizers. AIChE J. 8 (5), 639–645.CrossRefGoogle Scholar
Richardson, L.F. 1922 Weather Prediction by Numerical Process. Cambridge University Press.Google Scholar
Rodríguez-Rodríguez, J., Gordillo, J.M. & Martínez-Bazán, C. 2006 Breakup time and morphology of drops and bubbles in a high-Reynolds-number flow. J. Fluid Mech. 548, 69–86.CrossRefGoogle Scholar
Rogallo, R.S. & Moin, P. 1984 Numerical simulation of turbulent flows. Annu. Rev. Fluid Mech. 16, 99–137.CrossRefGoogle Scholar
Rojas, G. & Loewen, M.R. 2007 Fiber-optic probe measurements of void fraction and bubble-size distributions beneath breaking waves. Exp. Fluids 43, 895–906.CrossRefGoogle Scholar
Saveliev, V.L. & Gorokhovski, M.A. 2012 Renormalization of the fragmentation equation: exact self-similar solutions and turbulent cascades. Phys. Rev. E 86, 061112.CrossRefGoogle ScholarPubMed
Shinnar, R. 1961 On the behaviour of liquid dispersions in mixing vessels. J. Fluid Mech. 10, 259–275.CrossRefGoogle Scholar
Smoluchowski, M.V. 1916 Drei vorträge über diffusion, brownsche molekularbewegung und koagulation von kolloidteilchen. Phys. Z. 17, 557–571.Google Scholar
Smoluchowski, M.V. 1918 Versuch einer mathematischen theorie der koagulationskinetik kolloider lẅosungen. Z. Phys. Chem. 92, 129–168.Google Scholar
Solsvik, J. & Jakobsen, H.A. 2015 The foundation of the population balance equation: a review. J. Disper. Sci. Technol. 36, 510–520.CrossRefGoogle Scholar
Solsvik, J., Tangen, S. & Jakobsen, H.A. 2013 On the constitutive equations for fluid particle breakage. Rev. Chem. Engng 29 (5), 241–356.Google Scholar
Tavakolinejad, M. 2010 Air bubble entrainment by breaking bow waves simulated by a ${2\textrm {D}+\textrm {T}}$ technique. PhD thesis, University of Maryland, College Park.Google Scholar
Thiesset, F., Duret, B., Ménard, T., Dumouchel, C., Reveillon, J. & Demoulin, F.X. 2020 Liquid transport in scale space. J. Fluid Mech. 886, A4.CrossRefGoogle Scholar
Thorpe, S.A. 1982 On the clouds of bubbles formed by breaking wind-waves in deep water, and their role in air-sea gas transfer. Phil. Trans. R. Soc. Lond. A 304, 155–210.Google Scholar
Thorpe, S.A. 1992 Bubble clouds and the dynamics of the upper ocean. Q. J. R. Meteorol. Soc. 118, 1–22.CrossRefGoogle Scholar
Trevorrow, M.V., Vagle, S. & Farmer, D.M. 1994 Acoustical measurements of microbubbles within ship wakes. J. Acoust. Soc. Am. 95, 1922–1930.CrossRefGoogle Scholar
Tsouris, C. & Tavlarides, L.L. 1994 Breakage and coalescence models for drops in turbulent dispersions. AIChE J. 40, 395–406.CrossRefGoogle Scholar
Valentas, K.J. & Amundson, N.R. 1966 Breakage and coalescence in dispersed phase systems. Ind. Engng Chem. Fundam. 5 (4), 533–542.CrossRefGoogle Scholar
Valentas, K.J., Bilous, O. & Amundson, N.R. 1966 Analysis of breakage in dispersed phase systems. Ind. Engng Chem. Fundam. 5 (2), 271–279.CrossRefGoogle Scholar
Wang, T., Wang, J. & Jin, Y. 2003 A novel theoretical breakup kernel function for bubbles/droplets in a turbulent flow. Chem. Engng Sci. 58, 4629–4637.CrossRefGoogle Scholar
Wang, Z., Yang, J. & Stern, F. 2016 High-fidelity simulations of bubble, droplet and spray formation in breaking waves. J. Fluid Mech. 792, 307–327.CrossRefGoogle Scholar
Williams, F.A. 1958 Spray combustion and atomization. Phys. Fluids 1, 541–545.CrossRefGoogle Scholar
Yu, X., Hendrickson, K., Campbell, B.K. & Yue, D.K.P. 2019 Numerical investigation of shear-flow free-surface turbulence and air entrainment at large Froude and Weber numbers. J. Fluid Mech. 880, 209–238.CrossRefGoogle Scholar
Yu, X., Hendrickson, K. & Yue, D.K.P. 2020 Scale separation and dependence of entrainment bubble-size distribution in free-surface turbulence. J. Fluid Mech. 885, R2.CrossRefGoogle Scholar
Zhou, Y. 1993 a Degrees of locality of energy transfer in the inertial range. Phys. Fluids A 5, 1092–1094.CrossRefGoogle Scholar
Zhou, Y. 1993 b Interacting scales and energy transfer in isotropic turbulence. Phys. Fluids A 5, 2511–2524.CrossRefGoogle Scholar