Hostname: page-component-cd9895bd7-gvvz8 Total loading time: 0 Render date: 2024-12-29T12:51:52.711Z Has data issue: false hasContentIssue false
  • English
  • Français

Turbulent mixing driven by spherical implosions. Part 1. Flow description and mixing-layer growth

Published online by Cambridge University Press:  28 April 2014

M. Lombardini ,
D. I. Pullin  and
D. I. Meiron
M. Lombardini*
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
D. I. Pullin
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
D. I. Meiron
Affiliation:
Graduate Aerospace Laboratories, California Institute of Technology, Pasadena, CA 91125, USA
*
†Email address for correspondence: manuel@caltech.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

We present large-eddy simulations (LES) of turbulent mixing at a perturbed, spherical interface separating two fluids of differing densities and subsequently impacted by a spherically imploding shock wave. This paper focuses on the differences between two fundamental configurations, keeping fixed the initial shock Mach number 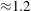${\approx }1.2$, the density ratio (precisely 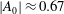$|A_0|\approx 0.67$) and the perturbation shape (dominant spherical wavenumber 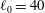$\ell _0=40$ and amplitude-to-initial radius of 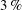$3\, \%$): the incident shock travels from the lighter fluid to the heavy fluid or, inversely, from the heavy to the light fluid. After describing the computational problem we present results on the radially symmetric flow, the mean flow, and the growth of the mixing layer. Turbulent statistics are developed in Part 2 (Lombardini, M., Pullin, D. I. & Meiron, D. I. J. Fluid Mech., vol. 748, 2014, pp. 113–142). A wave-diagram analysis of the radially symmetric flow highlights that the light–heavy mixing layer is processed by consecutive reshocks, and not by reverberating rarefaction waves as is usually observed in planar geometry. Less surprisingly, reshocks process the heavy–light mixing layer as in the planar case. In both configurations, the incident imploding shock and the reshocks induce Richtmyer–Meshkov (RM) instabilities at the density layer. However, we observe differences in the mixing-layer growth because the RM instability occurrences, Rayleigh–Taylor (RT) unstable scenarios (due to the radially accelerated motion of the layer) and phase inversion events are different. A small-amplitude stability analysis along the lines of Bell (Los Alamos Scientific Laboratory Report, LA-1321, 1951) and Plesset (J. Appl. Phys., vol. 25, 1954, pp. 96–98) helps quantify the effects of the mean flow on the mixing-layer growth by decoupling the effects of RT/RM instabilities from Bell–Plesset effects associated with geometric convergence and compressibility for arbitrary convergence ratios. The analysis indicates that baroclinic instabilities are the dominant effect, considering the low convergence ratio (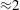${\approx } 2$) and rather high (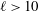$\ell >10$) mode numbers considered.

JFM classification

Turbulent Flows: Compressible turbulence Compressible Flows: Shock waves Mixing: Turbulent mixing
Type
Papers
Information
Journal of Fluid Mechanics , Volume 748 , 10 June 2014 , pp. 85 - 112
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Balakrishnan, K. & Menon, S. 2011 Characterization of the mixing layer resulting from the detonation of heterogeneous explosive charges. Flow Turbul. Combust. 87, 639–671.Google Scholar
Barnes, C. W., Batha, S. H., Dunne, A. M., Magelssen, G. R., Rothman, S., Day, R. D., Elliott, N. E., Haynes, D. A., Holmes, R. L., Scott, J. M., Tubbs, D. L., Youngs, D. L., Boehly, T. R. & Jaanimagi, P. 2002 Observation of mix in a compressible plasma in a convergent cylindrical geometry. Phys. Plasmas 9 (11), 4431–4434.CrossRefGoogle Scholar
Bell, G. I.1951 Taylor instability on cylinders and spheres in small amplitude approximation. Los Alamos Scientific Laboratory Report, LA-1321.Google Scholar
Berger, M. J. & Colella, P. 1989 Local adaptive mesh refinement for shock hydrodynamics. J. Comput. Phys. 82 (1), 64–84.CrossRefGoogle Scholar
Chisnell, R. F. 1998 An analytic description of converging shock waves. J. Fluid Mech. 354, 357–375.CrossRefGoogle Scholar
Cook, A. W., Cabot, W. & Miller, P. L. 2004 The mixing transition in Rayleigh–Taylor instability. J. Fluid Mech. 511, 333–362.Google Scholar
Deiterding, R. 2005 Construction and application of an AMR algorithm for distributed memory computers. In Adaptive Mesh Refinement – Theory and Applications (ed. Plewa, T., Linde, T. & Weirs, V. G.), Lecture Notes in Computational Science and Engineering, vol. 41, pp. 361–372. Springer.Google Scholar
Fedkiw, R. P., Aslam, T., Merriman, B. & Osher, S. 1999 A non-oscillatory Eulerian approach to interfaces in multimaterial flows (the ghost fluid method). J. Comput. Phys. 152 (2), 457–492.CrossRefGoogle Scholar
Friedman, M. P. 1960 An improved perturbation theory for shock waves propagating through non-uniform regions. J. Fluid Mech. 8, 193–209.CrossRefGoogle Scholar
Gittings, M., Weaver, R., Clover, M., Betlach, T., Byrne, N., Coker, R., Dendy, E., Hueckstaedt, R., New, K., Oakes, W. R., Ranta, D. & Stefan, R. 2008 The RAGE radiation-hydrodynamic code. Comput. Sci. Disc. 1 (1), 015005.CrossRefGoogle Scholar
Glimm, J., Grove, J. W., Zhang, Y. & Dutta, S. 2002 Numerical study of axisymmetric Richtmyer–Meshkov instability and azimuthal effect on spherical mixing. J. Stat. Phys. 107 (1/2), 241–260.Google Scholar
Gottlieb, S., Shu, C. -W. & Tadmor, E. 2001 Strong stability-preserving high-order time discretization methods. SIAM Rev. 43 (1), 89–112.CrossRefGoogle Scholar
Guderley, G. 1942 Starke Kugelige und zylindrische Verdichtungsstösse in der Nähe des Kugelmittelpunktes bzw der Zylinderachse. Luftfahrtforschung 19, 302–312.Google Scholar
Hill, D. J. & Pullin, D. I. 2004 Hybrid tuned centre-difference–WENO method for large eddy simulations in the presence of strong shocks. J. Comput. Phys. 194 (2), 435–450.Google Scholar
Honein, A. E. & Moin, P. 2004 Higher entropy conservation and numerical stability of compressible turbulence simulations. J. Comput. Phys. 201 (2), 531–545.Google Scholar
Hosseini, S. H. R. & Takayama, K. 2005 Experimental study of Richtmyer–Meshkov instability induced by cylindrical shock waves. Phys. Fluids 17 (8), 084101.Google Scholar
Joggerst, C. C., Almgren, A. & Woosley, S. E. 2010 Three-dimensional simulations of Rayleigh–Taylor mixing in core-collapse supernovae. Astrophys. J. 723, 353–363.Google Scholar
Jun, B., Jones, T. W. & Norma, M. L. 1996 Interaction of Rayleigh–Taylor fingers and circumstellar cloudlets in young supernova remnants. Astrophys. J. 468, 59–63.Google Scholar
Krechetnikov, R. 2009 Rayleigh–Taylor and Richtmyer–Meshkov instabilities of flat and curved interfaces. J. Fluid Mech. 625, 387–410.Google Scholar
Krechetnikov, R. & Homsy, G. M. 2009 Crown-forming instability phenomena in the drop splash problem. J. Colloid Interface Sci. 331, 555–559.CrossRefGoogle ScholarPubMed
Kumar, S., Hornung, H. G. & Sturtevant, B. 2003 Growth of shocked gaseous interfaces in a conical geometry. Phys. Fluids 15 (10), 3194–3208.Google Scholar
Li, C. K., Séguin, F. H., Frenje, J. A., Petrasso, R. D., Delettrez, J. A., McKenty, P. W., Sangster, T. C., Keck, R. L., Soures, J. M., Marshall, F. J., Meyerhofer, D. D., Goncharov, V. N., Knauer, J. P., Radha, P. B., Regan, S. P. & Seka, W. 2004 Effects of nonuniform illumination on implosion asymmetry in direct-drive inertial confinement fusion. Phys. Rev. Lett. 92, 205001.CrossRefGoogle ScholarPubMed
Lin, H., Storey, B. D. & Szeri, A. J. 2002 Rayleigh–Taylor instability of violently collapsing bubbles. Phys. Fluids 14 (8), 2925–2928.Google Scholar
Lindl, J. D. 1998 Inertial Confinement Fusion: The Quest for Ignition and Energy Gain using Indirect Drive. Springer.Google Scholar
Lombardini, M.2008 Richtmyer–Meshkov instability in converging geometries. PhD Thesis, California Institute of Technology. http://thesis.library.caltech.edu/2319/.Google Scholar
Lombardini, M. & Deiterding, R. 2010 Large-eddy simulations of Richtmyer–Meshkov instability in a converging geometry. Phys. Fluids 22 (9), 091112.Google Scholar
Lombardini, M., Hill, D. J., Pullin, D. I. & Meiron, D. I. 2011 Atwood ratio dependence of Richtmyer–Meshkov flows under reshock conditions using large-eddy simulations. J. Fluid Mech. 670, 439–480.Google Scholar
Lombardini, M. & Pullin, D. I. 2009 Small-amplitude perturbations in the three-dimensional cylindrical Richtmyer–Meshkov instability. Phys. Fluids 21 (11), 114103.Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2012 Transition to turbulence in shock-driven mixing: a Mach number study. J. Fluid Mech. 690, 203–226.Google Scholar
Lombardini, M., Pullin, D. I. & Meiron, D. I. 2014 Turbulent mixing driven by spherical implosions. Part 2. Turbulence statistics. J. Fluid Mech. 748, 113–142.Google Scholar
Mankbadi, M. R. & Balachandar, S. 2012 Compressible inviscid instability of rapidly expanding spherical material interfaces. Phys. Fluids 24 (3), 034106.Google Scholar
Meshkov, E. E. 1969 Instability of the interface of two gases accelerated by a shock wave. Sov. Fluid Dyn. 4 (5), 101–108.Google Scholar
Mikaelian, K. O. 1990 Rayleigh–Taylor and Richtmyer–Meshkov instabilities and mixing in stratified spherical shells. Phys. Rev. A 42, 3400–3420.CrossRefGoogle ScholarPubMed
Mikaelian, K. O. 2005 Rayleigh–Taylor and Richtmyer–Meshkov instabilities and mixing in stratified cylindrical shells. Phys. Fluids 17 (9), 094105.CrossRefGoogle Scholar
Misra, A. & Pullin, D. I. 1997 A vortex-based model for large-eddy simulation. Phys. Fluids 9 (8), 2443–2454.Google Scholar
Motl, B., Oakley, J., Ranjan, D., Weber, C., Anderson, M. & Bonazza, R. 2009 Experimental validation of a Richtmyer–Meshkov scaling law over large density ratio and shock strength ranges. Phys. Fluids 21 (12), 126102.CrossRefGoogle Scholar
Orlicz, G. C., Balakumar, B. J., Tomkins, C. D. & Prestridge, K. P. 2009 A Mach number study of the Richtmyer–Meshkov instability in a varicose, heavy-gas curtain. Phys. Fluids 21 (6), 064102.Google Scholar
Pantano, C., Deiterding, R., Hill, D. J. & Pullin, D. I. 2007 A low numerical dissipation patch-based adaptive mesh refinement method for large-eddy simulation of compressible flows. J. Comput. Phys. 221 (1), 63–87.CrossRefGoogle Scholar
Plesset, M. S. 1954 On the stability of fluid flows with spherical symmetry. J. Appl. Phys. 25, 96–98.CrossRefGoogle Scholar
Pullin, D. I. 2000 A vortex-based model for the subgrid flux of a passive scalar. Phys. Fluids 12 (9), 2311–2319.Google Scholar
Richtmyer, R. D. 1960 Taylor instability in shock acceleration of compressible fluids. Commun. Pure Appl. Maths 13, 297–319.Google Scholar
Taylor, G. I. 1950 The instability of liquid surfaces when accelerated in a direction perpendicular to their planes. Proc. R. Soc. Lond. A 201, 192–196.Google Scholar
Thomas, V. A. & Kares, R. J. 2012 Drive asymmetry and the origin of turbulence in an ICF implosion. Phys. Rev. Lett. 109 (7), 075004.Google Scholar
Thornber, D., Drikakis, D. L., Youngs, D. L. & Williams, R. J. R. 2010 The influence of initial conditions on turbulent mixing due to Richtmyer–Meshkov instability. J. Fluid Mech. 654, 99–139.Google Scholar
Vandenboomgaerde, M., Mügler, C. & Gauthier, S. 1998 Impulsive model for the Richtmyer–Meshkov instability. Phys. Rev. E 58 (2), 1874–1882.CrossRefGoogle Scholar
Vetter, M. & Sturtevant, B. 1995 Experiments on the Richtmyer–Meshkov instability of an air/ ${SF}_6$ interface. Shock Waves 4, 247–252.Google Scholar
Wecken, F. 1950 Expansion einer Gaskugel hohen Druckes. Z. Angew. Math. Mech. 30, 270–271.CrossRefGoogle Scholar
Welser-Sherrill, L., Haynes, D. A., Mancini, R. C., Cooley, J. H., Tommasini, R., Golovkin, I. E., Sherrill, M. E. & Haan, S. W. 2008 Inference of ICF implosion core mix using experimental data and theoretical mix modelling. High Energ. Dens. Phys. 5 (4), 249–257.Google Scholar
Youngs, D. L. & Williams, R. J. R. 2008 Turbulent mixing in spherical implosions. Intl J. Numer. Meth. Fluids 56 (8), 1597–1603.CrossRefGoogle Scholar
Yu, H. & Livescu, D. 2008 Rayleigh–Taylor instability in cylindrical geometry with compressible fluids. Phys. Fluids 20 (10), 104103.CrossRefGoogle Scholar
Zhang, Q. & Graham, M. J. 1998 A numerical study of Richtmyer–Meshkov instability driven by cylindrical shocks. Phys. Fluids 10 (4), 974–992.Google Scholar