Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Duraisamy, Karthik
2021.
Perspectives on machine learning-augmented Reynolds-averaged and large eddy simulation models of turbulence.
Physical Review Fluids,
Vol. 6,
Issue. 5,
Morimoto, Masaki
Fukami, Kai
and
Fukagata, Koji
2021.
Experimental velocity data estimation for imperfect particle images using machine learning.
Physics of Fluids,
Vol. 33,
Issue. 8,
Akolekar, Harshal D.
Waschkowski, Fabian
Zhao, Yaomin
Pacciani, Roberto
and
Sandberg, Richard D.
2021.
Transition Modeling for Low Pressure Turbines Using Computational Fluid Dynamics Driven Machine Learning.
Energies,
Vol. 14,
Issue. 15,
p.
4680.
Milani, Pedro M.
Ling, Julia
and
Eaton, John K.
2021.
On the generality of tensor basis neural networks for turbulent scalar flux modeling.
International Communications in Heat and Mass Transfer,
Vol. 128,
Issue. ,
p.
105626.
Xu, Xiaowei
Ooi, Andrew
and
Sandberg, Richard D.
2021.
Data-driven algebraic models of the turbulent Prandtl number for buoyancy-affected flow near a vertical surface.
International Journal of Heat and Mass Transfer,
Vol. 179,
Issue. ,
p.
121737.
Srivastava, Vishal
and
Duraisamy, Karthik
2021.
Generalizable physics-constrained modeling using learning and inference assisted by feature-space engineering.
Physical Review Fluids,
Vol. 6,
Issue. 12,
Waschkowski, Fabian
Zhao, Yaomin
Sandberg, Richard
and
Klewicki, Joseph
2022.
Multi-objective CFD-driven development of coupled turbulence closure models.
Journal of Computational Physics,
Vol. 452,
Issue. ,
p.
110922.
Morimoto, Masaki
Fukami, Kai
Zhang, Kai
and
Fukagata, Koji
2022.
Generalization techniques of neural networks for fluid flow estimation.
Neural Computing and Applications,
Vol. 34,
Issue. 5,
p.
3647.
Sikirica, Ante
Grbčić, Luka
Alvir, Marta
and
Kranjčević, Lado
2022.
Computational Efficiency Assessment of Adaptive Mesh Refinement for Turbulent Jets in Crossflow.
Mathematics,
Vol. 10,
Issue. 4,
p.
620.
Berrone, S.
and
Oberto, D.
2022.
An invariances-preserving vector basis neural network for the closure of Reynolds-averaged Navier–Stokes equations by the divergence of the Reynolds stress tensor.
Physics of Fluids,
Vol. 34,
Issue. 9,
Wang, Yaning
Wang, Zirui
Wang, Wen
Li, Honglin
Shen, Weiqi
and
Cui, Jiahuan
2022.
Predicting and optimizing multirow film cooling with trenches using gated recurrent unit neural network.
Physics of Fluids,
Vol. 34,
Issue. 4,
Steiner, Julia
Dwight, Richard P.
and
Viré, Axelle
2022.
Data-driven RANS closures for wind turbine wakes under neutral conditions.
Computers & Fluids,
Vol. 233,
Issue. ,
p.
105213.
Xing, Haifeng
Luo, Lei
Du, Wei
and
Wang, Songtao
2022.
Direct and Inverse Model for Single-Hole Film Cooling With Machine Learning.
Journal of Turbomachinery,
Vol. 144,
Issue. 4,
Strijhak, Sergei
Ryazanov, Daniil
Koshelev, Konstantin
and
Ivanov, Aleksandr
2022.
Neural Network Prediction for Ice Shapes on Airfoils Using iceFoam Simulations.
Aerospace,
Vol. 9,
Issue. 2,
p.
96.
Xu, Xiaowei
Waschkowski, Fabian
Ooi, Andrew S.H.
and
Sandberg, Richard D.
2022.
Towards robust and accurate Reynolds-averaged closures for natural convection via multi-objective CFD-driven machine learning.
International Journal of Heat and Mass Transfer,
Vol. 187,
Issue. ,
p.
122557.
Sandberg, Richard D.
and
Zhao, Yaomin
2022.
Machine-learning for turbulence and heat-flux model development: A review of challenges associated with distinct physical phenomena and progress to date.
International Journal of Heat and Fluid Flow,
Vol. 95,
Issue. ,
p.
108983.
Williams, J.
Wolfram, U.
and
Ozel, A.
2022.
Neural stochastic differential equations for particle dispersion in large-eddy simulations of homogeneous isotropic turbulence.
Physics of Fluids,
Vol. 34,
Issue. 11,
Parish, Eric
Ching, David S.
Miller, Nathan E.
Beresh, Steven J.
and
Barone, Matthew F.
2023.
Turbulence modeling for compressible flows using discrepancy tensor-basis neural networks and extrapolation detection.
Röhrs, Johannes
Halsne, Trygve
Sutherland, Graig
Dagestad, Knut-Frode
Hole, Lars Robert
Broström, Göran
and
Christensen, Kai H.
2023.
Current shear and turbulence during a near-inertial wave.
Frontiers in Marine Science,
Vol. 10,
Issue. ,
Shankar, Varun
Puri, Vedant
Balakrishnan, Ramesh
Maulik, Romit
and
Viswanathan, Venkatasubramanian
2023.
Differentiable physics-enabled closure modeling for Burgers’ turbulence.
Machine Learning: Science and Technology,
Vol. 4,
Issue. 1,
p.
015017.
 $r=1$ and
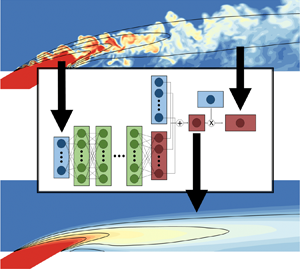
$r=1$ and  $r=2$, using highly resolved large eddy simulations. First, an investigation of turbulent scalar mixing sheds light onto the previously observed but unexplained phenomenon of negative turbulent diffusivity. We identify two distinct types of counter gradient transport, prevalent in different regions: the first, throughout the windward shear layer, is caused by cross-gradient transport; the second, close to the wall right after injection, is caused by non-local effects. Then, we propose a deep learning approach for modelling the turbulent scalar flux by adapting the tensor basis neural network previously developed to model Reynolds stresses (Ling et al., J. Fluid Mech., vol. 807, 2016a, pp. 155–166). This approach uses a deep neural network with embedded coordinate frame invariance to predict a tensorial turbulent diffusivity that is not explicitly available in the high-fidelity data used for training. After ensuring analytically that the matrix diffusivity leads to a stable solution for the advection diffusion equation, we apply this approach in the inclined jets in crossflow under study. The results show significant improvement compared to a simple model, particularly where cross-gradient effects play an important role in turbulent mixing. The model proposed herein is not limited to jets in crossflow; it can be used in any turbulent flow where the Reynolds averaged transport of a scalar is considered.
$r=2$, using highly resolved large eddy simulations. First, an investigation of turbulent scalar mixing sheds light onto the previously observed but unexplained phenomenon of negative turbulent diffusivity. We identify two distinct types of counter gradient transport, prevalent in different regions: the first, throughout the windward shear layer, is caused by cross-gradient transport; the second, close to the wall right after injection, is caused by non-local effects. Then, we propose a deep learning approach for modelling the turbulent scalar flux by adapting the tensor basis neural network previously developed to model Reynolds stresses (Ling et al., J. Fluid Mech., vol. 807, 2016a, pp. 155–166). This approach uses a deep neural network with embedded coordinate frame invariance to predict a tensorial turbulent diffusivity that is not explicitly available in the high-fidelity data used for training. After ensuring analytically that the matrix diffusivity leads to a stable solution for the advection diffusion equation, we apply this approach in the inclined jets in crossflow under study. The results show significant improvement compared to a simple model, particularly where cross-gradient effects play an important role in turbulent mixing. The model proposed herein is not limited to jets in crossflow; it can be used in any turbulent flow where the Reynolds averaged transport of a scalar is considered.

