Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Chapman, Piers
Socolofsky, Scott
and
Hetland, Robert
2014.
FROM BLOWOUT TO BEACH: AN INTEGRATED MODELING APPROACH.
International Oil Spill Conference Proceedings,
Vol. 2014,
Issue. 1,
p.
919.
Wallace, James M.
2016.
Quadrant Analysis in Turbulence Research: History and Evolution.
Annual Review of Fluid Mechanics,
Vol. 48,
Issue. 1,
p.
131.
Lacassagne, Tom
El-Hajem, Mahmoud
Morge, Fabien
Simoens, Serge
Champagne, Jean-Yves
and
Augier, F.
2017.
Study of Gas Liquid Mass Transfer in a Grid Stirred Tank.
Oil & Gas Science and Technology – Revue d’IFP Energies nouvelles,
Vol. 72,
Issue. 1,
p.
7.
Szeri, Andrew J.
2017.
Boundary layers at a dynamic interface: Air‐sea exchange of heat and mass.
Journal of Geophysical Research: Oceans,
Vol. 122,
Issue. 4,
p.
2781.
de Lamotte, Anne
Delafosse, Angélique
Calvo, Sébastien
Delvigne, Frank
and
Toye, Dominique
2017.
Investigating the effects of hydrodynamics and mixing on mass transfer through the free-surface in stirred tank bioreactors.
Chemical Engineering Science,
Vol. 172,
Issue. ,
p.
125.
Flores, Oscar
Riley, James J.
and
Horner-Devine, Alexander R.
2017.
On the dynamics of turbulence near a free surface.
Journal of Fluid Mechanics,
Vol. 821,
Issue. ,
p.
248.
Katul, Gabriel
Peltola, Olli
Grönholm, Tiia
Launiainen, Samuli
Mammarella, Ivan
and
Vesala, Timo
2018.
Ejective and Sweeping Motions Above a Peatland and Their Role in Relaxed-Eddy-Accumulation Measurements and Turbulent Transport Modelling.
Boundary-Layer Meteorology,
Vol. 169,
Issue. 2,
p.
163.
Johnson, Blair A.
and
Cowen, Edwin A.
2018.
Turbulent boundary layers absent mean shear.
Journal of Fluid Mechanics,
Vol. 835,
Issue. ,
p.
217.
Lacassagne, Tom
Simoëns, Serge
El Hajem, Mahmoud
and
Champagne, Jean-Yves
2018.
Ratiometric, single-dye, pH-sensitive inhibited laser-induced fluorescence for the characterization of mixing and mass transfer.
Experiments in Fluids,
Vol. 59,
Issue. 1,
Lacassagne, T.
Simoëns, S.
EL Hajem, M.
Lyon, A.
and
Champagne, J.-Y.
2019.
Oscillating grid turbulence in shear-thinning polymer solutions.
Physics of Fluids,
Vol. 31,
Issue. 8,
Herlina, H.
and
Wissink, J. G.
2019.
Simulation of air–water interfacial mass transfer driven by high-intensity isotropic turbulence.
Journal of Fluid Mechanics,
Vol. 860,
Issue. ,
p.
419.
Lacassagne, T.
Simoëns, S.
EL Hajem, M.
and
Champagne, J.-Y.
2020.
Oscillating grid generating turbulence near gas-liquid interfaces in shear-thinning dilute polymer solutions.
Physical Review Fluids,
Vol. 5,
Issue. 3,
Sanjou, M.
2020.
Local gas transfer rate through the free surface in spatially accelerated open-channel turbulence.
Physics of Fluids,
Vol. 32,
Issue. 10,
Heisel, Michael
Katul, Gabriel G.
Chamecki, Marcelo
and
Guala, Michele
2020.
Velocity asymmetry and turbulent transport closure in smooth- and rough-wall boundary layers.
Physical Review Fluids,
Vol. 5,
Issue. 10,
Petrolo, Diana
and
Longo, Sandro
2020.
Buoyancy transfer in a two-layer system in steady state. Experiments in a Taylor–Couette cell.
Journal of Fluid Mechanics,
Vol. 896,
Issue. ,
Lacassagne, Tom
Simoëns, Serge
EL Hajem, Mahmoud
and
Champagne, Jean‐Yves
2021.
POD analysis of oscillating grid turbulence in water and shear thinning polymer solution.
AIChE Journal,
Vol. 67,
Issue. 1,
Xuan, Anqing
and
Shen, Lian
2022.
Analyses of wave-phase variation of Reynolds shear stress underneath surface wave using streamline coordinates.
Journal of Fluid Mechanics,
Vol. 931,
Issue. ,
Erinin, M. A.
Néel, B.
Ruth, D. J.
Mazzatenta, M.
Jaquette, R. D.
Veron, F.
and
Deike, L.
2022.
Speed and Acceleration of Droplets Generated by Breaking Wind‐Forced Waves.
Geophysical Research Letters,
Vol. 49,
Issue. 13,
Lacassagne, Tom
EL Hajem, Mahmoud
Champagne, Jean-Yves
and
Simoëns, Serge
2022.
Turbulent mass transfer near gas-liquid interfaces in water and shear-thinning dilute polymer solution.
International Journal of Heat and Mass Transfer,
Vol. 194,
Issue. ,
p.
122975.
Lacassagne, Tom
EL Hajem, Mahmoud
Champagne, Jean-Yves
and
Simoëns, Serge
2023.
Systematic error and correction of intensity-based I-PLIF for local pH and concentration measurements in unsteady boundary layers.
Experiments in Fluids,
Vol. 64,
Issue. 11,
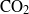 ${\mathrm{CO} }_{2} $ gas above a water tank that has been initially purged of dissolved
${\mathrm{CO} }_{2} $ gas above a water tank that has been initially purged of dissolved 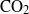 ${\mathrm{CO} }_{2} $ . We measure velocity and concentration fluctuations below the air–water interface, from the viscous sublayer to the middle of the ‘source region’ where the effects of the surface are first felt. Our laboratory measurement technique uses quantitative imaging to collect simultaneous concentration and velocity fields, which are measured at a resolution that reveals the dynamics in the turbulent inertial subrange. Two-point statistics reveal the spatial structure of velocity and concentration fluctuations, and are examined as a function of depth beneath the air–water interface. There is a clear dominance of large scales at all depths for all quantities, but the relative importance of scales changes markedly with proximity to the interface. Quadrant analysis of the turbulent scalar flux shows a four-way balance of flux components far from the interface, which near the interface evolves into a two-way balance between motions that are raising and lowering parcels of low-concentration fluid.
${\mathrm{CO} }_{2} $ . We measure velocity and concentration fluctuations below the air–water interface, from the viscous sublayer to the middle of the ‘source region’ where the effects of the surface are first felt. Our laboratory measurement technique uses quantitative imaging to collect simultaneous concentration and velocity fields, which are measured at a resolution that reveals the dynamics in the turbulent inertial subrange. Two-point statistics reveal the spatial structure of velocity and concentration fluctuations, and are examined as a function of depth beneath the air–water interface. There is a clear dominance of large scales at all depths for all quantities, but the relative importance of scales changes markedly with proximity to the interface. Quadrant analysis of the turbulent scalar flux shows a four-way balance of flux components far from the interface, which near the interface evolves into a two-way balance between motions that are raising and lowering parcels of low-concentration fluid.
