Hostname: page-component-78c5997874-t5tsf Total loading time: 0 Render date: 2024-11-10T06:48:47.115Z Has data issue: false hasContentIssue false
  • English
  • Français

Two- and three-dimensional wake transitions of an impulsively started uniformly rolling circular cylinder

Published online by Cambridge University Press:  02 August 2017

F. Y. Houdroge Open the ORCID record for F. Y. Houdroge [Opens in a new window] ,
T. Leweke ,
K. Hourigan  and
M. C. Thompson
F. Y. Houdroge*
Affiliation:
FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC, 3800, Australia
T. Leweke
Affiliation:
IRPHE, CNRS, Aix-Marseille Université, Centrale Marseille, 13384 Marseille, France
K. Hourigan
Affiliation:
FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC, 3800, Australia
M. C. Thompson
Affiliation:
FLAIR, Department of Mechanical and Aerospace Engineering, Monash University, Clayton, VIC, 3800, Australia
*
†Email address for correspondence: farah.houdroge@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

This paper presents the characteristics of the different stages in the evolution of the wake of a circular cylinder rolling without slipping along a wall at constant speed, acquired through numerical stability analysis and two- and three-dimensional numerical simulations. Reynolds numbers between 30 and 300 are considered. Of importance in this study is the transition to three-dimensionality from the underlying two-dimensional periodic flow and, in particular, the way that the associated transitions influence the fluid forces exerted on the cylinder and the development and the structure of the wake. It is found that the steady two-dimensional flow becomes unstable to three-dimensional perturbations at 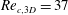$Re_{c,3D}=37$, and that the transition to unsteady two-dimensional flow – or periodic vortex shedding – occurs at 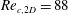$Re_{c,2D}=88$, thus validating and refining the results of Stewart et al. (J. Fluid Mech. vol. 648, 2010, pp. 225–256). The main focus here is on Reynolds numbers beyond the transition to unsteady flow at 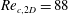$Re_{c,2D}=88$. From impulsive start up, the wake almost immediately undergoes transition to a periodic two-dimensional wake state, which, in turn, is three-dimensionally unstable. Thus, the previous three-dimensional stability analysis based on the two-dimensional steady flow provides only an element of the full story. Floquet analysis based on the periodic two-dimensional flow was undertaken and new three-dimensional instability modes were revealed. The results suggest that an impulsively started cylinder rolling along a surface at constant velocity for 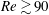$Re\gtrsim 90$ will result in the rapid development of a periodic two-dimensional wake that will be maintained for a considerable time prior to the wake undergoing three-dimensional transition. Of interest, the mean lift and drag coefficients obtained from full three-dimensional simulations match predictions from two-dimensional simulations to within a few per cent.

JFM classification

Aerodynamics: Aerodynamics Wakes/Jets: Wakes
Type
Papers
Information
Journal of Fluid Mechanics , Volume 826 , 10 September 2017 , pp. 32 - 59
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akoury, R. E., Braza, M., Perrin, R., Harran, G. & Hoarau, Y. 2008 The three-dimensional transition in the flow around a rotating cylinder. J. Fluid Mech. 607, 1–11.Google Scholar
Armaly, B. F., Durst, F., Pereira, J. C. F. & Schönung, B. 1983 Experimental and theoretical investigation of backward-facing step flow. J. Fluid Mech. 127, 473–496.Google Scholar
Arnal, M. P., Goering, D. J. & Humphrey, J. A. C. 1991 Vortex shedding from a bluff body adjacent to a plane sliding wall. Trans. ASME J. Fluids Engng 113, 384–398.CrossRefGoogle Scholar
Barkley, D. 2006 Linear analysis of the cylinder wake mean flow. Europhys. Lett. 75, 750–756.Google Scholar
Barkley, D., Gomes, M. G. M. & Henderson, R. D. 2002 Three-dimensional instability in flow over a backward-facing step. J. Fluid Mech. 473, 167–190.Google Scholar
Barkley, D. & Henderson, R. D. 1996 Three-dimensional Floquet stability analysis of the wake of a circular cylinder. J. Fluid Mech. 322, 215–241.Google Scholar
Bayly, B. J. 1986 Three-dimensional instability of elliptical flow. Phys. Rev. Lett. 57, 2160–2163.Google Scholar
Bénard, H. 1908 Formation de centres de giration à l’arrière d’un obstacle en mouvement. C. R. Acad. Sci. Paris 147, 839–970.Google Scholar
Chorin, A. J. 1968 Numerical solution of the Navier–Stokes equations. Maths Comput. 22, 745–762.Google Scholar
Crouch, J. 2005 Airplane trailing vortices and their control. C. R. Physique 6, 487–499.Google Scholar
Dennis, S. C. R. & Chang, G.-Z. 1970 Numerical solutions for steady flow past a circular cylinder at Reynolds numbers up to 100. J. Fluid Mech. 42, 471–489.Google Scholar
Díaz, F., Gavaldà, J., Kawall, J. G., Keffer, J. F. & Giralt, F. 1983 Vortex shedding from a spinning cylinder. Phys. Fluids 26, 3454–3460.Google Scholar
Elston, J. R., Sheridan, J. & Blackburn, H. M. 2004 Two-dimensional Floquet stability analysis of the flow produced by an oscillating circular cylinder in quiescent fluid. Eur. J. Mech. (B/Fluids) 23, 99–106.Google Scholar
Griffith, M. D., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2011 Vortex shedding and three-dimensional behaviour of flow past a cylinder confined in a channel. J. Fluids Struct. 27, 855–860.Google Scholar
Griffith, M. D., Thompson, M. C., Leweke, T., Hourigan, K. & Anderson, W. P. 2007 Wake behaviour and instability of flow through a partially blocked channel. J. Fluid Mech. 582, 319–340.Google Scholar
Henderson, R. D. 1997 Nonlinear dynamics and pattern formation in turbulent wake transition. J. Fluid Mech. 352, 65–112.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Proceedings of the 1988 Summer Program, pp. 193–208. Center for Turbulence Research.Google Scholar
Jacquin, J., Fabre, D., Sipp, D. & Coustols, E. 2005 Unsteadiness, instability and turbulence in trailing vortices. C. R. Physique 6, 399–414.Google Scholar
Jaminet, J. F. & Atta, C. C. W. Van 1969 Experiments on vortex shedding from rotating circular cylinders. AIAA J. 7, 1817–1819.Google Scholar
Jones, M. C., Hourigan, K. & Thompson, M. C. 2015 A study of the geometry and parameter dependence of vortex breakdown. Phys. Fluids 27, 044102.Google Scholar
von Kármán, T. 1911 Über den Mechanismus des Widerstandes, den ein bewegter Körper in einer Flüssigkeit erfährt. Nachr. Ges. Wiss. Göttingen, Math.-Phys. Kl. 1911, 509–517.Google Scholar
Karniadakis, G. E., Israeli, M. & Orszag, S. A. 1991 High-order splitting methods for the incompressible Navier–Stokes equations. J. Comput. Phys. 97, 414–443.Google Scholar
Karniadakis, G. E. & Sherwin, S. J. 1999 Spectral/HP Element Methods for CFD, 1st edn. Oxford University Press.Google Scholar
Karniadakis, G. E. & Triantafyllou, G. S. 1992 Three-dimensional dynamics and transition to turbulence in the wake of bluff objects. J. Fluid Mech. 238, 1–30.Google Scholar
Kerswell, R. R. 2002 Elliptical instability. Annu. Rev. Fluid Mech. 34, 83–113.CrossRefGoogle Scholar
Kumar, S., Cantu, C. & Gonzalez, B. 2011 Flow past a rotating cylinder at low and high rotation rates. Trans. ASME J. Fluids Engng 133, 041201.Google Scholar
Landman, M. J. & Saffman, P. G. 1987 The three-dimensional instability of strained vortices in a viscous fluid. Phys. Fluids 30, 2339–2342.Google Scholar
Le Dizès, S. & Laporte, F. 2002 Theoretical predictions for the elliptic instability in a two-vortex flow. J. Fluid Mech. 471, 169–201.Google Scholar
Le Dizès, S. & Verga, A. 2002 Viscous interaction of two co-rotating vortices before merging. J. Fluid Mech. 467, 389–410.Google Scholar
Le Gal, P. & Croquette, V. 2000 Visualization of the space-time impulse response of the subcritical wake of a cylinder. Phys. Rev. E 62, 4424–4426.Google Scholar
Lei, C., Cheng, L. & Kavanagh, K. 1999 Re-examination of the effect of a plane boundary on force and vortex shedding of a circular cylinder. J. Wind Engng Ind. Aerodyn. 80, 263–286.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2007 Three-dimensional transition in the wake of a transversely oscillating cylinder. J. Fluid Mech. 577, 79–104.Google Scholar
Leontini, J. S., Thompson, M. C. & Hourigan, K. 2010 A numerical study of global frequency selection in the time-mean wake of a circular cylinder. J. Fluid Mech. 645, 435–446.Google Scholar
Leweke, T., Dizès, S. L. & Williamson, C. H. K. 2016 Dynamics and instabilities of vortex pairs. Annu. Rev. Fluid Mech. 48, 507–541.Google Scholar
Leweke, T. & Williamson, C. H. K. 1997 Cooperative elliptic instability of a vortex pair. J. Fluid Mech. 360, 85.Google Scholar
Leweke, T. & Williamson, C. H. K. 1998 Three-dimensional instabilities in wake transition. Eur. J. Mech. (B/Fluids) 17, 571–586.Google Scholar
Mamun, C. K. & Tuckerman, L. S. 1995 Asymmetry and Hopf-bifurcation in spherical Couette flow. Phys. Fluids 7 (1), 80–91.Google Scholar
Meena, J., Sidharth, G. S., Khan, M. H. & Mittal, S. 2011 Three dimensional instabilities in flow past a spinning and translating cylinder. In IUTAM Symposium on Bluff Body Flows (ed. Mittal, S. & Biswas, G.), pp. 59–62. Indian Institute of Technology Kanpur.Google Scholar
Mittal, S. 2000 Flow past rotating cylinders: effect of eccentricity. Trans. ASME J. Appl. Mech. 68, 543–552.Google Scholar
Mittal, S. & Kumar, B. 2003 Flow past a rotating cylinder. J. Fluid Mech. 476, 303–334.Google Scholar
Pier, B. 2002 On the frequency selection of finite-amplitude vortex shedding in the cylinder wake. J. Fluid Mech. 458, 407–417.Google Scholar
Pierrehumbert, R. t. 1986 Universal short-wavelength instability of two-dimensional eddies in an inviscid fluid. Phys. Rev. Lett. 57, 2157.Google Scholar
Provansal, M., Mathis, C. & Boyer, L. 1987 Bénard-von Kármán instability: transient and forced regimes. J. Fluid Mech. 182, 1–22.Google Scholar
Radi, A., Thompson, M. C., Rao, A., Hourigan, K. & Sheridan, J. 2013 Experimental evidence of new three-dimensional modes in the wake of a rotating cylinder. J. Fluid Mech. 734, 567–594.Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013a Three-dimensionality in the wake of a rotating cylinder in a uniform flow. J. Fluid Mech. 717, 1–29.Google Scholar
Rao, A., Leontini, J. S., Thompson, M. C. & Hourigan, K. 2013b Three-dimensionality in the wake of a rapidly rotating cylinder in uniform flow. J. Fluid Mech. 730, 379–391.Google Scholar
Rao, A., Passaggia, P. Y., Bolnot, H., Thompson, M. C., Leweke, T. & Hourigan, K. 2012 Transition to chaos in the wake of a rolling sphere. J. Fluid Mech. 695, 135–148.Google Scholar
Rao, A., Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2011 Flows past rotating cylinders next to a wall. J. Fluids Struct. 27, 668–679.Google Scholar
Roshko, A.1954 On the development of turbulent wakes from vortex streets. NACA Tech. Rep. 1191 (formerly TN-2913).Google Scholar
Ryan, K., Thompson, M. C. & Hourigan, K. 2005 Three-dimensional transition in the wake of bluff elongated cylinders. J. Fluid Mech. 538, 1–29.Google Scholar
Sipp, D. & Lebedev, A. 2007 Global stability of base and mean flows: a general approach and its applications to cylinder and open cavity flows. J. Fluid Mech. 593, 333–358.Google Scholar
So, J., Ryan, K. & Sheard, G. J. 2011 Short-wave instabilities on a vortex pair of unequal strength circulation ratio. Appl. Math. Model. 35, 1581–1590.Google Scholar
Stewart, B. E.2008 The dynamics and stability of flows around rolling bluff bodies. PhD thesis, Monash University, Melbourne, Aunstralia and Université de Provence, Marseille, France.Google Scholar
Stewart, B. E., Hourigan, K., Thompson, M. C. & Leweke, T. 2006 Flow dynamics and forces associated with a cylinder rolling along a wall. Phys. Fluids 18, 111701.Google Scholar
Stewart, B. E., Thompson, M. C., Leweke, T. & Hourigan, K. 2010 The wake behind a cylinder rolling on a wall at varying rotation rates. J. Fluid Mech. 648, 225–256.Google Scholar
Taneda, S. 1956 Experimental investigation of the wakes behind cylinders and plates at low Reynolds numbers. J. Phys. Soc. Japan 11, 302–307.Google Scholar
Taneda, S. 1965 Experimental investigation of vortex streets. J. Phys. Soc. Japan 20, 1714–1721.CrossRefGoogle Scholar
Taneda, S. 1979 Visualization of separating Stokes flows. J. Phys. Soc. Japan 46, 1935–1942.Google Scholar
Tang, T. & Ingham, D. B. 1991 On steady flow past a rotating circular cylinder at Reynolds numbers 60 and 100. Comput. Fluids 19, 217–230.Google Scholar
Thompson, M. C. & Hourigan, K. 2003 The sensitivity of steady vortex breakdown bubbles in confined cylinder flows to rotating lid misalignment. J. Fluid Mech. 496, 129–138.Google Scholar
Thompson, M. C., Hourigan, K., Cheung, A. & Leweke, T. 2006 Hydrodynamics of a particle impact on a wall. Appl. Math. Model. 30, 1356–1369.Google Scholar
Thompson, M. C., Hourigan, K. & Sheridan, J. 1996 Three-dimensional instabilities in the wake of a circular cylinder. Exp. Therm. Fluid Sci. 12, 190–196.Google Scholar
Thompson, M. C. & Le Gal, P. 2004 The Stuart–Landau model applied to wake transition revisited. Eur. J. Mech. (B/Fluids) 23 (1), 219–228.Google Scholar
Thompson, M. C., Leweke, T. & Provansal, M. 2001a Kinematics and dynamics of sphere wake transition. J. Fluids Struct. 15, 575–586.Google Scholar
Thompson, M. C., Leweke, T. & Williamson, C. H. K. 2001b The physical mechanism of transition in bluff body wakes. J. Fluids Struct. 15, 607–616.Google Scholar
Turing, A. M. 1948 Rounding-off errors in matrix processes. Q. J. Mech. Appl. Maths 1, 287.Google Scholar
Waleffe, F. 1990 On the three-dimensional instability of strained vortices. Phys. Fluids A 2, 76.Google Scholar
Williamson, C. H. K. 1996a Three-dimensional wake transition. J. Fluid Mech. 328, 345–407.Google Scholar
Williamson, C. H. K. 1996b Vortex dynamics in the cylinder wake. Annu. Rev. Fluid Mech. 28, 477–539.Google Scholar
Williamson, C. H. K. 1988 The existence of two stages in the transition to three-dimensionality of a cylinder wake. Phys. Fluids 31, 3165–3168.Google Scholar
Winckelmans, G., Cocle, R., Dufresne, L. & Capart, R. 2005 Vortex methods and their application to trailing wake vortex simulations. C. R. Physique 6, 467–486.Google Scholar
Wu, J., Sheridan, J., Welsh, M. C. & Hourigan, K. 1996 Three-dimensional vortex structures in a cylinder wake. J. Fluid Mech. 312, 201–222.Google Scholar
Zienkiewicz, O. C. 1977 The Finite Element Method, 3rd edn. McGraw-Hill.Google Scholar