Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-25T19:41:17.208Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional hydrodynamics of a Janus particle vesicle

Published online by Cambridge University Press:  04 May 2022

Szu-Pei Fu Open the ORCID record for Szu-Pei Fu [Opens in a new window] ,
Bryan Quaife Open the ORCID record for Bryan Quaife [Opens in a new window] ,
Rolf Ryham Open the ORCID record for Rolf Ryham [Opens in a new window]  and
Y.-N. Young Open the ORCID record for Y.-N. Young [Opens in a new window]
Szu-Pei Fu*
Affiliation:
Department of Mathematics, Fordham University, Bronx, NY 10458, USA
Bryan Quaife
Affiliation:
Department of Scientific Computing, Florida State University, Tallahassee, FL 32306, USA
Rolf Ryham
Affiliation:
Department of Mathematics, Fordham University, Bronx, NY 10458, USA
Y.-N. Young
Affiliation:
Department of Mathematical Sciences, New Jersey Institute of Technology, Newark, NJ 07102, USA
*
†Email address for correspondence: sfu17@fordham.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

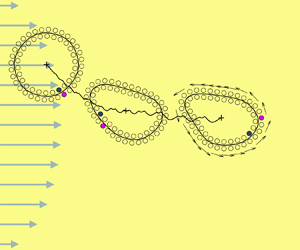
We develop a new model, to our knowledge, for the many-body hydrodynamics of amphiphilic Janus particles suspended in a viscous background flow. The Janus particles interact through a hydrophobic attraction potential that leads to self-assembly into bilayer structures. We adopt an efficient integral equation method for solving the screened Laplace equation for hydrophobic attraction and for solving the mobility problem for hydrodynamic interactions. The integral equation formulation accurately captures both interactions for near touched boundaries. Under a linear shear flow, we observe the tank-treading deformation in a two-dimensional vesicle made of Janus particles. The results yield measurements of intermonolayer friction, membrane permeability and, at large shear rates, membrane rupture. The simulation studies include a Janus particle vesicle in both linear and parabolic shear flows, and interactions between two Janus particle vesicles in shear and extensional flows. The hydrodynamics of the Janus particle vesicle is similar to the behaviour of an inextensible, elastic vesicle membrane with permeability.

JFM classification

Biological Fluid Dynamics: Collective behaviour Biological Fluid Dynamics: Membranes Low-Reynolds-number flows: Boundary integral methods
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 941 , 25 June 2022 , A41
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Abbasi, M., Farutin, A., Ez-Zahraouy, H., Benyoussef, A. & Misbah, C. 2021 Erythrocyte-erythrocyte aggregation dynamics under shear flow. Phys. Rev. Fluids 6, 023602.CrossRefGoogle Scholar
Balchunas, J., Cabanas, R.A., Zakhary, M.J., Gibaud, T., Fraden, S., Sharma, P., Hagan, M.F. & Dogic, Z. 2019 Equation of state of colloidal membranes. Soft Matt. 15, 6791–6802.CrossRefGoogle ScholarPubMed
Bao, Y., Rachh, M., Keaveny, E.E., Greengard, L. & Donev, A. 2018 A fluctuating boundary integral method for Brownian suspensions. J. Comput. Phys. 374, 1094–1119.CrossRefGoogle Scholar
Bradley, L.C., Chen, W.-H., Stebe, K.J. & Lee, D. 2017 Janus and patchy colloids at fluid interfaces. Curr. Opin. Colloid Interface Sci. 30, 25–33.CrossRefGoogle Scholar
Bradley, L.C., Stebe, K.J. & Lee, D. 2016 Clickable janus particles. J. Am. Chem. Soc. 138 (36), 11437–11440.CrossRefGoogle ScholarPubMed
Brandner, A.F., Timr, S., Melchionna, S., Derreumaux, P., Baaden, M. & Sterpone, F. 2019 Modelling lipid systems in fluid with Lattice Boltzmann Molecular Dynamics simulations and hydrodynamics. Sci. Rep. 9 (1), 16450.CrossRefGoogle Scholar
Bystricky, L., Shanbhag, S. & Quaife, B. 2020 Stable and contact-free time stepping for dense rigid particle suspensions. Intl J. Numer. Meth. Fluids 92 (2), 94–113.CrossRefGoogle Scholar
Cawthorn, C.J. & Balmforth, N.J. 2010 Contact in a viscous fluid. Part 1. A falling wedge. J. Fluid Mech. 646, 327–338.CrossRefGoogle Scholar
Chabanon, M., Ho, J.C.S., Liedberg, B., Parikh, A.N. & Rangamani, P. 2017 Pulsatile lipid vesicles under Osmotic Stress. Biophys. J. 112, 1682–1691.CrossRefGoogle ScholarPubMed
Corona, E., Greengard, L., Rachh, M. & Veerapaneni, S. 2017 An integral equation formulation for rigid bodies in Stokes flow in three dimensions. J. Comput. Phys. 332, 504–519.CrossRefGoogle Scholar
Corona, E. & Veerapaneni, S. 2018 Boundary integral equation analysis for suspension of spheres in Stokes flow. J. Comput. Phys. 362, 327–345.CrossRefGoogle Scholar
Coupier, G., Kaoui, B., Pokgorski, T. & Misbah, C. 2008 Noninertial lateral migration of vesicles in bounded poiseuille flow. Phys. Fluids 20, 111702.CrossRefGoogle Scholar
Danker, G., Vlahovska, P.M. & Misbah, C. 2009 Vesicles in Poiseuille Flow. Phys. Rev. Lett. 102, 148102.CrossRefGoogle ScholarPubMed
Feng, Z.-G. & Michaelides, E.E. 2004 The immersed boundary-lattice Boltzmann method for solving fluid–particles interaction problems. J. Comput. Phys. 195, 602–628.CrossRefGoogle Scholar
Finken, R., Lamura, A., Seifert, U. & Gompper, G. 2008 Two-dimensional fluctuating vesicles in linear shear flow. Eur. Phys. J. E 25 (3), 309–321.CrossRefGoogle ScholarPubMed
Fu, S.-P.P., Ryham, R., Klöckner, A., Wala, M., Jiang, S. & Young, Y.-N. 2020 Simulation of multiscale hydrophobic lipid dynamics via efficient integral equation methods. Multiscale Model. Simul. 18 (1), 79–103.CrossRefGoogle Scholar
de Gennes, P.-G. 1991 Soft matter. Nobel Lecture.CrossRefGoogle Scholar
Glowinski, R., Pan, T.W., Hesla, T.I., Joseph, D.D. & Périaux, J. 2001 A fictitious domain approach to the direct numerical simulation of incompressible viscous flow past moving rigid bodies: application to particulate flow. J. Comput. Phys. 169, 363–426.CrossRefGoogle Scholar
Jeffery, G.B. 1922 The motion of ellipsoidal particles immersed in a viscous fluid. Proc. R. Soc. A 102 (715), 161–179.Google Scholar
Kabacaoğlu, G., Quaife, B. & Biros, G. 2018 Low-resolution simulations of vesicle suspensions in 2D. J. Comput. Phys. 357, 43–77.CrossRefGoogle Scholar
Kaoui, B., Biros, G. & Misbah, C. 2009 Why do red blood cells have asymmetric shapes even in a symmetric flow? Phys. Rev. Lett. 103, 188101.CrossRefGoogle Scholar
Kaoui, B. & Harting, J. 2016 Two-dimensional Lattice Boltzmann simulations of vesicles with viscosity contrast. Rheol. Acta 55 (6), 465–475.CrossRefGoogle Scholar
Keller, S.R. & Skalak, R. 1982 Motion of a tank-treading ellipsoidal particle in a shear flow. J. Fluid Mech. 120, 27–47.CrossRefGoogle Scholar
Klöckner, A., Barnett, A., Greengard, L. & O'Neil, M. 2013 Quadrature by expansion: a new method for the evaluation of layer potentials. J. Comput. Phys. 252, 332–349.CrossRefGoogle Scholar
Lu, L., Rahimian, A. & Zorin, D. 2017 Contact-aware simulations of particulate Stokesian suspensions. J. Comput. Phys. 347, 160–182.CrossRefGoogle Scholar
Mallory, S.A., Alarcon, F., Cacciuto, A. & Valeriani, C. 2017 Self-assembly of active amphiphilic janus particles. New J. Phys. 19 (12), 125014.CrossRefGoogle Scholar
Nagle, J.F. & Tristram-Nagle, S. 2000 Structure of lipid bilayers. Biochim. Biophys. Acta 1469 (3), 159–195.CrossRefGoogle ScholarPubMed
Power, H. & Miranda, G. 1987 Second kind integral equation formulation of stokes’ flows past a particle of arbitrary shape. SIAM J. Appl. Maths 47 (4), 689–698.CrossRefGoogle Scholar
den Otter, W.K. & Shkulipa, S.A. 2007 Intermonolayer friction and surface shear viscosity of lipid bilayer membranes. Biophys. J. 93 (2), 423–433.CrossRefGoogle ScholarPubMed
Quaife, B. & Biros, G. 2014 High-volume fraction simulations of two-dimensional vesicle suspensions. J. Comput. Phys. 274, 245–267.CrossRefGoogle Scholar
Quaife, B., Gannon, A. & Young, Y.-N. 2021 Hydrodynamics of a semipermeable vesicle under flow and confinement. Phys. Rev. Fluids 6, 073601.CrossRefGoogle Scholar
Quaife, B., Veerapaneni, S. & Young, Y.-N. 2019 Hydrodynamics and rheology of a vesicle doublet suspension. Phys. Rev. Fluids 4, 103601.CrossRefGoogle Scholar
Rachh, M. & Greengard, L. 2016 Integral equation methods for elastance and mobility problems in two dimensions. SIAM J. Numer. Anal. 54 (5), 2889–2909.CrossRefGoogle Scholar
Schwalbe, J.T., Vlahovska, P.M. & Miksis, M.J. 2010 Monolayer slip effects on the dynamics of a lipid bilayer vesicle in a viscous flow. J. Fluid Mech. 647, 403–419.CrossRefGoogle Scholar
Veerapaneni, S.K., Young, Y.-N., Vlahovska, P.M. & Bławzdziewicz, J. 2011 Dynamics of a compound vesicle in shear flow. Phys. Rev. Lett. 106, 158103.CrossRefGoogle ScholarPubMed
Vlahovska, P.M. & Gracia, R.S. 2007 Dynamics of a viscous vesicle in linear flows. Phys. Rev. E 75, 016313.CrossRefGoogle ScholarPubMed
Vlahovska, P.M., Podgorski, T. & Misbah, C. 2009 Vesicles and red blood cells in flow: from individual dynamics to rheology, complex and biofluids. C. R. Phys. 10 (8), 775–789.CrossRefGoogle Scholar
Wohlert, J. & Edholm, O. 2006 Dynamics in atomistic simulations of phospholipid membranes: nuclear magnetic resonance relaxation rates and lateral diffusion. J. Chem. Phys. 125 (20), 204703.CrossRefGoogle ScholarPubMed
Yan, W., Corona, E., Malhotra, D., Veerapaneni, S. & Shelley, M. 2020 A scalable computational platform for particulate Stokes suspensions. J. Comput. Phys. 416, 109524.CrossRefGoogle Scholar
Zgorski, A., Pastor, R.W. & Lyman, E. 2019 Surface shear viscosity and interleaflet friction from nonequilibrium simulations of lipid bilayers. J. Chem. Theor. Comput. 15 (11), 6471–6481.CrossRefGoogle ScholarPubMed
Zhao, H. & Shaqfeh, E.S.G. 2011 The dynamics of a vesicle in simple shear flow. J. Fluid Mech. 674, 578–604.CrossRefGoogle Scholar

Fu et al. Supplementary Movie 1

There are 58 circular particles with radius 1.25 nm that form a self-enclosed bilayer structure. The simulation result shows the vesicle relaxation and the fluid pressure inside the JP vesicle decreases to 0 after a period of time. The color field from blue to red shows the magnitude of fluid pressure and the range from 0 to 0.1 pN nm-2. All dark blue dots in the domain are tracers that move with the calculated fluid motion. This movie includes the simulation results for 1 μs.

Download Fu et al. Supplementary Movie 1(Video)
Video 6.7 MB

Fu et al. Supplementary Movie 2

We adopt the relaxed configuration and place the JP vesicle in the shear flow. The simulation result shows a tank-treading motion for the shear rate χ=0.005. The colored field from dark blue to dark red shows the hydrophobic attraction activity and the range is from 0 to 1. All white dots in the domain are tracers in fluid that move with the fluid motion. This movie includes the simulation results for 4 μs.

Download Fu et al. Supplementary Movie 2(Video)
Video 12.6 MB

Fu et al. Supplementary Movie 3

Using the same setup demonstrated in Movie S2, we show the simulation result for inter-monolayer slip by tracking a pair of particles (blue and yellow). After t=4000, the yellow particle in the outer leaflet surpasses the blue particle in the inner leaflet by the distance about 1 particle diameter. This movie includes the simulation results for 4 μs.

Download Fu et al. Supplementary Movie 3(Video)
Video 6.3 MB

Fu et al. Supplementary Movie 4

The numerical results show that the JP vesicle ruptures at the shear rate χ=0.0655. The colored field from dark blue to dark red shows the hydrophobic attraction activity and the range is from 0 to 1. All white dots in the domain are tracers in fluid that move with the fluid motion. This movie includes the simulation results for 0.6 μs.

Download Fu et al. Supplementary Movie 4(Video)
Video 6.1 MB

Fu et al. Supplementary Movie 5

There are two relaxed JP vesicles suspended in a shear flow. The two centroids are at coordinates (-25,0) and (25,0) in nm. The colored field from dark blue to dark red shows the hydrophobic attraction activity and the range is from 0 to 1. All white dots in the domain are tracers in fluid that move with the fluid motion. This movie includes the simulation results for 4 μs.

Download Fu et al. Supplementary Movie 5(Video)
Video 31.6 MB

Fu et al. Supplementary Movie 6

There are two relaxed JP vesicles suspended in an extensional flow. The centroid of the left JP vesicle is 0.25 nm above the x-axis and the right JP vesicle is 0.25 nm below the x-axis. The colored field from dark blue to dark red shows the hydrophobic attraction activity and the range is from 0 to 1. All white dots in the domain are tracers in fluid that move with the fluid motion. This movie includes the simulation results for 1.2 μs.

Download Fu et al. Supplementary Movie 6(Video)
Video 7.3 MB