Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-13T05:11:22.119Z Has data issue: false hasContentIssue false
  • English
  • Français

Two-dimensional planar plumes and fountains

Published online by Cambridge University Press:  04 June 2014

T. S. van den Bremer Open the ORCID record for T. S. van den Bremer [Opens in a new window]  and
G. R. Hunt
T. S. van den Bremer*
Affiliation:
Department of Engineering Science, University of Oxford, Parks Road, Oxford OX1 3PJ, UK
G. R. Hunt*
Affiliation:
Department of Engineering, University of Cambridge, Trumpington Street, Cambridge CB2 1PZ, UK
*
†Email addresses for correspondence: ton.vandenbremer@eng.ox.ac.uk, gary.hunt@eng.cam.ac.uk
†Email addresses for correspondence: ton.vandenbremer@eng.ox.ac.uk, gary.hunt@eng.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

Closed-form solutions describing the behaviour of two-dimensional planar turbulent rising plumes and fountains from horizontal planar area and line sources in unconfined quiescent environments of uniform density are proposed. Extending the analysis on axisymmetric releases by van den Bremer & Hunt (J. Fluid Mech., vol. 644, 2010, pp. 165–192) to planar releases, the local flux balance parameter 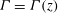$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}\varGamma =\varGamma (z)$ is instrumental in describing the bulk behaviour of steady Boussinesq and non-Boussinesq planar plumes and the initial rise behaviour of Boussinesq planar fountains as a function of height $z$. Expressions for the asymptotic virtual source correction are developed and the results elucidated by ‘scale diagrams’ (cf. Morton & Middleton, J. Fluid Mech., vol. 58, 1973, pp. 165–176) showing certain characteristic heights for different source conditions. These diagrams capture all the different manifestations of plume behaviour, encompassing fountains, jets, source-momentum-dominated or ‘forced’ plumes, pure plumes and source-buoyancy-dominated or ‘lazy’ plumes, and their associated key features. Other flow features identified include a gravity-driven deceleration regime and a mixing-driven regime for forced fountains. Deceleration in lazy fountains is purely gravity-driven. The results can be shown to be valid for both Boussinesq and non-Boussinesq plumes (but not for non-Boussinesq fountains) thus resulting in universal solutions valid for both cases provided the entrainment velocity is unaffected by non-Boussinesq effects. This paper presents and explores these universal solutions. An accompanying paper (van den Bremer & Hunt, J. Fluid Mech., vol. 750, 2014, pp. 245–258) examines the implications for non-Boussinesq plumes. The existing solutions of Lee & Emmons (J. Fluid Mech., vol. 11, 1961, pp. 353–368) generalized herein are valid for a constant entrainment coefficient $\alpha $. New results for an entrainment coefficient that varies linearly with 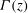$\varGamma (z)$ and thus captures experimental values far more realistically are presented for forced plumes.

JFM classification

Convection: Convection Convection: Plumes/thermals
Type
Papers
Information
Journal of Fluid Mechanics , Volume 750 , 10 July 2014 , pp. 210 - 244
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Antonia, R. A., Browne, L. W. B., Rajagopalan, S. & Chambers, A. J. 1983 On the organized motion of a turbulent plane jet. J. Fluid Mech. 134, 49–66.Google Scholar
van den Bremer, T. S. & Hunt, G. R. 2010 Universal solutions for Boussinesq and non-Boussinesq plumes. J. Fluid Mech. 644, 165–192.CrossRefGoogle Scholar
van den Bremer, T. S. & Hunt, G. R. 2014 Two-dimensional planar plumes: non-Boussinesq effects. J. Fluid Mech. 750, 245–258.Google Scholar
Bush, J. W. M. & Woods, A. W. 1999 Vortex generation by line plumes in a rotating stratified fluid. J. Fluid Mech. 388, 289–313.Google Scholar
Campbell, A. N. & Cardoso, S. S. S. 2010 Turbulent plumes with internal generation of buoyancy by chemical reaction. J. Fluid Mech. 655, 122–151.CrossRefGoogle Scholar
Chen, C. J. & Rodi, W. 1980 Vertical Turbulent Buoyant Jets, A Review of Experimental Data. Pergamon.Google Scholar
Ching, C. Y., Fernando, H. J. S. & Noh, Y. 1993 Interaction of a negatively buoyant line plume with a density interface. Dyn. Atmos. Oceans 19 (1), 367–388.Google Scholar
Conroy, D. T. & Llewellyn Smith, S. G. 2008 Endothermic and exothermic chemically-reacting plumes. J. Fluid Mech. 612, 291–310.Google Scholar
Delichatsios, M. A. 1988 On the similarity of velocity and temperature profiles in strong (variable density) turbulent buoyant plumes. Combust. Sci. Technol. 60, 253–266.Google Scholar
Fischer, H. B., List, E. J., Koh, R. C. Y., Imberger, J. & Brooks, N. H.(Eds) 1979 Mixing in Inland and Coastal Waters. Academic.Google Scholar
Hunt, G. R. & van den Bremer, T. S. 2011 Classical plume theory: 1937–2010 and beyond. IMA J. Appl. Maths 76 (3), 424–448.CrossRefGoogle Scholar
Hunt, G. R. & Coffey, C. J. 2009 Characterising line fountains. J. Fluid Mech. 623, 317–327.Google Scholar
Hunt, G. R. & Kaye, N. B. 2005 Lazy plumes. J. Fluid Mech. 533, 329–338.Google Scholar
Jirka, G. H. 2006 Integral model for turbulent buoyant jets in unbounded stratified flows part 2: plane jet dynamics resulting from multiport diffuser jets. Environ. Fluid Mech. 6 (1), 43–100.Google Scholar
Kaminski, E., Tait, S. & Carazzo, G. 2005 Turbulent entrainment in jets with arbitrary buoyancy. J. Fluid Mech. 526, 361–376.Google Scholar
Kay, A. 2007 Warm discharges in cold fresh water. Part 1. Line plumes in a uniform environment. J. Fluid Mech. 574, 239–271.Google Scholar
Kaye, N. B. 2008 Turbulent plumes in stratified environments: a review of recent work. Atmos. Ocean 46, 433–441.Google Scholar
Kaye, N. B. & Hunt, G. R. 2009 An experimental study of large area source turbulent plumes. Intl J. Heat Fluid Flow 30, 1099–1105.Google Scholar
Kaye, N. B. & Scase, M. M. 2011 Straight-sided solutions to classical and modified plume equations. J. Fluid Mech. 680, 564–573.Google Scholar
Koh, R. C. Y. & Brooks, N. H. 1975 The fluid mechanics of waste-water disposal in the ocean. Annu. Rev. Fluid Mech. 7, 187–211.CrossRefGoogle Scholar
Kotsovinos, N. E.1975 A study of the entrainment and turbulence in a plane buoyant jet. PhD thesis, California Institute of Technology.Google Scholar
Kotsovinos, N. E. 1976 A note on the spreading rate and virtual origin of a plane turbulent jet. J. Fluid Mech. 77, 305–311.Google Scholar
Kotsovinos, N. E. & List, E. J. 1977 Plane turbulent buoyant jets. Part 1. Integral properties. J. Fluid Mech. 81, 25–44.Google Scholar
Lee, S.-H. & Emmons, H. W. 1961 A study of natural convection above a line fire. J. Fluid Mech. 11, 353–368.Google Scholar
Linden, P. F. 2000 Convection in the environment. In Perspectives in Fluid Dynamics: A Collective Introduction to Current Research (ed. Batchelor, G. K., Moffatt, H. K. & Worster, M. G.), Cambridge University Press.Google Scholar
List, E. J. & Imberger, J. 1973 Turbulent entrainment in buoyant jets and plumes. J. Hydraul. Div. ASCE 99, 1461–1474.Google Scholar
Mehaddi, R., Vauquelin, O. & Candelier, F. 2012 Analytical solutions for turbulent Boussinesq fountains in a linearly stratified environment. J. Fluid Mech. 691, 487–497.Google Scholar
Morton, B. R. 1959 Forced plumes. J. Fluid Mech. 5, 151–163.Google Scholar
Morton, B. R. & Middleton, J. 1973 Scale diagrams for forced plumes. J. Fluid Mech. 58, 165–176.Google Scholar
Morton, B. R., Taylor, G. I. & Turner, J. S. 1956 Turbulent gravitational convection from maintained and instantaneous sources. Proc. R. Soc. Lond. A 234, 1–23.Google Scholar
Priestley, C. H. B. & Ball, F. K. 1955 Continuous convection from an isolated source of heat. Q. J. R. Meteorol. Soc. 81, 144–157.Google Scholar
Radomski, S.2008 Natural ventilation of enclosures driven by sources of buoyancy at different elevations. PhD thesis, Imperial College London, UK.Google Scholar
Rooney, G. G.1997 Buoyant flows from fires in enclosures. PhD thesis, University of Cambridge, UK.Google Scholar
Rooney, G. G. & Linden, P. F. 1996 Similarity considerations for non-Boussinesq plumes in an unstratified environment. J. Fluid Mech. 318, 237–250.CrossRefGoogle Scholar
Rouse, H., Yih, C. S. & Humphreys, H. W. 1952 Gravitational convection from a boundary source. Tellus 4, 201–210.Google Scholar
Scase, M. M., Caulfield, C. P., Dalziel, S. B. & Hunt, J. C. R. 2006 Time-dependent plumes and jets with decreasing source strengths. J. Fluid Mech. 563, 431–461.Google Scholar
Taylor, G. I.1945 Dynamics of a mass of hot gas rising in air. US Atomic Energy Commission MDDC 919. LADC 276.Google Scholar
Thomas, P. J. & Delichatsios, M. A. 2007 Notes on the similarity of turbulent buoyant fire plumes with large density variations. Fire Safety J. 42, 43–50.CrossRefGoogle Scholar
Turner, J. S. 1966 Jets and plumes with negative or reversing buoyancy. J. Fluid Mech. 26, 779–792.Google Scholar
Wettlaufer, J. S., Worster, M. G. & Huppert, H. E. 1997 Natural convection during solidification of an alloy from above with application to the evolution of sea ice. J. Fluid Mech. 344, 291–316.Google Scholar
Widell, K., Fer, I. & Haugan, P. M. 2006 Salt release from warming sea ice. Geophys. Res. Lett. 33, L12501.CrossRefGoogle Scholar
Woods, A. W. 1997 A note on non-Boussinesq plumes in an incompressible stratified environment. J. Fluid Mech. 345, 347–356.Google Scholar
Woods, A. W. 2010 Turbulent plumes in nature. Annu. Rev. Fluid Mech. 42, 391–412.Google Scholar
Yuan, L. M. & Cox, G. 1996 An experimental study of some fire lines. Fire Safety J. 27, 123–139.CrossRefGoogle Scholar