Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-28T03:50:21.715Z Has data issue: false hasContentIssue false
  • English
  • Français

Uncoupling the effects of aspect ratio, Reynolds number and Rossby number on a rotating insect-wing planform

Published online by Cambridge University Press:  26 November 2018

Shantanu S. Bhat Open the ORCID record for Shantanu S. Bhat [Opens in a new window] ,
Jisheng Zhao ,
John Sheridan ,
Kerry Hourigan  and
Mark C. Thompson
Shantanu S. Bhat*
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Jisheng Zhao
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
John Sheridan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Kerry Hourigan
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
Mark C. Thompson
Affiliation:
Fluids Laboratory for Aeronautical and Industrial Research (FLAIR), Department of Mechanical and Aerospace Engineering, Monash University, Melbourne, VIC 3800, Australia
*
†Email address for correspondence: shantanu.bhat@monash.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

The individual and combined influences of aspect ratio (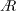$A$), Reynolds number (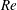$Re$) and Rossby number (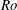$Ro$) on the leading-edge vortex (LEV) of a rotating wing of insect-like planform are investigated numerically. A previous study from our group has determined the wingspan to be an appropriate length scale governing the large-scale LEV structure. In this study, the 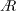$A$ range considered is further extended, to show that this scaling works well as 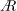$A$ is varied by a factor of 4 (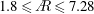$1.8\leqslant A\leqslant 7.28$) and over a 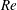$Re$ range of two orders of magnitude. The present study also extends this scaling for wings with an offset from the rotation axis, which is typically the case for actual insects and often for experiments. Remarkably, the optimum range of 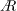$A$ based on the lift coefficients at different $Re$ coincides with that observed in nature. The scaling based on the wingspan is extended to the acceleration terms of the Navier–Stokes equations, suggesting a modified scaling of 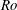$Ro$, which decouples the effects of 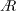$A$. A detailed investigation of the flow structures, by increasing 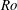$Ro$ in a wide range, reveals the weakening of the LEV due to the reduced spanwise flow, resulting in a reduced lift. Overall, the use of span-based scaling of $Re$ and $Ro$, together with $A$, may help reconcile apparent conflicting trends between observed variations in aerodynamic performance in different sets of experiments and simulations.

JFM classification

Aerodynamics: Aerodynamics Biological Fluid Dynamics: Biological Fluid Dynamics Biological Fluid Dynamics: Swimming/flying
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 859 , 25 January 2019 , pp. 921 - 948
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ansari, S. A., Knowles, K. & Zbikowski, R. 2008 Insectlike flapping wings in the hover. Part II. Effect of wing geometry. J. Aircraft 45 (6), 1976–1990.Google Scholar
Bhat, S. S., Zhao, J., Sheridan, J., Hourigan, K. & Thompson, M. C. 2018 The leading-edge vortex on a rotating wing changes markedly beyond a certain central body size. R. Soc. Open Sci. 5 (7), 172197.Google Scholar
Birch, J. M. & Dickinson, M. H. 2001 Spanwise flow and the attachment of the leading-edge vortex on insect wings. Nature 412, 729–733.Google Scholar
Birch, J. M., Dickson, W. B. & Dickinson, M. H. 2004 Force production and flow structure of the leading edge vortex on flapping wings at high and low Reynolds numbers. J. Expl Biol. 207 (7), 1063–1072.Google Scholar
Carr, Z. R., Devoria, A. C. & Ringuette, M. J. 2015 Aspect-ratio effects on rotating wings: circulation and forces. J. Fluid Mech. 767, 497–525.Google Scholar
Dickinson, M. H., Lehmann, F.-O. & Sane, S. P. 1999 Wing rotation and the aerodynamic basis of insect flight. Science 284 (5422), 1954–1960.Google Scholar
Ellington, C. P. 1984 The aerodynamics of hovering insect flight. II. Morphological parameters. Phil. Trans. R. Soc. Lond. B 305 (1122), 17–40.Google Scholar
Ellington, C. P., van den Berg, C., Willmott, A. P. & Thomas, A. L. R. 1996 Leading-edge vortices in insect flight. Nature 384 (6610), 626–630.Google Scholar
Garmann, D. J. & Visbal, M. R. 2014 Dynamics of revolving wings for various aspect ratios. J. Fluid Mech. 748, 932–956.Google Scholar
Graftieaux, L., Michard, M. & Grosjean, N. 2001 Combining PIV, POD and vortex identification algorithms for the study of unsteady turbulent swirling flows. Meas. Sci. Technol. 12 (9), 1422–1429.Google Scholar
Han, J.-S., Chang, J. W. & Cho, H.-K. 2015 Vortices behavior depending on the aspect ratio of an insect-like flapping wing in hover. Exp. Fluids 56 (9), 181.Google Scholar
Harbig, R. R., Sheridan, J. & Thompson, M. C. 2013 Reynolds number and aspect ratio effects on the leading-edge vortex for rotating insect wing planforms. J. Fluid Mech. 717, 166–192.Google Scholar
Harbig, R. R., Sheridan, J., Thompson, M. C., Ozen, C. A. & Rockwell, D.2012 Observations of flow structure changes with aspect ratio for rotating insect wing planforms. In 42nd AIAA Fluid Dynamics Conference and Exhibit. AIAA Paper 2012-3282.Google Scholar
Hawkes, E. W. & Lentink, D. 2016 Fruit fly scale robots can hover longer with flapping wings than with spinning wings. J. R. Soc. Interface 13 (123), 20160730.Google Scholar
Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. In Center for Turbulence Research, Proceedings of the Summer Program, pp. 193–208.Google Scholar
Jardin, T. 2017 Coriolis effect and the attachment of the leading edge vortex. J. Fluid Mech. 820, 312–340.Google Scholar
Jardin, T. & Colonius, T. 2018 On the lift-optimal aspect ratio of a revolving wing at low Reynolds number. J. R. Soc. Interface 15 (143), 20170933.Google Scholar
Kim, D. & Gharib, M. 2010 Experimental study of three-dimensional vortex structures in translating and rotating plates. Exp. Fluids 49 (1), 329–339.Google Scholar
Kruyt, J. W., van Heijst, G. F., Altshuler, D. L. & Lentink, D. 2015 Power reduction and the radial limit of stall delay in revolving wings of different aspect ratio. J. R. Soc. Interface 12, 20150051.Google Scholar
Lee, Y. J., Lua, K. B. & Lim, T. T. 2016 Aspect ratio effects on revolving wings with Rossby number consideration. Bioinspir. Biomim. 11 (5), 056013.Google Scholar
Lentink, D. & Dickinson, M. H. 2009a Biofluiddynamic scaling of flapping, spinning and translating fins and wings. J. Expl Biol. 212 (16), 2691–2704.Google Scholar
Lentink, D. & Dickinson, M. H. 2009b Rotational accelerations stabilize leading edge vortices on revolving fly wings. J. Expl Biol. 212 (16), 2705–2719.Google Scholar
Limacher, E., Morton, C. & Wood, D. 2016 On the trajectory of leading-edge vortices under the influence of Coriolis acceleration. J. Fluid Mech. 800, R1.Google Scholar
Liu, H. & Aono, H. 2009 Size effects on insect hovering aerodynamics: an integrated computational study. Bioinspir. Biomim. 4 (1), 15002.Google Scholar
Luo, G. & Sun, M. 2005 The effects of corrugation and wing planform on the aerodynamic force production of sweeping model insect wings. Acta Mechanica Sin. 21 (6), 531–541.Google Scholar
Maxworthy, T. 1979 Experiments on the Weis–Fogh mechanism of lift generation by insects in hovering flight. Part 1. Dynamics of the ‘fling’. J. Fluid Mech. 93, 47–63.Google Scholar
Ozen, C. A. & Rockwell, D. 2012 Three-dimensional vortex structure on a rotating wing. J. Fluid Mech. 707, 541–550.Google Scholar
Ozen, C. A. & Rockwell, D.2013 Flow structure on a rotating wing: effect of wing aspect ratio and shape. In 51st AIAA Aerospace Sciences Meeting. AIAA Paper 2013-676.Google Scholar
Phillips, N., Knowles, K. & Bomphrey, R. J. 2015 The effect of aspect ratio on the leading-edge vortex over an insect-like flapping wing. Bioinspir. Biomim. 10 (5), 056020.Google Scholar
Phillips, N., Knowles, K. & Bomphrey, R. J. 2017 Petiolate wings: effects on the leading-edge vortex in flapping flight. Interface Focus 7, 20160084.Google Scholar
Poelma, C., Dickson, W. B. & Dickinson, M. H. 2006 Time-resolved reconstruction of the full velocity field around a dynamically-scaled flapping wing. Exp. Fluids 41 (2), 213–225.Google Scholar
Sane, S. P. & Dickinson, M. H. 2002 The aerodynamic effects of wing rotation and a revised quasi-steady model of flapping flight. J. Expl Biol. 205, 1087–1096.Google Scholar
Shahzad, A., Tian, F. B., Young, J. & Lai, J. C. S. 2016 Effects of wing shape, aspect ratio and deviation angle on aerodynamic performance of flapping wings in hover. Phys. Fluids 28 (11), 111901.Google Scholar
Shyy, W. & Liu, H. 2007 Flapping wings and aerodynamic lift: the role of leading-edge vortices. AIAA J. 45 (12), 2817–2819.Google Scholar
Tudball Smith, D., Rockwell, D., Sheridan, J. & Thompson, M. 2017 Effect of radius of gyration on a wing rotating at low Reynolds number: a computational study. Phys. Rev. Fluids 2 (6), 064701.Google Scholar
Usherwood, J. R. & Ellington, C. P. 2002 The aerodynamics of revolving wings II. Propeller force coefficients from mayfly to quail. J. Expl Biol. 205 (11), 1565–1576.Google Scholar
Vogel, S. 1966 Flight in Drosophila I. Flight performance of tethered flies. J. Expl Biol. 44, 567–578.Google Scholar
Weis-Fogh, T. 1973 Quick estimates of flight fitness in hovering animals, including novel mechanisms for lift production. J. Expl Biol. 59 (1), 169–230.Google Scholar
Wolfinger, M. & Rockwell, D. 2014 Flow structure on a rotating wing: effect of radius of gyration. J. Fluid Mech. 755, 83–110.Google Scholar
Zanker, J. M. & Götz, K. G. 1990 The wing beat of Drosophila melanogaster. II. Dynamics. Phil. Trans. R. Soc. Lond. B 327 (1238), 19–44.Google Scholar

Bhat et al. supplementary movie

A comparison of the temporal evolution of the flow structures over the wings of aspect ratios 7.28 and 2.91 rotating at the span based Reynolds number of 300 is shown. The top row shows the comparison at constant Rg/c, whereas the left column shows the comparison at constant Rg/b, in which the AR=7.28 wing is common. Phi represents the rotation phase of the wing. The vortices are identified by the isosurfaces of the constant Q criterion.

Download Bhat et al. supplementary movie(Video)
Video 2.3 MB