Article contents
Understanding discrete capillary-wave turbulence using a quasi-resonant kinetic equation
Published online by Cambridge University Press: 06 March 2017
Abstract
Experimental and numerical studies have shown that, with sufficient nonlinearity, the theoretical capillary-wave power-law spectrum derived from the kinetic equation (KE) of weak turbulence theory can be realized. This is despite the fact that the KE is derived assuming an infinite domain with continuous wavenumber, while experiments and numerical simulations are conducted in realistic finite domains with discrete wavenumbers for which the KE theoretically allows no energy transfer. To understand this, we first analyse results from direct simulations of the primitive Euler equations to elucidate the role of nonlinear resonance broadening (NRB) in discrete turbulence. We define a quantitative measure of the NRB, explaining its dependence on the nonlinearity level and its effect on the properties of the obtained stationary power-law spectra. This inspires us to develop a new quasi-resonant kinetic equation (QKE) for discrete turbulence, which incorporates the mechanism of NRB, governed by a single parameter  $\unicode[STIX]{x1D705}$ expressing the ratio of NRB and wavenumber discreteness. At
$\unicode[STIX]{x1D705}$ expressing the ratio of NRB and wavenumber discreteness. At 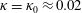 $\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{0}\approx 0.02$, the QKE recovers simultaneously the spectral slope
$\unicode[STIX]{x1D705}=\unicode[STIX]{x1D705}_{0}\approx 0.02$, the QKE recovers simultaneously the spectral slope 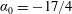 $\unicode[STIX]{x1D6FC}_{0}=-17/4$ and the Kolmogorov constant
$\unicode[STIX]{x1D6FC}_{0}=-17/4$ and the Kolmogorov constant 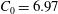 $C_{0}=6.97$ (corrected from the original derivation) of the theoretical continuous spectrum, which physically represents the upper bound of energy cascade capacity for the discrete turbulence. For
$C_{0}=6.97$ (corrected from the original derivation) of the theoretical continuous spectrum, which physically represents the upper bound of energy cascade capacity for the discrete turbulence. For 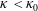 $\unicode[STIX]{x1D705}<\unicode[STIX]{x1D705}_{0}$, the obtained spectra represent those corresponding to a finite domain with insufficient nonlinearity, resulting in a steeper spectral slope
$\unicode[STIX]{x1D705}<\unicode[STIX]{x1D705}_{0}$, the obtained spectra represent those corresponding to a finite domain with insufficient nonlinearity, resulting in a steeper spectral slope 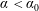 $\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{0}$ and reduced capacity of energy cascade
$\unicode[STIX]{x1D6FC}<\unicode[STIX]{x1D6FC}_{0}$ and reduced capacity of energy cascade 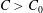 $C>C_{0}$. The physical insights from the QKE are corroborated by direct simulation results of the Euler equations.
$C>C_{0}$. The physical insights from the QKE are corroborated by direct simulation results of the Euler equations.
- Type
- Rapids
- Information
- Copyright
- © 2017 Cambridge University Press
References
- 23
- Cited by



