Hostname: page-component-78c5997874-ndw9j Total loading time: 0 Render date: 2024-11-10T07:01:15.771Z Has data issue: false hasContentIssue false
  • English
  • Français

Understanding liquid-jet atomization cascades via vortex dynamics

Published online by Cambridge University Press:  21 March 2018

A. Zandian Open the ORCID record for A. Zandian [Opens in a new window] ,
W. A. Sirignano Open the ORCID record for W. A. Sirignano [Opens in a new window]  and
F. Hussain Open the ORCID record for F. Hussain [Opens in a new window]
A. Zandian
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
W. A. Sirignano*
Affiliation:
Department of Mechanical and Aerospace Engineering, University of California, Irvine, CA 92697, USA
F. Hussain
Affiliation:
Department of Mechanical Engineering, Texas Tech University, Lubbock, TX 79409, USA
*
†Email address for correspondence: sirignan@uci.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

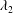Temporal instabilities of a planar liquid jet are studied using direct numerical simulation (DNS) of the incompressible Navier–Stokes equations with level-set (LS) and volume-of-fluid (VoF) surface tracking methods. $\unicode[STIX]{x1D706}_{2}$ contours are used to relate the vortex dynamics to the surface dynamics at different stages of the jet breakup – namely, lobe formation, lobe perforation, ligament formation, stretching and tearing. Three distinct breakup mechanisms are identified in the primary breakup, which are well categorized on the parameter space of gas Weber number (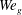$We_{g}$) versus liquid Reynolds number (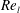$Re_{l}$). These mechanisms are analysed here from a vortex dynamics perspective. Vortex dynamics explains the hairpin formation, and the interaction between the hairpins and the Kelvin–Helmholtz (KH) roller explains the perforation of the lobes, which is attributed to the streamwise overlapping of two oppositely oriented hairpin vortices on top and bottom of the lobe. The formation of corrugations on the lobe front edge at high 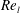$Re_{l}$ is also related to the location and structure of the hairpins with respect to the KH vortex. The lobe perforation and corrugation formation are inhibited at low 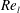$Re_{l}$ and low 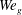$We_{g}$ due to the high surface tension and viscous forces, which damp the small-scale corrugations and resist hole formation. Streamwise vorticity generation – resulting in three-dimensional instabilities – is mainly caused by vortex stretching and baroclinic torque at high and low density ratios, respectively. Generation of streamwise vortices and their interaction with spanwise vortices produce the liquid structures seen at various flow conditions. Understanding the liquid sheet breakup and the related vortex dynamics are crucial for controlling the droplet-size distribution in primary atomization.

JFM classification

Multiphase and Particle-laden Flows: Gas/liquid flow Vortex Flows: Vortex dynamics Vortex Flows: Vortex interactions
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 843 , 25 May 2018 , pp. 293 - 354
Copyright
© 2018 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Agbaglah, G., Chiodi, R. & Desjardins, O. 2017 Numerical simulation of the initial destabilization of an air-blasted liquid layer. J. Fluid Mech. 812, 1024–1038.Google Scholar
Agbaglah, G., Josserand, C. & Zaleski, S. 2013 Longitudinal instability of a liquid rim. Phys. Fluids 25 (2), 022103.Google Scholar
Ashurst, W. T. & Meiburg, E. 1988 Three-dimensional shear layers via vortex dynamics. J. Fluid Mech. 189, 87–116.Google Scholar
Bernal, L. P. & Roshko, A. 1986 Streamwise vortex structure in plane mixing layers. J. Fluid Mech. 170, 499–525.Google Scholar
Brancher, P., Chomaz, J. M. & Huerre, P. 1994 Direct numerical simulations of round jets: vortex induction and side jets. Phys. Fluids 6 (5), 1768–1774.Google Scholar
Breidenthal, R. 1981 Structure in turbulent mixing layers and wakes using a chemical reaction. J. Fluid Mech. 109, 1–24.Google Scholar
Collis, S. S., Lele, S. K., Moser, R. D. & Rogers, M. M. 1994 The evolution of a plane mixing layer with spanwise nonuniform forcing. Phys. Fluids 6 (1), 381–396.Google Scholar
Comte, P., Lesieur, M. & Lamballais, E. 1992 Large-and small-scale stirring of vorticity and a passive scalar in a 3-D temporal mixing layer. Phys. Fluids A 4 (12), 2761–2778.Google Scholar
Dabiri, S., Sirignano, W. A. & Joseph, D. D. 2007 Cavitation in an orifice flow. Phys. Fluids 19 (7), 072112.Google Scholar
Danaila, I., Dušek, J. & Anselmet, F. 1997 Coherent structures in a round, spatially evolving, unforced, homogeneous jet at low Reynolds numbers. Phys. Fluids 9 (11), 3323–3342.Google Scholar
Desjardins, O. & Pitsch, H. 2010 Detailed numerical investigation of turbulent atomization of liquid jets. Atomiz. Sprays 20 (4), 311–336.Google Scholar
Dimotakis, P. 1986 Two-dimensional shear-layer entrainment. AIAA J. 24 (11), 1791–1796.Google Scholar
Fuster, D., Matas, J.-P., Marty, S., Popinet, S., Hoepffner, J., Cartellier, A. & Zaleski, S. 2013 Instability regimes in the primary breakup region of planar coflowing sheets. J. Fluid Mech. 736, 150–176.Google Scholar
Gaster, M. 1962 A note on the relation between temporally-increasing and spatially-increasing disturbances in hydrodynamic stability. J. Fluid Mech. 14 (2), 222–224.Google Scholar
Herrmann, M. 2011 On simulating primary atomization using the refined level set grid method. Atomiz. Sprays 21 (4), 283–301.Google Scholar
Hirt, C. W. & Nichols, B. D. 1981 Volume of fluid (VOF) method for the dynamics of free boundaries. J. Comput. Phys. 39 (1), 201–225.Google Scholar
Hoepffner, J., Blumenthal, R. & Zaleski, S. 2011 Self-similar wave produced by local perturbation of the Kelvin–Helmholtz shear-layer instability. Phys. Rev. Lett. 106 (10), 104502.Google Scholar
Hussain, A. K. M. F. 1986 Coherent structures and turbulence. J. Fluid Mech. 173, 303–356.Google Scholar
Jarrahbashi, D. & Sirignano, W. A. 2014 Vorticity dynamics for transient high-pressure liquid injection. Phys. Fluids 26 (10), 101304.Google Scholar
Jarrahbashi, D., Sirignano, W. A., Popov, P. P. & Hussain, F. 2016 Early spray development at high gas density: hole, ligament and bridge formations. J. Fluid Mech. 792, 186–231.Google Scholar
Jeong, J. & Hussain, F. 1995 On the identification of a vortex. J. Fluid Mech. 285, 69–94.Google Scholar
Jimenez, J. 1983 A spanwise structure in the plane shear layer. J. Fluid Mech. 132, 319–336.Google Scholar
Kolář, V. 2007 Vortex identification: new requirements and limitations. Intl J. Heat Fluid Flow 28 (4), 638–652.Google Scholar
Lasheras, J. C. & Choi, H. 1988 Three-dimensional instability of a plane free shear layer: an experimental study of the formation and evolution of streamwise vortices. J. Fluid Mech. 189, 53–86.Google Scholar
Lefebvre, A. H. 1989 Atomization and Sprays, vol. 1989. Hemisphere Publishing Corp.Google Scholar
Liepmann, D. & Gharib, M. 1992 The role of streamwise vorticity in the near-field entrainment of round jets. J. Fluid Mech. 245, 643–668.Google Scholar
Ling, Y., Fuster, D., Zaleski, S. & Tryggvason, G. 2017 Spray formation in a quasiplanar gas–liquid mixing layer at moderate density ratios: a numerical closeup. Phys. Rev. Fluids 2 (1), 014005.Google Scholar
Marmottant, P. & Villermaux, E. 2004 On spray formation. J. Fluid Mech. 498, 73–111.Google Scholar
Martin, J. E. & Meiburg, E. 1991 Numerical investigation of three-dimensionally evolving jets subject to axisymmetric and azimuthal perturbations. J. Fluid Mech. 230, 271–318.Google Scholar
Matas, J.-P., Marty, S. & Cartellier, A. 2011 Experimental and analytical study of the shear instability of a gas–liquid mixing layer. Phys. Fluids 23 (9), 094112.Google Scholar
Ohnesorge, W. V. 1936 Die Bildung von Tropfen an Düsen und die Auflösung flüssiger Strahlen. Z. Angew. Math. Mech. 16 (6), 355–358.Google Scholar
Osher, S. & Fedkiw, R. P. 2001 Level set methods: an overview and some recent results. J. Comput. Phys. 169 (2), 463–502.Google Scholar
Otto, T., Rossi, M. & Boeck, T. 2013 Viscous instability of a sheared liquid-gas interface: dependence on fluid properties and basic velocity profile. Phys. Fluids 25 (3), 032103.Google Scholar
Pope, S. B. 1978 An explanation of the turbulent round-jet/plane-jet anomaly. AIAA J. 16 (3), 279–281.Google Scholar
Pradeep, D. S. & Hussain, F. 2006 Transient growth of perturbations in a vortex column. J. Fluid Mech. 550, 251–288.Google Scholar
Reitz, R. D. & Bracco, F. V. 1986 Mechanisms of breakup of round liquid jets. Encyclopedia Fluid Mech. 3, 233–249.Google Scholar
Rider, W. J. & Kothe, D. B. 1998 Reconstructing volume tracking. J. Comput. Phys. 141 (2), 112–152.Google Scholar
Scardovelli, R. & Zaleski, S. 1999 Direct numerical simulation of free-surface and interfacial flow. Annu. Rev. Fluid Mech. 31 (1), 567–603.Google Scholar
Schoppa, W., Hussain, F. & Metcalfe, R. W. 1995 A new mechanism of small-scale transition in a plane mixing layer: core dynamics of spanwise vortices. J. Fluid Mech. 298, 23–80.Google Scholar
Schowalter, D. G., Van Atta, C. W. & Lasheras, J. C. 1994 Baroclinic generation of streamwise vorticity in a stratified shear layer. Meccanica 29 (4), 361–371.Google Scholar
Shinjo, J. & Umemura, A. 2010 Simulation of liquid jet primary breakup: dynamics of ligament and droplet formation. Intl J. Multiphase Flow 36 (7), 513–532.Google Scholar
Sussman, M., Fatemi, E., Smereka, P. & Osher, S. 1998 An improved level set method for incompressible two-phase flows. Comput. Fluids 27 (5), 663–680.Google Scholar
Widnall, S. E., Bliss, D. B. & Tsai, C. Y. 1974 The instability of short waves on a vortex ring. J. Fluid Mech. 66 (01), 35–47.Google Scholar
Widnall, S. E. & Sullivan, J. P. 1973 On the stability of vortex rings. Proc. R. Soc. Lond. A 332 (1590), 335–353.Google Scholar
Zandian, A., Sirignano, W. A. & Hussain, F.2016 Three-dimensional liquid sheet breakup: vorticity dynamics. AIAA Paper 2016-1593.Google Scholar
Zandian, A., Sirignano, W. A. & Hussain, F. 2017 Planar liquid jet: early deformation and atomization cascades. Phys. Fluids 29 (6), 062109.Google Scholar
Zhao, H. K., Chan, T., Merriman, B. & Osher, S. 1996 A variational level set approach to multiphase motion. J. Comput. Phys. 127 (1), 179–195.Google Scholar
Zuzio, D., Estivalèzes, J.-L. & Dipierro, B. 2016 An improved multiscale Eulerian–Lagrangian method for simulation of atomization process. Comput. Fluids; https://doi.org/10.1016/j.compfluid.2016.12.018.Google Scholar