Article contents
Unravelling the Rayleigh–Taylor instability by stabilization
Published online by Cambridge University Press: 12 September 2013
Abstract
A recently proposed stabilization mechanism for the Rayleigh–Taylor instability, using magnetic fluids and azimuthally rotating magnetic fields, is experimentally investigated in a cylindrical geometry and compared with the theoretical model. This approach allows the imperfection of the experimental setup to be exploited for measuring the critical field strength of the instability without ever reaching the supercritical state. Furthermore, we use a fast increase in the magnetic field strength to prevent an already occurring instability and force the system back to its initial state. In this way we measure the growth dynamics repeatedly and acquire the characteristic time scale 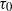 ${\tau }_{0} $ of the instability.
${\tau }_{0} $ of the instability.
JFM classification
Information
- Type
- Rapids
- Information
- Creative Commons
- The online version of this article is published within an Open Access environment subject to the conditions of the Creative Commons Attribution licence .
- Copyright
- ©2013 Cambridge University Press.
References
- 7
- Cited by

