Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Kou, Jiaqing
and
Zhang, Weiwei
2021.
Data-driven modeling for unsteady aerodynamics and aeroelasticity.
Progress in Aerospace Sciences,
Vol. 125,
Issue. ,
p.
100725.
Xiao, Qianhao
Shi, Xuna
Wu, Linghui
Wang, Jun
Ding, Yanyan
and
Jiang, Boyan
2021.
Squirrel-Cage Fan System Optimization and Flow Field Prediction Using Parallel Filling Criterion and Surrogate Model.
Processes,
Vol. 9,
Issue. 9,
p.
1620.
Rocha Ribeiro, Bernardo Luiz
and
Franck, Jennifer A.
2021.
A Machine Learning Approach to Classify Kinematics and Vortex Wake Modes of Oscillating Foils.
Price, Theron J.
Gragston, Mark
and
Kreth, Phillip A.
2022.
Analysis of Screech Phenomena in a Mach 1.0 Jet with Linear Array Focused Laser Differential Interferometry.
Brown, Justin
Zimny, Jacqueline
and
Radko, Timour
2022.
Identifying the Origin of Turbulence Using Convolutional Neural Networks.
Fluids,
Vol. 7,
Issue. 7,
p.
239.
Zhou, Zhideng
Li, Binglin
Yang, Xiaolei
and
Yang, Zixuan
2022.
A robust super-resolution reconstruction model of turbulent flow data based on deep learning.
Computers & Fluids,
Vol. 239,
Issue. ,
p.
105382.
Sahebjam, Rana
Kohan, Khashayar F.
and
Gaskin, Susan
2022.
The dynamics of an axisymmetric turbulent jet in ambient turbulence interpreted from the passive scalar field statistics.
Physics of Fluids,
Vol. 34,
Issue. 1,
Sofos, Filippos
Stavrogiannis, Christos
Exarchou-Kouveli, Kalliopi K.
Akabua, Daniel
Charilas, George
and
Karakasidis, Theodoros E.
2022.
Current Trends in Fluid Research in the Era of Artificial Intelligence: A Review.
Fluids,
Vol. 7,
Issue. 3,
p.
116.
Davydzenka, Tsimur
and
Tahmasebi, Pejman
2022.
High-resolution fluid–particle interactions: a machine learning approach.
Journal of Fluid Mechanics,
Vol. 938,
Issue. ,
Zhan, Qing-Liang
Bai, Chun-Jin
and
Ge, Yao-Jun
2022.
Deep learning representation of flow time history for complex flow field.
Acta Physica Sinica,
Vol. 71,
Issue. 22,
p.
224701.
Fang, L.
Bao, T.W.
Xu, W.Q.
Zhou, Z.D.
Du, J.L.
and
Jin, Y.
2022.
Data driven turbulence modeling in turbomachinery — An applicability study.
Computers & Fluids,
Vol. 238,
Issue. ,
p.
105354.
Qiu, Rundi
Huang, Renfang
Xiao, Yao
Wang, Jingzhu
Zhang, Zhen
Yue, Jieshun
Zeng, Zhong
and
Wang, Yiwei
2022.
Physics-informed neural networks for phase-field method in two-phase flow.
Physics of Fluids,
Vol. 34,
Issue. 5,
Li, Jinlu
Yu, Yanghai
and
Zhu, Weipeng
2022.
Ill-posedness for the Camassa-Holm and related equations in Besov spaces.
Journal of Differential Equations,
Vol. 306,
Issue. ,
p.
403.
Qiu, Chengcheng
Huang, Qiaogao
and
Pan, Guang
2022.
Prediction of Cavitation Performance over the Pump-Jet Propulsor Using Computational Fluid Dynamics and Hybrid Deep Learning Method.
Journal of Marine Science and Engineering,
Vol. 10,
Issue. 7,
p.
918.
Xiao, Li
Qi, Xueyuan
and
Li, Fengquan
2022.
Non-Uniform Dependence on Initial Data for the Rotation-Camassa–Holm Equation.
Journal of Mathematical Fluid Mechanics,
Vol. 24,
Issue. 4,
Qiu, Chengcheng
Huang, Qiaogao
Pan, Guang
and
He, Xing
2022.
Multi-path deep learning framework on discrete pressure points to predict velocity field of pump-jet propulsor.
Applied Ocean Research,
Vol. 123,
Issue. ,
p.
103173.
Kerestes, Jared N.
Marks, Christopher R.
Clark, John P.
Wolff, Mitch
Ni, Ron-Ho
and
Fletcher, Nathan
2023.
High-Lift High-Work LPT Blades and Separation: A Machine-Learning-Based Approach to Separation Identification.
Zhang, Zi-Qing
Li, Pei-Jing
Li, Qing-Kuo
Dong, Xu
Lu, Xin-Gen
and
Zhang, Yan-Feng
2023.
Dynamic Machine Learning Global Optimization Algorithm and Its Application to Aerodynamics.
Journal of Propulsion and Power,
Vol. 39,
Issue. 4,
p.
524.
2023.
A wall model learned from the periodic hill data and the law of the wall.
Physics of Fluids,
Vol. 35,
Issue. 5,
Ribeiro, Bernardo Luiz R.
and
Franck, Jennifer A.
2023.
Machine Learning to Classify Vortex Wakes of Energy Harvesting Oscillating Foils.
AIAA Journal,
Vol. 61,
Issue. 3,
p.
1281.
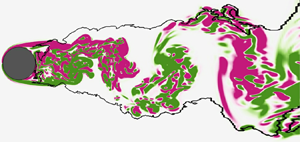
 $Re=100$ and 3900. Extreme gradient boosting (XGBoost) is utilized to train the detector, and after training, the detector is applied to identify the flow state at each point of the flow field. The trained detector is found robust in various tests, including the applications to the entire fields at successive snapshots and at a higher Reynolds number
$Re=100$ and 3900. Extreme gradient boosting (XGBoost) is utilized to train the detector, and after training, the detector is applied to identify the flow state at each point of the flow field. The trained detector is found robust in various tests, including the applications to the entire fields at successive snapshots and at a higher Reynolds number  $Re=5000$. The objectivity of the detector is verified by changing the input features and the flow region for choosing the turbulent training samples. Compared with the conventional methods, the proposed method based on machine learning shows its novelty in two aspects. First, no threshold value needs to be specified explicitly by the users. Second, machine learning can treat multiple input variables, which reflect different properties of turbulent flows, including the unsteadiness, vortex stretching and three-dimensionality. Owing to these advantages, XGBoost generates a detector that is more robust than those obtained from conventional methods.
$Re=5000$. The objectivity of the detector is verified by changing the input features and the flow region for choosing the turbulent training samples. Compared with the conventional methods, the proposed method based on machine learning shows its novelty in two aspects. First, no threshold value needs to be specified explicitly by the users. Second, machine learning can treat multiple input variables, which reflect different properties of turbulent flows, including the unsteadiness, vortex stretching and three-dimensionality. Owing to these advantages, XGBoost generates a detector that is more robust than those obtained from conventional methods.


