Crossref Citations
This article has been cited by the following publications. This list is generated based on data provided by
Crossref.
Barkley, D.
2019.
Taming turbulent fronts by bending pipes.
Journal of Fluid Mechanics,
Vol. 872,
Issue. ,
p.
1.
Wu, Renzhi
and
Qin, Lei
2019.
Numerical Study on Flow Characteristics and Energy Loss Mechanism in the 90° Circular Pipe Bend.
p.
403.
Lupi, Valerio
Canton, Jacopo
and
Schlatter, Philipp
2020.
Global stability analysis of a 90°-bend pipe flow.
International Journal of Heat and Fluid Flow,
Vol. 86,
Issue. ,
p.
108742.
Kumar, Anuj
2020.
Pressure-driven flows in helical pipes: bounds on flow rate and friction factor.
Journal of Fluid Mechanics,
Vol. 904,
Issue. ,
Canton, Jacopo
Rinaldi, Enrico
Örlü, Ramis
and
Schlatter, Philipp
2020.
Critical Point for Bifurcation Cascades and Featureless Turbulence.
Physical Review Letters,
Vol. 124,
Issue. 1,
Vavaliaris, Chris
Beneitez, Miguel
and
Henningson, Dan S.
2020.
Optimal perturbations and transition energy thresholds in boundary layer shear flows.
Physical Review Fluids,
Vol. 5,
Issue. 6,
Zhao, Yanlin
Yan, Yudong
Zhou, Xueyao
Yao, Jun
and
Wang, Chi-Hwa
2021.
Numerical investigation of electrostatic effect on particle behavior in a 90 degrees bend.
Advanced Powder Technology,
Vol. 32,
Issue. 3,
p.
810.
Yan, Yudong
Zhao, Yanlin
Yao, Jun
and
Wang, Chi-Hwa
2021.
Investigation of particle transport by a turbulent flow through a 90° bend pipe with electrostatic effects.
Powder Technology,
Vol. 394,
Issue. ,
p.
547.
Chen, Kaiwen
Xu, Duo
and
Song, Baofang
2022.
Propagation speed of turbulent fronts in pipe flow at high Reynolds numbers.
Journal of Fluid Mechanics,
Vol. 935,
Issue. ,
Nobis, Harrison
Schlatter, Philipp
Wadbro, Eddie
Berggren, Martin
and
Henningson, Dan S.
2022.
Topology optimization of unsteady flows using the spectral element method.
Computers & Fluids,
Vol. 239,
Issue. ,
p.
105387.
Liang, Chang-Hai
Sun, Ming-Bo
Huang, Yu-hui
Xiong, Da-Peng
Yu, Jiang-fei
Yang, Yi-Xin
Wang, Hong-Bo
Sun, Yong-chao
and
Ma, Guang-Wei
2022.
Mechanism of development of turbulent boundary layer in a curved circular pipe under supersonic conditions.
AIP Advances,
Vol. 12,
Issue. 3,
Frishman, Anna
and
Grafke, Tobias
2022.
Mechanism for turbulence proliferation in subcritical flows.
Proceedings of the Royal Society A: Mathematical, Physical and Engineering Sciences,
Vol. 478,
Issue. 2265,
Avila, Marc
Barkley, Dwight
and
Hof, Björn
2023.
Transition to Turbulence in Pipe Flow.
Annual Review of Fluid Mechanics,
Vol. 55,
Issue. 1,
p.
575.
Gomé, Sébastien
Tuckerman, Laurette S.
and
Barkley, Dwight
2023.
Patterns in transitional shear turbulence. Part 1. Energy transfer and mean-flow interaction.
Journal of Fluid Mechanics,
Vol. 964,
Issue. ,
Wu, Haoyang
and
Song, Baofang
2023.
Scaling and mechanism of the propagation speed of the upstream turbulent front in pipe flow.
Journal of Fluid Mechanics,
Vol. 977,
Issue. ,
Dunstan, Samuel D.
2023.
A direct numerical simulation display of the rotational frame preference of turbulence.
AIP Advances,
Vol. 13,
Issue. 4,
Nobis, Harrison
Schlatter, Philipp
Wadbro, Eddie
Berggren, Martin
and
Henningson, Dan S.
2023.
Modal laminar–turbulent transition delay by means of topology optimization of superhydrophobic surfaces.
Computer Methods in Applied Mechanics and Engineering,
Vol. 403,
Issue. ,
p.
115721.
Beneitez, Miguel
Duguet, Yohann
Schlatter, Philipp
and
Henningson, Dan S.
2023.
Instability of the optimal edge trajectory in the Blasius boundary layer.
Journal of Fluid Mechanics,
Vol. 971,
Issue. ,
Offermans, Nicolas
Massaro, Daniele
Peplinski, Adam
and
Schlatter, Philipp
2023.
Error-driven adaptive mesh refinement for unsteady turbulent flows in spectral-element simulations.
Computers & Fluids,
Vol. 251,
Issue. ,
p.
105736.
Gomé, Sébastien
Rivière, Aliénor
Tuckerman, Laurette S.
and
Barkley, Dwight
2024.
Phase Transition to Turbulence via Moving Fronts.
Physical Review Letters,
Vol. 132,
Issue. 26,
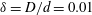 $\unicode[STIX]{x1D6FF}=D/d=0.01$ at several subcritical Reynolds numbers. Results show that the upstream overshoot of TKE production is at most one-and-a-half times the value in the core and that the average cross-flow fluctuations at the front are up to three times lower if compared to a straight pipe, while attaining similar values in the core. Localised turbulence can be sustained at smaller energies through a redistribution of turbulent fluctuations and vortical structures by the in-plane Dean motion of the mean flow. This asymmetry determines a strong localisation of TKE production near the outer bend, where linear and nonlinear mechanisms optimally amplify perturbations. We further observe a substantial reduction of the range of Reynolds numbers for long-lived intermittent turbulence, in agreement with experimental data from the literature. Moreover, no occurrence of nucleation of spots through splitting could be detected in the range of parameters considered. Based on the present results, we argue that this mechanism gradually becomes marginal as the curvature of the pipe increases and the transition scenario approaches a dynamical switch from subcritical to supercritical.
$\unicode[STIX]{x1D6FF}=D/d=0.01$ at several subcritical Reynolds numbers. Results show that the upstream overshoot of TKE production is at most one-and-a-half times the value in the core and that the average cross-flow fluctuations at the front are up to three times lower if compared to a straight pipe, while attaining similar values in the core. Localised turbulence can be sustained at smaller energies through a redistribution of turbulent fluctuations and vortical structures by the in-plane Dean motion of the mean flow. This asymmetry determines a strong localisation of TKE production near the outer bend, where linear and nonlinear mechanisms optimally amplify perturbations. We further observe a substantial reduction of the range of Reynolds numbers for long-lived intermittent turbulence, in agreement with experimental data from the literature. Moreover, no occurrence of nucleation of spots through splitting could be detected in the range of parameters considered. Based on the present results, we argue that this mechanism gradually becomes marginal as the curvature of the pipe increases and the transition scenario approaches a dynamical switch from subcritical to supercritical.