Hostname: page-component-78c5997874-fbnjt Total loading time: 0 Render date: 2024-11-10T09:08:52.397Z Has data issue: false hasContentIssue false
  • English
  • Français

Viscous control of shallow elastic fracture: peeling without precursors

Published online by Cambridge University Press:  08 April 2019

John R. Lister Open the ORCID record for John R. Lister [Opens in a new window] ,
Dominic J. Skinner  and
Timothy M. J. Large
John R. Lister*
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK
Dominic J. Skinner
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA
Timothy M. J. Large
Affiliation:
Department of Applied Mathematics and Theoretical Physics, University of Cambridge, Wilberforce Road, Cambridge CB3 0WA, UK Department of Mathematics, Massachusetts Institute of Technology, Cambridge, MA 02139-4307, USA
*
†Email address for correspondence: lister@damtp.cam.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider peeling of an elastic sheet away from an elastic substrate through propagation of a fluid-filled crack along the interface between the two. The peeling is driven by a bending moment applied to the sheet and is resisted by viscous flow towards the crack tip and by the toughness of any bonding between the sheet and the substrate. Travelling-wave solutions are determined using lubrication theory coupled to the full equations of elasticity and fracture. The propagation speed $v$ scales like 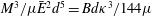$M^{3}/\unicode[STIX]{x1D707}\bar{E}^{2}d^{5}=Bd\unicode[STIX]{x1D705}^{3}/144\unicode[STIX]{x1D707}$, where 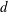$d$ is the sheet’s thickness, 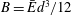$B=\bar{E}d^{3}/12$ its stiffness, 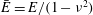$\bar{E}=E/(1-\unicode[STIX]{x1D708}^{2})$ its plane-strain modulus, 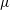$\unicode[STIX]{x1D707}$ the fluid viscosity, 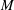$M$ the applied bending moment and 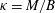$\unicode[STIX]{x1D705}=M/B$ the sheet’s curvature due to bending; and the prefactor depends on the dimensionless toughness. If the toughness is small then there is a region of dry shear failure ahead of the fluid-filled region. The expressions for the propagation speed have been used to derive new similarity solutions for the spread of an axisymmetric fluid-filled blister in a variety of regimes: constant-flux injection resisted by elastohydrodynamics in the tip leads to spread proportional to 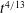$t^{4/13}$, 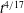$t^{4/17}$ and 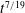$t^{7/19}$ for peeling-by-bending, gravitational spreading and peeling-by-pulling, respectively.

JFM classification

Low-Reynolds-number flows: Lubrication theory Geophysical and Geological Flows: Magma and lava flow
Type
JFM Papers
Information
Journal of Fluid Mechanics , Volume 868 , 10 June 2019 , pp. 119 - 140
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Ball, T. V. & Neufeld, J. A. 2018 Static and dynamic fluid-driven fracturing of adhered elastica. Phys. Rev. Fluids 7, 074101.Google Scholar
Bonn, D., Eggers, J., Indekeu, J., Meunier, J. & Rolley, E. 2009 Wetting and spreading. Rev. Mod. Phys. 81, 739–805.Google Scholar
Bunger, A. P. & Cruden, A. R. 2011 Modelling the growth of laccoliths and large mafic sills: role of magma body forces. J. Geophys. Res. 116, B02203; (and correction B08211).Google Scholar
Bunger, A. P. & Detournay, E. 2005 Asymptotic solution for a penny-shaped near-surface hydraulic fracture. Engng Fracture Mech. 72, 2468–2486.Google Scholar
Chopin, J., Vella, D. & Boudaoud, A. 2008 The liquid blister test. Proc. R. Soc. Lond. A 464, 2887–2906.Google Scholar
Cotterell, B. & Rice, J. R. 1980 Slightly curved or kinked cracks. Intl J. Fracture 16, 155–169.Google Scholar
Desroches, J., Detournay, E., Lenoach, B., Papanastasiou, P., Pearson, J. R. A., Thiercelin, M. & Cheng, A. 1994 The crack tip region in hydraulic fracturing. Proc. R. Soc. Lond. A 400, 39–48.Google Scholar
Detournay, E. 2016 Mechanics of hydraulic fractures. Annu. Rev. Fluid Mech. 48, 311–339.Google Scholar
Ducloué, L., Hazel, A. L., Thompson, A. B. & Juel, A. 2017 Reopening modes of a collapsed elasto-rigid channel. J. Fluid Mech. 819, 121–146.Google Scholar
Dyskin, A. V., Germanovich, L. N. & Ustinov, K. B. 2000 Asymptotic analysis of crack interaction with free boundary. Intl J. Solids Struct. 37, 857–886.Google Scholar
Flitton, J. C. & King, J. R. 2004 Moving-boundary and fixed-domain problems for a sixth-order thin-film equation. Eur. J. Appl. Maths 15, 713–754.Google Scholar
Garagash, D. I. & Detournay, E. 2000 The tip region of a fluid-driven fracture in an elastic medium. J. Appl. Mech. 67, 183–192.Google Scholar
Garagash, D. I. & Detournay, E. 2005 Plane-strain propagation of a fluid-driven fracture: small toughness solution. J. Appl. Mech. 72, 916–928.Google Scholar
Gomez, M., Moulton, D. E. & Vella, D. 2017 Passive control of viscous flow via elastic snap-through. Phys. Rev. Lett. 119, 144502.Google Scholar
Grotberg, J. B. & Jensen, O. E. 2004 Biofluid mechanics in flexible tubes. Annu. Rev. Fluid Mech. 36, 121–147.Google Scholar
Head, A. K. 1953 Edge dislocations in inhomogeneous media. Proc. Phys. Soc. Lond. B 66, 793–800.Google Scholar
Heil, M. & Hazel, A. 2011 Fluid-structure interaction in internal physiological flows. Annu. Rev. Fluid Mech. 43, 141–162.Google Scholar
Hervet, H. & de Gennes, P.-G. 1984 The dynamics of wetting: Precursor films in the wetting of ‘dry’ solids. C. R. Acad. Sci. II 299, 499–503.Google Scholar
Hewitt, I. J., Balmforth, N. J. & de Bruyn, J. R. 2015 Elastic-plated gravity currents. Eur. J. Appl. Maths 26, 1–31.Google Scholar
Hocking, L. M. 1983 The spreading of a thin drop by gravity and capillarity. Q. J. Mech. Appl. Maths 36, 55–69.Google Scholar
Hodges, S. R. & Jensen, O. E. 2002 Spreading and peeling dynamics in a model of cell adhesion. J. Fluid Mech. 460, 381–409.10.1017/S0022112002008340Google Scholar
Hosoi, A. E. & Mahadevan, L. 2004 Peeling, healing, and bursting in a lubricated elastic sheet. Phys. Rev. Lett. 93, 137802.Google Scholar
Jensen, H. M., Hutchinson, J. W. & Kim, K.-S. 1990 Decohesion of a cut prestressed film on a substrate. Intl J. Solids Struct. 26, 1099–1114.Google Scholar
Jensen, H. M. 1991 The blister test for interface toughness measurement. Engng Fracture Mech. 40, 475–486.Google Scholar
Jensen, O. E., Horsburgh, M. K., Halpern, D. & Gaver, D. P. 2002 The steady propagation of a bubble in a flexible-walled channel: asymptotic and computational models. Phys. Fluids. 14, 443–457.Google Scholar
Kanninen, M. F. & Popelar, C. H. 1985 Advanced Fracture Mechanics. Oxford.Google Scholar
Kavanagh, J. L., Rogers, B. D., Boutelier, D. & Cruden, A. R. 2017 Controls on sill and dyke-sill hybrid geometry and propagation in the crust: the role of fracture toughness. Tectonophysics 698, 109–120.Google Scholar
Leal, L. G. 1992 Laminar Flow and Convective Transport Processes. Butterworth-Heinemann.Google Scholar
Lister, J. R. 1990 Buoyancy-driven fluid fracture: the effects of material toughness and of low viscosity precursors. J. Fluid Mech. 210, 263–280.Google Scholar
Lister, J. R., Peng, G. G. & Neufeld, J. A. 2013 Viscous control of peeling an elastic sheet by bending and pulling. Phys. Rev. Lett. 111, 154501.Google Scholar
Leong, F. Y. & Chiam, K.-H. 2010 Adhesive dynamics of lubricated films. Phys. Rev. E 81, 041923.Google Scholar
McEwan, A. D. & Taylor, G. I. 1966 The peeling of a flexible strip attached by a viscous adhesive. J. Fluid Mech. 26, 1–15.Google Scholar
Meriaux, C. & Lister, J. R. 2002 Calculation of dyke trajectories from volcanic centres. J. Geophys. Res. 107, ETG 10-1–ETG 10-10.Google Scholar
Michaut, C. 2011 Dynamics of magmatic intrusions in the upper crust: theory and applications to laccoliths on Earth and the Moon. J. Geophys. Res. 116, B05205.Google Scholar
Peng, G. G.2017 Viscous flows under elastic sheets. PhD thesis, University of Cambridge.Google Scholar
Peng, G. G., Pihler-Puzović, J. A., Heil, M. & Lister, J. R. 2015 Displacement flows under elastic membranes. Part 2. Lubrication theory for two-phase flow. J. Fluid Mech. 784, 512–547.Google Scholar
Pihler-Puzović, D., Illien, P., Heil, M. & Juel, A. 2012 Suppression of complex fingerlike patterns at the interface between air and a viscous fluid by elastic membranes. Phys. Rev. Lett. 108, 074502.Google Scholar
Pihler-Puzović, J. A., Peng, G. G., Lister, J. R. & Heil, M. 2015 Displacement flows under elastic membrances. Part 1. Experiments and direct numerical simulations. J. Fluid Mech. 784, 487–511.Google Scholar
Pollard, D. D. & Johnson, A. M. 1973 Mechanics of growth of some laccolithic intrusions in the Henry Mountains, Utah, I: field observations, Gilbert’s model, physical properties and flow of the magma. Tectonophysics 18, 261–309.Google Scholar
Rice, J. R. 1968 Mathematical analysis in the mechanics of fracture. In Fracture, An Advanced Treatise (ed. Liebovitz, H.), vol. II, pp. 191–311. Academic Press.Google Scholar
Rogers, J. A., Someya, T. & Huang, Y. 2010 Materials and mechanics for stretchable electronics. Science 327, 1603–1607.Google Scholar
Spence, D. A. & Sharp, P. 1985 Self-similar solutions for elastohydrodynamic cavity flow. Proc. R. Soc. Lond. A 400, 289–313.Google Scholar
Suo, Z. & Hutchinson, J. W. 1990 Interface crack between two elastic layers. Intl J. Fracture 43, 1–18.Google Scholar
Thouless, M. D., Evans, A. G., Ashby, M. F. & Hutchinson, J. W. 1987 The edge cracking and spalling of brittle plates. Acta Metall. 35, 1333–1341.Google Scholar
Wang, Z.-Q. & Detournay, E. 2018 The tip region of a near-surface hydraulic fracture. J. Appl. Mech. 85, 041010.Google Scholar
Yang, F. & Li, J. C. M. 1997 Dislocation model of a subsurface crack. J. Appl. Phys. 82, 4816–4822.Google Scholar
Yuuki, R., Liu, J.-Q., Ohira, T. & Ono, T. 1994 Mixed mode fracture for an interface crack. Engng Fracture Mech. 47, 367–377.Google Scholar
Zhang, X., Detournay, E. & Jeffrey, R. G. 2002 Propagation of a penny-shaped hydraulic fracture parallel to the free-surface of an elastic half-space. Intl J. Fracture 115, 125–158.Google Scholar
Zhang, X., Jeffrey, R. G. & Detournay, E. 2005 Propagation of a hydraulic fracture parallel to a free surface. Intl J. Numer. Anal. Meth. Geomech. 29, 1317–1340.Google Scholar
Zlatin, A. H. & Khrapkov, A. A. 1986 A semi-infinite crack parallel to the boundary of the elastic half-plane. Dokl. Akad. Nauk SSSR 31, 1009–1010.Google Scholar