Article contents
Viscous effects on the fundamental solution to ship waves
Published online by Cambridge University Press: 01 October 2019
Abstract
The fundamental solution to steady ship waves accounting for viscous effects (the viscous-ship-wave Green function) is investigated within the framework of the weakly damped free-surface flow theory. An explicit expression of the viscous-ship-wave Green function is firstly derived, and an accurate and efficient technique is described to evaluate the Green function via decomposing the free-surface term into the local-flow component and wave component. To delve into the physical features of the viscous-ship-wave Green function, the asymptotic approximations in the far field due to Kelvin, Havelock and Peters are presented for the flow-field point located inside, at and outside the Kelvin wedge. In addition, uniform approximations to the wave component based on the Chester–Friedman–Ursell (CFU) approximation and the Kelvin–Havelock–Peters (KHP) approximation are carried out. Both numerical evaluation and asymptotic approximations show that the singular behaviour is eliminated and the divergent waves associated with large wavenumbers leading to rapid oscillations are severely damped when viscous effects are accounted for. In addition, viscous effects also alter the apparent wake angle associated with the wave pattern created by a high-speed translating source, and the apparent wake angle is dependent on both 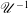 $\mathscr{U}^{-1}$ and
$\mathscr{U}^{-1}$ and 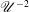 $\mathscr{U}^{-2}$, where
$\mathscr{U}^{-2}$, where  $\mathscr{U}$ is the translating speed of the source.
$\mathscr{U}$ is the translating speed of the source.
JFM classification
- Type
- JFM Papers
- Information
- Copyright
- © 2019 Cambridge University Press
References
- 13
- Cited by



