Hostname: page-component-cd9895bd7-hc48f Total loading time: 0 Render date: 2024-12-28T18:56:25.142Z Has data issue: false hasContentIssue false
  • English
  • Français

Volume displacement effects during bubble entrainment in a travelling vortex ring

Published online by Cambridge University Press:  13 March 2013

Andrew J. Cihonski ,
Justin R. Finn  and
Sourabh V. Apte
Andrew J. Cihonski
Affiliation:
School of Mechanical, Industrial and Manufacturing Engineering, Oregon State University, Corvallis, OR 97331, USA
Justin R. Finn
Affiliation:
School of Mechanical, Industrial and Manufacturing Engineering, Oregon State University, Corvallis, OR 97331, USA
Sourabh V. Apte*
Affiliation:
School of Mechanical, Industrial and Manufacturing Engineering, Oregon State University, Corvallis, OR 97331, USA
*
†Email address for correspondence: sva@engr.orst.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

When a few bubbles are entrained in a travelling vortex ring, it has been shown that, even at extremely low volume loadings, their presence can significantly affect the structure of the vortex core (Sridhar & Katz, J. Fluid Mech., vol. 397, 1999, pp. 171–202). A typical Euler–Lagrange point-particle model with two-way coupling for this dilute system, wherein the bubbles are assumed subgrid and momentum point sources are used to model their effect on the flow, is shown to be unable to capture accurately the experimental trends of bubble settling location, bubble escape and vortex distortion for a range of bubble parameters and vortex strengths. The bubbles experience significant amounts of drag, lift, added mass, pressure and gravity forces. However, these forces are in balance with each other as the bubbles reach a mean settling location away from the vortex core. The reaction force on the fluid due to the net summation of these forces alone is thus very small and is unable to affect the vortex core. By accounting for fluid volume displacement due to bubble motion, experimental trends on vortex distortion and bubble settling location are captured accurately. The fluid displacement effects are studied by computing various contributions to an effective volume displacement force and are found to be important even at low volume loadings. As the bubble size and hence bubble Reynolds number increase, the bubbles settle further away from the vortex centre and have strong potential for vortex distortion. The net volume displacement force depends on the radial pressure force, the radial settling location of the bubble, as well as the vortex Reynolds number. The resultant of the volume displacement force is found to be roughly at 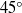$4{5}^{\circ } $ with the vortex travel direction, resulting in wakes directed towards the vortex centre. Finally, a simple modification to the standard point-particle two-way coupling approach is developed wherein the interphase reaction source terms are consistently altered to account for the fluid displacement effects and reactions due to bubble accelerations.

JFM classification

Drops and Bubbles: Bubble dynamics Multiphase and Particle-laden Flows: Multiphase flow Vortex Flows: Vortex interactions
Type
Papers
Information
Journal of Fluid Mechanics , Volume 721 , 25 April 2013 , pp. 225 - 267
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Apte, S. V., Mahesh, K. & Lundgren, T. 2008 Accounting for finite-size effects in simulations of disperse particle-laden flows. Intl J. Multiphase Flow 34 (3), 260–271.CrossRefGoogle Scholar
Apte, S. V., Mahesh, K., Moin, P. & Oefelein, J. C. 2003 Large-eddy simulation of swirling particle-laden flows in a coaxial-jet combustor. Intl J. Multiphase Flow 29 (8), 1311–1331.Google Scholar
Armenio, V. & Fiorotto, V. 2001 The importance of the forces acting on particles in turbulent flows. Phys. Fluids 13 (8), 2437–2440.Google Scholar
Balachandar, S. 2009 A scaling analysis for point particle approaches to turbulent multiphase flows. Intl J. Multiphase Flow 35 (9), 801–810.Google Scholar
Balachandar, S. & Eaton, J. K. 2010 Turbulent dispersed multiphase flow. Annu. Rev. Fluid Mech. 42 (1), 111–133.Google Scholar
Bluemink, J. J., Lohse, D., Prosperetti, A. & Van Wijngaarden, L. 2009 Drag and lift forces on particles in a rotating flow. J. Fluid Mech. 643, 1–31.Google Scholar
Ceccio, S. L. 2010 Friction drag reduction of external flows with bubble and gas injection. Annu. Rev. Fluid Mech. 42 (1), 183–203.Google Scholar
Darmana, D., Deen, N. G. & Kuipers, J. A. M. 2006 Parallelization of an Euler–Lagrange model using mixed domain decomposition and a mirror domain technique: application to dispersed gas–liquid two-phase flow. J. Comput. Phys. 220 (1), 216–248.CrossRefGoogle Scholar
Deng, R., Wang, C.-H. & Smith, K. 2006 Bubble behaviour in a Taylor vortex. Phys. Rev. E 73 (3), 036306.Google Scholar
Druzhinin, O. A. & Elghobashi, S. 1998 Direct numerical simulations of bubble-laden turbulent flows using the two-fluid formulation. Phys. Fluids 10 (3), 685–697.Google Scholar
Elghobashi, S. 1991 Particle–laden turbulent flows: direct simulation and closure models. Appl. Sci. Res. 48 (3–4), 301–314.CrossRefGoogle Scholar
Elghobashi, S. 1994 On predicting particle-laden turbulent flows. Appl. Sci. Res. 52 (4), 309–329.Google Scholar
Elghobashi, S. 2006 An updated classification map of particle-laden turbulent flows. In IUTAM Symposium on Computational Approaches to Multiphase Flow, vol. 81, pp. 3–10. Springer.CrossRefGoogle Scholar
Ferrante, A. & Elghobashi, S. 2005 Reynolds number effect on drag reduction in a microbubble-laden spatially developing turbulent boundary layer. J. Fluid Mech. 543 (1), 93–106.Google Scholar
Ferrante, A. & Elghobashi, S. 2007a On the accuracy of the two-fluid formulation in direct numerical simulation of bubble-laden turbulent boundary layers. Phys. Fluids 19 (4), 045105.Google Scholar
Ferrante, A. & Elghobashi, S. 2007b On the effects of microbubbles on Taylor–Green vortex flow. J. Fluid Mech. 572, 145–177.Google Scholar
Ferry, J. & Balachandar, S. 2001 A fast Eulerian method for disperse two-phase flow. Intl J. Multiphase Flow 27 (7), 1199–1226.Google Scholar
Fevrier, P., Simonin, O. & Squires, K. D. 2005 Partitioning of particle velocities in gas–solid turbulent flows into a continuous field and a spatially uncorrelated random distribution: theoretical formalism and numerical study. J. Fluid Mech. 533, 1–46.Google Scholar
Finn, J., Shams, E. & Apte, S. V. 2011 Modelling and simulation of multiple bubble entrainment and interactions with two-dimensional vortical flows. Phys. Fluids 23 (2), 023301.Google Scholar
Gatignol, R. 1983 Faxen formulae for a rigid particle in an unsteady non-uniform stokes flow. J. Méc. Théor. Appl. 1 (2), 143–160.Google Scholar
Gidaspow, D. 1994 Multiphase Flow and Fluidization: Continuum and Kinetic Theory Descriptions. Academic Press.Google Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31 (12), 3532.Google Scholar
Harper, J. 1972 The motion of bubbles and drops through liquids. In Advances in Applied Mechanics, vol. 12, pp. 59–129. Elsevier.Google Scholar
Higuera, F. J. 2004 Axisymmetric inviscid interaction of a bubble and a vortex ring. Phys. Fluids 16, 1156–1159.Google Scholar
van der Hoef, M. A., van Sint Annaland, M., Deen, N. G. & Kuipers, J. A. M. 2008 Numerical simulation of dense gas–solid fluidized beds: a multiscale modelling strategy. Annu. Rev. Fluid Mech. 40 (1), 47–70.CrossRefGoogle Scholar
Hsiao, C.-T. & Chahine, G. 2004 Prediction of tip vortex cavitation inception using coupled spherical and nonspherical bubble models and Navier–Stokes computations. J. Mar. Sci. Technol. 8 (3), 99–108.Google Scholar
Jackson, R. 1997 Locally averaged equations of motion for a mixture of identical spherical particles and a Newtonian fluid. Chem. Engng Sci. 52 (15), 2457–2469.Google Scholar
James, S. & Madnia, C. K. 1996 Direct numerical simulation of a laminar vortex ring. Phys. Fluids 8 (9), 2400–2414.Google Scholar
Joseph, D., Lundgren, T., Jackson, R. & Saville, D. 1990 Ensemble averaged and mixture theory equations for incompressible fluid particle suspensions. Intl J. Multiphase Flow 16 (1), 35–42.Google Scholar
Kuipers, J. A. M., van Duin, K. J., van Beckum, F. P. H. & van Swaaij, W. P. M. 1993 Computer simulation of the hydrodynamics of a two-dimensional gas-fluidized bed. Comput. Chem. Engng 17 (8), 839–858.CrossRefGoogle Scholar
Lain, S. & Garcia, J. A. 2006 Study of four-way coupling on turbulent particle-laden jet flows. Chem. Engng Sci. 61 (20), 6775–6785.CrossRefGoogle Scholar
Li, Y., McLaughlin, J. B., Kontomaris, K. & Portela, L. 2001 Numerical simulation of particle-laden turbulent channel flow. Phys. Fluids 13 (10), 2957–2967.Google Scholar
Lohse, D. & Prosperetti, A. 2003 Controlling bubbles. J. Phys.: Condens. Matter 15 (1), S415–S420.Google Scholar
Magnaudet, J. & Eames, I. 2000 The motion of high-Reynolds-number bubbles in inhomogeneous flows. Annu. Rev. Fluid Mech. 32 (1), 659–708.Google Scholar
Maxey, M. R. & Riley, J. J. 1987 Gravitational settling of aerosol particles in homogeneous turbulence and random flow fields. J. Fluid Mech. 174 (1), 441–465.Google Scholar
Maxey, M. R. 1983 Equation of motion for a small rigid sphere in a non-uniform flow. Phys. Fluids 26 (4), 883–889.Google Scholar
Mazzitelli, I. & Lohse, D. 2009 Evolution of energy in flow driven by rising bubbles. Phys. Rev. E 79 (6), 066317.Google Scholar
Mazzitelli, I. M., Lohse, D. & Toschi, F. 2003 The effect of microbubbles on developed turbulence. Phys. Fluids 15 (1), L5.CrossRefGoogle Scholar
Merle, A., Legendre, D. & Magnaudet, J. 2005 Forces on a high-Reynolds-number spherical bubble in a turbulent flow. J. Fluid Mech. 532, 53–62.Google Scholar
Mittal, R., Dong, H., Bozkurttas, M., Najjar, F. M., Vargas, A. & Von Loebbecke, A. 2008 A versatile sharp interface immersed boundary method for incompressible flows with complex boundaries. J. Comput. Phys. 227 (10), 4825–4852.Google Scholar
Mohseni, K., Ran, H. & Colonius, T. 2001 Numerical experiments on vortex ring formation. J. Fluid Mech. 430, 267–282.Google Scholar
Moin, P. & Apte, S. V. 2006 Large-eddy simulation of realistic gas turbine combustors. AIAA J. v44 698, 698–708.Google Scholar
Ormières, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83 (1), 80–83.Google Scholar
Oweis, G. F., van der Hout, I. E., Iyer, C., Tryggvason, G. & Ceccio, S. L. 2005 Capture and inception of bubbles near line vortices. Phys. Fluids 17 (2), 022105.Google Scholar
Rastello, M., Marié, J.-L., Grosjean, N. & Lance, M. 2009 Drag and lift forces on interface-contaminated bubbles spinning in a rotating flow. J. Fluid Mech. 624 (1), 159–178.Google Scholar
Rastello, M., Marié, J.-L. & Lance, M. 2011 Drag and lift forces on clean spherical and ellipsoidal bubbles in a solid-body rotating flow. J. Fluid Mech. 682, 434–459.Google Scholar
Reade, W. C. & Collins, L. R. 2000 Effect of preferential concentration on turbulent collision rates. Phys. Fluids 12, 2530.Google Scholar
Rouson, D. W. I. & Eaton, J. K. 2001 On the preferential concentration of solid particles in turbulent channel flow. J. Fluid Mech. 428 (1), 149–169.Google Scholar
Schiller, L. & Naumann, A. 1935 A drag coefficient correlation. Z. Verein. Deutsch. Ing. 77, 318–320.Google Scholar
Segura, J. C., Eaton, J. K. & Oefelein, J. C. 2004 Predictive capabilities of particle-laden large-eddy simulation. Report No. TSD-156, Department of Mechanical Engineering, Stanford University.Google Scholar
Shams, E. & Apte, S. V. 2010 Prediction of small-scale cavitation in a high speed flow over an open cavity using large-eddy simulation. Trans. ASME: J. Fluids Engng 132, 111301.Google Scholar
Shams, E., Finn, J. & Apte, S. V. 2011 A numerical scheme for Euler–Lagrange simulation of bubbly flows in complex systems. Intl J. Numer. Meth. Fluids 67 (12), 1865–1898.Google Scholar
Sokolichin, A., Eigenberger, G., Lapin, A. & Lubert, A. 1997 Dynamic numerical simulation of gas–liquid two-phase flows: Euler/Euler versus Euler/Lagrange. Chem. Engng Sci. 52 (4), 611–626.Google Scholar
Sommerfeld, M., Ando, A. & Wennerberg, D. 1992 Swirling, particle-laden flows through a pipe expansion. J. Fluids Engng 114 (4), 648–656.Google Scholar
Sommerfeld, M. & Qiu, H. H. 1993 Characterization of particle-laden, confined swirling flows by phase-Doppler anemometry and numerical calculation. Intl J. Multiphase Flow 19 (6), 1093–1127.CrossRefGoogle Scholar
Squires, K. D. & Eaton, J. K. 1991 Preferential concentration of particles by turbulence. Phys. Fluids A: Fluid Dyn. 3 (5), 1169.Google Scholar
Sridhar, G. & Katz, J. 1995 Drag and lift forces on microscopic bubbles entrained by a vortex. Phys. Fluids 7 (2), 389.Google Scholar
Sridhar, G. & Katz, J. 1999 Effect of entrained bubbles on the structure of vortex rings. J. Fluid Mech. 397, 171–202.Google Scholar
Tomboulides, A. G. & Orszag, S. A. 2000 Numerical investigation of transitional and weak turbulent flow past a sphere. J. Fluid Mech. 416 (1), 45–73.Google Scholar
Van Nierop, E. A., Luther, S., Bluemink, J. J., Magnaudet, J., Prosperetti, A. & Lohse, D. 2007 Drag and lift forces on bubbles in a rotating flow. J. Fluid Mech. 571, 439–454.Google Scholar
Vreman, A. W. 2007 Turbulence characteristics of particle-laden pipe flow. J. Fluid Mech. 584, 235–279.Google Scholar
Wang, Q. & Squires, K. D. 1996 Large eddy simulation of particle-laden turbulent channel flow. Phys. Fluids 8, 1207–1223.Google Scholar
Xu, J., Maxey, M. R. & Karniadakis, G. E. 2002 Numerical simulation of turbulent drag reduction using micro-bubbles. J. Fluid Mech. 468 (1), 271–281.Google Scholar
Yamamoto, Y., Potthoff, M., Tanaka, T., Kajishima, T. & Tsuji, Y. 2001 Large-eddy simulation of turbulent gas particle flow in a vertical channel: effect of considering inter-particle collisions. J. Fluid Mech. 442, 303–334.Google Scholar
Zhang, D. Z. & Prosperetti, A. 1997 Momentum and energy equations for disperse two-phase flows and their closure for dilute suspensions. Intl J. Multiphase Flow 23 (3), 425–453.Google Scholar