Article contents
Vortex generation due to internal solitary wave propagation past a sidewall constriction
Published online by Cambridge University Press: 03 March 2021
Abstract
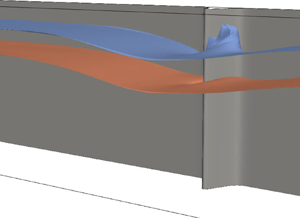
Internal solitary waves in the coastal ocean propagate in a complex environment, with variations in the background currents and stratification and with topography along both the bottom (e.g. sills) and sides (e.g. headlands). We present direct numerical simulations of internal solitary wave propagation past an isolated sidewall constriction on laboratory scales. We find that the wave-induced currents generate separation regions which develop into vortices above and below the wave-deformed pycnocline. These vortices yield horizontal tracer exchange between the near-wall region and channel interior and vertical transport sufficient to lift pycnocline fluid near to the surface. Quantitatively, the height of the vertical transport was found to be proportional to the square of the vertical vorticity. Increases in the wave amplitude and the aspect ratio of the constriction (height to width) led to stronger vortices, greater lateral and vertical transport and enhanced density overturning. We compare and contrast these findings with the literature on isolated bottom topography, focusing on the inherently three-dimensional nature (vorticity aligned perpendicular to isopycnals) of the instability in the sidewall case as opposed to typical instabilities caused by internal solitary waves.
Information
- Type
- JFM Papers
- Information
- Copyright
- © The Author(s), 2021. Published by Cambridge University Press
References
REFERENCES
- 9
- Cited by


