Hostname: page-component-78c5997874-v9fdk Total loading time: 0 Render date: 2024-11-10T06:41:17.341Z Has data issue: false hasContentIssue false
  • English
  • Français

Vortex-induced vibrations of an elastically mounted sphere with three degrees of freedom at Re = 300: hysteresis and vortex shedding modes

Published online by Cambridge University Press:  03 October 2011

Suresh Behara ,
Iman Borazjani  and
Fotis Sotiropoulos
Suresh Behara
Affiliation:
Saint Anthony Falls Laboratory, University of Minnesota, 2 Third Avenue SE, Minneapolis, MN 55414, USA
Iman Borazjani
Affiliation:
Saint Anthony Falls Laboratory, University of Minnesota, 2 Third Avenue SE, Minneapolis, MN 55414, USA
Fotis Sotiropoulos*
Affiliation:
Saint Anthony Falls Laboratory, University of Minnesota, 2 Third Avenue SE, Minneapolis, MN 55414, USA
*
†Email address for correspondence: fotis@umn.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Fluid–structure interaction (FSI) simulations are carried out to investigate vortex-induced vibrations of a sphere, mounted on elastic supports in all three spatial directions. The reduced velocity (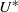) is systematically varied in the range 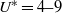, while the Reynolds number and reduced mass are held fixed at 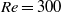and 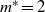, respectively. In the lock-in regime, two distinct branches are observed in the response curve, each corresponding to a distinct type of vortex shedding, namely, hairpin and spiral vortices. While shedding of hairpin vortices has been observed in several previous investigations of stationary and vibrating spheres, the shedding of intertwined, longitudinal spiral vortices in the wake of a vibrating sphere is reported herein for the first time. When the wake is in the hairpin shedding mode, the sphere moves along a linear path in the transverse plane, while when spiral vortices are shed, the sphere vibrates along a circular orbit. In the spiral mode branch, the simulations reveal hysteresis in the response amplitude at the beginning of the lock-in regime. Lower-amplitude vibrations are found as the sphere sheds hairpin vortices for increasing 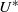up until the beginning of the synchronization regime. On the other hand, higher-amplitude oscillations persist for the spiral mode as is decreased from the point of the start of the synchronization. The hairpin mode is found to be unstable for the value of reduced velocity where the spiral and hairpin solution branches merge together. When this point is approached along the hairpin solution branch, the sphere naturally transitions from shedding hairpin vortices and moving along a linear path to shedding spiral vortices and moving along a circular path in the transverse plane. The spiral mode was not observed in the work of Horowitz & Williamson (J. Fluid Mech., vol. 651, 2010, pp. 251–294), who studied experimentally the vibration modes of a freely rising or falling sphere and only reported zigzag vibrations. Our results suggest that this apparent discrepancy between experiments and simulations should be attributed to the fact that, for the range of governing parameters considered in the simulations, the elastic supports act to suppress streamwise vibrations, thus subjecting the sphere to a nearly axisymmetric elasticity constraint and enabling it to vibrate transversely along a circular path.

JFM classification

Aerodynamics: Flow-structure interactions Vortex Flows: Vortex shedding
Type
Papers
Information
Journal of Fluid Mechanics , Volume 686 , 10 November 2011 , pp. 426 - 450
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Present address: 337 Jarvis Hall, University at Buffalo SUNY, Buffalo, NY 14260, USA.

References

1. Allen, D. W. & Henning, D. L. 2003 Vortex-induced vibration current tank tests of two equal diameter cylinders in tandem. J. Fluids Struct. 17 (6), 767–781.CrossRefGoogle Scholar
2. Assi, G. R. S., Meneghini, J. R., Aranha, J. A. P., Bearman, P. W. & Casaprima, E. 2006 Experimental investigation of flow-induced vibration interference between two circular cylinders. J. Fluids Struct. 22 (6), 819–827.CrossRefGoogle Scholar
3. Bearman, P. W. 1984 Vortex shedding from oscillating bluff bodies. Annu. Rev. Fluid Mech. 16, 195–222.CrossRefGoogle Scholar
4. Bishop, R. E. D. & Hassan, A. Y. 1964 The lift and drag forces on a circular cylinder oscillating in a flowing fluid. J. Fluid Mech. 277, 51–75.Google Scholar
5. Borazjani, I. 2008 Numerical simulations of fluid–structure interaction problems in biological flows. PhD thesis, University of Minnesota, Twin Cities.Google Scholar
6. Borazjani, I., Ge, L. & Sotiropoulos, F. 2008 Curvilinear immersed boundary method for simulating fluid structure interaction with complex three-dimensional rigid bodies. J. Comput. Phys. 227 (16), 7587–7620.CrossRefGoogle Scholar
7. Borazjani, I. & Sotiropoulos, F. 2008 Numerical investigation of the hydrodynamics of carangiform swimming in the transitional and inertial flow regimes. J. Expl. Biol. 211, 1541–1558.CrossRefGoogle ScholarPubMed
8. Borazjani, I. & Sotiropoulos, F. 2009 Vortex-induced vibrations of two cylinders to tandem arrangement in the proximity-wake interface region. J. Fluid Mech. 621 (16), 321–364.CrossRefGoogle Scholar
9. Brika, D. & Lanville, A. 1993 Vortex induced vibrations of long flexible circular cylinder. J. Fluid Mech. 250, 481–508.CrossRefGoogle Scholar
10. Brucker, C. 1999 Structure and dynamics of the wake of bubbles and its relevance for bubble interaction. Phys. Fluids 11 (7), 1781–1796.CrossRefGoogle Scholar
11. Dasi, L. P., Ge, L., Simon, H. A., Sotiropoulos, F. & Yoganathan, A. P. 2007 Vorticity dynamics of a bileaflet mechanical valve in an axisymmetric aorta. Phys. Fluids 19, 067105.CrossRefGoogle Scholar
12. Feng, C. C. 1968 The measurement of vortex-induced effects in flow past a stationary and oscillating circular cylinder and D-section cylinders. Master’s thesis, University of British Columbia.Google Scholar
13. Ge, L. & Sotiropoulos, F. 2007 A numerical method for solving the three-dimensional unsteady incompressible Navier–Stokes equations in curvilinear domains with complex immersed boundaries. J. Comput. Phys. 225, 1782–1809.CrossRefGoogle Scholar
14. Gilmanov, A. & Sotiropoulos, F. 2005 A hybrid Cartesian/immersed boundary method for simulating flows with three-dimensional, geometrically complex, moving bodies. J. Comput. Phys. 207 (2), 457.CrossRefGoogle Scholar
15. Gilmanov, A., Sotiropoulos, F. & Balaras, E. 2003 A general reconstruction algorithm for simulating flows with complex 3D immersed boundaries on Cartesian grids. J. Comput. Phys. 191, 660–669.CrossRefGoogle Scholar
16. Govardhan, R. & Williamson, C. H. K. 1997 Vortex-induced motions of a tethered sphere. J. Wind Engng Ind. Aerodyn. 69–71, 375–385.CrossRefGoogle Scholar
17. Govardhan, R. N. & Williamson, C. H. K. 2005 Vortex-induced vibrations of a sphere. J. Fluid Mech. 531, 11–47.CrossRefGoogle Scholar
18. Horowitz, M. & Williamson, C. H. K. 2010 The effect of Reynolds number on the dynamics and wakes of freely rising and falling spheres. J. Fluid Mech. 651, 251–294.CrossRefGoogle Scholar
19. Hunt, J. C. R., Wray, A. A. & Moin, P. 1988 Eddies, streams, and convergence zones in turbulent flows. Proceedings of the 1988 Summer Program on Studying Turbulence Using Numerical Simulation Databases (SEE N89-24538 18-34), vol. 2, 193–208.Google Scholar
20. Jauvtis, N., Govardhan, R. & Williamson, C. H. K. 2001 Multiple modes of vortex-induced vibration of a sphere. J. Fluids Struct. 15, 555–563.CrossRefGoogle Scholar
21. Jauvtis, N. & Williamson, C. H. K. 2004 The effect of two degrees of freedom on vortex-induced vibration at low mass and damping. J. Fluid Mech. 509, 23–62.CrossRefGoogle Scholar
22. Johnson, T. A. & Patel, V. C. 1999 Flow past a sphere up to a Reynolds number of 300. J. Fluid Mech. 378, 19–70.CrossRefGoogle Scholar
23. Khalak, A. & Williamson, C. H. K. 1996 Dynamics of a hydroelastic cylinder with very low mass and damping. J. Fluids Struct. 10, 455–472.CrossRefGoogle Scholar
24. Khalak, A. & Williamson, C. H. K. 1997 Fluid forces and dynamics of a hydroelastic structure with very low mass and damping. J. Fluids Struct. 11, 973–982.CrossRefGoogle Scholar
25. Khalak, A. & Williamson, C. H. K. 1999 Motions, forces and mode transitions in vortex-induced vibrations at low mass-damping. J. Fluids Struct. 13, 813–851.CrossRefGoogle Scholar
26. Mittal, R. 1999a Planar symmetry in the unsteady wake of sphere. AIAA J. 37 (3), 388–390.CrossRefGoogle Scholar
27. Mittal, R. 1999b Fourier–Chebyshev spectral collocation method for simulating flow past spheres and spheroids. Intl J. Numer. Meth. Fluids 30, 921–937.3.0.CO;2-3>CrossRefGoogle Scholar
28. Mittal, S. & Kumar, V. 1999 Finite element study of vortex-induced cross-flow and in-line oscillations of a circular cylinder at low Reynolds numbers. Intl J. Numer. Meth. Fluids 31, 1087–1120.3.0.CO;2-C>CrossRefGoogle Scholar
29. Moe, G. & Wu, Z. J. 1990 The lift force on a cylinder vibrating in a current. J. Offshore Mech. Arctic Engng 112, 297–303.CrossRefGoogle Scholar
30. Mougin, G. & Magnaudet, J. 2002 Path instability of a rising bubble. Phys. Rev. Lett. 88 (1) 014502-1.Google ScholarPubMed
31. Ormieres, D. & Provansal, M. 1999 Transition to turbulence in the wake of a sphere. Phys. Rev. Lett. 83, 80–83.CrossRefGoogle Scholar
32. Prasanth, T. K., Behara, S., Singh, S. P., Kumar, R. & Mittal, S. 2006 Effect of blockage on vortex-induced vibrations at low Reynolds numbers. J. Fluids Struct. 22, 865–876.CrossRefGoogle Scholar
33. Prasanth, T. K. & Mittal, S. 2008 Vortex-induced vibrations of a circular cylinder at low Reynolds numbers. J. Fluid Mech. 594, 463–491.CrossRefGoogle Scholar
34. Prasanth, T. K. & Mittal, S. 2009 Vortex-induced vibrations of two circular cylinders at low Reynolds number. J. Fluids Struct. 25, 731–741.CrossRefGoogle Scholar
35. Provansal, M., Leweke, T., Schouveiler, L. & Guebert, N. 2003 3D oscillations and vortex-induced vibrations of a tethered sphere in a flow parallel to the thread. Proceedings of PSFVIP-4, Chamonix, France, 3–5 June.Google Scholar
36. Provansal, M., Schouveiler, L. & Leweke, T. 1999 From the double vortex street behind a cylinder to the wake of a sphere. Eur. J. Mech. (B/Fluids) 23, 6580.Google Scholar
37. Roos, F. W. & Willmarth, W. W. 1971 Some experimental results on sphere and disk drag. AIAA J. 9, 285–291.CrossRefGoogle Scholar
38. Sakamoto, H. & Haniu, H. 1990 A study on vortex shedding from spheres in a uniform flow. Trans. ASME 112, 386–392.Google Scholar
39. Sarpkaya, T. 2004 A critical review of the intrinsic nature of vortex induced vibrations. J. Fluids Struct. 19 (4), 389–447.CrossRefGoogle Scholar
40. Singh, S. P. & Mittal, S. 2005 Vortex-induced oscillations at low Reynolds numbers: hysteresis and vortex shedding modes. J. Fluids Struct. 20, 1085–1104.CrossRefGoogle Scholar
41. Tobak, M. & Peake, D. J. 1982 Topology of three-dimensional separated flows. Annu. Rev. Fluid Mech. 14, 61–85.CrossRefGoogle Scholar
42. Tomboulides, A. G. 1993 Direct and large-eddy simulation of wake flows: flow past a sphere. PhD thesis, Princeton University.CrossRefGoogle Scholar
43. Tomboulides, A. G., Orszag, S. A. & Karniadakis, G. E. 1993 Direct and large-eddy simulations of axisymmetric wakes. AIAA Paper 93-0546.CrossRefGoogle Scholar
44. Williamson, C. H. K. & Govardhan, R. 1997 Dynamics and forcing of a tethered sphere in a fluid flow. J. Fluids Struct. 11, 293–303.CrossRefGoogle Scholar
45. Williamson, C. H. K. & Govardhan, R. 2004 Vortex induced vibration. Annu. Rev. Fluid Mech. 36, 413–455.CrossRefGoogle Scholar
46. Williamson, C. H. K. & Roshko, A. 1988 Vortex formation in the wake of an oscillating cylinder. J. Fluids Struct. 2 (4), 355–381.CrossRefGoogle Scholar
47. Zdravkovich, M. M. 1985 Flow induced oscillations of two interfering circular cylinders. J. Sound Vib. 101 (4), 511–521.CrossRefGoogle Scholar