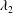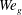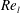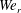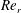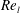1 Introduction
When a liquid jet discharges into a gaseous medium, it becomes unstable and breaks into droplets due to instabilities. In combustion and jet propulsion applications, the common purpose of breaking a liquid stream into spray is to increase the liquid surface area so that heat and mass and combustion transfer rate can be increased. Even though the liquid jet breakup has been studied theoretically, experimentally and numerically for more than half a century, the liquid surface deformation mechanisms and their causes are still not satisfactorily understood, nor categorized in different operating regimes. In this study, a spatially developing round liquid jet with slower outer gas flow is studied numerically. The main objective here is to examine the interaction of the vortices near the gas–liquid interface, and to see how those interactions vary with gas-to-liquid velocity ratio, and their consequent effects on the surface deformation and instabilities. In this respect, the causes of the axial vorticity generation are analysed to find the main source of the three-dimensional (3-D) instabilities of the initially axisymmetric jets. To understand these causes and their variation with velocity ratio, the acting forces on the liquid surface are analysed separately in the three coordinate directions.
The Kelvin–Helmholtz (KH) instability at the gas–liquid interface is the primary cause of surface deformation and wave formation, which leads to primary breakup. Jarrahbashi & Sirignano (Reference Jarrahbashi and Sirignano2014) showed that the KH instability promotes the growth of azimuthal vorticity waves forming coherent vortices which later deform and become asymmetric as the vortex rings move downstream. In this general definition, the KH instability occurs at the interface of two parallel flows with different velocities. The viscosity contrast considered in Yih instability (Yih Reference Yih1967), and the surface tension effects considered by Funada & Joseph (Reference Funada and Joseph2001) are both factored in the KH instability term used here, along the already considered density stratification.
Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000) in their review of the liquid-jet atomization in a high speed coaxial gas stream, categorized the regimes of liquid-jet breakup and showed the effects of gas-to-liquid momentum ratio in those regimes. However, they did not relate those regimes to the dynamics of vortices generated prior to atomization. Shinjo & Umemura (Reference Shinjo and Umemura2010) briefly touched upon the axial and radial vortices generated in the round liquid-jet atomization process (without coaxial flow) and showed that the orientation of vortices determines the orientation of ligaments during the primary breakup; however, they mainly focused on the vortices near the jet tip and claimed that the primary breakup was mainly affected by the vortices that are advected upstream from the jet tip, without detailing the vortex interactions. More recently, Jarrahbashi & Sirignano (Reference Jarrahbashi and Sirignano2014) – hereafter cited as JS – and Jarrahbashi et al. (Reference Jarrahbashi, Sirignano, Popov and Hussain2016) studied the details of vortex dynamics in a temporal study of a round liquid-jet segment, and showed that the vortices can also form far upstream of the jet cap. They related the vortex interactions to the surface deformation, lobe formation and perforation. Later, Zandian, Sirignano & Hussain (Reference Zandian, Sirignano and Hussain2017) – hereafter cited as ZSH1 – and Zandian, Sirignano & Hussain (Reference Zandian, Sirignano and Hussain2018) – hereafter cited as ZSH2 – extended the vortex dynamics analysis to the atomization of planar liquid sheets and identified three main atomization regimes with different characteristic length and time scales and unique breakup mechanisms based only on the liquid Reynolds number (
![]() $Re_{l}$
) and gas Weber number (
$Re_{l}$
) and gas Weber number (
![]() $We_{g}$
). They showed that one can explain each breakup mechanism by following the vortex interactions near the gas–liquid interface. Ling et al. (Reference Ling, Fuster, Zaleski and Tryggvason2017) also observed the hairpin vortex structures emphasized by ZSH2 at the surface of a spatial liquid jet, but did not address the details of those vortex interactions. These hairpin structures transport momentum and provide a means of producing turbulent kinetic energy. Although controversial, hairpins can autogenerate to form packets that populate the boundary layer, the dynamics of which are discussed in detail by Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000) and Adrian (Reference Adrian2007).
$We_{g}$
). They showed that one can explain each breakup mechanism by following the vortex interactions near the gas–liquid interface. Ling et al. (Reference Ling, Fuster, Zaleski and Tryggvason2017) also observed the hairpin vortex structures emphasized by ZSH2 at the surface of a spatial liquid jet, but did not address the details of those vortex interactions. These hairpin structures transport momentum and provide a means of producing turbulent kinetic energy. Although controversial, hairpins can autogenerate to form packets that populate the boundary layer, the dynamics of which are discussed in detail by Adrian, Meinhart & Tomkins (Reference Adrian, Meinhart and Tomkins2000) and Adrian (Reference Adrian2007).
ZSH1 and ZSH2 performed a temporal numerical study on a planar liquid-sheet segment with imposed periodic conditions, and showed similar mechanisms in the breakup of both planar and round liquid jets. Here, we perform an analysis similar to ZSH2, but with inclusion of a slow coaxial outer gas flow, for a spatially developing round jet. This study shows the validity of the prior temporal studies and their relevance to a real atomization application. The formation of vortex structures both on the jet stem and in the cap region are more closely followed and quantified. In this analysis, the effects of gas–liquid velocity ratio (and relative gas–liquid velocity) on the vortex dynamics and surface deformation are also delineated.
1.1 Objectives
Our goal is to study the vortex dynamics and its influence on the liquid surface dynamics in order to understand the breakup mechanisms at different operating conditions. To this end, the
![]() $\unicode[STIX]{x1D706}_{2}$
criterion introduced by Jeong & Hussain (Reference Jeong and Hussain1995) and detailed in § 2.4 is used to define a vortex. The main objective is to understand the effects of relative gas–liquid velocity on the axial vortex generation and azimuthal surface deformation. For this purpose, the balance between the forces acting on the interface are analysed in detail. The outcome of this analysis helps us identify the atomization domains for coaxial liquid jets following the decomposition that was achieved by the temporal studies with no outer gas flow (ZSH1).
$\unicode[STIX]{x1D706}_{2}$
criterion introduced by Jeong & Hussain (Reference Jeong and Hussain1995) and detailed in § 2.4 is used to define a vortex. The main objective is to understand the effects of relative gas–liquid velocity on the axial vortex generation and azimuthal surface deformation. For this purpose, the balance between the forces acting on the interface are analysed in detail. The outcome of this analysis helps us identify the atomization domains for coaxial liquid jets following the decomposition that was achieved by the temporal studies with no outer gas flow (ZSH1).
2 Numerical modelling
2.1 Governing equations
The three-dimensional Navier–Stokes (NS) equations with volume-of-fluid (VoF) interface capturing method yield computational results for the liquid jet which captures the gas–liquid interface deformations in space and time.
The incompressible continuity and NS equations, including the viscous diffusion and surface tension forces and neglecting the gravitational force are as follows:
where
![]() $\boldsymbol{u}$
is the velocity vector, and
$\boldsymbol{u}$
is the velocity vector, and
![]() $p$
,
$p$
,
![]() $\unicode[STIX]{x1D70C}$
and
$\unicode[STIX]{x1D70C}$
and
![]() $\unicode[STIX]{x1D707}$
are the pressure, density and dynamic viscosity of the fluid, respectively. The rate of deformation tensor,
$\unicode[STIX]{x1D707}$
are the pressure, density and dynamic viscosity of the fluid, respectively. The rate of deformation tensor,
![]() $\unicode[STIX]{x1D63F}$
, is given by
$\unicode[STIX]{x1D63F}$
, is given by
The last term in (2.2) is the surface tension force per unit volume
![]() $\boldsymbol{F}=-\unicode[STIX]{x1D70E}\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FF}(d)\boldsymbol{n}$
; where
$\boldsymbol{F}=-\unicode[STIX]{x1D70E}\unicode[STIX]{x1D705}\unicode[STIX]{x1D6FF}(d)\boldsymbol{n}$
; where
![]() $\unicode[STIX]{x1D70E}$
is the surface tension coefficient,
$\unicode[STIX]{x1D70E}$
is the surface tension coefficient,
![]() $\unicode[STIX]{x1D705}$
is the surface curvature,
$\unicode[STIX]{x1D705}$
is the surface curvature,
![]() $\unicode[STIX]{x1D6FF}(d)$
is the Dirac delta function,
$\unicode[STIX]{x1D6FF}(d)$
is the Dirac delta function,
![]() $d$
is the distance from the interface and
$d$
is the distance from the interface and
![]() $\boldsymbol{n}$
is the unit vector normal to the gas–liquid interface.
$\boldsymbol{n}$
is the unit vector normal to the gas–liquid interface.
The VoF method developed by Hirt & Nichols (Reference Hirt and Nichols1981) captures the gas–liquid interface and describes the evolution of the two-phase flow in time and space. In this method, the liquid volume fraction
![]() $f$
is advected by the velocity field. The following transport equation is solved to account for the transportation of
$f$
is advected by the velocity field. The following transport equation is solved to account for the transportation of
![]() $f$
(Hirt & Nichols Reference Hirt and Nichols1981).
$f$
(Hirt & Nichols Reference Hirt and Nichols1981).
where the VoF-variable
![]() $f$
represents the liquid volume fraction at each cell as follows
$f$
represents the liquid volume fraction at each cell as follows
 $$\begin{eqnarray}f(t)=\left\{\begin{array}{@{}ll@{}}0,\quad & \mathit{outside~of~liquid~phase},\\ 0<f<1,\quad & \mathit{at~the~interface},\\ 1,\quad & \mathit{inside~the~liquid~phase}.\end{array}\right.\end{eqnarray}$$
$$\begin{eqnarray}f(t)=\left\{\begin{array}{@{}ll@{}}0,\quad & \mathit{outside~of~liquid~phase},\\ 0<f<1,\quad & \mathit{at~the~interface},\\ 1,\quad & \mathit{inside~the~liquid~phase}.\end{array}\right.\end{eqnarray}$$
Since fluid properties are required at every time step in order to solve the NS equations, the density and viscosity change continuously based on the value of
![]() $f$
.
$f$
.
2.2 Flow configuration
The 3-D computational domain forms a rectangular box, shown in figure 1. The domain initially contains quiescent gas. The liquid jet of diameter
![]() $D=200~\unicode[STIX]{x03BC}\text{m}$
is injected from the left boundary starting at time
$D=200~\unicode[STIX]{x03BC}\text{m}$
is injected from the left boundary starting at time
![]() $t_{0}$
with uniform velocity
$t_{0}$
with uniform velocity
![]() $U_{l}$
. The domain size is
$U_{l}$
. The domain size is
![]() $15D\times 6D\times 6D$
, in the
$15D\times 6D\times 6D$
, in the
![]() $x$
(axial),
$x$
(axial),
![]() $y$
and
$y$
and
![]() $z$
(radial) directions, respectively. The coaxial gas stream over the rest of the inlet boundary has a constant velocity
$z$
(radial) directions, respectively. The coaxial gas stream over the rest of the inlet boundary has a constant velocity
![]() $U_{g}$
. The Lagrangian derivative of all velocity components are set to zero at the four side boundaries. The right boundary is the outlet, where the normal gradient of all velocity components (except for the axial velocity) and the volume fraction are set to zero. The axial velocity is normalized by the ratio of inlet to outlet mass fluxes (
$U_{g}$
. The Lagrangian derivative of all velocity components are set to zero at the four side boundaries. The right boundary is the outlet, where the normal gradient of all velocity components (except for the axial velocity) and the volume fraction are set to zero. The axial velocity is normalized by the ratio of inlet to outlet mass fluxes (
![]() ${\dot{m}}_{out}/{\dot{m}}_{in}$
) to conserve the mass inside the system.
${\dot{m}}_{out}/{\dot{m}}_{in}$
) to conserve the mass inside the system.

Figure 1. The 3-D computational domain.
To mimic the turbulence introduced by the liquid flow inside the nozzle (upstream of the computational box), the inlet velocity of the liquid jet is perturbed in time with a very small amplitude,
The amplitude coefficient
![]() $\unicode[STIX]{x1D6FC}$
is chosen to be 0.2 %, and the mean liquid-jet velocity
$\unicode[STIX]{x1D6FC}$
is chosen to be 0.2 %, and the mean liquid-jet velocity
![]() $U_{l}$
is taken to be
$U_{l}$
is taken to be
![]() $50~\text{m}~\text{s}^{-1}$
(
$50~\text{m}~\text{s}^{-1}$
(
![]() $80~\text{m}~\text{s}^{-1}$
in one case). Five modes are considered in the temporal velocity profile which would correspond to spatial wavelengths in the range
$80~\text{m}~\text{s}^{-1}$
in one case). Five modes are considered in the temporal velocity profile which would correspond to spatial wavelengths in the range
![]() $D/4=50~\unicode[STIX]{x03BC}\text{m}$
to
$D/4=50~\unicode[STIX]{x03BC}\text{m}$
to
![]() $3D/4=150~\unicode[STIX]{x03BC}\text{m}$
. This covers the range of instability wavelengths that are reported in the literature for the given dimensionless parameters (Jarrahbashi & Sirignano Reference Jarrahbashi and Sirignano2014; Yang & Turan Reference Yang and Turan2017). The temporal variation of the inlet liquid velocity is plotted in figure 2. The given modes let the flow field determine the dominant wavelengths that grow the fastest and naturally dissipate and damp the other perturbations.
$3D/4=150~\unicode[STIX]{x03BC}\text{m}$
. This covers the range of instability wavelengths that are reported in the literature for the given dimensionless parameters (Jarrahbashi & Sirignano Reference Jarrahbashi and Sirignano2014; Yang & Turan Reference Yang and Turan2017). The temporal variation of the inlet liquid velocity is plotted in figure 2. The given modes let the flow field determine the dominant wavelengths that grow the fastest and naturally dissipate and damp the other perturbations.

Figure 2. Temporal profile of the inlet velocity.
The most important dimensionless groups in this study are the liquid Reynolds number (
![]() $Re_{l}$
), the gas Weber number (
$Re_{l}$
), the gas Weber number (
![]() $We_{g}$
), the gas-to-liquid density ratio (
$We_{g}$
), the gas-to-liquid density ratio (
![]() $\hat{\unicode[STIX]{x1D70C}}$
), viscosity ratio (
$\hat{\unicode[STIX]{x1D70C}}$
), viscosity ratio (
![]() $\hat{\unicode[STIX]{x1D707}}$
) and velocity ratio (
$\hat{\unicode[STIX]{x1D707}}$
) and velocity ratio (
![]() $\hat{U}$
), defined as
$\hat{U}$
), defined as
The jet radius
![]() $R$
is the characteristic length of this problem. For the characteristic velocity, the liquid-jet velocity
$R$
is the characteristic length of this problem. For the characteristic velocity, the liquid-jet velocity
![]() $U_{l}$
is mainly used in the literature. However, our results indicate that the more relevant characteristic velocity is the relative velocity of the liquid with respect to the gas; i.e.
$U_{l}$
is mainly used in the literature. However, our results indicate that the more relevant characteristic velocity is the relative velocity of the liquid with respect to the gas; i.e.
![]() $U_{r}=U_{l}-U_{g}$
. The subscripts
$U_{r}=U_{l}-U_{g}$
. The subscripts
![]() $l$
and
$l$
and
![]() $g$
refer to the liquid and gas, respectively. In this regard the relative Reynolds and Weber numbers are defined as
$g$
refer to the liquid and gas, respectively. In this regard the relative Reynolds and Weber numbers are defined as
![]() $Re_{r}=\unicode[STIX]{x1D70C}_{l}U_{r}R/\unicode[STIX]{x1D707}_{l}$
and
$Re_{r}=\unicode[STIX]{x1D70C}_{l}U_{r}R/\unicode[STIX]{x1D707}_{l}$
and
![]() $We_{r}=\unicode[STIX]{x1D70C}_{g}U_{r}^{2}R/\unicode[STIX]{x1D70E}$
.
$We_{r}=\unicode[STIX]{x1D70C}_{g}U_{r}^{2}R/\unicode[STIX]{x1D70E}$
.
Our main focus is on the effects of
![]() $\hat{U}$
on the atomization process. Three gas velocities –
$\hat{U}$
on the atomization process. Three gas velocities –
![]() $U_{g}=5,10$
and
$U_{g}=5,10$
and
![]() $25~\text{m}~\text{s}^{-1}$
– are considered, which result in
$25~\text{m}~\text{s}^{-1}$
– are considered, which result in
![]() $\hat{U}=0.1,0.2$
and
$\hat{U}=0.1,0.2$
and
![]() $0.5$
, respectively. The liquid and gas properties, and hence
$0.5$
, respectively. The liquid and gas properties, and hence
![]() $Re_{l}$
,
$Re_{l}$
,
![]() $We_{g}$
,
$We_{g}$
,
![]() $\hat{\unicode[STIX]{x1D70C}}$
and
$\hat{\unicode[STIX]{x1D70C}}$
and
![]() $\hat{\unicode[STIX]{x1D707}}$
are kept the same for all three cases. In order to better evaluate the relative importance of velocity ratio and velocity difference in the results, a fourth case is also considered with
$\hat{\unicode[STIX]{x1D707}}$
are kept the same for all three cases. In order to better evaluate the relative importance of velocity ratio and velocity difference in the results, a fourth case is also considered with
![]() $U_{l}=80~\text{m}~\text{s}^{-1}$
and
$U_{l}=80~\text{m}~\text{s}^{-1}$
and
![]() $U_{g}=40~\text{m}~\text{s}^{-1}$
. This case has a similar
$U_{g}=40~\text{m}~\text{s}^{-1}$
. This case has a similar
![]() $\hat{U}=0.5$
to case 3, and a similar
$\hat{U}=0.5$
to case 3, and a similar
![]() $U_{r}=40~\text{m}~\text{s}^{-1}$
to case 2. The goal is to understand which one of those cases does case 4 resemble more closely. The values of all the dimensionless parameters for the four cases are listed in table 1. The liquid is kerosene with
$U_{r}=40~\text{m}~\text{s}^{-1}$
to case 2. The goal is to understand which one of those cases does case 4 resemble more closely. The values of all the dimensionless parameters for the four cases are listed in table 1. The liquid is kerosene with
![]() $\unicode[STIX]{x1D70C}_{l}=800~\text{kg}~\text{m}^{-3}$
,
$\unicode[STIX]{x1D70C}_{l}=800~\text{kg}~\text{m}^{-3}$
,
![]() $\unicode[STIX]{x1D707}_{l}=2\times 10^{-3}~\text{Pa}~\text{s}$
and
$\unicode[STIX]{x1D707}_{l}=2\times 10^{-3}~\text{Pa}~\text{s}$
and
![]() $\unicode[STIX]{x1D70E}=0.024~\text{N}~\text{m}^{-1}$
.
$\unicode[STIX]{x1D70E}=0.024~\text{N}~\text{m}^{-1}$
.
Table 1. The dimensionless parameter values for the cases studied.

2.3 Numerical methods
Direct numerical simulation is done using an unsteady 3-D finite-volume solver for the NS equations for the round incompressible liquid jet and its coaxial gas stream. A uniform staggered grid is used with a mesh size of
![]() $\unicode[STIX]{x1D6E5}=2~\unicode[STIX]{x03BC}\text{m}$
and a time step of
$\unicode[STIX]{x1D6E5}=2~\unicode[STIX]{x03BC}\text{m}$
and a time step of
![]() $\unicode[STIX]{x0394}t=5~\text{ns}$
. A third-order accurate QUICK scheme is used for spatial discretization of the fluxes and the Crank–Nicolson scheme is used for time marching. The continuity and momentum equations are coupled through the SIMPLE algorithm.
$\unicode[STIX]{x0394}t=5~\text{ns}$
. A third-order accurate QUICK scheme is used for spatial discretization of the fluxes and the Crank–Nicolson scheme is used for time marching. The continuity and momentum equations are coupled through the SIMPLE algorithm.
The fully conservative momentum convection and volume fraction transport, the momentum diffusion and the surface tension are treated implicitly. To ensure a sharp interface of all flow discontinuities and to suppress numerical dissipation of the liquid phase, the interface is reconstructed at each time step by the piecewise linear interface calculation (known as PLIC) method of Rider & Kothe (Reference Rider and Kothe1998). The normal direction of the interface is found by considering the volume fractions in a neighbourhood of the cell considered, where
![]() $f$
changes most rapidly. A least-square method introduced by Puckett et al. (Reference Puckett, Almgren, Bell, Marcus and Rider1997) is used for normal reconstruction, where the interface is approximated by a straight plane in the cell block. Once interface reconstruction has been performed, direction-split geometrical fluxes are computed for VoF advection (Popinet Reference Popinet2009). This advection scheme preserves sharp interfaces and is close to second-order accurate for practical atomization applications. We use the paraboloid fitting technique of Popinet (Reference Popinet2009) to compute an accurate estimate of the curvature from the discrete volume fraction values.
$f$
changes most rapidly. A least-square method introduced by Puckett et al. (Reference Puckett, Almgren, Bell, Marcus and Rider1997) is used for normal reconstruction, where the interface is approximated by a straight plane in the cell block. Once interface reconstruction has been performed, direction-split geometrical fluxes are computed for VoF advection (Popinet Reference Popinet2009). This advection scheme preserves sharp interfaces and is close to second-order accurate for practical atomization applications. We use the paraboloid fitting technique of Popinet (Reference Popinet2009) to compute an accurate estimate of the curvature from the discrete volume fraction values.
The grid resolution and the computational domain size were chosen with great care to ensure grid independent and domain-size independent results. The effects of mesh size on the atomization process was analysed extensively in the prior studies (ZSH1; ZSH2; JS), and it was shown that the considered grid does not affect the size of various liquid structures (e.g. bridges, ligaments and droplets) and their formation time and location. The vorticity profile (as an important quantity of interest) was also checked for different mesh sizes, similar to the analysis performed by ZSH2. The given mesh size was found to be fine enough to predict and resolve the vortex structures correctly.
2.4 Data analysis
Our goal is to study the vortex dynamics as well as the liquid surface dynamics in order to relate the surface deformation and cascade of liquid structures to the velocity ratio. To this end,
![]() $\unicode[STIX]{x1D706}_{2}$
isosurfaces are identified and analysed in time. Here, we briefly review the definition of the
$\unicode[STIX]{x1D706}_{2}$
isosurfaces are identified and analysed in time. Here, we briefly review the definition of the
![]() $\unicode[STIX]{x1D706}_{2}$
method (Jeong & Hussain Reference Jeong and Hussain1995).
$\unicode[STIX]{x1D706}_{2}$
method (Jeong & Hussain Reference Jeong and Hussain1995).
An objective definition of a vortex should permit the use of vortex dynamics concepts to identify coherent structures (CS), to explain the formation and evolutionary dynamics of CS, and to explore the role of CS in turbulence phenomena. Jeong & Hussain (Reference Jeong and Hussain1995) define a vortex core as a connected region with two negative eigenvalues of
![]() $\unicode[STIX]{x1D64E}^{2}+\unicode[STIX]{x1D734}^{2}$
; where,
$\unicode[STIX]{x1D64E}^{2}+\unicode[STIX]{x1D734}^{2}$
; where,
![]() $\unicode[STIX]{x1D64E}$
and
$\unicode[STIX]{x1D64E}$
and
![]() $\unicode[STIX]{x1D734}$
are the symmetric and anti-symmetric components of
$\unicode[STIX]{x1D734}$
are the symmetric and anti-symmetric components of
![]() $\unicode[STIX]{x1D735}u$
; i.e.
$\unicode[STIX]{x1D735}u$
; i.e.
![]() $\unicode[STIX]{x1D61A}_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})$
and
$\unicode[STIX]{x1D61A}_{ij}=\frac{1}{2}(u_{i,j}+u_{j,i})$
and
![]() $\unicode[STIX]{x1D6FA}_{ij}=\frac{1}{2}(u_{i,j}-u_{j,i})$
. If
$\unicode[STIX]{x1D6FA}_{ij}=\frac{1}{2}(u_{i,j}-u_{j,i})$
. If
![]() $\unicode[STIX]{x1D706}_{1}$
,
$\unicode[STIX]{x1D706}_{1}$
,
![]() $\unicode[STIX]{x1D706}_{2}$
and
$\unicode[STIX]{x1D706}_{2}$
and
![]() $\unicode[STIX]{x1D706}_{3}$
, are the eigenvalues such that
$\unicode[STIX]{x1D706}_{3}$
, are the eigenvalues such that
![]() $\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \unicode[STIX]{x1D706}_{3}$
, this definition is equivalent to the requirement that
$\unicode[STIX]{x1D706}_{1}\geqslant \unicode[STIX]{x1D706}_{2}\geqslant \unicode[STIX]{x1D706}_{3}$
, this definition is equivalent to the requirement that
![]() $\unicode[STIX]{x1D706}_{2}<0$
within the vortex core, since
$\unicode[STIX]{x1D706}_{2}<0$
within the vortex core, since
![]() $\unicode[STIX]{x1D706}_{3}$
is always negative because the sum of the normal viscous stresses is zero. This definition has been proved to meet the requirements for existence of a vortex core in different flow conditions (Jeong & Hussain Reference Jeong and Hussain1995), while the vortex identification by the Q-definition (Kolář Reference Kolář2007) may be incorrect when vortices are subjected to a strong external strain (Jeong & Hussain Reference Jeong and Hussain1995), as in our study. It should be noted that Yao & Hussain (Reference Yao and Hussain2018) have recently developed a new vortex definition which should prove effective for studying vortical structures in multiphase flows.
$\unicode[STIX]{x1D706}_{3}$
is always negative because the sum of the normal viscous stresses is zero. This definition has been proved to meet the requirements for existence of a vortex core in different flow conditions (Jeong & Hussain Reference Jeong and Hussain1995), while the vortex identification by the Q-definition (Kolář Reference Kolář2007) may be incorrect when vortices are subjected to a strong external strain (Jeong & Hussain Reference Jeong and Hussain1995), as in our study. It should be noted that Yao & Hussain (Reference Yao and Hussain2018) have recently developed a new vortex definition which should prove effective for studying vortical structures in multiphase flows.
3 Results and discussion
3.1 Identification of surface deformations
Two types of surface perturbations are distinguished when a liquid jet is injected into a gaseous medium – shown schematically in figure 3(a) and in the 3-D simulation result in figure 3(b). The detached droplets and ligaments have been removed in figure 3(b) to better display the surface waves on the liquid-jet core. The first region is right behind the jet start-up cap, to the right of the broken red line in figure 3(a), and is called the behind-the-cap region (BCR). In this region, the gas phase velocity is faster than the liquid jet and thus, the relative local velocity of the gas stream points downstream. The gas shear creates negative azimuthal vorticity, negative
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
, near the interface, which generates KH vortices and consequently downstream-facing KH waves in figure 4. The vortices in the BCR are inside the recirculation zone behind the cap – the region inside the box in figure 4 – and the surface deformations are directly related to the dynamics of the growing cap and can be explained by the vortex interactions in that region. Shinjo & Umemura (Reference Shinjo and Umemura2010) briefly discussed this region in their 3-D simulation of a round liquid-jet with no coaxial flow, and while describing that the vortex dynamics in this region are very complex, they showed that the vortex orientation determines the orientation of the ligaments that are broken from the cap. The surface pattern is not periodic in the BCR. Even though this region is not the main focus of our study, kinematics of the cap and the BCR waves are analysed later in this section.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
, near the interface, which generates KH vortices and consequently downstream-facing KH waves in figure 4. The vortices in the BCR are inside the recirculation zone behind the cap – the region inside the box in figure 4 – and the surface deformations are directly related to the dynamics of the growing cap and can be explained by the vortex interactions in that region. Shinjo & Umemura (Reference Shinjo and Umemura2010) briefly discussed this region in their 3-D simulation of a round liquid-jet with no coaxial flow, and while describing that the vortex dynamics in this region are very complex, they showed that the vortex orientation determines the orientation of the ligaments that are broken from the cap. The surface pattern is not periodic in the BCR. Even though this region is not the main focus of our study, kinematics of the cap and the BCR waves are analysed later in this section.

Figure 3. Schematic of vortex regions and wave transmission paths (a). Liquid-jet surface showing different instability types and their propagation directions in case 1 (b).

Figure 4. Azimuthal vorticity (
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) contours showing vortices near the interface – case 1.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) contours showing vortices near the interface – case 1.
The second type of surface deformation occurs farther upstream of the cap, to the left of the broken red line in figure 3(a), and we call it the upstream region (UR). In the UR, the liquid-phase velocity is faster than the gas, and the relative gas–liquid velocity points upstream. The gas shear creates positive
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
which creates upstream-facing KH waves. Shinjo & Umemura (Reference Shinjo and Umemura2011) mention that Tollmien–Schlichting (TS) waves develop within the gas phase while the interface remains smooth and the liquid phase serves as a solid surface for the gas phase. The importance of the TS waves relative to KH waves remains to be fully determined. Yecko, Zaleski & Fullana (Reference Yecko, Zaleski and Fullana2002) perform a linear stability analysis for the coupled gas and liquid viscous flow with interfacial tension and find three unstable modes: a TS mode for the gas viscous layer, a TS mode for the liquid viscous layer, and an interfacial (i.e. KH) mode. The dominant mode and its wavelength can change depending on viscosity ratio and density ratio. For air and water, they show significant dominance of the interfacial mode with the liquid TS mode substantially stronger than the gas TS mode. Figure 5 shows the streamwise velocity distribution at four radial distances from the axis – the black line at
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
which creates upstream-facing KH waves. Shinjo & Umemura (Reference Shinjo and Umemura2011) mention that Tollmien–Schlichting (TS) waves develop within the gas phase while the interface remains smooth and the liquid phase serves as a solid surface for the gas phase. The importance of the TS waves relative to KH waves remains to be fully determined. Yecko, Zaleski & Fullana (Reference Yecko, Zaleski and Fullana2002) perform a linear stability analysis for the coupled gas and liquid viscous flow with interfacial tension and find three unstable modes: a TS mode for the gas viscous layer, a TS mode for the liquid viscous layer, and an interfacial (i.e. KH) mode. The dominant mode and its wavelength can change depending on viscosity ratio and density ratio. For air and water, they show significant dominance of the interfacial mode with the liquid TS mode substantially stronger than the gas TS mode. Figure 5 shows the streamwise velocity distribution at four radial distances from the axis – the black line at
![]() $z/D=0.45$
is very close to the interface and inside the liquid boundary layer, the blue and green lines (
$z/D=0.45$
is very close to the interface and inside the liquid boundary layer, the blue and green lines (
![]() $z/D=0.525$
and
$z/D=0.525$
and
![]() $z/D=0.55$
) are very close to the interface and inside the gas boundary layer, while the red line is much farther in the gas phase. The location of each line is denoted in the magnified view of the interface in the centre panel. Consistent with Yecko & Zaleski (Reference Yecko and Zaleski2005), these results show that the interfacial instabilities are dominant over the TS mode and the perturbations are more pronounced in the liquid than in the gas. This leads to our preference for the KH theory in explaining the UR waves.
$z/D=0.55$
) are very close to the interface and inside the gas boundary layer, while the red line is much farther in the gas phase. The location of each line is denoted in the magnified view of the interface in the centre panel. Consistent with Yecko & Zaleski (Reference Yecko and Zaleski2005), these results show that the interfacial instabilities are dominant over the TS mode and the perturbations are more pronounced in the liquid than in the gas. This leads to our preference for the KH theory in explaining the UR waves.

Figure 5. Streamwise velocity distribution at different radial distances in the UR near the nozzle exit; case 1, at
![]() $t^{\ast }=11.25$
.
$t^{\ast }=11.25$
.
It is noteworthy that, pulsating the velocity of the inlet liquid triggers the interface perturbations, which amplifies the lean towards the KH instabilities in our study. If the wavy surface causes an adverse pressure gradient locally, the domain of instability can be expected to reach higher wavenumbers than would be obtained for the flat surface studied by Shinjo & Umemura (Reference Shinjo and Umemura2011). Kundu & Cohen (Reference Kundu and Cohen1990) indicate that the margin for instability for higher
![]() $Re$
occurs with the product of wavenumber and displacement thickness being nearly constant. Since we expect the thickness to vary inversely with the square root of relative velocity, it follows that wavelength is inversely proportional to the square root of relative velocity at the margin. Later, we will see this behaviour in our results.
$Re$
occurs with the product of wavenumber and displacement thickness being nearly constant. Since we expect the thickness to vary inversely with the square root of relative velocity, it follows that wavelength is inversely proportional to the square root of relative velocity at the margin. Later, we will see this behaviour in our results.
Shinjo & Umemura (Reference Shinjo and Umemura2010) claim that the UR dynamics are highly affected by the BCR dynamics since the shed vortices and the broken droplets are transmitted upstream from the jet cap. However, we note that the vortices shed from the cap rim mainly affect the droplet propagation in the UR, are far from the interface and have minor interactions with the UR KH waves (see figure 4). Thus, the surface dynamics in the UR can be studied separately from the BCR. These UR vortices are more effective on the surface deformation and atomization since they mainly control the cascade process on a larger portion of the jet stem compared to the smaller region behind the cap where the cap has influence. This supports the value of the temporal analyses with periodic boundary conditions, such as those by JS, Jarrahbashi et al. (Reference Jarrahbashi, Sirignano, Popov and Hussain2016), ZSH1, and ZSH2.
A large indentation occurs between the UR and BCR regions – caused by the radially inward gas flow due to the cap vortex (figures 3 and 4). The gas stream then branches into two opposite streams, one flowing downstream and the other upstream in the frame of reference of the jet. At the stagnation point, pressure is higher and the liquid is pressed inward. Similar indentation was also observed in Shinjo & Umemura (Reference Shinjo and Umemura2010, figure 15a), although not emphasized by them. We draw the line between the two regions at the centre of this indentation. Shinjo & Umemura (Reference Shinjo and Umemura2010), however, did not identify an exact criterion for the borderline between these two regions, and their BCR and UR regions overlapped at some places and also stretched beyond our proposed borderline.

Figure 6. Average KH wavelength for different velocity ratios for a constant
![]() $U_{l}$
.
$U_{l}$
.
3.2 Kinematics of the surface instabilities
Figure 6 compares the average wavelength of the axial surface instabilities for different
![]() $\hat{U}$
values. The temporally perturbed inlet velocity would produce surface perturbations in the range
$\hat{U}$
values. The temporally perturbed inlet velocity would produce surface perturbations in the range
![]() $50{-}150~\unicode[STIX]{x03BC}\text{m}$
. By increasing
$50{-}150~\unicode[STIX]{x03BC}\text{m}$
. By increasing
![]() $\hat{U}$
from 0.1 to 0.5, the average KH wavelength,
$\hat{U}$
from 0.1 to 0.5, the average KH wavelength,
![]() $\unicode[STIX]{x1D706}_{KH}$
, increases from 80 (
$\unicode[STIX]{x1D706}_{KH}$
, increases from 80 (
![]() $\unicode[STIX]{x1D706}_{KH}/D=0.4$
) to
$\unicode[STIX]{x1D706}_{KH}/D=0.4$
) to
![]() $100~\unicode[STIX]{x03BC}\text{m}$
(
$100~\unicode[STIX]{x03BC}\text{m}$
(
![]() $\unicode[STIX]{x1D706}_{KH}/D=0.5$
). In the given range of
$\unicode[STIX]{x1D706}_{KH}/D=0.5$
). In the given range of
![]() $\hat{U}$
, wavelengths vary from
$\hat{U}$
, wavelengths vary from
![]() $70~\unicode[STIX]{x03BC}\text{m}$
to
$70~\unicode[STIX]{x03BC}\text{m}$
to
![]() $130~\unicode[STIX]{x03BC}\text{m}$
. Matas, Delon & Cartellier (Reference Matas, Delon and Cartellier2018) showed that in shear flows confinement could lead to resonance, and enhancement of wavelengths of the order of the confining length (expected to be the jet radius,
$130~\unicode[STIX]{x03BC}\text{m}$
. Matas, Delon & Cartellier (Reference Matas, Delon and Cartellier2018) showed that in shear flows confinement could lead to resonance, and enhancement of wavelengths of the order of the confining length (expected to be the jet radius,
![]() $=100~\unicode[STIX]{x03BC}\text{m}$
, here) depending on boundary conditions. Their work, however, applies to much larger gas–liquid velocity ratios.
$=100~\unicode[STIX]{x03BC}\text{m}$
, here) depending on boundary conditions. Their work, however, applies to much larger gas–liquid velocity ratios.
Shinjo & Umemura (Reference Shinjo and Umemura2011) in their linear two-dimensional analysis of steady gas–liquid boundary layers found that the streamwise (KH) instability wavelength is proportional to the inverse of the square root of liquid velocity, i.e.
![]() $\unicode[STIX]{x1D706}_{KH}\propto 1/\sqrt{U_{l}}$
. Since their analysis was for
$\unicode[STIX]{x1D706}_{KH}\propto 1/\sqrt{U_{l}}$
. Since their analysis was for
![]() $U_{g}=0$
, we assume that this expression can be modified for coaxial jets by using
$U_{g}=0$
, we assume that this expression can be modified for coaxial jets by using
![]() $U_{r}$
instead of
$U_{r}$
instead of
![]() $U_{l}$
. With this modification, the streamwise wavelength for coaxial jets becomes
$U_{l}$
. With this modification, the streamwise wavelength for coaxial jets becomes
where
![]() $C$
is a constant. Our simulation results are compared to the expression obtained in (3.1) with
$C$
is a constant. Our simulation results are compared to the expression obtained in (3.1) with
![]() $C\approx 2.62$
, in figure 6. A good agreement within 7 % is achieved between our results and theory (Shinjo & Umemura Reference Shinjo and Umemura2011). The discrepancies may be due to the neglected effects of surface tension and 3-D curvature of the liquid jet in their linear analysis. Unlike Shinjo & Umemura (Reference Shinjo and Umemura2011), our results indicate that the effect of relative velocity on the axial wavelength becomes less significant as
$C\approx 2.62$
, in figure 6. A good agreement within 7 % is achieved between our results and theory (Shinjo & Umemura Reference Shinjo and Umemura2011). The discrepancies may be due to the neglected effects of surface tension and 3-D curvature of the liquid jet in their linear analysis. Unlike Shinjo & Umemura (Reference Shinjo and Umemura2011), our results indicate that the effect of relative velocity on the axial wavelength becomes less significant as
![]() $\hat{U}$
increases because, with the decrease of
$\hat{U}$
increases because, with the decrease of
![]() $U_{r}$
, the inertial effects diminish and the surface deformation is mainly governed by the viscous and surface tension forces, which are less reliant on the gas velocity than inertia. Therefore, the wavelengths would not diverge as
$U_{r}$
, the inertial effects diminish and the surface deformation is mainly governed by the viscous and surface tension forces, which are less reliant on the gas velocity than inertia. Therefore, the wavelengths would not diverge as
![]() $U_{g}\rightarrow U_{l}$
as proposed by (3.1) from the linear analysis of Shinjo & Umemura (Reference Shinjo and Umemura2011).
$U_{g}\rightarrow U_{l}$
as proposed by (3.1) from the linear analysis of Shinjo & Umemura (Reference Shinjo and Umemura2011).
Figure 6 clearly indicates that the most relevant characteristic velocity in coaxial flows is the relative velocity between the liquid and gas streams, i.e.
![]() $U_{r}$
. Thus, since
$U_{r}$
. Thus, since
![]() $Re_{l}$
is the same for all three cases, the pertinent Reynolds number should also be based on
$Re_{l}$
is the same for all three cases, the pertinent Reynolds number should also be based on
![]() $U_{r}$
and not the injection velocity which is widely used in the literature. As
$U_{r}$
and not the injection velocity which is widely used in the literature. As
![]() $\hat{U}$
decreases, hence
$\hat{U}$
decreases, hence
![]() $Re_{r}$
increases,
$Re_{r}$
increases,
![]() $\unicode[STIX]{x1D706}_{KH}$
decreases, as intuitively expected.
$\unicode[STIX]{x1D706}_{KH}$
decreases, as intuitively expected.

Figure 7. The growth of gas boundary layer thickness (
![]() $\unicode[STIX]{x1D6FF}_{g}$
) along the axis (a); and comparison of the dimensionless wavenumber,
$\unicode[STIX]{x1D6FF}_{g}$
) along the axis (a); and comparison of the dimensionless wavenumber,
![]() $\unicode[STIX]{x03C0}D/\unicode[STIX]{x1D706}$
, obtained from the simulations, with the experimental data of Hoyt & Taylor (Reference Hoyt and Taylor1977) (b).
$\unicode[STIX]{x03C0}D/\unicode[STIX]{x1D706}$
, obtained from the simulations, with the experimental data of Hoyt & Taylor (Reference Hoyt and Taylor1977) (b).
Figure 7 compares the growth of the gas boundary layer thickness (
![]() $\unicode[STIX]{x1D6FF}_{g}$
) and the dimensionless wavenumber (
$\unicode[STIX]{x1D6FF}_{g}$
) and the dimensionless wavenumber (
![]() $\unicode[STIX]{x03C0}D/\unicode[STIX]{x1D706}$
) along the axis. The wavenumbers obtained from this computational fluid dynamics (CFD) study are compared with the experimental correlation obtained by Hoyt & Taylor (Reference Hoyt and Taylor1977) (figure 7
b). The experimental data of Hoyt & Taylor (Reference Hoyt and Taylor1977) were obtained much further downstream, between 40 to 200 diameters downstream of the nozzle and for a much smaller density ratio. Our CFD results lie very close to the line at
$\unicode[STIX]{x03C0}D/\unicode[STIX]{x1D706}$
) along the axis. The wavenumbers obtained from this computational fluid dynamics (CFD) study are compared with the experimental correlation obtained by Hoyt & Taylor (Reference Hoyt and Taylor1977) (figure 7
b). The experimental data of Hoyt & Taylor (Reference Hoyt and Taylor1977) were obtained much further downstream, between 40 to 200 diameters downstream of the nozzle and for a much smaller density ratio. Our CFD results lie very close to the line at
![]() $x/D>6.0$
, but the wavenumbers are larger closer to the nozzle. This suggests that the experimental correlation of Hoyt & Taylor (Reference Hoyt and Taylor1977) is not valid very close to the nozzle exit and that the higher
$x/D>6.0$
, but the wavenumbers are larger closer to the nozzle. This suggests that the experimental correlation of Hoyt & Taylor (Reference Hoyt and Taylor1977) is not valid very close to the nozzle exit and that the higher
![]() $\hat{\unicode[STIX]{x1D70C}}$
considered here results in smaller wavelengths. Hoyt & Taylor (Reference Hoyt and Taylor1977) also show that the wavenumber of the instability does not change significantly with
$\hat{\unicode[STIX]{x1D70C}}$
considered here results in smaller wavelengths. Hoyt & Taylor (Reference Hoyt and Taylor1977) also show that the wavenumber of the instability does not change significantly with
![]() $U_{r}$
, as also seen here.
$U_{r}$
, as also seen here.
The gas boundary layer thickness starts from about
![]() $0.1D$
and grows to twice the jet diameter, 10 diameters downstream of the nozzle. This growth is faster at lower
$0.1D$
and grows to twice the jet diameter, 10 diameters downstream of the nozzle. This growth is faster at lower
![]() $\hat{U}$
. The slight oscillations in the boundary layer thickness are due to the surface waves. The Reynolds and Weber numbers based on
$\hat{U}$
. The slight oscillations in the boundary layer thickness are due to the surface waves. The Reynolds and Weber numbers based on
![]() $\unicode[STIX]{x1D6FF}_{g}$
are
$\unicode[STIX]{x1D6FF}_{g}$
are
![]() $200<Re_{r,\unicode[STIX]{x1D6FF}}<360$
and
$200<Re_{r,\unicode[STIX]{x1D6FF}}<360$
and
![]() $20<We_{r,\unicode[STIX]{x1D6FF}}<70$
. The value of
$20<We_{r,\unicode[STIX]{x1D6FF}}<70$
. The value of
![]() $\unicode[STIX]{x1D6FF}_{g}$
changes between
$\unicode[STIX]{x1D6FF}_{g}$
changes between
![]() $20~\unicode[STIX]{x03BC}\text{m}$
to
$20~\unicode[STIX]{x03BC}\text{m}$
to
![]() $400~\unicode[STIX]{x03BC}\text{m}$
along the axis. With the current grid size of
$400~\unicode[STIX]{x03BC}\text{m}$
along the axis. With the current grid size of
![]() $2~\unicode[STIX]{x03BC}\text{m}$
, there is enough resolution to properly capture the velocity gradients inside the boundary layer. A more detailed mesh study was performed in our earlier study (Zandian et al.
Reference Zandian, Sirignano and Hussain2018), and will not be repeated here. It was shown that the current grid accurately captures the surface distortion and lobe tearing.
$2~\unicode[STIX]{x03BC}\text{m}$
, there is enough resolution to properly capture the velocity gradients inside the boundary layer. A more detailed mesh study was performed in our earlier study (Zandian et al.
Reference Zandian, Sirignano and Hussain2018), and will not be repeated here. It was shown that the current grid accurately captures the surface distortion and lobe tearing.

Figure 8. Temporal plot of
![]() $L_{t}/D$
and
$L_{t}/D$
and
![]() $L_{w}/D$
for case 1,
$L_{w}/D$
for case 1,
![]() $\hat{U}=0.1$
(a); case 2,
$\hat{U}=0.1$
(a); case 2,
![]() $\hat{U}=0.2$
(b); and case 3,
$\hat{U}=0.2$
(b); and case 3,
![]() $\hat{U}=0.5$
(c). The solid line indicates simple convection with Dimotakis velocity.
$\hat{U}=0.5$
(c). The solid line indicates simple convection with Dimotakis velocity.
The axial length of the jet tip (
![]() $L_{t}$
) and the fetch from the jet exit of the first surface wave in the UR region (
$L_{t}$
) and the fetch from the jet exit of the first surface wave in the UR region (
![]() $L_{w}$
) for cases 1–3 are compared in time in figure 8(a–c). All lengths are measured from the injection plane and non-dimensionalized by the jet diameter. The average velocity of each segment (in terms of the fraction of
$L_{w}$
) for cases 1–3 are compared in time in figure 8(a–c). All lengths are measured from the injection plane and non-dimensionalized by the jet diameter. The average velocity of each segment (in terms of the fraction of
![]() $U_{l}$
) is also shown on the plots. The solid lines (
$U_{l}$
) is also shown on the plots. The solid lines (
![]() $L_{D}$
) indicate the simple convection of the first perturbation with the Dimotakis speed (Dimotakis Reference Dimotakis1986),
$L_{D}$
) indicate the simple convection of the first perturbation with the Dimotakis speed (Dimotakis Reference Dimotakis1986),
![]() $U_{D}=(U_{l}+\sqrt{\hat{\unicode[STIX]{x1D70C}}}U_{g})/(1+\sqrt{\hat{\unicode[STIX]{x1D70C}}})$
. The Dimotakis speed is the convection speed of a fully formed KH wave at its base. This speed is found to be
$U_{D}=(U_{l}+\sqrt{\hat{\unicode[STIX]{x1D70C}}}U_{g})/(1+\sqrt{\hat{\unicode[STIX]{x1D70C}}})$
. The Dimotakis speed is the convection speed of a fully formed KH wave at its base. This speed is found to be
![]() $U_{D}=41.75~\text{m}~\text{s}^{-1}$
,
$U_{D}=41.75~\text{m}~\text{s}^{-1}$
,
![]() $42.7~\text{m}~\text{s}^{-1}$
and
$42.7~\text{m}~\text{s}^{-1}$
and
![]() $45~\text{m}~\text{s}^{-1}$
, for cases 1, 2 and 3, respectively. Time has been non-dimensionalized by the Dimotakis velocity and the jet diameter (
$45~\text{m}~\text{s}^{-1}$
, for cases 1, 2 and 3, respectively. Time has been non-dimensionalized by the Dimotakis velocity and the jet diameter (
![]() $t^{\ast }=U_{D}t/D$
).
$t^{\ast }=U_{D}t/D$
).
In all cases, the wave speed follows
![]() $U_{D}$
at early times after the wave appearance, but it diverges and becomes slightly larger at later times. This divergence is more apparent at lower
$U_{D}$
at early times after the wave appearance, but it diverges and becomes slightly larger at later times. This divergence is more apparent at lower
![]() $\hat{U}$
. The tip velocity (
$\hat{U}$
. The tip velocity (
![]() $U_{t}$
) is always smaller than the wave speed (
$U_{t}$
) is always smaller than the wave speed (
![]() $U_{w}$
) due to the higher drag force caused by the stagnant gas ahead of the cap. Therefore, the KH waves that form in the UR eventually enter the BCR and catch up with the tip. The rate at which the KH waves reach the tip is directly proportional to the difference between the tip speed and the wave speed. The wave speed only increases slightly with the increase of
$U_{w}$
) due to the higher drag force caused by the stagnant gas ahead of the cap. Therefore, the KH waves that form in the UR eventually enter the BCR and catch up with the tip. The rate at which the KH waves reach the tip is directly proportional to the difference between the tip speed and the wave speed. The wave speed only increases slightly with the increase of
![]() $U_{g}$
because it is mainly proportional to
$U_{g}$
because it is mainly proportional to
![]() $U_{l}$
especially at such low density ratio; see the definition of
$U_{l}$
especially at such low density ratio; see the definition of
![]() $U_{D}$
. The tip velocity, however, increases more significantly with increasing
$U_{D}$
. The tip velocity, however, increases more significantly with increasing
![]() $U_{g}$
. Therefore,
$U_{g}$
. Therefore,
![]() $U_{w}-U_{t}$
becomes smaller at higher
$U_{w}-U_{t}$
becomes smaller at higher
![]() $\hat{U}$
and thus it takes a longer time for the UR waves to reach the cap. The KH vortex leaves the interface upon merging and the wave disappears afterwards. This happens at
$\hat{U}$
and thus it takes a longer time for the UR waves to reach the cap. The KH vortex leaves the interface upon merging and the wave disappears afterwards. This happens at
![]() $t^{\ast }=13$
for
$t^{\ast }=13$
for
![]() $\hat{U}=0.1$
, and at
$\hat{U}=0.1$
, and at
![]() $t^{\ast }=15.5$
for
$t^{\ast }=15.5$
for
![]() $\hat{U}=0.2$
. For
$\hat{U}=0.2$
. For
![]() $\hat{U}=0.5$
, this catch-up is so slow that the cap moves out of the computational box before the KH wave reaches it. Later it is shown that the liquid-jet breakup occurs faster at lower
$\hat{U}=0.5$
, this catch-up is so slow that the cap moves out of the computational box before the KH wave reaches it. Later it is shown that the liquid-jet breakup occurs faster at lower
![]() $\hat{U}$
. In those ranges (cases 1 and 2), the wave crest breaks into ligaments and droplets before it reaches the cap. In case 3, however, the wave does not have enough time to completely break up before reaching the cap.
$\hat{U}$
. In those ranges (cases 1 and 2), the wave crest breaks into ligaments and droplets before it reaches the cap. In case 3, however, the wave does not have enough time to completely break up before reaching the cap.

Figure 9. Liquid-jet surface for case 1 (a); case 2 (b); and case 3 (c) at
![]() $t^{\ast }=11.25$
.
$t^{\ast }=11.25$
.
The higher tip speed for higher
![]() $\hat{U}$
also implies that with increasing cap speed, less mass accumulates at the cap; hence, the cap size decreases. This is clearly delineated in figure 9, where the liquid jet for cases 1–3 are compared at the same time,
$\hat{U}$
also implies that with increasing cap speed, less mass accumulates at the cap; hence, the cap size decreases. This is clearly delineated in figure 9, where the liquid jet for cases 1–3 are compared at the same time,
![]() $t^{\ast }=11.25$
. The wavelengths are larger for case 3, but the cap is noticeably smaller. Also noticeable is that the three-dimensionality in the surface waves is delayed as
$t^{\ast }=11.25$
. The wavelengths are larger for case 3, but the cap is noticeably smaller. Also noticeable is that the three-dimensionality in the surface waves is delayed as
![]() $\hat{U}$
increases, and the lobe formation and breakup occur much later.
$\hat{U}$
increases, and the lobe formation and breakup occur much later.
When the UR waves get into the BCR, their roll-up direction changes since the relative gas–liquid velocity is the opposite downstream of the wave (the gas moves faster than the liquid). This phenomenon is clearly shown in figure 10, where the KH wave indicated by the black arrow faces upstream at
![]() $t^{\ast }=10.5$
while it is in the UR, becomes neutral as it enters the BCR boundary at
$t^{\ast }=10.5$
while it is in the UR, becomes neutral as it enters the BCR boundary at
![]() $t^{\ast }=11$
, and faces downstream in the BCR at
$t^{\ast }=11$
, and faces downstream in the BCR at
![]() $t^{\ast }=11.5$
. Taking a control volume that encompasses the entire wave with both upstream and downstream troughs, the formation of a negative circulation just downstream of the wave overcomes the opposite circulation of the KH vortex on the upstream side, as the wave enters the BCR in figure 10(b). As the wave proceeds in the BCR, this negative circulation builds up and rolls the wave backwards towards the cap (figure 10
c).
$t^{\ast }=11.5$
. Taking a control volume that encompasses the entire wave with both upstream and downstream troughs, the formation of a negative circulation just downstream of the wave overcomes the opposite circulation of the KH vortex on the upstream side, as the wave enters the BCR in figure 10(b). As the wave proceeds in the BCR, this negative circulation builds up and rolls the wave backwards towards the cap (figure 10
c).

Figure 10. Change in the roll-up direction of the KH wave as it moves from the UR to the BCR region in case 2, at
![]() $t^{\ast }=10.5$
(a);
$t^{\ast }=10.5$
(a);
![]() $t^{\ast }=11.0$
(b); and
$t^{\ast }=11.0$
(b); and
![]() $t^{\ast }=11.5$
(c).
$t^{\ast }=11.5$
(c).
3.3 Vortex-surface interactions
The liquid jet at a time before the appearance of the perturbations is shown in figure 11(a). The vortex structures indicated by the
![]() $\unicode[STIX]{x1D706}_{2}$
isosurface are also shown in the same figure, at the same time step; figure 11(b). The vortices in the vicinity of the cap include the ‘tip vortex’ that covers the front of the cap, caused by the gas flow around the mushroom-shaped cap, and a ‘rim vortex’ ring that is shed from the cap by the ring’s own self-advection. As discussed earlier, there are two sets of oppositely oriented KH vortex rings on the stem of the jet, which are formed due to the shear caused by the entrained gas which moves in the downstream and upstream directions. The KH vortices deform and take a hairpin shape before the jet surface is deformed. Figure 12 shows that the first liquid lobes are formed at the exact same location where the KH vortices are turned streamwise and create a hairpin structure at a later time. This conveys that the vortex dynamics drives the surface dynamics, as was first identified by Jarrahbashi et al. (Reference Jarrahbashi, Sirignano, Popov and Hussain2016) and ZSH2. Even though both those studies were temporal with periodic conditions on a liquid segment, our spatial results show that the temporal study of vortex dynamics can capture well the mechanisms in the UR region, where similar physical behaviours occur.
$\unicode[STIX]{x1D706}_{2}$
isosurface are also shown in the same figure, at the same time step; figure 11(b). The vortices in the vicinity of the cap include the ‘tip vortex’ that covers the front of the cap, caused by the gas flow around the mushroom-shaped cap, and a ‘rim vortex’ ring that is shed from the cap by the ring’s own self-advection. As discussed earlier, there are two sets of oppositely oriented KH vortex rings on the stem of the jet, which are formed due to the shear caused by the entrained gas which moves in the downstream and upstream directions. The KH vortices deform and take a hairpin shape before the jet surface is deformed. Figure 12 shows that the first liquid lobes are formed at the exact same location where the KH vortices are turned streamwise and create a hairpin structure at a later time. This conveys that the vortex dynamics drives the surface dynamics, as was first identified by Jarrahbashi et al. (Reference Jarrahbashi, Sirignano, Popov and Hussain2016) and ZSH2. Even though both those studies were temporal with periodic conditions on a liquid segment, our spatial results show that the temporal study of vortex dynamics can capture well the mechanisms in the UR region, where similar physical behaviours occur.

Figure 11. Liquid-jet surface near the cap (a); and vortices indicated by
![]() $\unicode[STIX]{x1D706}_{2}=-10^{11}~\text{s}^{-2}$
isosurface (b), at
$\unicode[STIX]{x1D706}_{2}=-10^{11}~\text{s}^{-2}$
isosurface (b), at
![]() $t^{\ast }=3.0$
in case 2.
$t^{\ast }=3.0$
in case 2.

Figure 12. Liquid jet surface at
![]() $t^{\ast }=3.5$
in case 2.
$t^{\ast }=3.5$
in case 2.
Figure 13 shows the liquid jet and its vortices at
![]() $t^{\ast }=4.5$
in case 1. The KH vortex rings start from an axisymmetric form and grow and deform as they advect downstream. Following this change in the KH vortex structure, the initially axisymmetric KH waves (closer to the nozzle) also become more corrugated as they move downstream. The mode number (azimuthal wavelength) of the lobes is directly related to the number of counter-rotating streamwise vortex pairs that form as the KH vortices become streamwise oriented. Thus, a detailed analysis of the causes of streamwise vortex generation and its growth can explain much regarding the future behaviour of the lobes and their breakup mechanism and the size of ligaments and droplets. This analysis is discussed in § 3.5.
$t^{\ast }=4.5$
in case 1. The KH vortex rings start from an axisymmetric form and grow and deform as they advect downstream. Following this change in the KH vortex structure, the initially axisymmetric KH waves (closer to the nozzle) also become more corrugated as they move downstream. The mode number (azimuthal wavelength) of the lobes is directly related to the number of counter-rotating streamwise vortex pairs that form as the KH vortices become streamwise oriented. Thus, a detailed analysis of the causes of streamwise vortex generation and its growth can explain much regarding the future behaviour of the lobes and their breakup mechanism and the size of ligaments and droplets. This analysis is discussed in § 3.5.

Figure 13. Liquid-jet surface (a); and vortex structures indicated by
![]() $\unicode[STIX]{x1D706}_{2}=-10^{11}~\text{s}^{-2}$
isosurface (b) at
$\unicode[STIX]{x1D706}_{2}=-10^{11}~\text{s}^{-2}$
isosurface (b) at
![]() $t^{\ast }=4.5$
in case 1.
$t^{\ast }=4.5$
in case 1.
Figure 14. Liquid-jet surface and the axial vorticity (
![]() $\unicode[STIX]{x1D714}_{x}$
) contours on the plane intersecting the jet at
$\unicode[STIX]{x1D714}_{x}$
) contours on the plane intersecting the jet at
![]() $x/D=2.0$
at
$x/D=2.0$
at
![]() $t^{\ast }=4.5$
in case 1.
$t^{\ast }=4.5$
in case 1.
The axial vorticity (
![]() $\unicode[STIX]{x1D714}_{x}$
) contours on a spanwise plane intersecting with the liquid jet stem at
$\unicode[STIX]{x1D714}_{x}$
) contours on a spanwise plane intersecting with the liquid jet stem at
![]() $x/D=2.0$
and
$x/D=2.0$
and
![]() $x/D=2.25$
at
$x/D=2.25$
at
![]() $t^{\ast }=4.5$
(same time as figure 13) are shown in figures 14 and 15, respectively. The plane in figure 14 cuts the jet at the braid of one of the newer KH waves slightly upstream of the former wave that is located at
$t^{\ast }=4.5$
(same time as figure 13) are shown in figures 14 and 15, respectively. The plane in figure 14 cuts the jet at the braid of one of the newer KH waves slightly upstream of the former wave that is located at
![]() $x/D=2.25$
and is the subject of figure 15. Two layers of counter-rotating streamwise vorticity are seen in figure 14. The inner layer closer to the liquid surface is the hairpin vortex ring with seven pairs of counter-rotating axial vortices which are indicated by the pair of single arrows. This hairpin stretches upstream and over the next consecutive KH wave upstream of the current wave, similar to what was described by ZSH2. Right on the outer side of this vorticity layer is another layer of counter-rotating vorticity, a pair of which is shown by the double-lined arrows. Since these counter-rotating vortex pairs are
$x/D=2.25$
and is the subject of figure 15. Two layers of counter-rotating streamwise vorticity are seen in figure 14. The inner layer closer to the liquid surface is the hairpin vortex ring with seven pairs of counter-rotating axial vortices which are indicated by the pair of single arrows. This hairpin stretches upstream and over the next consecutive KH wave upstream of the current wave, similar to what was described by ZSH2. Right on the outer side of this vorticity layer is another layer of counter-rotating vorticity, a pair of which is shown by the double-lined arrows. Since these counter-rotating vortex pairs are
![]() $180^{\circ }$
out of phase with respect to the inner layer, it is concluded that this layer belongs to another hairpin vortex layer with opposite direction. This layer is called the outer hairpin layer and is stretched downstream and underneath the next downstream KH wave, shown in figure 15. The reason why much axial deflection is still not seen in this vortex ring in figure 13 is that the
$180^{\circ }$
out of phase with respect to the inner layer, it is concluded that this layer belongs to another hairpin vortex layer with opposite direction. This layer is called the outer hairpin layer and is stretched downstream and underneath the next downstream KH wave, shown in figure 15. The reason why much axial deflection is still not seen in this vortex ring in figure 13 is that the
![]() $\unicode[STIX]{x1D714}_{x}$
magnitude is two orders of magnitude smaller than the azimuthal vorticity (
$\unicode[STIX]{x1D714}_{x}$
magnitude is two orders of magnitude smaller than the azimuthal vorticity (
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) magnitude at this time, as will be shown in § 3.5. Even though the vorticity layers are not very neat and organized at all azimuthal locations of this picture, seven counter-rotating vortex pairs are distinguished and marked, which indicates that seven lobes are expected to form on this KH wave at a later time.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) magnitude at this time, as will be shown in § 3.5. Even though the vorticity layers are not very neat and organized at all azimuthal locations of this picture, seven counter-rotating vortex pairs are distinguished and marked, which indicates that seven lobes are expected to form on this KH wave at a later time.

Figure 15. Liquid-jet surface and the axial vorticity (
![]() $\unicode[STIX]{x1D714}_{x}$
) contours on the plane intersecting the jet at
$\unicode[STIX]{x1D714}_{x}$
) contours on the plane intersecting the jet at
![]() $x/D=2.25$
at
$x/D=2.25$
at
![]() $t^{\ast }=4.5$
in case 1.
$t^{\ast }=4.5$
in case 1.
In the downstream cross-sectional plane of figure 15, three counter-rotating vorticity layers are observed. The outer layer, indicated by a pair of thick arrows, is the ‘outer hairpin’ vortex layer for this new wave which stretches downstream. This hairpin layer is right on the outer surface of the KH wave and the liquid sheet. Right on the inner side of this wave, there is another layer of counter-rotating hairpin, marked by a pair of double-lined arrows and indicated as the ‘inner hairpin’ layer. This layer is the same outer hairpin layer seen in figure 14 which is now stretched underneath the wave shown in figure 15. A comparison between the counter-rotating vortex pairs of these two layers shows that they both belong to different sections of the same hairpin structure that wraps around the upstream wave and under the next downstream wave. There is another vortex ring on the inner side of this hairpin, which is less organized and more chaotic, but with smaller axial vorticity component, marked by a pair of thin arrows. This layer is part of the slightly deflected KH vortex located underneath the liquid sheet.

Figure 16. Three-dimensional schematics showing the overlapping of the two hairpin vortices – one from the lobe crest (outer black tube, pointing downstream), and the other from the braid (inner red tube, pointing upstream) (a);
![]() $A$
is the plane in which (b) is drawn; cross-sectional view of the
$A$
is the plane in which (b) is drawn; cross-sectional view of the
![]() $A$
-plane, showing the thinning of the lobe sheet due to the combined induction of the two oppositely orientated overlapping hairpins (b). The vortex schematics are periodic in
$A$
-plane, showing the thinning of the lobe sheet due to the combined induction of the two oppositely orientated overlapping hairpins (b). The vortex schematics are periodic in
![]() $x$
- and
$x$
- and
![]() $y$
-directions (ZSH2).
$y$
-directions (ZSH2).
The location and configuration of the axial counter-rotating vortex pairs described here are in line with the vortex structures depicted by ZSH2 for a planar sheet, repeated schematically in figure 16. Even though those vortex structures were identified for a planar liquid jet, the simulation results shown in figures 14 and 15 hint that a similar pattern also exists for round jets. Following the structure of vortices sketched in figure 16 and their induced gas flow, a subsequent thinning and perforation is expected to follow at the centre of the lobes.
The effects of the counter-rotating axial vortex pairs shown in figures 14 and 15 are clearer at a later time (
![]() $t^{\ast }=5$
) shown in figure 17. When
$t^{\ast }=5$
) shown in figure 17. When
![]() $\unicode[STIX]{x1D714}_{x}$
grows enough to become comparable to
$\unicode[STIX]{x1D714}_{x}$
grows enough to become comparable to
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
, 3-D instabilities occur and the vortices become asymmetric. This phenomenon creates corrugations in the KH vortex ring and also larger axial stretch on the hairpin vortices that are also stretched by the KH vortex. The corrugated KH vortex and the hairpin vortex that stretches over it are shown in figure 17. The inner hairpin vortex is not clearly seen in this picture since the KH vortex and the liquid lobes on the outer side of this hairpin block those hairpins from the view. As described by ZSH2 and depicted in figure 16, overlapping of these oppositely oriented counter-rotating hairpins, that are on the outer and inner sides of the lobe, thins the lobe at its centre and perforates the lobes. Thinning of the lobes (wave) can be clearly seen in the cross-sectional view of the plane illustrated in figure 15.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
, 3-D instabilities occur and the vortices become asymmetric. This phenomenon creates corrugations in the KH vortex ring and also larger axial stretch on the hairpin vortices that are also stretched by the KH vortex. The corrugated KH vortex and the hairpin vortex that stretches over it are shown in figure 17. The inner hairpin vortex is not clearly seen in this picture since the KH vortex and the liquid lobes on the outer side of this hairpin block those hairpins from the view. As described by ZSH2 and depicted in figure 16, overlapping of these oppositely oriented counter-rotating hairpins, that are on the outer and inner sides of the lobe, thins the lobe at its centre and perforates the lobes. Thinning of the lobes (wave) can be clearly seen in the cross-sectional view of the plane illustrated in figure 15.
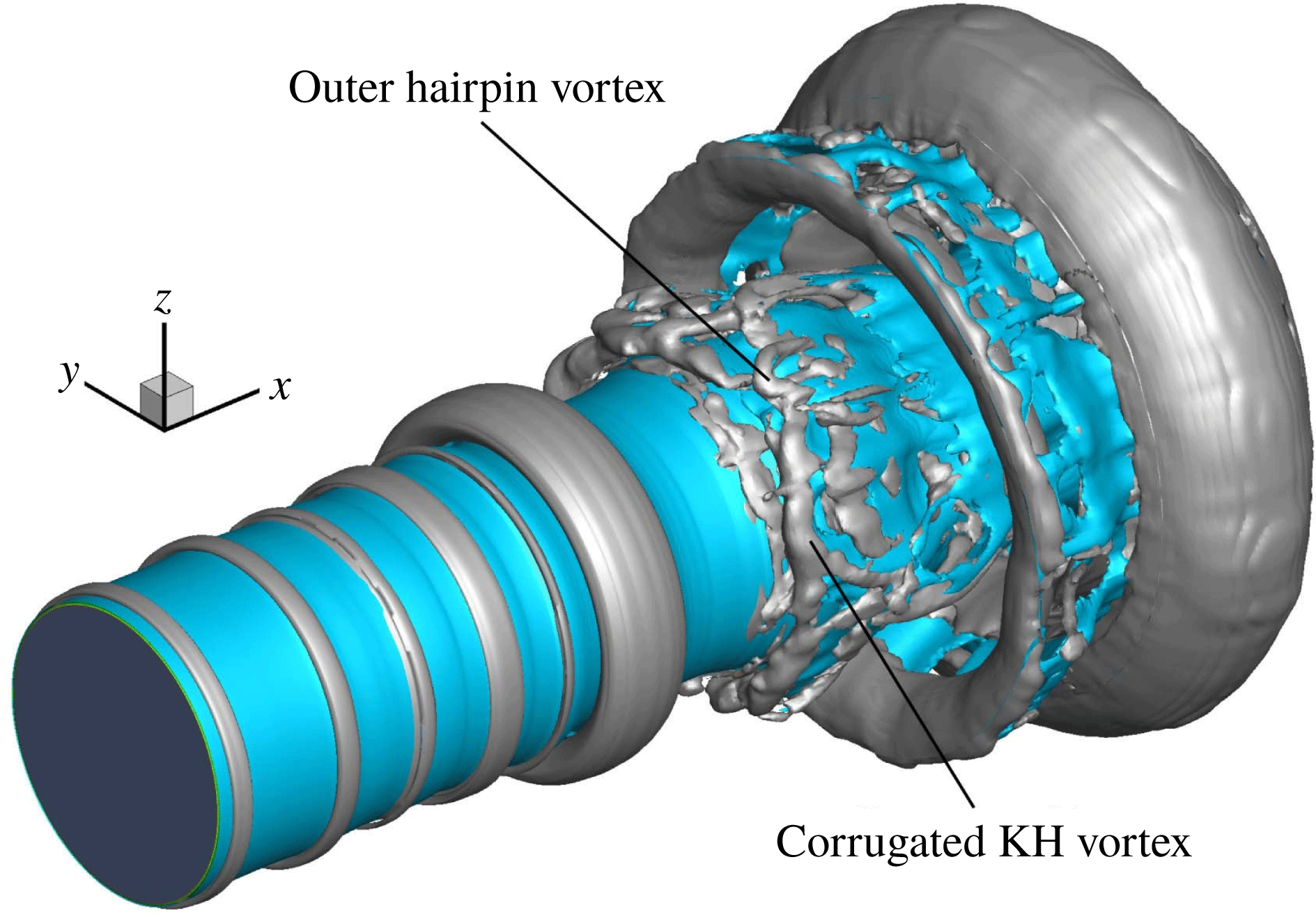
Figure 17. Liquid-jet surface (blue) and vortex structures (grey) at
![]() $t^{\ast }=5.0$
in case 1.
$t^{\ast }=5.0$
in case 1.

Figure 18. Liquid-jet surface at
![]() $t^{\ast }=5.5$
in case 1.
$t^{\ast }=5.5$
in case 1.
Following the same wave at a later time (
![]() $t^{\ast }=5.5$
), shown in figure 18, holes form on the lobes and expand as the lobes get stretched in the axial direction. The liquid bridges that are formed around the lobe rim finally break and create the first ligaments, which then break into droplets or detach from the jet core. Figure 18 also shows that there are in fact seven liquid lobes on each KH wave, as was inferred earlier by the number of counter-rotating axial vorticity pairs. Four of these lobes are already seen in this figure, and the other three are on the hidden side. Following the jet structure in time (
$t^{\ast }=5.5$
), shown in figure 18, holes form on the lobes and expand as the lobes get stretched in the axial direction. The liquid bridges that are formed around the lobe rim finally break and create the first ligaments, which then break into droplets or detach from the jet core. Figure 18 also shows that there are in fact seven liquid lobes on each KH wave, as was inferred earlier by the number of counter-rotating axial vorticity pairs. Four of these lobes are already seen in this figure, and the other three are on the hidden side. Following the jet structure in time (
![]() $t^{\ast }=8.5$
shown in figure 19), the same hole formation and breakup mechanism repeats. This qualitatively suggests that the breakup mechanism on the jet stem in the UR is periodic and occurs until the waves reach the BCR and break into droplets and/or coalesce with the cap. This substantiates the temporal studies of JS, Jarrahbashi et al. (Reference Jarrahbashi, Sirignano, Popov and Hussain2016), ZSH1 and ZSH2. The formation of holes on the rim of the jet cap (figure 18) is also conjectured to follow the same vortex mechanism, where the overlapping vortices are the tip vortex and the downstream KH vortex (figure 11) as it runs along the inner side of the cap; however, these vortex structures are much harder to capture and follow, and are not analysed in this study.
$t^{\ast }=8.5$
shown in figure 19), the same hole formation and breakup mechanism repeats. This qualitatively suggests that the breakup mechanism on the jet stem in the UR is periodic and occurs until the waves reach the BCR and break into droplets and/or coalesce with the cap. This substantiates the temporal studies of JS, Jarrahbashi et al. (Reference Jarrahbashi, Sirignano, Popov and Hussain2016), ZSH1 and ZSH2. The formation of holes on the rim of the jet cap (figure 18) is also conjectured to follow the same vortex mechanism, where the overlapping vortices are the tip vortex and the downstream KH vortex (figure 11) as it runs along the inner side of the cap; however, these vortex structures are much harder to capture and follow, and are not analysed in this study.

Figure 19. Liquid-jet surface at
![]() $t^{\ast }=8.5$
in case 1.
$t^{\ast }=8.5$
in case 1.
The step-by-step thinning of the lobes and the formation of holes and bridges on the stem of the jet are illustrated in the top row of figure 20. In the bottom row of the same figure 20(b), the vortex structures involved in the hole formation are depicted, where the overlapping of the two oppositely oriented hairpin vortices is seen. The chosen frame of figure 20 is more than
![]() $5D$
away from the jet cap, and shows that three-dimensionality on the vortex structures also develops on the stem (in the UR) and is independent of the BCR vortices.
$5D$
away from the jet cap, and shows that three-dimensionality on the vortex structures also develops on the stem (in the UR) and is independent of the BCR vortices.

Figure 20. Step-by-step tracking of hole formation mechanism in case 1. Liquid surface on a thinning lobe subject to hole formation (a); vortex structures indicated by
![]() $\unicode[STIX]{x1D706}_{2}=-10^{11}~\text{s}^{-2}$
isosurface on the same frame as ‘
$\unicode[STIX]{x1D706}_{2}=-10^{11}~\text{s}^{-2}$
isosurface on the same frame as ‘
![]() $a$
’ (b). Time is indicated at the top of each column.
$a$
’ (b). Time is indicated at the top of each column.
Even though these hairpins develop later than the BCR, they are much more important in the steady atomization process than the vortices shed from the cap, because the cap occurs only at the start of the jet and most of the breakup occurs in its absence. This is contrary to the claim of Shinjo & Umemura (Reference Shinjo and Umemura2010), who believed that (in the same range of
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
as ours) the primary atomization is mainly governed by the vortices shed from the cap and fed upstream through the gas. The hole formation was also claimed by them to be inertia driven and due to the collision of droplets on the lobes as they move upstream (Shinjo & Umemura Reference Shinjo and Umemura2010).
$We_{g}$
as ours) the primary atomization is mainly governed by the vortices shed from the cap and fed upstream through the gas. The hole formation was also claimed by them to be inertia driven and due to the collision of droplets on the lobes as they move upstream (Shinjo & Umemura Reference Shinjo and Umemura2010).
The hole formation mechanism prevails in case 1 and is the dominant cause of ligament and droplet formation. In case 2, the same mechanism is seen, but not as often as in case 1. The hole formation is delayed and there are fewer holes, bridges and ligaments in this case. This means that the hole formation is suppressed by increasing
![]() $\hat{U}$
. When
$\hat{U}$
. When
![]() $\hat{U}$
increases, the relative gas–liquid inertia decreases while the surface tension forces remain constant. At the same time, the viscous forces (
$\hat{U}$
increases, the relative gas–liquid inertia decreases while the surface tension forces remain constant. At the same time, the viscous forces (
![]() $\propto \unicode[STIX]{x1D707}_{l}U_{r}/D$
) also diminish but not as significantly as the inertia. Above some critical
$\propto \unicode[STIX]{x1D707}_{l}U_{r}/D$
) also diminish but not as significantly as the inertia. Above some critical
![]() $\hat{U}$
, the inertia force is not strong enough to overcome the surface tension forces that resist the perforation of the lobe; therefore, the hole formation is suppressed or delayed. Also, the higher strength of the viscous forces compared to the inertia results in less stretching of the lobes. Therefore, the three-dimensionality occurs later at higher
$\hat{U}$
, the inertia force is not strong enough to overcome the surface tension forces that resist the perforation of the lobe; therefore, the hole formation is suppressed or delayed. Also, the higher strength of the viscous forces compared to the inertia results in less stretching of the lobes. Therefore, the three-dimensionality occurs later at higher
![]() $\hat{U}$
and the KH waves remain axisymmetric for a longer time, as was seen in figure 9. The same story applies to the vortices, where less axial stretching is seen in the KH vortex rings; see figure 21.
$\hat{U}$
and the KH waves remain axisymmetric for a longer time, as was seen in figure 9. The same story applies to the vortices, where less axial stretching is seen in the KH vortex rings; see figure 21.

Figure 21. The vortex structures in case 3 at
![]() $t^{\ast }=11.25$
(same time as in figure 9
c).
$t^{\ast }=11.25$
(same time as in figure 9
c).
Figure 9 also shows that the azimuthal mode number has decreased from seven in case 1, to four in case 3. Four liquid lobes are seen in figure 9(c) – one in the front view, one on top, one on bottom and one on the rear view which cannot be seen here. These lobes follow the four axial pairs of hairpin vortices that are forming there, shown in figure 21. The change in the azimuthal mode number (wavelength) against
![]() $\hat{U}$
is in very good agreement with the expression provided by Shinjo & Umemura (Reference Shinjo and Umemura2011) for jet flow in quiescent gas. They found that
$\hat{U}$
is in very good agreement with the expression provided by Shinjo & Umemura (Reference Shinjo and Umemura2011) for jet flow in quiescent gas. They found that
![]() $\unicode[STIX]{x1D706}_{\bot }\propto 1/U_{l}$
, which for a coaxial jet can be modified to
$\unicode[STIX]{x1D706}_{\bot }\propto 1/U_{l}$
, which for a coaxial jet can be modified to
![]() $\unicode[STIX]{x1D706}_{\bot }\propto 1/U_{r}$
. Following this expression,
$\unicode[STIX]{x1D706}_{\bot }\propto 1/U_{r}$
. Following this expression,
Using our simulation results, we get
where
![]() $n$
is the azimuthal mode number, found to be seven and four for cases 1 and 3, respectively. The difference between the two results is 2.7 %, which is negligible.
$n$
is the azimuthal mode number, found to be seven and four for cases 1 and 3, respectively. The difference between the two results is 2.7 %, which is negligible.
The lobes, ligaments and cap rim are much thicker for case 3 compared to lower
![]() $\hat{U}$
cases. Because of this thickening, the lobes do not thin as easily and are stretched directly but more slowly into thick ligaments. This conveys the transition of the cascade process from domain II (hole formation) to domain I (lobe stretching) as was introduced by ZSH1. This transition was attributed to the lowering of
$\hat{U}$
cases. Because of this thickening, the lobes do not thin as easily and are stretched directly but more slowly into thick ligaments. This conveys the transition of the cascade process from domain II (hole formation) to domain I (lobe stretching) as was introduced by ZSH1. This transition was attributed to the lowering of
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
in the study of ZSH1 where no coaxial flow was considered. This further supports the claim that the Reynolds and Weber numbers in coaxial jets should be based on the relative gas–liquid velocity rather than just the liquid-jet velocity.
$We_{g}$
in the study of ZSH1 where no coaxial flow was considered. This further supports the claim that the Reynolds and Weber numbers in coaxial jets should be based on the relative gas–liquid velocity rather than just the liquid-jet velocity.

Figure 22. Identification of domains I and II on a
![]() $We_{r}$
–
$We_{r}$
–
![]() $Re_{r}$
diagram. The case numbers are indicated by the symbols. The approximate transitional zone has been denoted by the grey stripe.
$Re_{r}$
diagram. The case numbers are indicated by the symbols. The approximate transitional zone has been denoted by the grey stripe.
![]() $U_{r}$
decreases with increasing
$U_{r}$
decreases with increasing
![]() $\hat{U}$
, which results in a decrease in
$\hat{U}$
, which results in a decrease in
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
. This decrease in
$We_{r}$
. This decrease in
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
is consistent with the shifting from the hole formation breakup (domain II) to the lobe stretching process (domain I), as predicted by ZSH1 and shown schematically in figure 22. For the given values of
$We_{r}$
is consistent with the shifting from the hole formation breakup (domain II) to the lobe stretching process (domain I), as predicted by ZSH1 and shown schematically in figure 22. For the given values of
![]() $We_{r}$
and
$We_{r}$
and
![]() $Re_{r}$
, a round jet with no coaxial gas flow would belong to domain I (ZSH1), without formation of holes. However, our results show that cases 1 and 2 follow the hole formation cascade process which belongs to domain II at higher ranges of
$Re_{r}$
, a round jet with no coaxial gas flow would belong to domain I (ZSH1), without formation of holes. However, our results show that cases 1 and 2 follow the hole formation cascade process which belongs to domain II at higher ranges of
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
. Therefore, our conclusion is that the addition of coaxial gas flow shifts the transitional boundary between the two domains. We have marked the approximate location of the transitional boundary by the grey stripe in figure 22. If the
$We_{g}$
. Therefore, our conclusion is that the addition of coaxial gas flow shifts the transitional boundary between the two domains. We have marked the approximate location of the transitional boundary by the grey stripe in figure 22. If the
![]() $We_{r}$
–
$We_{r}$
–
![]() $Re_{r}$
diagram, figure 22, is placed within the general regime diagram of Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000), it is seen that
$Re_{r}$
diagram, figure 22, is placed within the general regime diagram of Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000), it is seen that
![]() $We_{r}=0$
(
$We_{r}=0$
(
![]() $U_{g}=U_{l}$
) represents a boundary between pressure and air-blast atomization. On the other hand, when
$U_{g}=U_{l}$
) represents a boundary between pressure and air-blast atomization. On the other hand, when
![]() $We_{r}$
is large (
$We_{r}$
is large (
![]() $U_{g}=0$
or very small) the line of viscosity affected to inertial breakup is crossed at a certain
$U_{g}=0$
or very small) the line of viscosity affected to inertial breakup is crossed at a certain
![]() $Re_{r}$
, which would correspond to the grey shaded transitional zone. Even though finding the exact boundary between the domains is not the objective of this study (it requires many computationally expensive simulations), it encourages a more thorough analysis of the effects of
$Re_{r}$
, which would correspond to the grey shaded transitional zone. Even though finding the exact boundary between the domains is not the objective of this study (it requires many computationally expensive simulations), it encourages a more thorough analysis of the effects of
![]() $U_{r}$
on the atomization process to generalize the breakup mechanisms formerly developed for non-coaxial jet flows.
$U_{r}$
on the atomization process to generalize the breakup mechanisms formerly developed for non-coaxial jet flows.
Figure 23. Kinematic variation of the normalized
![]() $\unicode[STIX]{x1D714}_{x}$
(a);
$\unicode[STIX]{x1D714}_{x}$
(a);
![]() $\unicode[STIX]{x1D714}_{r}$
(b); and
$\unicode[STIX]{x1D714}_{r}$
(b); and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(c) for different velocity ratios.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(c) for different velocity ratios.
3.4 Temporal versus spatial vorticity measurements
JS and ZSH2 showed that the development of 3-D instabilities and lobe formation are directly related to the formation of streamwise (axial) vorticity,
![]() $\unicode[STIX]{x1D714}_{x}$
, on the liquid jet surface. The higher and faster growth of
$\unicode[STIX]{x1D714}_{x}$
, on the liquid jet surface. The higher and faster growth of
![]() $\unicode[STIX]{x1D714}_{x}$
(compared to
$\unicode[STIX]{x1D714}_{x}$
(compared to
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) represents itself as the earlier deformation of the surface and the development of asymmetric liquid structures; e.g. lobes and ligaments. In this section, the three vorticity components (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) represents itself as the earlier deformation of the surface and the development of asymmetric liquid structures; e.g. lobes and ligaments. In this section, the three vorticity components (
![]() $\unicode[STIX]{x1D714}_{x}$
,
$\unicode[STIX]{x1D714}_{x}$
,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
and
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
and
![]() $\unicode[STIX]{x1D714}_{r}$
) are measured for cases 1–3 both in temporal and spatial frames of reference to show the effects of
$\unicode[STIX]{x1D714}_{r}$
) are measured for cases 1–3 both in temporal and spatial frames of reference to show the effects of
![]() $\hat{U}$
on streamwise vorticity generation. A comparison between vorticity along the axis in an Eulerian frame versus a frame fixed to a surface wave is presented at the end of this section to delineate the consistency and discrepancies between the two results and to draw the major conclusions regarding the periodicity of the surface deformation.
$\hat{U}$
on streamwise vorticity generation. A comparison between vorticity along the axis in an Eulerian frame versus a frame fixed to a surface wave is presented at the end of this section to delineate the consistency and discrepancies between the two results and to draw the major conclusions regarding the periodicity of the surface deformation.
Figure 23 compares the kinematic variation of the three vorticity components for cases 1–3. To obtain these results, one of the waves formed at an early time is chosen and is followed in time. The absolute value of the vorticity components are integrated and averaged (volumetric average) in the vicinity of the wave in a control volume (frame) moving with the wave speed. In these plots, the vorticity components are normalized by the maximum azimuthal vorticity (
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
) which occurs near the nozzle exit for each case. The value of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
) which occurs near the nozzle exit for each case. The value of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
is found to be in the order of gas–liquid velocity difference divided by the gas vorticity layer thickness (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
is found to be in the order of gas–liquid velocity difference divided by the gas vorticity layer thickness (
![]() $\unicode[STIX]{x1D6FF}_{g}$
), i.e.
$\unicode[STIX]{x1D6FF}_{g}$
), i.e.
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}=(U_{l}-U_{g})/\unicode[STIX]{x1D6FF}_{g}$
; where
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}=(U_{l}-U_{g})/\unicode[STIX]{x1D6FF}_{g}$
; where
![]() $\unicode[STIX]{x1D6FF}_{g}$
varies between
$\unicode[STIX]{x1D6FF}_{g}$
varies between
![]() $45$
to
$45$
to
![]() $50~\unicode[STIX]{x03BC}\text{m}$
. In our analysis,
$50~\unicode[STIX]{x03BC}\text{m}$
. In our analysis,
![]() $\unicode[STIX]{x1D6FF}_{g}=D/4=50~\unicode[STIX]{x03BC}\text{m}$
is chosen for all three cases. With this value, the maximum azimuthal vorticity is
$\unicode[STIX]{x1D6FF}_{g}=D/4=50~\unicode[STIX]{x03BC}\text{m}$
is chosen for all three cases. With this value, the maximum azimuthal vorticity is
![]() $9\times 10^{5}$
,
$9\times 10^{5}$
,
![]() $8\times 10^{5}$
and
$8\times 10^{5}$
and
![]() $5\times 10^{5}~\text{s}^{-1}$
for cases 1, 2 and 3, respectively. These theoretical values are consistent with the measured
$5\times 10^{5}~\text{s}^{-1}$
for cases 1, 2 and 3, respectively. These theoretical values are consistent with the measured
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
at the beginning of the simulations. Figure 23(c) shows that
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
at the beginning of the simulations. Figure 23(c) shows that
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
is very close to 1.0 for all three cases at early times.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
is very close to 1.0 for all three cases at early times.
In all cases, as the wave travels downstream,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
decreases with time (figure 23
c); however, the rate of this fall is higher at lower
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
decreases with time (figure 23
c); however, the rate of this fall is higher at lower
![]() $\hat{U}$
(case 1). By the time the wave reaches the BCR (at about
$\hat{U}$
(case 1). By the time the wave reaches the BCR (at about
![]() $t^{\ast }=8$
), the instantaneous mean
$t^{\ast }=8$
), the instantaneous mean
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
is about 30 % of its initial value in case 1, and about 55 % of its initial value in case 3. One main reason for this difference is the higher and faster spreading and diffusion of the vorticity at lower
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
is about 30 % of its initial value in case 1, and about 55 % of its initial value in case 3. One main reason for this difference is the higher and faster spreading and diffusion of the vorticity at lower
![]() $\hat{U}$
, as will be shown later in this section. Since the outward growth of the instabilities is higher at lower
$\hat{U}$
, as will be shown later in this section. Since the outward growth of the instabilities is higher at lower
![]() $\hat{U}$
,
$\hat{U}$
,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
is less concentrated near the surface compared to the higher
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
is less concentrated near the surface compared to the higher
![]() $\hat{U}$
case. This higher spread rate decreases the average
$\hat{U}$
case. This higher spread rate decreases the average
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
per unit volume. More importantly, the faster growth of the vorticity layer thickness at higher
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
per unit volume. More importantly, the faster growth of the vorticity layer thickness at higher
![]() $U_{r}$
results in the faster drop of
$U_{r}$
results in the faster drop of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
in time, as will be discussed in details in § 3.6.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
in time, as will be discussed in details in § 3.6.
The fall in the value of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
accompanies higher growth rates of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
accompanies higher growth rates of
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{r}$
. Figure 23(a,b) shows that both
$\unicode[STIX]{x1D714}_{r}$
. Figure 23(a,b) shows that both
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{r}$
have a higher growth rate at lower
$\unicode[STIX]{x1D714}_{r}$
have a higher growth rate at lower
![]() $\hat{U}$
. This increase in the magnitude of the axial and radial vorticity components continues until the wave comes very close to the BCR, at about
$\hat{U}$
. This increase in the magnitude of the axial and radial vorticity components continues until the wave comes very close to the BCR, at about
![]() $t^{\ast }=8{-}9$
. Henceforth, the wave gets influenced by the vortices in the recirculation zone and both
$t^{\ast }=8{-}9$
. Henceforth, the wave gets influenced by the vortices in the recirculation zone and both
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{r}$
drop. The tracking of the vorticity components near the wave surface is stopped when the wave enters the jet cap. The higher growth rate of
$\unicode[STIX]{x1D714}_{r}$
drop. The tracking of the vorticity components near the wave surface is stopped when the wave enters the jet cap. The higher growth rate of
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{r}$
at low
$\unicode[STIX]{x1D714}_{r}$
at low
![]() $\hat{U}$
results in higher streamwise stretching of the waves and higher radial growth of the waves amplitude, evident in figure 9.
$\hat{U}$
results in higher streamwise stretching of the waves and higher radial growth of the waves amplitude, evident in figure 9.

Figure 24. Kinematic variation of
![]() $\unicode[STIX]{x1D714}_{x}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
for different velocity ratios.
$\unicode[STIX]{x1D714}_{x}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
for different velocity ratios.
To better illustrate the influence of
![]() $\hat{U}$
on the growth of streamwise instabilities, figure 24 shows the ratio of streamwise to azimuthal vorticities (
$\hat{U}$
on the growth of streamwise instabilities, figure 24 shows the ratio of streamwise to azimuthal vorticities (
![]() $\unicode[STIX]{x1D714}_{x}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) in time. As described above, the relative order of magnitude of
$\unicode[STIX]{x1D714}_{x}/\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) in time. As described above, the relative order of magnitude of
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
is the best indicator of the deviation of jet instability from axisymmetry. As expected,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
is the best indicator of the deviation of jet instability from axisymmetry. As expected,
![]() $\unicode[STIX]{x1D714}_{x}$
soon becomes 0.7 times the magnitude of
$\unicode[STIX]{x1D714}_{x}$
soon becomes 0.7 times the magnitude of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
at
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
at
![]() $\hat{U}=0.1$
, which demonstrates itself as highly asymmetric surface instabilities with many lobes and ligaments in case 1 (see figure 9
a). In case 3, on the other hand,
$\hat{U}=0.1$
, which demonstrates itself as highly asymmetric surface instabilities with many lobes and ligaments in case 1 (see figure 9
a). In case 3, on the other hand,
![]() $\unicode[STIX]{x1D714}_{x}$
is still an order of magnitude smaller than
$\unicode[STIX]{x1D714}_{x}$
is still an order of magnitude smaller than
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(
![]() $\unicode[STIX]{x1D714}_{x}=0.2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) even at a much later time,
$\unicode[STIX]{x1D714}_{x}=0.2\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) even at a much later time,
![]() $t^{\ast }>11$
. Following this significant difference in the magnitude of vorticities, the liquid surface remains fairly axisymmetric for a large portion and the asymmetric instabilities only emerge very close to the cap (see figure 9
c).
$t^{\ast }>11$
. Following this significant difference in the magnitude of vorticities, the liquid surface remains fairly axisymmetric for a large portion and the asymmetric instabilities only emerge very close to the cap (see figure 9
c).
In the spatial analysis, the vorticity components are measured versus axial distance from the inlet plane. In this approach, a snapshot is taken from the liquid jet at the end of the simulations (
![]() ${\approx}t^{\ast }=11.5$
) and the vorticity components are averaged at each surface wave. In this calculation, an annular control volume with thickness (in the axial direction) and height (in the radial direction) equal to the KH wavelength (
${\approx}t^{\ast }=11.5$
) and the vorticity components are averaged at each surface wave. In this calculation, an annular control volume with thickness (in the axial direction) and height (in the radial direction) equal to the KH wavelength (
![]() $\unicode[STIX]{x1D706}_{KH}$
) is considered around each KH wave, as shown in figure 25. The absolute value of each vorticity component is integrated in each control volume and divided by its volume to obtain the volumetric average. The mean values of
$\unicode[STIX]{x1D706}_{KH}$
) is considered around each KH wave, as shown in figure 25. The absolute value of each vorticity component is integrated in each control volume and divided by its volume to obtain the volumetric average. The mean values of
![]() $\unicode[STIX]{x1D714}$
along the axis are shown in figures 26 and 27 for cases 1 and 3, respectively.
$\unicode[STIX]{x1D714}$
along the axis are shown in figures 26 and 27 for cases 1 and 3, respectively.

Figure 25. Identification of the control volumes used for calculation of vorticity components per KH wavelength.
To compare the spatial results with those obtained from the kinematic analysis, the kinematic results of figure 23 are assumed to convect with the wave speed (Dimotakis speed,
![]() $U_{D}$
) in each case to obtain the axial distance of the corresponding wave from the inlet plane. Therefore, both results are now comparable; see figures 26 and 27.
$U_{D}$
) in each case to obtain the axial distance of the corresponding wave from the inlet plane. Therefore, both results are now comparable; see figures 26 and 27.
Figure 26. Comparison of the spatial and kinematic calculations of
![]() $\unicode[STIX]{x1D714}_{x}$
(a); and
$\unicode[STIX]{x1D714}_{x}$
(a); and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(b) in case 1 (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(b) in case 1 (
![]() $\hat{U}=0.1$
).
$\hat{U}=0.1$
).
Figure 27. Comparison of the spatial and kinematic calculations of
![]() $\unicode[STIX]{x1D714}_{x}$
(a); and
$\unicode[STIX]{x1D714}_{x}$
(a); and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(b) in case 3 (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(b) in case 3 (
![]() $\hat{U}=0.5$
).
$\hat{U}=0.5$
).
In both cases, the spatial and kinematic measurements of
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
match well for a few diameters downstream of the nozzle exit; i.e. before
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
match well for a few diameters downstream of the nozzle exit; i.e. before
![]() $x/D=6.25$
in case 1 (figure 26), and before
$x/D=6.25$
in case 1 (figure 26), and before
![]() $x/D=5.75$
in case 3 (figure 27). Farther downstream, however, the two calculations diverge. The two regions are demarcated with broken red lines on the plots. Since the results to the left of this red line match very well, it is concluded that those vorticity developments are periodic. This conclusion originates from the fact that the same order of vorticity magnitude is obtained for all consecutive waves formed on the jet stem (as represented by the spatial data) compared to the magnitude of the vorticity on a single wave convecting downstream (as followed by the kinematic data). To the right of the red line, this periodicity fades away and the two results take completely separate paths. This region is denoted as ‘non-periodic’ on the plots. Since the spatial and kinematic results differ in this region, the pattern of the vorticity growth (decay) rate varies from wave to wave. Therefore, each wave experiences a different vortex development in time and in space which is totally different from what the following waves will experience, i.e. a non-periodic pattern.
$x/D=5.75$
in case 3 (figure 27). Farther downstream, however, the two calculations diverge. The two regions are demarcated with broken red lines on the plots. Since the results to the left of this red line match very well, it is concluded that those vorticity developments are periodic. This conclusion originates from the fact that the same order of vorticity magnitude is obtained for all consecutive waves formed on the jet stem (as represented by the spatial data) compared to the magnitude of the vorticity on a single wave convecting downstream (as followed by the kinematic data). To the right of the red line, this periodicity fades away and the two results take completely separate paths. This region is denoted as ‘non-periodic’ on the plots. Since the spatial and kinematic results differ in this region, the pattern of the vorticity growth (decay) rate varies from wave to wave. Therefore, each wave experiences a different vortex development in time and in space which is totally different from what the following waves will experience, i.e. a non-periodic pattern.

Figure 28. The liquid jet snapshots at
![]() $t^{\ast }=10.0$
on a slice cutting through
$t^{\ast }=10.0$
on a slice cutting through
![]() $y=0$
; case 1 (a), and case 3 (b).
$y=0$
; case 1 (a), and case 3 (b).
Having a closer look at the snapshot, from which the spatial data were derived – shown in figure 28 – it is seen that the red lines separating the periodic and the non-periodic regions lie very close to where the UR and the BCR separate. In particular, these red lines separate the UR regions of the jet – where the vortices are independent – from where the vortices are affected by the vortices shed from the BCR. Figure 28 clearly shows that the vortices to the right of the red line are under the influence (mutual induction) of the vortices in the recirculation zone. That is in fact why the vortex development in that range is non-periodic. On the contrary, the KH vortices in the periodic zone seem to follow the same growth and deformation in time and space.
The kinematic tracking in the spatially developing flow qualitatively represents the type of behaviour found in a temporal study. The results presented in this section clearly validate the temporal studies conducted by JS, Jarrahbashi et al. (Reference Jarrahbashi, Sirignano, Popov and Hussain2016), ZSH1 and ZSH2, and demonstrate that the UR on the stem of the jet can be studied very well in a temporal analysis on a liquid segment with periodic boundary conditions. Clearly, the UR grows in time and takes a larger portion of the liquid jet in long time. The BCR also grows, as the vortices shed in the BCR convect upstream and increase their influence on the UR waves close to the indentation; however, the growth of the UR is much greater than that of the BCR. Therefore, the UR vortex dynamics and surface deformation dominate the atomization process at long time when the stem gets longer. In particular, the temporal studies are more effective at higher
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
ranges (like case 1), where the waves deform faster and completely break up before reaching the BCR.
$We_{r}$
ranges (like case 1), where the waves deform faster and completely break up before reaching the BCR.
Note in figure 28 that the waves grow much faster and are stretched radially outward at low
![]() $\hat{U}$
(case 1). This is consistent with the higher growth rate in
$\hat{U}$
(case 1). This is consistent with the higher growth rate in
![]() $\unicode[STIX]{x1D714}_{r}$
for case 1 compared to case 3, shown in figure 23(b). Also, the
$\unicode[STIX]{x1D714}_{r}$
for case 1 compared to case 3, shown in figure 23(b). Also, the
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
contours are more widely distributed in case 1 compared to case 3, which confirms our earlier reasoning for the faster decay in the magnitude of mean
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
contours are more widely distributed in case 1 compared to case 3, which confirms our earlier reasoning for the faster decay in the magnitude of mean
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
with time, in case 1.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
with time, in case 1.
3.5 Streamwise vorticity generation
The streamwise (axial) vorticity,
![]() $\unicode[STIX]{x1D714}_{x}$
, is crucial in the initiation of the 3-D instability on liquid jets (Yecko & Zaleski Reference Yecko and Zaleski2005). The
$\unicode[STIX]{x1D714}_{x}$
, is crucial in the initiation of the 3-D instability on liquid jets (Yecko & Zaleski Reference Yecko and Zaleski2005). The
![]() $\unicode[STIX]{x1D714}_{x}$
generation via vortex stretching and vortex tilting – i.e. strain-vorticity interactions – and baroclinic effects are analysed and compared in this section for cases 1–3 to show the effects of
$\unicode[STIX]{x1D714}_{x}$
generation via vortex stretching and vortex tilting – i.e. strain-vorticity interactions – and baroclinic effects are analysed and compared in this section for cases 1–3 to show the effects of
![]() $\hat{U}$
on these contributing factors. Therefore, the generation of the 3-D deformations on the liquid-jet interface is specifically addressed here. JS performed a similar analysis for the round jets (in quiescent gas) at a wide range of density ratios, and showed that at low
$\hat{U}$
on these contributing factors. Therefore, the generation of the 3-D deformations on the liquid-jet interface is specifically addressed here. JS performed a similar analysis for the round jets (in quiescent gas) at a wide range of density ratios, and showed that at low
![]() $\hat{\unicode[STIX]{x1D70C}}$
, of
$\hat{\unicode[STIX]{x1D70C}}$
, of
![]() $O(10^{-2})$
, the baroclinic effect, i.e. the Rayleigh–Taylor instability, is the dominant cause of the initiation of 3-D structures. This is consistent with the suggestion of Marmottant & Villermaux (Reference Marmottant and Villermaux2004) who performed experiments at lower pressures and gas density. However, for a higher
$O(10^{-2})$
, the baroclinic effect, i.e. the Rayleigh–Taylor instability, is the dominant cause of the initiation of 3-D structures. This is consistent with the suggestion of Marmottant & Villermaux (Reference Marmottant and Villermaux2004) who performed experiments at lower pressures and gas density. However, for a higher
![]() $\hat{\unicode[STIX]{x1D70C}}$
of
$\hat{\unicode[STIX]{x1D70C}}$
of
![]() $O(10^{-1})$
or greater, JS showed that the azimuthal tilting and radial tilting of the vortex rings are the dominant effects in streamwise vorticity generation. Similar results were obtained by ZSH2 for planar jets. However, they showed that the vortex tilting terms, even though highest in magnitude, are not the most dominant cause of
$O(10^{-1})$
or greater, JS showed that the azimuthal tilting and radial tilting of the vortex rings are the dominant effects in streamwise vorticity generation. Similar results were obtained by ZSH2 for planar jets. However, they showed that the vortex tilting terms, even though highest in magnitude, are not the most dominant cause of
![]() $\unicode[STIX]{x1D714}_{x}$
generation since they nearly cancel each other. None of those studies analysed the effects of gas-to-liquid velocity ratio on the vortex generation. This is covered here.
$\unicode[STIX]{x1D714}_{x}$
generation since they nearly cancel each other. None of those studies analysed the effects of gas-to-liquid velocity ratio on the vortex generation. This is covered here.
The complete form of the vorticity equation is
where
![]() $\boldsymbol{u}$
and
$\boldsymbol{u}$
and
![]() $\unicode[STIX]{x1D74E}$
are the velocity and vorticity vectors, respectively.
$\unicode[STIX]{x1D74E}$
are the velocity and vorticity vectors, respectively.
![]() $\unicode[STIX]{x1D749}$
is the viscous stress tensor, and
$\unicode[STIX]{x1D749}$
is the viscous stress tensor, and
![]() $\boldsymbol{F}_{\unicode[STIX]{x1D748}}$
is the surface tension force. Since the fluids are incompressible, the second term on the right-hand side is zero. A simple dimensional analysis shows that the viscous diffusion term (the third term on the right-hand side) scales as
$\boldsymbol{F}_{\unicode[STIX]{x1D748}}$
is the surface tension force. Since the fluids are incompressible, the second term on the right-hand side is zero. A simple dimensional analysis shows that the viscous diffusion term (the third term on the right-hand side) scales as
![]() $\unicode[STIX]{x1D707}U_{r}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}_{g}^{3}$
, which for a typical case considered in our study, e.g.
$\unicode[STIX]{x1D707}U_{r}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6FF}_{g}^{3}$
, which for a typical case considered in our study, e.g.
![]() $\unicode[STIX]{x1D707}=O(10^{-3})~\text{Pa}~\text{s}$
,
$\unicode[STIX]{x1D707}=O(10^{-3})~\text{Pa}~\text{s}$
,
![]() $U_{r}=O(10)~\text{m}~\text{s}^{-1}$
,
$U_{r}=O(10)~\text{m}~\text{s}^{-1}$
,
![]() $\unicode[STIX]{x1D70C}=O(10^{3})~\text{kg}~\text{m}^{-3}$
and a gas vorticity layer thickness of
$\unicode[STIX]{x1D70C}=O(10^{3})~\text{kg}~\text{m}^{-3}$
and a gas vorticity layer thickness of
![]() $\unicode[STIX]{x1D6FF}_{g}=50~\unicode[STIX]{x03BC}\text{m}$
, gives a magnitude of
$\unicode[STIX]{x1D6FF}_{g}=50~\unicode[STIX]{x03BC}\text{m}$
, gives a magnitude of
![]() ${\approx}O(10^{9})~\text{s}^{-2}$
. The surface tension term (the last term) scales as
${\approx}O(10^{9})~\text{s}^{-2}$
. The surface tension term (the last term) scales as
![]() $\unicode[STIX]{x1D70E}\unicode[STIX]{x1D705}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6E5}^{2}$
; which for a typical case with
$\unicode[STIX]{x1D70E}\unicode[STIX]{x1D705}/\unicode[STIX]{x1D70C}\unicode[STIX]{x1D6E5}^{2}$
; which for a typical case with
![]() $\unicode[STIX]{x1D70E}=O(10^{-2})~\text{N}~\text{m}^{-1}$
, and a radius of curvature of
$\unicode[STIX]{x1D70E}=O(10^{-2})~\text{N}~\text{m}^{-1}$
, and a radius of curvature of
![]() $100~\unicode[STIX]{x03BC}\text{m}$
(
$100~\unicode[STIX]{x03BC}\text{m}$
(
![]() $\unicode[STIX]{x1D705}=10^{4}~\text{m}^{-1}$
) and mesh size of
$\unicode[STIX]{x1D705}=10^{4}~\text{m}^{-1}$
) and mesh size of
![]() $\unicode[STIX]{x1D6E5}=2~\unicode[STIX]{x03BC}\text{m}$
, gives a result in the order of
$\unicode[STIX]{x1D6E5}=2~\unicode[STIX]{x03BC}\text{m}$
, gives a result in the order of
![]() $10^{10}~\text{s}^{-2}$
. As will be shown in this section, these two terms are two orders of magnitude smaller than the other terms in (3.5), and therefore have a negligible contribution to vorticity generation (although viscosity and surface tension do have consequence elsewhere in our analysis). Therefore, the rate of change of
$10^{10}~\text{s}^{-2}$
. As will be shown in this section, these two terms are two orders of magnitude smaller than the other terms in (3.5), and therefore have a negligible contribution to vorticity generation (although viscosity and surface tension do have consequence elsewhere in our analysis). Therefore, the rate of change of
![]() $\unicode[STIX]{x1D714}_{x}$
is approximately
$\unicode[STIX]{x1D714}_{x}$
is approximately
where
![]() $\unicode[STIX]{x1D714}_{x}$
,
$\unicode[STIX]{x1D714}_{x}$
,
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
,
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
,
![]() $\unicode[STIX]{x1D714}_{r}$
and
$\unicode[STIX]{x1D714}_{r}$
and
![]() $u$
denote the streamwise, azimuthal, and radial vorticity, and streamwise velocity, respectively. The terms on the right-hand side denote:
$u$
denote the streamwise, azimuthal, and radial vorticity, and streamwise velocity, respectively. The terms on the right-hand side denote:
(1) Streamwise vortex stretching,
 $\unicode[STIX]{x1D714}_{x}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)$
.
$\unicode[STIX]{x1D714}_{x}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}x)$
.(2) Azimuthal vortex tilting,
 $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/r\unicode[STIX]{x2202}\unicode[STIX]{x1D703})$
.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}(\unicode[STIX]{x2202}u/r\unicode[STIX]{x2202}\unicode[STIX]{x1D703})$
.(3) Radial vortex tilting,
 $\unicode[STIX]{x1D714}_{r}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}r)$
.
$\unicode[STIX]{x1D714}_{r}(\unicode[STIX]{x2202}u/\unicode[STIX]{x2202}r)$
.(4) Baroclinic vorticity generation,
 $(1/r\unicode[STIX]{x1D70C}^{2})[(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r)(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})-(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r)]$
.
$(1/r\unicode[STIX]{x1D70C}^{2})[(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r)(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})-(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r)]$
.
Density gradient is normal to the liquid interface, i.e. approximately in the
![]() $r$
direction. Near the inlet plane, the azimuthal density gradient, i.e.
$r$
direction. Near the inlet plane, the azimuthal density gradient, i.e.
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
, is negligible compared to
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703}$
, is negligible compared to
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r$
since the jet cross-section is nearly circular with slight perturbations. Yet, this term accounts for the baroclinic effect, which can deform the interface in the azimuthal direction. In our data analysis, the gradients have been calculated in the entire computational domain. The volumetric average of each term is then calculated by integrating the term in the control volumes surrounding each KH wave, as shown in figure 25.
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r$
since the jet cross-section is nearly circular with slight perturbations. Yet, this term accounts for the baroclinic effect, which can deform the interface in the azimuthal direction. In our data analysis, the gradients have been calculated in the entire computational domain. The volumetric average of each term is then calculated by integrating the term in the control volumes surrounding each KH wave, as shown in figure 25.
Figure 29 shows the contribution of the four above-mentioned terms to
![]() $\unicode[STIX]{x1D714}_{x}$
generation for cases 1–3. In all cases, the azimuthal and radial vortex tilting toward the axial direction are the largest. However, as shown in figure 30, these two terms are nearly identical in magnitude but with opposite signs. Any radial filament will be tilted by the radial velocity gradient and aligned axially (figure 31
a), but if this is a leg of a hairpin then self-induction by the other leg will also align it axially (figure 31
b) – except that these two axially aligned filaments will have opposite signs, hence balancing each other. The self-induction of the legs becomes stronger radially outward, where the legs are closer to each other near the hairpin tip. This causes a clockwise tilting of the legs and turns the hairpin downstream. The self-induction of the far leg is denoted by black arrows and the self-induction of the near leg is denoted by white arrows in figure 31(b). Therefore, these two tilting terms, even though each separately the largest, are not the most dominant effect in
$\unicode[STIX]{x1D714}_{x}$
generation for cases 1–3. In all cases, the azimuthal and radial vortex tilting toward the axial direction are the largest. However, as shown in figure 30, these two terms are nearly identical in magnitude but with opposite signs. Any radial filament will be tilted by the radial velocity gradient and aligned axially (figure 31
a), but if this is a leg of a hairpin then self-induction by the other leg will also align it axially (figure 31
b) – except that these two axially aligned filaments will have opposite signs, hence balancing each other. The self-induction of the legs becomes stronger radially outward, where the legs are closer to each other near the hairpin tip. This causes a clockwise tilting of the legs and turns the hairpin downstream. The self-induction of the far leg is denoted by black arrows and the self-induction of the near leg is denoted by white arrows in figure 31(b). Therefore, these two tilting terms, even though each separately the largest, are not the most dominant effect in
![]() $\unicode[STIX]{x1D714}_{x}$
generation. This was also qualitatively shown by ZSH2 for liquid sheets. The growth rate of the vortex tilting terms, however, is smaller compared to both baroclinicity and streamwise stretching. The vortex tilting terms grow about one order of magnitude from the inlet plane to the BCR plane, whereas the baroclinicity increases by about three orders of magnitude, and the streamwise stretching, has the highest growth rate with more than three orders of magnitude growth on average. By the end of the lifespan of the KH waves, all four effects have comparable magnitudes.
$\unicode[STIX]{x1D714}_{x}$
generation. This was also qualitatively shown by ZSH2 for liquid sheets. The growth rate of the vortex tilting terms, however, is smaller compared to both baroclinicity and streamwise stretching. The vortex tilting terms grow about one order of magnitude from the inlet plane to the BCR plane, whereas the baroclinicity increases by about three orders of magnitude, and the streamwise stretching, has the highest growth rate with more than three orders of magnitude growth on average. By the end of the lifespan of the KH waves, all four effects have comparable magnitudes.
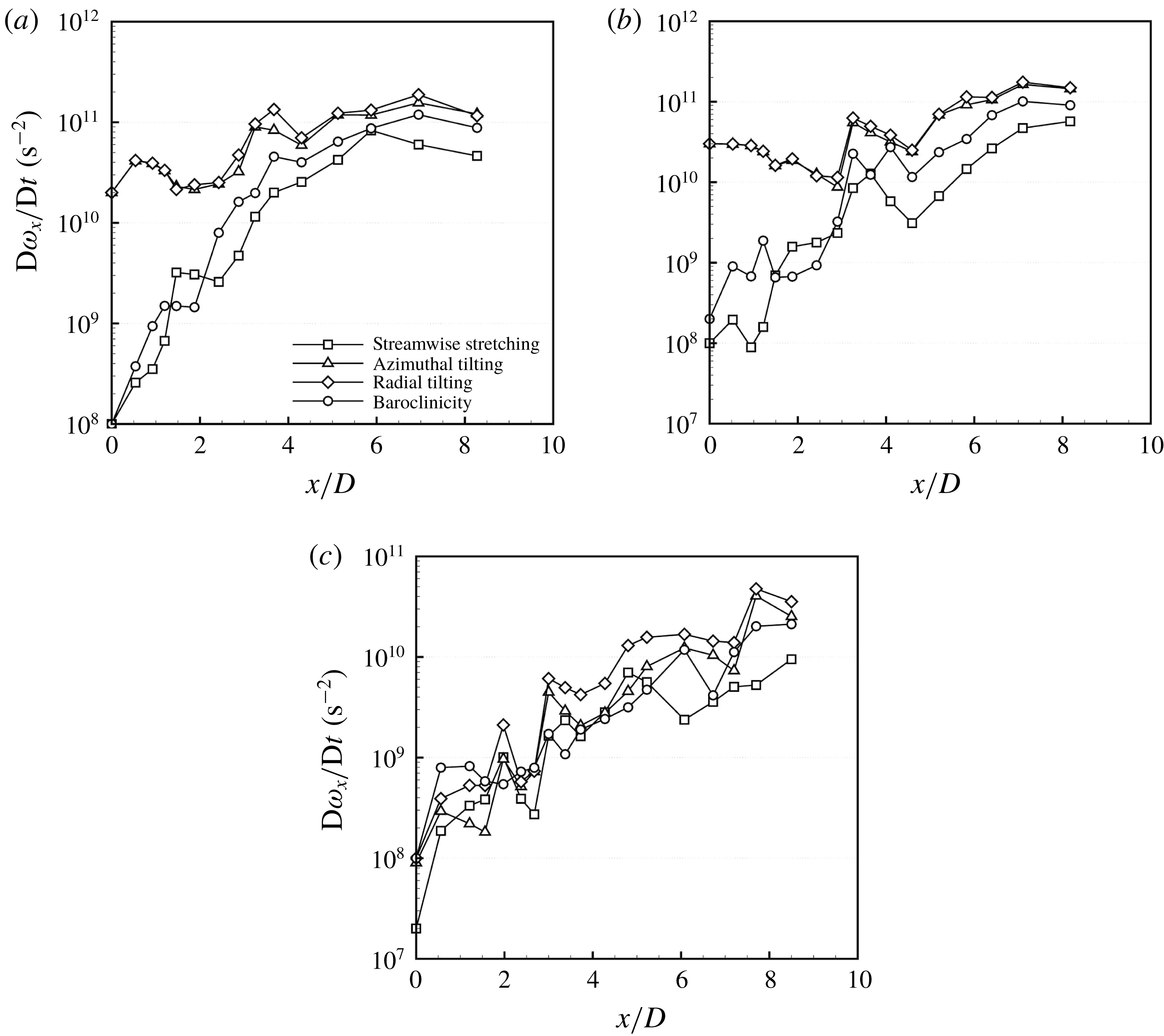
Figure 29. Contributions of streamwise vortex stretching (squares), azimuthal vortex tilting (triangles), radial vortex tilting (diamonds), and baroclinicity (circles) to the generation of
![]() $\unicode[STIX]{x1D714}_{x}$
at the liquid surface for case 1 (a) case 2 (b) and case 3 (c);
$\unicode[STIX]{x1D714}_{x}$
at the liquid surface for case 1 (a) case 2 (b) and case 3 (c);
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.

Figure 30. Comparison between the azimuthal and radial vortex tilting terms at the liquid surface for case 1;
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.
In all three cases, the baroclinic vorticity generation is larger than the streamwise vortex stretching. The differences between the four terms become more evident at lower
![]() $\hat{U}$
(case 1). At higher
$\hat{U}$
(case 1). At higher
![]() $\hat{U}$
, on the other hand, the competition between the four terms is very close, and the four trends are almost indistinguishable (figure 29
c). Figure 29 indicates that (at the same density ratio) baroclinicity becomes larger as
$\hat{U}$
, on the other hand, the competition between the four terms is very close, and the four trends are almost indistinguishable (figure 29
c). Figure 29 indicates that (at the same density ratio) baroclinicity becomes larger as
![]() $\hat{U}$
decreases. At
$\hat{U}$
decreases. At
![]() $x/D\approx 8.5$
, the mean baroclinicity is almost
$x/D\approx 8.5$
, the mean baroclinicity is almost
![]() $10^{11}~\text{s}^{-2}$
for case 1, but at the same axial distance it decreases to
$10^{11}~\text{s}^{-2}$
for case 1, but at the same axial distance it decreases to
![]() $2\times 10^{10}~\text{s}^{-2}$
in case 3. Since all three terms have the same density ratio and only differ in velocity difference, it is necessary to explain this difference in baroclinicity between cases 1 and 3, where velocity gradient does not explicitly appear in the calculations.
$2\times 10^{10}~\text{s}^{-2}$
in case 3. Since all three terms have the same density ratio and only differ in velocity difference, it is necessary to explain this difference in baroclinicity between cases 1 and 3, where velocity gradient does not explicitly appear in the calculations.
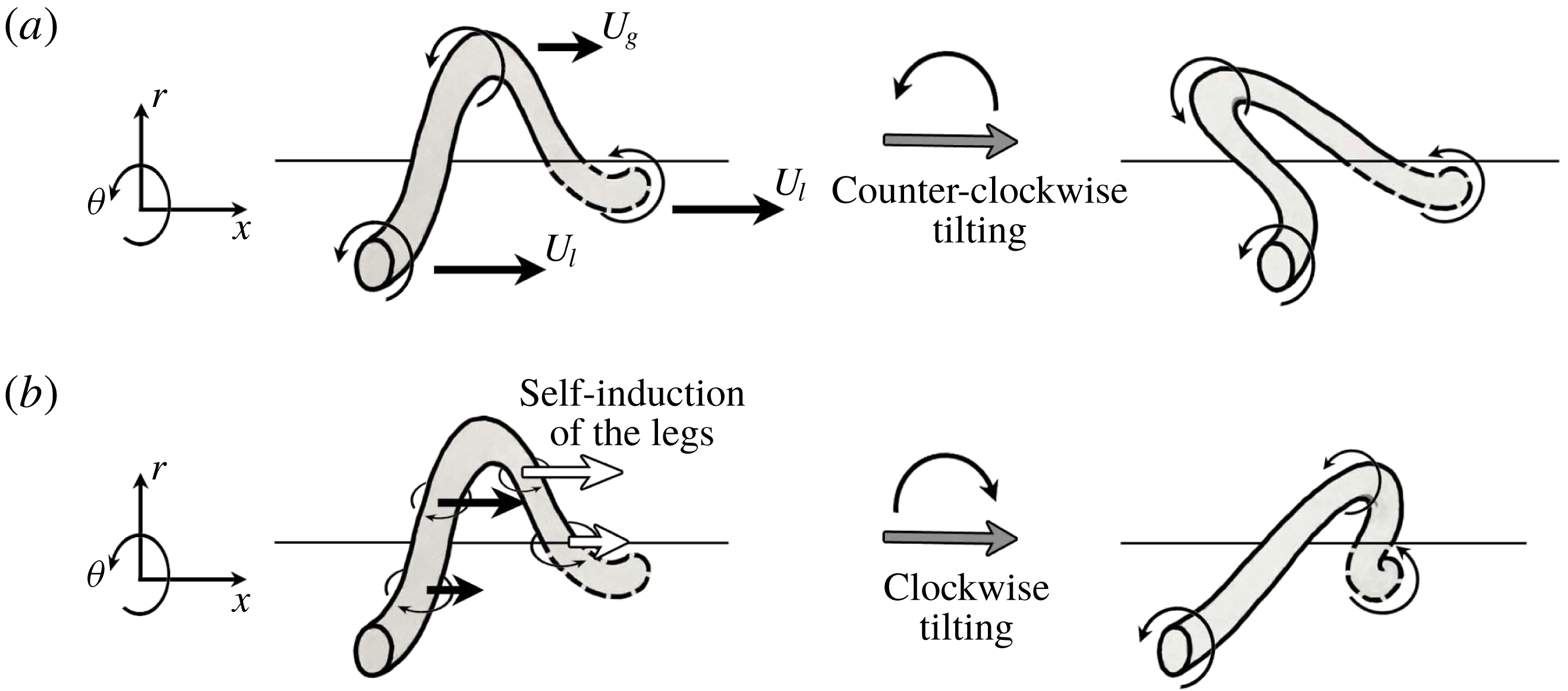
Figure 31. Opposite tilting effects: (a) upstream tilting of a transverse hairpin by the mean shear; (b) downstream tilting of a transverse hairpin by the hairpin’s self-induction.
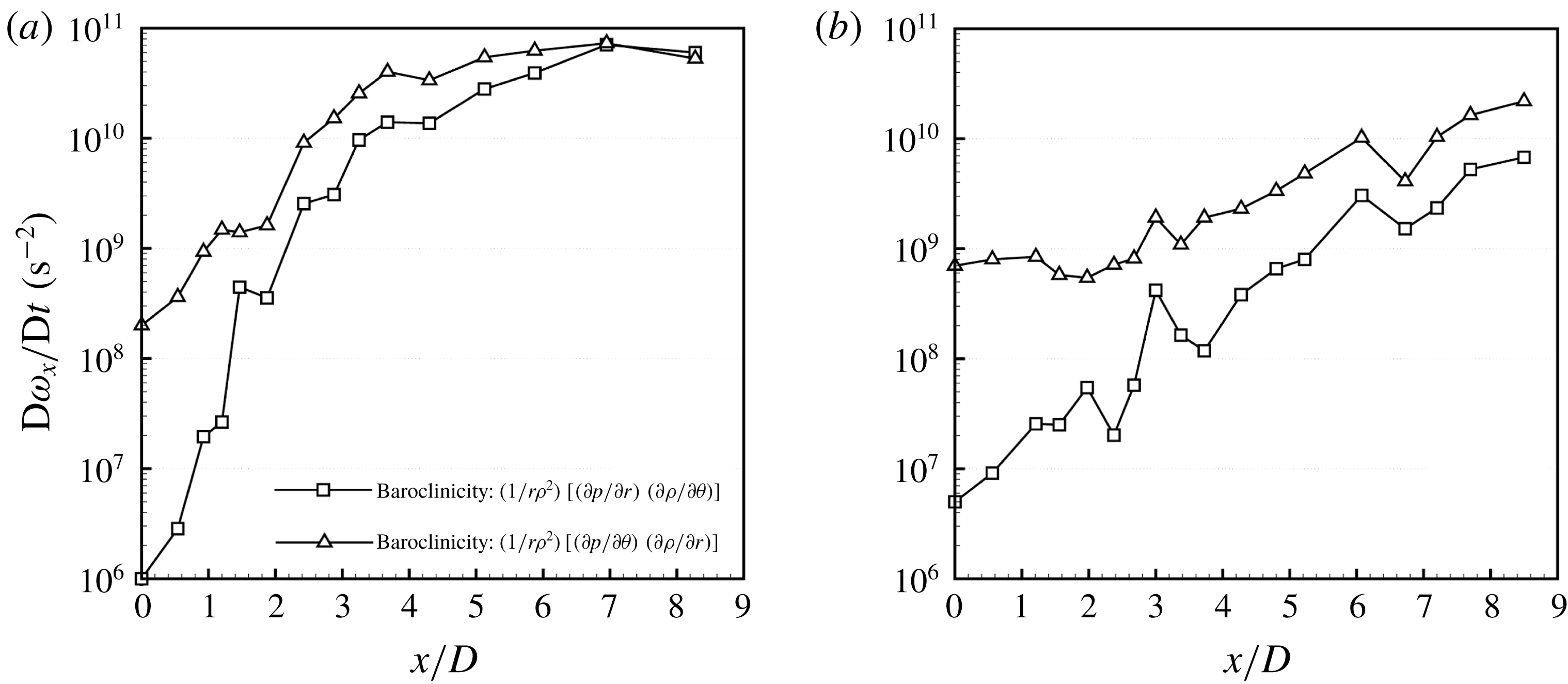
Figure 32. Comparison between the radial and azimuthal pressure gradient terms of baroclinicity in case 1 (a) and case 3 (b),
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.
To explain the difference between the baroclinicity in cases 1 and 3, the two contributing parts of baroclinicity – i.e. radial pressure gradient,
![]() $(1/r\unicode[STIX]{x1D70C}^{2})[(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r)(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})]$
, and azimuthal pressure gradient,
$(1/r\unicode[STIX]{x1D70C}^{2})[(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r)(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})]$
, and azimuthal pressure gradient,
![]() $(1/r\unicode[STIX]{x1D70C}^{2})[(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r)]$
– are compared in figures 32(a,b) for cases 1 and 3, respectively. Even though both terms are slightly larger in case 3 compared to case 1 near the inlet plane, the growth rates of both terms are higher in case 1, and both terms become almost an order of magnitude larger than in case 3 at large downstream distances (
$(1/r\unicode[STIX]{x1D70C}^{2})[(\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}\unicode[STIX]{x1D703})(\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r)]$
– are compared in figures 32(a,b) for cases 1 and 3, respectively. Even though both terms are slightly larger in case 3 compared to case 1 near the inlet plane, the growth rates of both terms are higher in case 1, and both terms become almost an order of magnitude larger than in case 3 at large downstream distances (
![]() $x/D>8$
). In both cases, the azimuthal pressure gradient term is dominant compared to the radial pressure gradient term at early times and close to the nozzle exit; however, farther downstream, the radial pressure gradient (azimuthal density gradient) term, which has a higher growth rate, gets to a comparable scale, especially at lower
$x/D>8$
). In both cases, the azimuthal pressure gradient term is dominant compared to the radial pressure gradient term at early times and close to the nozzle exit; however, farther downstream, the radial pressure gradient (azimuthal density gradient) term, which has a higher growth rate, gets to a comparable scale, especially at lower
![]() $\hat{U}$
(case 1). Clearly, a larger contributor to this effect is the density gradient rather than the pressure gradient, because the radial density gradient would remain nearly constant along the axis, but the azimuthal density gradient grows significantly due to the azimuthal surface deformation and lobe formations that develop farther downstream. To specifically show the dominant effects of pressure and density gradient on the baroclinic vorticity reinforcement near the upstream and downstream ranges, the magnitude of pressure and density gradients are shown in figure 33.
$\hat{U}$
(case 1). Clearly, a larger contributor to this effect is the density gradient rather than the pressure gradient, because the radial density gradient would remain nearly constant along the axis, but the azimuthal density gradient grows significantly due to the azimuthal surface deformation and lobe formations that develop farther downstream. To specifically show the dominant effects of pressure and density gradient on the baroclinic vorticity reinforcement near the upstream and downstream ranges, the magnitude of pressure and density gradients are shown in figure 33.
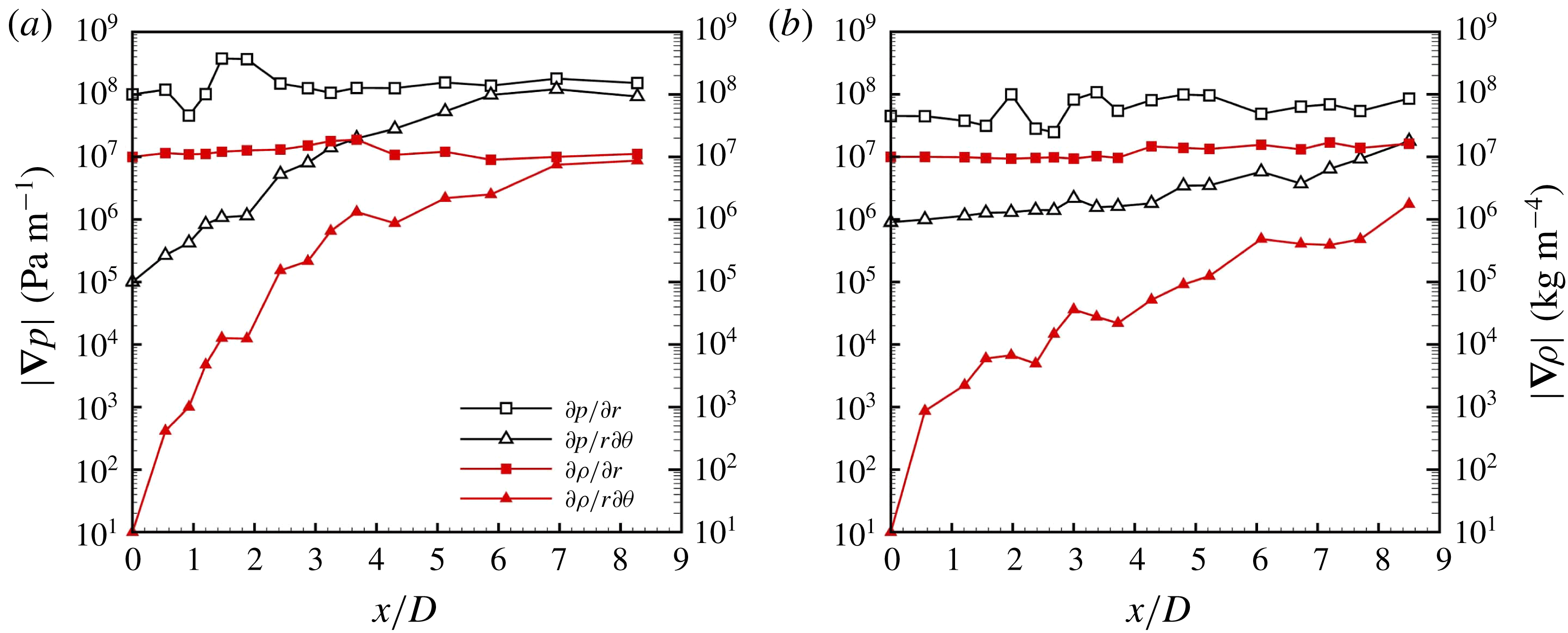
Figure 33. Comparison between the radial and azimuthal pressure gradients and density gradients in case 1 (a) and case 3 (b),
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.
As mentioned before, and now quantitatively validated, both pressure and density gradients in the radial direction remain nearly constant along the axis in both cases, whereas the azimuthal gradients grow in time and also in
![]() $x$
. The growth of azimuthal gradients is expected as 3-D instabilities occur on the liquid surface. In both cases, the radial gradients are larger than the azimuthal gradients for both pressure and density in the upstream range. Further downstream (
$x$
. The growth of azimuthal gradients is expected as 3-D instabilities occur on the liquid surface. In both cases, the radial gradients are larger than the azimuthal gradients for both pressure and density in the upstream range. Further downstream (
![]() $x/D>7$
), however, the azimuthal and radial pressure and density gradients become comparable in case 1, but still are an order of magnitude apart in case 3. More importantly, the azimuthal density gradient is nearly one order of magnitude larger in case 1 (
$x/D>7$
), however, the azimuthal and radial pressure and density gradients become comparable in case 1, but still are an order of magnitude apart in case 3. More importantly, the azimuthal density gradient is nearly one order of magnitude larger in case 1 (
![]() $\hat{U}=0.1$
) than in case 3 (
$\hat{U}=0.1$
) than in case 3 (
![]() $\hat{U}=0.5$
). This indicates more azimuthal instabilities and surface deformations at lower velocity ratios, which is consistent with the higher number of lobes in case 1 than in case 3, as was observed in figure 9.
$\hat{U}=0.5$
). This indicates more azimuthal instabilities and surface deformations at lower velocity ratios, which is consistent with the higher number of lobes in case 1 than in case 3, as was observed in figure 9.
3.6 Vortex and pressure forces in instability development
Our analysis is extended to a more detailed quantification of the pressure and inertia forces in the momentum equation to better illustrate the sources of vorticity and pressure gradients and to explain the differences caused by the velocity ratio. In this regard, the non-conservative form of the momentum equation for an incompressible flow is used,
where
![]() $V$
is the velocity magnitude. In this form, the convective acceleration is broken into two parts – one due to the kinetic energy gradient, and the other due to the vorticity-velocity cross-product. For simplicity, the terms in (3.7) are named as
$V$
is the velocity magnitude. In this form, the convective acceleration is broken into two parts – one due to the kinetic energy gradient, and the other due to the vorticity-velocity cross-product. For simplicity, the terms in (3.7) are named as
where
![]() $\boldsymbol{a}_{l}$
is the local acceleration, and
$\boldsymbol{a}_{l}$
is the local acceleration, and
![]() $\boldsymbol{f}_{\!i}$
,
$\boldsymbol{f}_{\!i}$
,
![]() $\boldsymbol{f}_{\!\unicode[STIX]{x1D714}}$
,
$\boldsymbol{f}_{\!\unicode[STIX]{x1D714}}$
,
![]() $\boldsymbol{f}_{\!p}$
,
$\boldsymbol{f}_{\!p}$
,
![]() $\boldsymbol{f}_{\!v}$
and
$\boldsymbol{f}_{\!v}$
and
![]() $\boldsymbol{f}_{\!\unicode[STIX]{x1D70E}}$
are the inertia force due to the kinetic energy gradient (hereafter called the inertia force), the inertia force due to the vorticity-velocity cross-product (vortex force, also known as the Lamb vector (Lamb Reference Lamb1932)), the pressure force, the viscous force and the surface tension force, all per unit mass, respectively.
$\boldsymbol{f}_{\!\unicode[STIX]{x1D70E}}$
are the inertia force due to the kinetic energy gradient (hereafter called the inertia force), the inertia force due to the vorticity-velocity cross-product (vortex force, also known as the Lamb vector (Lamb Reference Lamb1932)), the pressure force, the viscous force and the surface tension force, all per unit mass, respectively.
In cylindrical coordinates, the axial, azimuthal and radial components of the momentum equation derived in (3.7) are
where
![]() $f_{v,\unicode[STIX]{x1D70E}}$
is the combined viscous and surface tension force.
$f_{v,\unicode[STIX]{x1D70E}}$
is the combined viscous and surface tension force.
In our analysis, the four terms on the left-hand side of (3.9), (3.10) and (3.11) (a total of 12 terms) are calculated and averaged in the control volumes surrounding each wave, as was defined in figure 25. We assume that the viscous and surface tension forces are negligible compared to the others – this will be verified later. Therefore, the sum of
![]() $a_{l}$
,
$a_{l}$
,
![]() $f_{i}$
,
$f_{i}$
,
![]() $f_{\unicode[STIX]{x1D714}}$
and
$f_{\unicode[STIX]{x1D714}}$
and
![]() $f_{p}$
is approximately zero in each direction. These terms are calculated along the jet axis and are plotted in figure 34 for cases 1 and 3. The purpose of this analysis is to quantify each contributing effect in balancing the forces and accelerations, and to understand the effects of
$f_{p}$
is approximately zero in each direction. These terms are calculated along the jet axis and are plotted in figure 34 for cases 1 and 3. The purpose of this analysis is to quantify each contributing effect in balancing the forces and accelerations, and to understand the effects of
![]() $\hat{U}$
on these quantities. More specifically, we are mainly interested in the sources of pressure gradient (
$\hat{U}$
on these quantities. More specifically, we are mainly interested in the sources of pressure gradient (
![]() $f_{p}$
), which directly relates to the baroclinic vorticity generation discussed in figures 32 and 33.
$f_{p}$
), which directly relates to the baroclinic vorticity generation discussed in figures 32 and 33.

Figure 34. Comparison of the terms in the axial momentum equation (a,b), azimuthal momentum equation (c,d) and radial momentum equation (e,f), for case 1 (a,c,e) and case 3 (b,d,f);
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.
In the axial direction (figure 34
a,b), and in the UR but away from the nozzle exit (
![]() $x/D>2$
), the pressure forces (
$x/D>2$
), the pressure forces (
![]() $f_{p_{x}}$
) roughly balance the vortex forces (
$f_{p_{x}}$
) roughly balance the vortex forces (
![]() $f_{\unicode[STIX]{x1D714}_{x}}$
), while the inertia force – caused by the axial gradient of kinetic energy (
$f_{\unicode[STIX]{x1D714}_{x}}$
), while the inertia force – caused by the axial gradient of kinetic energy (
![]() $f_{i_{x}}$
) – approximately balances the local acceleration of the waves (
$f_{i_{x}}$
) – approximately balances the local acceleration of the waves (
![]() $a_{l_{x}}$
). For case 3, this one-to-one balance diminishes farther downstream (
$a_{l_{x}}$
). For case 3, this one-to-one balance diminishes farther downstream (
![]() $x/D>7.5$
), and the behaviour of the terms becomes more chaotic. This is because the waves in that range are very close to the BCR, and the vortices that are shed from the cap rim influence the flow around the waves and disturb the balance between pressure forces and inertia. Very close to the nozzle (
$x/D>7.5$
), and the behaviour of the terms becomes more chaotic. This is because the waves in that range are very close to the BCR, and the vortices that are shed from the cap rim influence the flow around the waves and disturb the balance between pressure forces and inertia. Very close to the nozzle (
![]() $x/D<2$
), the balance between the terms is disturbed again. Even though
$x/D<2$
), the balance between the terms is disturbed again. Even though
![]() $f_{p_{x}}$
still roughly balances
$f_{p_{x}}$
still roughly balances
![]() $f_{\unicode[STIX]{x1D714}_{x}}$
in this region, the magnitude of
$f_{\unicode[STIX]{x1D714}_{x}}$
in this region, the magnitude of
![]() $f_{i_{x}}$
and
$f_{i_{x}}$
and
![]() $a_{l_{x}}$
do not match. This means that the sum of these four terms is far from zero, and viscous and surface tension forces should be non-negligible in this range. This will be discussed in more detail later in this section. Overall, the magnitude of each of the four terms in the axial direction decreases as
$a_{l_{x}}$
do not match. This means that the sum of these four terms is far from zero, and viscous and surface tension forces should be non-negligible in this range. This will be discussed in more detail later in this section. Overall, the magnitude of each of the four terms in the axial direction decreases as
![]() $\hat{U}$
is increased. This is expected since the relative inertia between the gas and the liquid and, consequently, the local acceleration and axial pressure gradient decrease as
$\hat{U}$
is increased. This is expected since the relative inertia between the gas and the liquid and, consequently, the local acceleration and axial pressure gradient decrease as
![]() $\hat{U}$
increases.
$\hat{U}$
increases.
In the azimuthal direction (figure 34
c,d), all the forces are smaller compared to their axial counterparts. Unlike the axial direction, the inertia force due to the kinetic energy gradient (
![]() $f_{i_{\unicode[STIX]{x1D703}}}$
) and the vortex force (
$f_{i_{\unicode[STIX]{x1D703}}}$
) and the vortex force (
![]() $f_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}}$
) balance each other, and result in nearly zero average inertia in the
$f_{\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}}$
) balance each other, and result in nearly zero average inertia in the
![]() $\unicode[STIX]{x1D703}$
-direction and for the entire axial range. The azimuthal acceleration (
$\unicode[STIX]{x1D703}$
-direction and for the entire axial range. The azimuthal acceleration (
![]() $a_{l_{\unicode[STIX]{x1D703}}}$
) is mainly balanced by the pressure forces in the
$a_{l_{\unicode[STIX]{x1D703}}}$
) is mainly balanced by the pressure forces in the
![]() $\unicode[STIX]{x1D703}$
-direction in the UR, and also partially by the azimuthal inertia (
$\unicode[STIX]{x1D703}$
-direction in the UR, and also partially by the azimuthal inertia (
![]() $f_{i_{\unicode[STIX]{x1D703}}}$
), which is the largest of the forces. Closer to the BCR (
$f_{i_{\unicode[STIX]{x1D703}}}$
), which is the largest of the forces. Closer to the BCR (
![]() $x/D>6$
), this balance is disturbed since the viscous and surface tension forces also become significant in accelerating (or decelerating) the flow in the
$x/D>6$
), this balance is disturbed since the viscous and surface tension forces also become significant in accelerating (or decelerating) the flow in the
![]() $\unicode[STIX]{x1D703}$
-direction.
$\unicode[STIX]{x1D703}$
-direction.
Similar to the azimuthal direction, the inertia force (
![]() $f_{i_{r}}$
) and the vortex force (
$f_{i_{r}}$
) and the vortex force (
![]() $f_{\unicode[STIX]{x1D714}_{r}}$
) balance each other in the radial direction (figure 34
e,f). These two terms are two orders of magnitude larger than the pressure forces and the local acceleration, and decrease in magnitude along the axis. This decline is quicker at lower
$f_{\unicode[STIX]{x1D714}_{r}}$
) balance each other in the radial direction (figure 34
e,f). These two terms are two orders of magnitude larger than the pressure forces and the local acceleration, and decrease in magnitude along the axis. This decline is quicker at lower
![]() $\hat{U}$
(in case 1 compared to case 3). Since the vorticity is mainly in the azimuthal direction (
$\hat{U}$
(in case 1 compared to case 3). Since the vorticity is mainly in the azimuthal direction (
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) and the velocity is mainly in the axial direction (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
) and the velocity is mainly in the axial direction (
![]() $u$
), the vortex force (
$u$
), the vortex force (
![]() $\unicode[STIX]{x1D74E}\times \boldsymbol{u}$
) is mainly in the radial direction, pointing radially outward. Therefore,
$\unicode[STIX]{x1D74E}\times \boldsymbol{u}$
) is mainly in the radial direction, pointing radially outward. Therefore,
![]() $f_{\unicode[STIX]{x1D714}_{r}}$
is always positive, and is larger close to the nozzle, where both
$f_{\unicode[STIX]{x1D714}_{r}}$
is always positive, and is larger close to the nozzle, where both
![]() $u$
and
$u$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
are larger. The inertia force is always negative since the kinetic energy decreases radially outward (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
are larger. The inertia force is always negative since the kinetic energy decreases radially outward (
![]() $U_{l}>U_{g}$
). Since the kinetic energy gradient in the radial direction is higher at lower
$U_{l}>U_{g}$
). Since the kinetic energy gradient in the radial direction is higher at lower
![]() $\hat{U}$
(case 1), the magnitude of
$\hat{U}$
(case 1), the magnitude of
![]() $f_{\unicode[STIX]{x1D714}_{r}}$
is also larger. As the boundary layer (vorticity layer) thickness increases farther downstream, the radial gradient of kinetic energy decreases in magnitude. Since this decrease in
$f_{\unicode[STIX]{x1D714}_{r}}$
is also larger. As the boundary layer (vorticity layer) thickness increases farther downstream, the radial gradient of kinetic energy decreases in magnitude. Since this decrease in
![]() $f_{i_{r}}$
is faster at lower
$f_{i_{r}}$
is faster at lower
![]() $\hat{U}$
,
$\hat{U}$
,
![]() $f_{\unicode[STIX]{x1D714}_{r}}$
also decreases faster at lower
$f_{\unicode[STIX]{x1D714}_{r}}$
also decreases faster at lower
![]() $\hat{U}$
. Consequently, the magnitude of
$\hat{U}$
. Consequently, the magnitude of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
should decrease faster at lower
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
should decrease faster at lower
![]() $\hat{U}$
to make this trend happen. In this regard,
$\hat{U}$
to make this trend happen. In this regard,
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{r}$
become relatively comparable to
$\unicode[STIX]{x1D714}_{r}$
become relatively comparable to
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
in case 1, and result in faster transition towards asymmetry and more lobe stretching in case 1 compared to case 3. This results in the differences seen in the liquid surface in figure 9.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
in case 1, and result in faster transition towards asymmetry and more lobe stretching in case 1 compared to case 3. This results in the differences seen in the liquid surface in figure 9.
In case 3 (figure 34
e,f), the kinetic energy gradient remains almost constant along the axis in the UR (
![]() $x/D<7$
). This implies the gradual growth of
$x/D<7$
). This implies the gradual growth of
![]() $\unicode[STIX]{x1D6FF}_{g}$
in case 3 compared to case 1. Closer to the BCR (
$\unicode[STIX]{x1D6FF}_{g}$
in case 3 compared to case 1. Closer to the BCR (
![]() $x/D>7$
), a sudden decline in the magnitude of
$x/D>7$
), a sudden decline in the magnitude of
![]() $f_{i_{r}}$
is observed, which is mainly caused by the entrainment of the faster moving gas behind the cap. This entrainment increases the gas velocity at higher radial distances, and therefore, decreases the radial kinetic energy gradient. The sudden decline in
$f_{i_{r}}$
is observed, which is mainly caused by the entrainment of the faster moving gas behind the cap. This entrainment increases the gas velocity at higher radial distances, and therefore, decreases the radial kinetic energy gradient. The sudden decline in
![]() $f_{i_{r}}$
in case 1 at
$f_{i_{r}}$
in case 1 at
![]() $x/D\approx 4$
is also due to a similar effect. In that range, the KH wave has grown radially outward, and the gas flow that is entrained by this wave reduces the radial gradient of kinetic energy. These two scenarios can be clearly seen in figure 28(a,b).
$x/D\approx 4$
is also due to a similar effect. In that range, the KH wave has grown radially outward, and the gas flow that is entrained by this wave reduces the radial gradient of kinetic energy. These two scenarios can be clearly seen in figure 28(a,b).
The radial pressure forces and the radial local acceleration are much smaller than the inertia and vortex forces. The pressure force (
![]() $f_{p_{r}}$
) is mainly negative all along the axis and balances the local radial acceleration (
$f_{p_{r}}$
) is mainly negative all along the axis and balances the local radial acceleration (
![]() $a_{l_{r}}$
). The local radial acceleration has constant oscillations between negative and positive values along the axis. This is again due to the gas entrainment by the KH waves. The gas flows radially outward ahead of the wave and flows inward behind it. Therefore,
$a_{l_{r}}$
). The local radial acceleration has constant oscillations between negative and positive values along the axis. This is again due to the gas entrainment by the KH waves. The gas flows radially outward ahead of the wave and flows inward behind it. Therefore,
![]() $a_{l_{r}}$
is expected to have opposite signs upstream and downstream of each wave. Even though any conclusion regarding the radial viscous and surface tension forces would not be quantitatively accurate based on the results presented in figure 34(e,f), overall, it seems that
$a_{l_{r}}$
is expected to have opposite signs upstream and downstream of each wave. Even though any conclusion regarding the radial viscous and surface tension forces would not be quantitatively accurate based on the results presented in figure 34(e,f), overall, it seems that
![]() $f_{v,\unicode[STIX]{x1D70E}_{r}}$
is relatively insignificant compared to values for the axial and azimuthal directions since the four terms shown in figure 34(e,f) adequately balance one another.
$f_{v,\unicode[STIX]{x1D70E}_{r}}$
is relatively insignificant compared to values for the axial and azimuthal directions since the four terms shown in figure 34(e,f) adequately balance one another.
In order to include the effects of viscous and surface tension forces in the momentum balance discussed above, the four terms in each coordinate direction calculated above are summed to obtain
Equation (3.12) gives the magnitude of the viscous and surface tension forces per unit mass. However, to gain a better understanding of the relative significance of these forces compared to the other forces and acceleration in each direction,
![]() $\boldsymbol{f}_{\!v,\unicode[STIX]{x1D70E}}$
is normalized by the average magnitude of the other four terms. This normalized force is named
$\boldsymbol{f}_{\!v,\unicode[STIX]{x1D70E}}$
is normalized by the average magnitude of the other four terms. This normalized force is named
![]() $\unicode[STIX]{x1D731}_{v,\unicode[STIX]{x1D70E}}$
and is given by
$\unicode[STIX]{x1D731}_{v,\unicode[STIX]{x1D70E}}$
and is given by
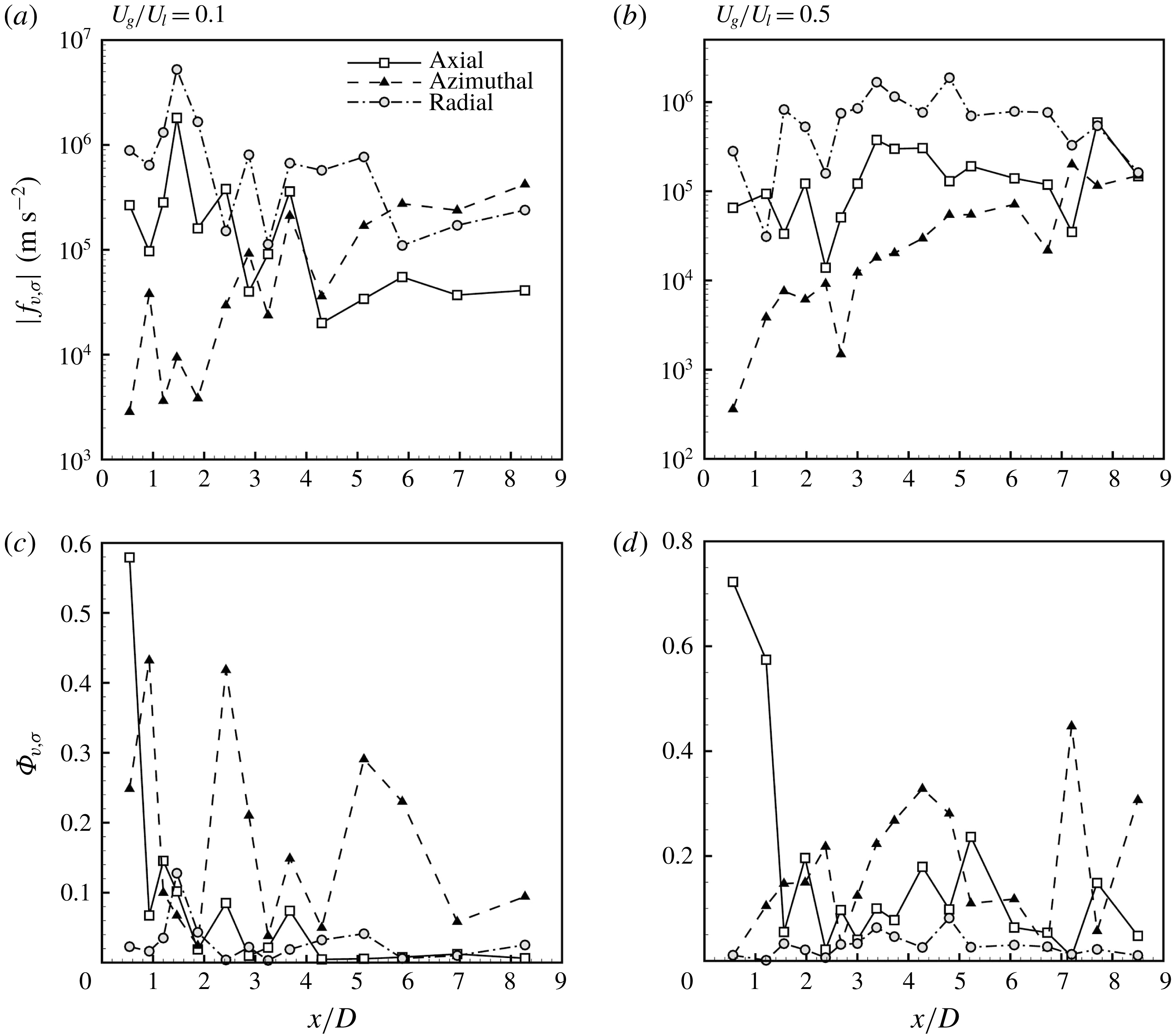
Figure 35. Comparison of viscous and surface tension forces,
![]() $|f_{v,\unicode[STIX]{x1D70E}}|$
(a,b), and normalized viscous and surface tension forces,
$|f_{v,\unicode[STIX]{x1D70E}}|$
(a,b), and normalized viscous and surface tension forces,
![]() $\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}}$
(c,d), for case 1 (a,c) and case 3 (b,d),
$\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}}$
(c,d), for case 1 (a,c) and case 3 (b,d),
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.
The absolute values of
![]() $\boldsymbol{f}_{\!v,\unicode[STIX]{x1D70E}}$
and
$\boldsymbol{f}_{\!v,\unicode[STIX]{x1D70E}}$
and
![]() $\unicode[STIX]{x1D731}_{v,\unicode[STIX]{x1D70E}}$
in the axial, azimuthal and radial directions are plotted in figure 35 for cases 1 (a,c) and 3 (b,d).
$\unicode[STIX]{x1D731}_{v,\unicode[STIX]{x1D70E}}$
in the axial, azimuthal and radial directions are plotted in figure 35 for cases 1 (a,c) and 3 (b,d).
The
![]() $f_{v,\unicode[STIX]{x1D70E}}$
components in the axial and radial directions decrease along the axis for case 1, while for case 3, they remain almost constant on average along the axis (figure 35
a,b). This is due to the fact that the growth of
$f_{v,\unicode[STIX]{x1D70E}}$
components in the axial and radial directions decrease along the axis for case 1, while for case 3, they remain almost constant on average along the axis (figure 35
a,b). This is due to the fact that the growth of
![]() $\unicode[STIX]{x1D6FF}_{g}$
is more gradual at higher
$\unicode[STIX]{x1D6FF}_{g}$
is more gradual at higher
![]() $\hat{U}$
. At lower
$\hat{U}$
. At lower
![]() $\hat{U}$
, on the other hand, the faster growth of the boundary layer implies a faster decline in the effects of viscous shear forces. Closer to the downstream range (
$\hat{U}$
, on the other hand, the faster growth of the boundary layer implies a faster decline in the effects of viscous shear forces. Closer to the downstream range (
![]() $x/D>6$
), both axial and radial
$x/D>6$
), both axial and radial
![]() $f_{v,\unicode[STIX]{x1D70E}}$
become nearly constant. Also note that
$f_{v,\unicode[STIX]{x1D70E}}$
become nearly constant. Also note that
![]() $f_{v,\unicode[STIX]{x1D70E}_{r}}$
is larger than
$f_{v,\unicode[STIX]{x1D70E}_{r}}$
is larger than
![]() $f_{v,\unicode[STIX]{x1D70E}_{x}}$
in both cases, likely because a larger
$f_{v,\unicode[STIX]{x1D70E}_{x}}$
in both cases, likely because a larger
![]() $f_{v_{r}}$
is required to balance the much larger kinetic energy gradient in
$f_{v_{r}}$
is required to balance the much larger kinetic energy gradient in
![]() $r\;(O(10^{7})~\text{m}~\text{s}^{-2})$
, whereas the axial gradient of kinetic energy is much smaller (
$r\;(O(10^{7})~\text{m}~\text{s}^{-2})$
, whereas the axial gradient of kinetic energy is much smaller (
![]() $O(10^{6})~\text{m}~\text{s}^{-2}$
) and requires less viscous force to balance.
$O(10^{6})~\text{m}~\text{s}^{-2}$
) and requires less viscous force to balance.
Unlike the other two components,
![]() $f_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
increases with
$f_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
increases with
![]() $x$
. It is known that the viscous diffusion and surface tension forces tend to resist and damp the surface instability. Since the azimuthal instabilities grow in
$x$
. It is known that the viscous diffusion and surface tension forces tend to resist and damp the surface instability. Since the azimuthal instabilities grow in
![]() $x$
, larger viscous and surface tension forces are required to resist the azimuthal surface deformation away from the axisymmetry. Since the inertia forces are larger at lower
$x$
, larger viscous and surface tension forces are required to resist the azimuthal surface deformation away from the axisymmetry. Since the inertia forces are larger at lower
![]() $\hat{U}$
, a larger viscous force is formed to balance the azimuthal inertia. Therefore,
$\hat{U}$
, a larger viscous force is formed to balance the azimuthal inertia. Therefore,
![]() $f_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is larger in case 1 than in case 3.
$f_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is larger in case 1 than in case 3.
To better delineate the importance of viscosity and surface tension in each case,
![]() $\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}}$
is plotted in figure 35(c,d). Even though
$\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}}$
is plotted in figure 35(c,d). Even though
![]() $f_{v,\unicode[STIX]{x1D70E}_{r}}$
is the largest of the three components,
$f_{v,\unicode[STIX]{x1D70E}_{r}}$
is the largest of the three components,
![]() $\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{r}}$
is the smallest, mainly because the other forces, i.e. inertia, vortex and pressure forces, are much larger in the radial direction. This is in line with our earlier conclusion made in the discussion of figure 34(e,f). The value of
$\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{r}}$
is the smallest, mainly because the other forces, i.e. inertia, vortex and pressure forces, are much larger in the radial direction. This is in line with our earlier conclusion made in the discussion of figure 34(e,f). The value of
![]() $f_{v,\unicode[STIX]{x1D70E}_{r}}$
is less than 10 % of the average of the other four terms and is negligible in the radial direction at all
$f_{v,\unicode[STIX]{x1D70E}_{r}}$
is less than 10 % of the average of the other four terms and is negligible in the radial direction at all
![]() $x$
.
$x$
.
As mentioned earlier, and now verified, the axial viscous and surface tension forces are considerable only very close to the nozzle, i.e.
![]() $x/D<2$
. In that range,
$x/D<2$
. In that range,
![]() $f_{v,\unicode[STIX]{x1D70E}_{x}}$
is about 60 % and 75 % of the average value of the other terms in cases 1 and 3, respectively. With the growth of
$f_{v,\unicode[STIX]{x1D70E}_{x}}$
is about 60 % and 75 % of the average value of the other terms in cases 1 and 3, respectively. With the growth of
![]() $\unicode[STIX]{x1D6FF}_{g}$
, the relative importance of the axial viscous force drops suddenly and remains low for the rest of the domain. In case 3 compared to case 1,
$\unicode[STIX]{x1D6FF}_{g}$
, the relative importance of the axial viscous force drops suddenly and remains low for the rest of the domain. In case 3 compared to case 1,
![]() $f_{v_{x}}$
is dominant. This is expected because the inertia force is significantly larger in case 1 than in case 3, and
$f_{v_{x}}$
is dominant. This is expected because the inertia force is significantly larger in case 1 than in case 3, and
![]() $Re_{r}$
in case 3 is nearly one half of that in case 1.
$Re_{r}$
in case 3 is nearly one half of that in case 1.
For both cases along the entire axis,
![]() $\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is quite large and not negligible. Even though
$\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is quite large and not negligible. Even though
![]() $f_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is the smallest of the viscous forces, the relative importance of this force is much more significant compared to
$f_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is the smallest of the viscous forces, the relative importance of this force is much more significant compared to
![]() $f_{v,\unicode[STIX]{x1D70E}_{x}}$
and
$f_{v,\unicode[STIX]{x1D70E}_{x}}$
and
![]() $f_{v,\unicode[STIX]{x1D70E}_{r}}$
. This is because the inertia, vortex and pressure forces are much smaller in the azimuthal direction than in the axial and radial directions. Overall,
$f_{v,\unicode[STIX]{x1D70E}_{r}}$
. This is because the inertia, vortex and pressure forces are much smaller in the azimuthal direction than in the axial and radial directions. Overall,
![]() $\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
ranges from 5 %–40 % in case 1, and from 5 %–30% in case 3 (figure 35
c,d). The pronounced oscillations in
$\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
ranges from 5 %–40 % in case 1, and from 5 %–30% in case 3 (figure 35
c,d). The pronounced oscillations in
![]() $\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is related to the small denominator in the
$\unicode[STIX]{x1D6F7}_{v,\unicode[STIX]{x1D70E}_{\unicode[STIX]{x1D703}}}$
is related to the small denominator in the
![]() $\unicode[STIX]{x1D703}$
-direction.
$\unicode[STIX]{x1D703}$
-direction.
The main conclusion here is that the radial pressure gradient is the dominant factor in the growth of the baroclicnic term (compared to the radial density gradient). As shown in § 3.5,
![]() $\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r$
is larger at lower
$\unicode[STIX]{x2202}p/\unicode[STIX]{x2202}r$
is larger at lower
![]() $\hat{U}$
because of the larger relative velocity between the gas and the liquid. As shown in this section, the radial pressure force roughly balances the radial acceleration. Since
$\hat{U}$
because of the larger relative velocity between the gas and the liquid. As shown in this section, the radial pressure force roughly balances the radial acceleration. Since
![]() $\unicode[STIX]{x1D714}_{r}$
is larger at lower
$\unicode[STIX]{x1D714}_{r}$
is larger at lower
![]() $\hat{U}$
, the radial growth of the waves is higher; therefore, the radial acceleration is also higher at low
$\hat{U}$
, the radial growth of the waves is higher; therefore, the radial acceleration is also higher at low
![]() $\hat{U}$
. Consequently,
$\hat{U}$
. Consequently,
![]() $f_{p_{r}}$
is larger and the baroclinic effects are greater. Farther downstream and with the growth of liquid lobes, the azimuthal pressure gradient also grows, becoming comparable to the radial pressure force. At lower
$f_{p_{r}}$
is larger and the baroclinic effects are greater. Farther downstream and with the growth of liquid lobes, the azimuthal pressure gradient also grows, becoming comparable to the radial pressure force. At lower
![]() $\hat{U}$
,
$\hat{U}$
,
![]() $f_{p_{\unicode[STIX]{x1D703}}}$
grows faster. At high
$f_{p_{\unicode[STIX]{x1D703}}}$
grows faster. At high
![]() $\hat{U}$
(case 3), the lower relative inertia between the gas and the liquid is not able to easily deform the interface in the azimuthal direction, and
$\hat{U}$
(case 3), the lower relative inertia between the gas and the liquid is not able to easily deform the interface in the azimuthal direction, and
![]() $\unicode[STIX]{x2202}p/(r\unicode[STIX]{x2202}\unicode[STIX]{x1D703})$
does not get much larger than the radial density gradient (figure 33
b). Therefore, at high
$\unicode[STIX]{x2202}p/(r\unicode[STIX]{x2202}\unicode[STIX]{x1D703})$
does not get much larger than the radial density gradient (figure 33
b). Therefore, at high
![]() $\hat{U}$
,
$\hat{U}$
,
![]() $\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r$
is as effective as the azimuthal pressure forces in the baroclinic vortex generation in the downstream range.
$\unicode[STIX]{x2202}\unicode[STIX]{x1D70C}/\unicode[STIX]{x2202}r$
is as effective as the azimuthal pressure forces in the baroclinic vortex generation in the downstream range.
3.7 Impact of the gas–liquid relative velocity
To better delineate the impact of gas–liquid relative velocity (and velocity ratio) on the vortex generation and consequently the surface deformation, case 4 is analysed and compared with cases 2 and 3 in this section. As indicated in table 1, case 4 has a higher liquid velocity (
![]() $U_{l}=80~\text{m}~\text{s}^{-1}$
) compared to the other three cases. The gas velocity (
$U_{l}=80~\text{m}~\text{s}^{-1}$
) compared to the other three cases. The gas velocity (
![]() $U_{g}=40~\text{m}~\text{s}^{-1}$
) is chosen such that case 4 has the same velocity ratio (
$U_{g}=40~\text{m}~\text{s}^{-1}$
) is chosen such that case 4 has the same velocity ratio (
![]() $\hat{U}=0.5$
) as in case 3, but the same relative velocity (and the same
$\hat{U}=0.5$
) as in case 3, but the same relative velocity (and the same
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
) as in case 2. Therefore, comparison between these three cases would help us understand which of these quantities, i.e.
$We_{r}$
) as in case 2. Therefore, comparison between these three cases would help us understand which of these quantities, i.e.
![]() $\hat{U}$
or
$\hat{U}$
or
![]() $U_{r}$
, is better for describing similarity of the atomization process and vortex generation in the cascade process.
$U_{r}$
, is better for describing similarity of the atomization process and vortex generation in the cascade process.
This analysis also helps with identifying the atomization domains in coaxial jets. So far, we only presumed that the domains can be identified based on
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
values, without the inclusion of
$We_{r}$
values, without the inclusion of
![]() $\hat{U}$
as the third defining dimensionless quantity (see figure 22). Composition of diagrams that would identify different atomization domains (regimes) can be much more complicated in coaxial jets compared to jets with no coaxial flow since one has to deal with a much larger number of dimensionless quantities (e.g. velocity ratio and momentum flux ratio). Farago & Chigier (Reference Farago and Chigier1992) were among the first to establish such a diagram for coaxial jets; however, they used only
$\hat{U}$
as the third defining dimensionless quantity (see figure 22). Composition of diagrams that would identify different atomization domains (regimes) can be much more complicated in coaxial jets compared to jets with no coaxial flow since one has to deal with a much larger number of dimensionless quantities (e.g. velocity ratio and momentum flux ratio). Farago & Chigier (Reference Farago and Chigier1992) were among the first to establish such a diagram for coaxial jets; however, they used only
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
for this purpose and excluded the effects of velocity ratio and/or momentum flux ratio. Their analysis and experiments were limited to very low
$We_{g}$
for this purpose and excluded the effects of velocity ratio and/or momentum flux ratio. Their analysis and experiments were limited to very low
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
, which were mainly in the Rayleigh and wind-induced regimes. A more complete diagram was later produced by Hopfinger (Reference Hopfinger1998) with the inclusion of momentum flux ratio,
$We_{g}$
, which were mainly in the Rayleigh and wind-induced regimes. A more complete diagram was later produced by Hopfinger (Reference Hopfinger1998) with the inclusion of momentum flux ratio,
![]() $M=\unicode[STIX]{x1D70C}_{g}U_{g}^{2}/\unicode[STIX]{x1D70C}_{l}U_{l}^{2}$
, on a
$M=\unicode[STIX]{x1D70C}_{g}U_{g}^{2}/\unicode[STIX]{x1D70C}_{l}U_{l}^{2}$
, on a
![]() $Re_{l}$
-
$Re_{l}$
-
![]() $We_{g}$
diagram. Later, Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000) verified the same diagram with more case studies and at higher
$We_{g}$
diagram. Later, Lasheras & Hopfinger (Reference Lasheras and Hopfinger2000) verified the same diagram with more case studies and at higher
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
values for air-blast atomization. They were able to identify three types of breakup, namely, shear breakup (similar to our domain I), membrane breakup (similar to hole formation) and fibre-type atomization which occurs at higher
$We_{g}$
values for air-blast atomization. They were able to identify three types of breakup, namely, shear breakup (similar to our domain I), membrane breakup (similar to hole formation) and fibre-type atomization which occurs at higher
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
and results in finer spray. No discussion was provided regarding the cause of different breakup mechanisms from the vortex dynamics perspective.
$We_{g}$
and results in finer spray. No discussion was provided regarding the cause of different breakup mechanisms from the vortex dynamics perspective.

Figure 36. Axial distribution of
![]() $\unicode[STIX]{x1D714}_{x}$
(a) and
$\unicode[STIX]{x1D714}_{x}$
(a) and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(b) for cases 2, 3 and 4, at
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
(b) for cases 2, 3 and 4, at
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.
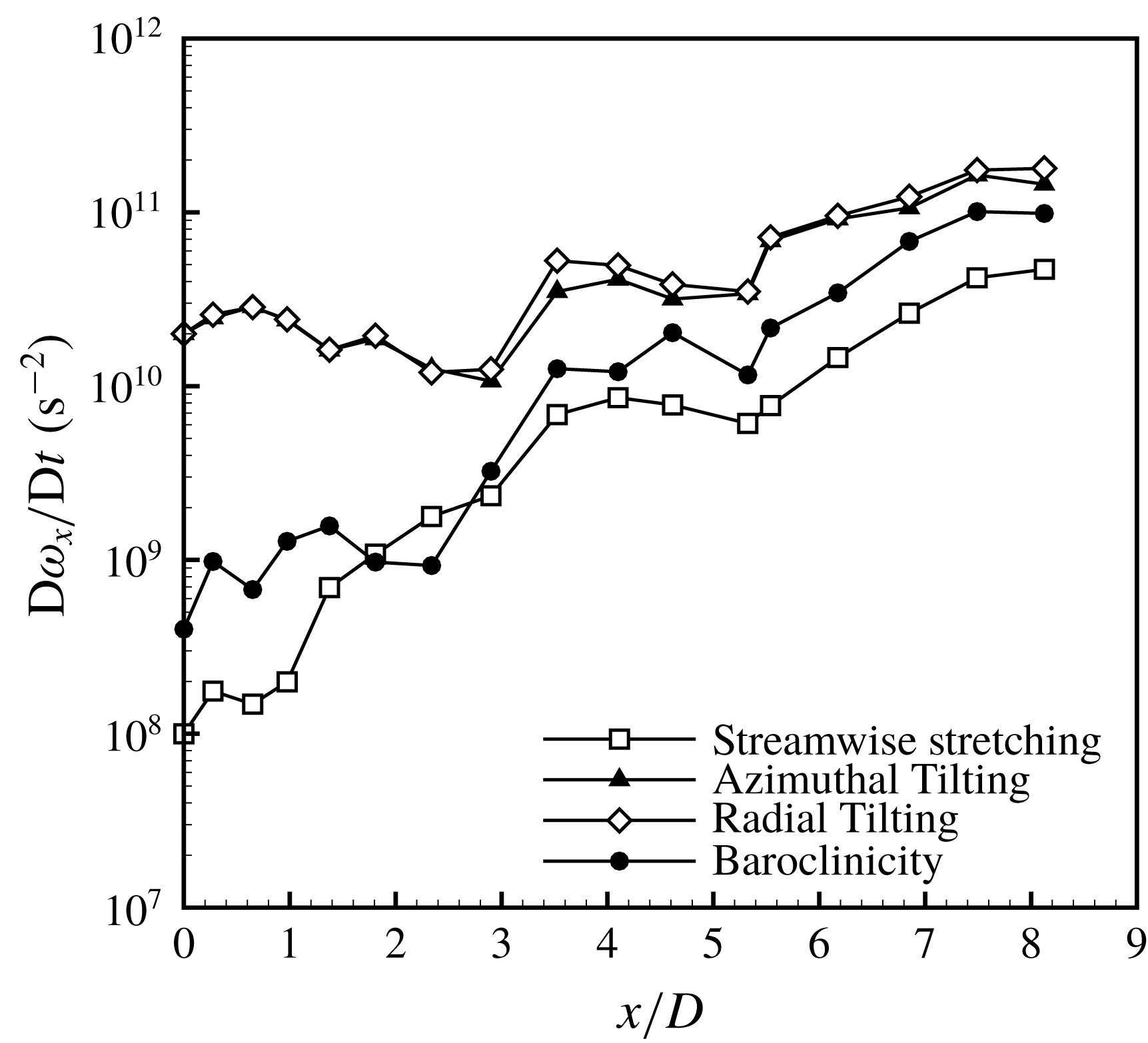
Figure 37. Contributions of streamwise vortex stretching, azimuthal vortex tilting, radial vortex tilting and baroclinicity to the generation of
![]() $\unicode[STIX]{x1D714}_{x}$
at the jet surface for case 4;
$\unicode[STIX]{x1D714}_{x}$
at the jet surface for case 4;
![]() $t^{\ast }=11.5$
.
$t^{\ast }=11.5$
.
Figure 36 compares the axial distribution of
![]() $\unicode[STIX]{x1D714}_{x}$
and
$\unicode[STIX]{x1D714}_{x}$
and
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
for cases 2, 3 and 4. Both plots clearly indicate that both vorticity components in case 4 follow the same path and growth as in case 2, whereas case 3 has a much lower and more distinct vorticity distribution. This clearly indicates that the velocity difference (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
for cases 2, 3 and 4. Both plots clearly indicate that both vorticity components in case 4 follow the same path and growth as in case 2, whereas case 3 has a much lower and more distinct vorticity distribution. This clearly indicates that the velocity difference (
![]() $U_{r}$
) is a much more relevant factor in determining the growth or decay of vortices compared to the velocity ratio. Case 4 only has a slightly larger
$U_{r}$
) is a much more relevant factor in determining the growth or decay of vortices compared to the velocity ratio. Case 4 only has a slightly larger
![]() $\unicode[STIX]{x1D714}_{x}$
growth rate and a slightly larger
$\unicode[STIX]{x1D714}_{x}$
growth rate and a slightly larger
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
decay rate compared to case 2. This difference is negligible compared to the very different distribution seen in case 3. The maximum azimuthal vorticity (
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}}$
decay rate compared to case 2. This difference is negligible compared to the very different distribution seen in case 3. The maximum azimuthal vorticity (
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
) close to the nozzle exit also compares well in cases 2 and 4. This indicates that our earlier definition of
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
) close to the nozzle exit also compares well in cases 2 and 4. This indicates that our earlier definition of
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}=U_{r}/\unicode[STIX]{x1D6FF}_{g}$
is also quite accurate, since both cases 2 and 4 have the same
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}=U_{r}/\unicode[STIX]{x1D6FF}_{g}$
is also quite accurate, since both cases 2 and 4 have the same
![]() $U_{r}$
and they result in the same
$U_{r}$
and they result in the same
![]() $\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
.
$\unicode[STIX]{x1D714}_{\unicode[STIX]{x1D703}_{max}}$
.
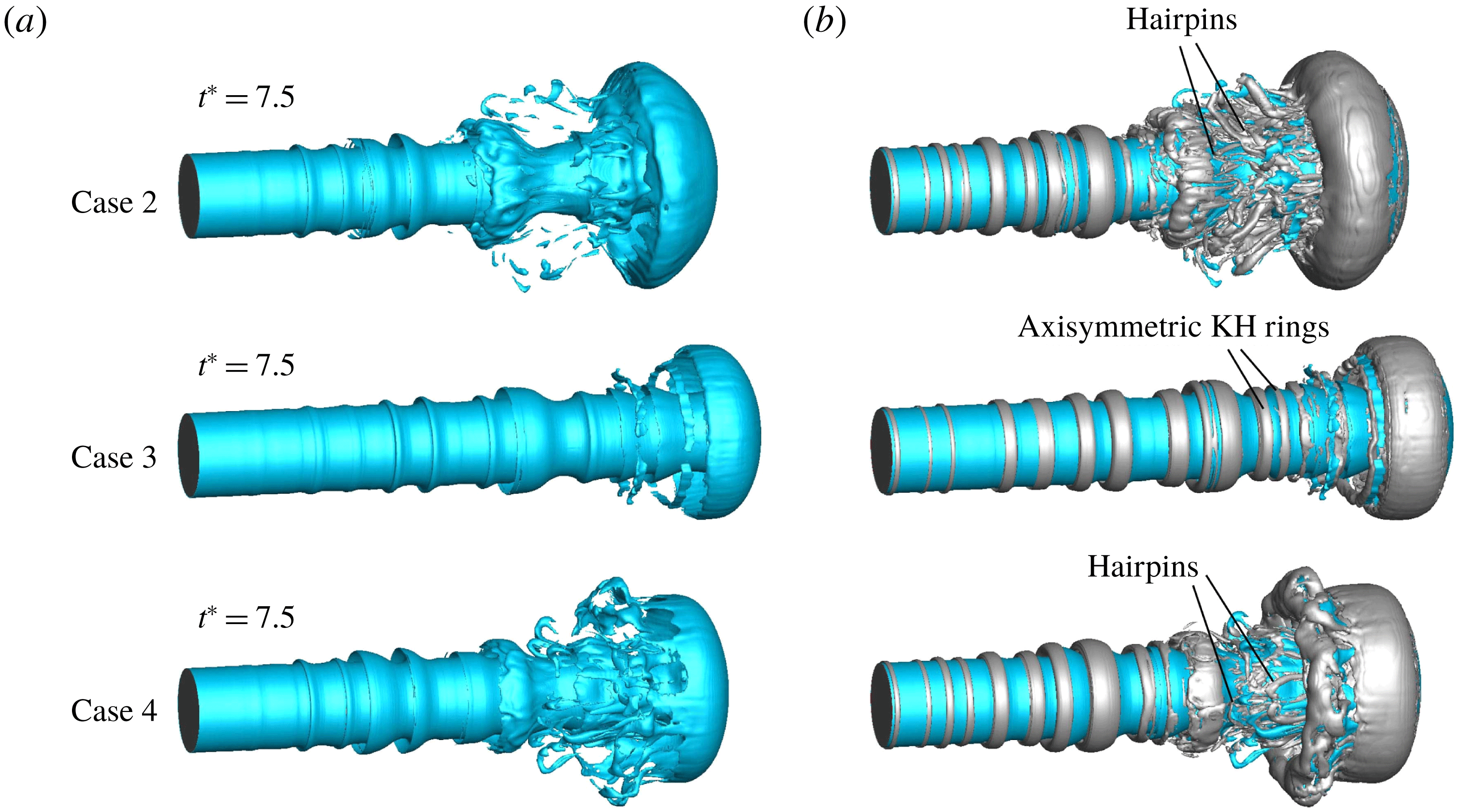
Figure 38. Liquid-jet surfaces (a), and the vortex structures (b) in case 2 (top), case 3 (centre) and case 4 (bottom);
![]() $t^{\ast }=7.5$
.
$t^{\ast }=7.5$
.
To further explore the details of
![]() $\unicode[STIX]{x1D714}_{x}$
generation in case 4, the contribution of the four vortex generating mechanisms, i.e. streamwise vortex stretching, azimuthal vortex tilting, radial vortex tilting, and baroclinic vortex generation, are plotted along the
$\unicode[STIX]{x1D714}_{x}$
generation in case 4, the contribution of the four vortex generating mechanisms, i.e. streamwise vortex stretching, azimuthal vortex tilting, radial vortex tilting, and baroclinic vortex generation, are plotted along the
![]() $x$
-axis in figure 37. Other than the vortex tilting terms that have the largest but similar magnitudes (with opposite signs), baroclinicity is more effective than streamwise stretching in case 4. Comparing figure 37 with figure 29(b,c), it becomes clear that the
$x$
-axis in figure 37. Other than the vortex tilting terms that have the largest but similar magnitudes (with opposite signs), baroclinicity is more effective than streamwise stretching in case 4. Comparing figure 37 with figure 29(b,c), it becomes clear that the
![]() $\unicode[STIX]{x1D714}_{x}$
generating effect is also very similar for cases 4 and 2. This supports the conclusion that
$\unicode[STIX]{x1D714}_{x}$
generating effect is also very similar for cases 4 and 2. This supports the conclusion that
![]() $U_{r}$
(embedded in
$U_{r}$
(embedded in
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
) is more significant than
$We_{r}$
) is more significant than
![]() $\hat{U}$
in determining the quantitative growth of the vorticity components.
$\hat{U}$
in determining the quantitative growth of the vorticity components.
Figure 38 shows that the similarity of the quantitative measures of vorticity components in cases 2 and 4 is also reflected in the vortex structures and consequently the liquid-jet surface in these two cases. Both cases 2 and 4 show the formation of hairpin vortex structures near the jet cap, and a much earlier transition towards asymmetry in the KH vortex rings farther upstream (figure 38 b), while vortex rings in case 3 are still fairly axisymmetric with no signs of axial stretching at the same dimensionless time. This similarity in the vortex formation and interaction is also reflected in the surface deformation. Both cases 2 and 4 indicate signs of lobe formation and thinning along the location of hairpin vortices, while the caps are also more enlarged by growth and torn in both cases compared to case 2, which still experiences axisymmetric growth with fewer 3-D instabilities and asymmetric deformations (figure 38 a).

Figure 39. Comparison of the liquid-jet surface in case 2 (a) and case 4 (b) at
![]() $t^{\ast }=15$
. The liquid surfaces are coloured with streamwise velocity contours.
$t^{\ast }=15$
. The liquid surfaces are coloured with streamwise velocity contours.
The surface structures of cases 2 and 4 stay similar at a much later time,
![]() $t^{\ast }=15$
, when the cap has moved out of the domain. Figure 39 shows very similar surface structures in both cases 2 and 4 on the jet stem. Even though the liquid surface velocity in case 4 is almost twice that of case 2, both show similar lobe formation, lobe thinning, hole formation, bridge breakup and ligament formation in their cascade process. The clear conclusion here is that the atomization domains that were introduced earlier for temporal flow by ZSH1 based on
$t^{\ast }=15$
, when the cap has moved out of the domain. Figure 39 shows very similar surface structures in both cases 2 and 4 on the jet stem. Even though the liquid surface velocity in case 4 is almost twice that of case 2, both show similar lobe formation, lobe thinning, hole formation, bridge breakup and ligament formation in their cascade process. The clear conclusion here is that the atomization domains that were introduced earlier for temporal flow by ZSH1 based on
![]() $Re_{l}$
and
$Re_{l}$
and
![]() $We_{g}$
can be generalized to include spatially developing coaxial flows by use of relative velocity for the Reynolds and Weber numbers, i.e.
$We_{g}$
can be generalized to include spatially developing coaxial flows by use of relative velocity for the Reynolds and Weber numbers, i.e.
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
. Defined this way, cases 2 and 4 appear at exactly the same location on the
$We_{r}$
. Defined this way, cases 2 and 4 appear at exactly the same location on the
![]() $We_{r}$
versus
$We_{r}$
versus
![]() $Re_{r}$
plot (figure 22) and fall in domain II, whereas case 3 falls under domain I with a different cascade process involving no hole formation.
$Re_{r}$
plot (figure 22) and fall in domain II, whereas case 3 falls under domain I with a different cascade process involving no hole formation.
This new criterion for domain decomposition based on
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
simplifies the categorization of atomization regimes that were introduced before (Farago & Chigier Reference Farago and Chigier1992; Hopfinger Reference Hopfinger1998; Lasheras & Hopfinger Reference Lasheras and Hopfinger2000). Our results indicate that if the relative velocity is used for defining Reynolds and Weber numbers, there is no need for inclusion of a third dimensionless parameter, such as velocity ratio or momentum flux ratio, to distinguish between different cases. Our conclusion here addresses only events up to a certain time in the atomization process. The identification of the precise location of the boundaries between the different atomization domains to any degree of accuracy requires much more experimental and numerical data than is currently available. This requires a more detailed analysis of wider ranges of
$We_{r}$
simplifies the categorization of atomization regimes that were introduced before (Farago & Chigier Reference Farago and Chigier1992; Hopfinger Reference Hopfinger1998; Lasheras & Hopfinger Reference Lasheras and Hopfinger2000). Our results indicate that if the relative velocity is used for defining Reynolds and Weber numbers, there is no need for inclusion of a third dimensionless parameter, such as velocity ratio or momentum flux ratio, to distinguish between different cases. Our conclusion here addresses only events up to a certain time in the atomization process. The identification of the precise location of the boundaries between the different atomization domains to any degree of accuracy requires much more experimental and numerical data than is currently available. This requires a more detailed analysis of wider ranges of
![]() $Re_{r}$
and
$Re_{r}$
and
![]() $We_{r}$
than possible now.
$We_{r}$
than possible now.
4 Concluding remarks
A three-dimensional round liquid jet with coaxial, outer gas flow is numerically simulated and analysed. The evolution of instabilities on the gas–liquid interface is observed to be correlated with the vortex interactions around the gas–liquid interface using a
![]() $\unicode[STIX]{x1D706}_{2}$
analysis. Two main regions were identified on the liquid jet, separated by a large indentation on the jet stem, with distinguished surface deformations and vortex interactions. The BCR is inside the recirculation zone behind the mushroom-shaped cap. The KH waves formed in the BCR roll downstream until they coalesce with the cap. The BCR vortices and surface deformations are not periodic and are controlled by the dynamics of vortices in the recirculation zone. The second region (upstream region) is farther upstream of the cap. The gas flow, while undergoing Tollmien–Schlichting instability over the smooth liquid surface, is slower than the liquid jet in the UR, and the shear caused by this relative gas stream triggers KH vortex rings. The UR deformations are periodic and can be portrayed well in a frame moving with the convective velocity of the jet, which validates the earlier temporal studies with periodic boundary conditions. The relative gas–liquid velocity is the relevant characteristic velocity for the liquid Reynolds number and gas Weber number in coannular jets. Using this definition, the atomization domains are identified well on a
$\unicode[STIX]{x1D706}_{2}$
analysis. Two main regions were identified on the liquid jet, separated by a large indentation on the jet stem, with distinguished surface deformations and vortex interactions. The BCR is inside the recirculation zone behind the mushroom-shaped cap. The KH waves formed in the BCR roll downstream until they coalesce with the cap. The BCR vortices and surface deformations are not periodic and are controlled by the dynamics of vortices in the recirculation zone. The second region (upstream region) is farther upstream of the cap. The gas flow, while undergoing Tollmien–Schlichting instability over the smooth liquid surface, is slower than the liquid jet in the UR, and the shear caused by this relative gas stream triggers KH vortex rings. The UR deformations are periodic and can be portrayed well in a frame moving with the convective velocity of the jet, which validates the earlier temporal studies with periodic boundary conditions. The relative gas–liquid velocity is the relevant characteristic velocity for the liquid Reynolds number and gas Weber number in coannular jets. Using this definition, the atomization domains are identified well on a
![]() $We_{r}$
–
$We_{r}$
–
![]() $Re_{r}$
diagram without the need of any extra dimensionless parameter such as velocity ratio, which is widely used in the literature. The hole formation mechanism at high
$Re_{r}$
diagram without the need of any extra dimensionless parameter such as velocity ratio, which is widely used in the literature. The hole formation mechanism at high
![]() $We_{r}$
and
$We_{r}$
and
![]() $Re_{r}$
ranges, and lobe stretching domain at lower
$Re_{r}$
ranges, and lobe stretching domain at lower
![]() $We_{r}$
and
$We_{r}$
and
![]() $Re_{r}$
are well captured in this diagram.
$Re_{r}$
are well captured in this diagram.
After the KH instability develops, baroclinicity is the most important cause of streamwise vorticity generation in the practical range of density ratios, while the streamwise vortex stretching becomes more important only at lower relative velocities where pressure gradients are smaller. The pressure force roughly balances the vortex force in the axial direction, while the inertia force due to the axial gradient of kinetic energy is mainly responsible for the axial acceleration of the waves. In the azimuthal direction, the inertia force due to kinetic energy gradient balances the vortex force causing nearly zero azimuthal inertia. The local azimuthal acceleration is mainly caused by the pressure force in the UR. The radial inertia force decreases with the growth of vorticity-layer thickness downstream. This drop occurs faster at higher relative velocity, which results in a much faster decrease in the azimuthal vorticity, and a faster transition towards asymmetry and growth of azimuthal instabilities. The radial viscous forces are negligible throughout, while the axial viscous forces are very important close to the nozzle but are negligible further downstream. The azimuthal viscous forces, however, cannot be neglected even at higher
![]() $Re_{r}$
(in the ranges studied here) because they are always comparable to the pressure, inertia and vortex forces in the azimuthal direction. This indicates that inertia is not totally dominant in 3-D instabilities in primary atomization.
$Re_{r}$
(in the ranges studied here) because they are always comparable to the pressure, inertia and vortex forces in the azimuthal direction. This indicates that inertia is not totally dominant in 3-D instabilities in primary atomization.
Acknowledgements
Access to the XSEDE supercomputer under Allocation CTS170036 and to the UCI HPC cluster were very valuable in performing our high resolution computations.