Hostname: page-component-78c5997874-4rdpn Total loading time: 0 Render date: 2024-11-14T16:16:09.077Z Has data issue: false hasContentIssue false
  • English
  • Français

Wake vortex evolution of square cylinder with a slot synthetic jet positioned at the rear surface

Published online by Cambridge University Press:  09 January 2017

Yuan Qu ,
Jinjun Wang ,
Mao Sun ,
Lihao Feng ,
Chong Pan ,
Qi Gao  and
Guosheng He
Yuan Qu
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Jinjun Wang*
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Mao Sun
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Lihao Feng
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Chong Pan
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Qi Gao
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
Guosheng He
Affiliation:
Key Laboratory of Fluid Mechanics (Beijing University of Aeronautics and Astronautics), Ministry of Education, Beijing 100191, China
*
†Email address for correspondence: jjwang@buaa.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

Wake vortex evolution of a square cylinder with a slot synthetic jet issuing from the cylinder’s rear surface has been experimentally investigated using the time-resolved particle image velocimetry technique. The Reynolds number based on the side length of the square cylinder is 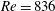$Re=836$. The excitation frequency normalized by the natural shedding frequency 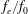$f_{e}/f_{0}$ varies from 0 to 6 at the dimensionless stroke length 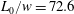$L_{0}/w=72.6$. The distributions of the time-averaged Reynolds stresses present significant differences as the excitation frequency increases. With control, the mean streamwise velocity deficit of the wake recovers more quickly in comparison with the natural case, and the vertical velocity fluctuation intensity becomes weaker. Moreover, a drag reduction can be achieved for the control cases, especially, for 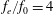$f_{e}/f_{0}=4$ and 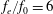$f_{e}/f_{0}=6$, a thrust instead of drag reduction can be obtained. The profiles of the mean streamwise velocity tend to have jet-like distributions. The wake vortex dynamics and its evolution with the excitation frequency are revealed. (i) For the low excitation frequency cases (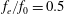$f_{e}/f_{0}=0.5$, 1, 2), no significant changes in the dominant frequency and the spanwise vortex structures are observed in comparison with the natural case. (ii) For the moderate excitation frequency case (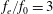$f_{e}/f_{0}=3$), the wake vortex shedding frequency is locked on half of the control frequency. In this case, the shear layer is divided into two parts by the synthetic jet vortex, and the wake vortices with smaller scales still shed asymmetrically and appear closer to the square cylinder. (iii) For the high excitation frequency case (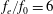$f_{e}/f_{0}=6$), the flow is governed by the synthetic jet. As a result of strong perturbations of the synthetic jet, the wake vortex shedding becomes symmetric with the shedding frequency consistent with the control frequency. And the separation is suppressed effectively. The different control effects of the slot synthetic jet on a square cylinder and a circular cylinder are also compared in detail. Generally speaking, the circular cylinder is easier to be controlled due to its non-fixed separation points.

JFM classification

Wakes/Jets: Separated flows Vortex Flows: Vortex dynamics Wakes/Jets: Wakes/Jets
Type
Papers
Information
Journal of Fluid Mechanics , Volume 812 , 10 February 2017 , pp. 940 - 965
Check for updates
Copyright
© 2017 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Akansu, Y. E. & Firat, E. 2010 Control of flow around a square prism by slot jet injection from the rear surface. Exp. Therm. Fluid Sci. 34 (7), 906–914.Google Scholar
Ali, M. S. M., Doolan, C. J. & Wheatley, V. 2011 Low Reynolds number flow over a square cylinder with a splitter plate. Phys. Fluids 23 (3), 033602.Google Scholar
Amitay, M. & Cannelle, F. 2006 Evolution of finite span synthetic jets. Phys. Fluids 18 (5), 054101.CrossRefGoogle Scholar
Antonia, R. A. & Rajagopalan, S. 1990 Determination of drag of a circular cylinder. AIAA J. 28 (10), 1833–1834.Google Scholar
Baj, P., Bruce, P. J. K. & Buxton, O. R. H. 2015 The triple decomposition of a fluctuating velocity field in a multiscale flow. Phys. Fluids 27 (7), 075104.Google Scholar
Balachandar, S., Mittal, R. & Najjar, F. M. 1997 Properties of the mean recirculation region in the wakes of two-dimensional bluff bodies. J. Fluid Mech. 351, 167–199.CrossRefGoogle Scholar
Bearman, P. W. & Trueman, D. M. 1972 An investigation of the flow around rectangular cylinders. Aeronaut. Q 23, 229–237.CrossRefGoogle Scholar
Berkooz, G., Holmes, P. & Lumley, J. L. 1993 The proper orthogonal decomposition in the analysis of turbulent flows. Annu. Rev. Fluid Mech. 25 (1), 539–575.CrossRefGoogle Scholar
Champagnat, F., Plyer, A., Le Besnerais, G., Leclaire, B., Davoust, S. & Le Sant, Y. 2011 Fast and accurate PIV computation using highly parallel iterative correlation maximization. Exp. Fluids 50 (4), 1169–1182.CrossRefGoogle Scholar
Chatterjee, A. 2000 An introduction to the proper orthogonal decomposition. Curr. Sci. 78 (7), 808–817.Google Scholar
Choi, H., Jeon, W. P. & Kim, J. 2008 Control of flow over a bluff body. Annu. Rev. Fluid Mech. 40, 113–139.CrossRefGoogle Scholar
Dipankar, A., Sengupta, T. K. & Talla, S. B. 2007 Suppression of vortex shedding behind a circular cylinder by another control cylinder at low Reynolds numbers. J. Fluid Mech. 573, 171–190.Google Scholar
Feng, L. H., Ma, L. Q. & Wang, J. J. 2014 End-effects of a finite synthetic jet on flow control. In Fluid-Structure-Sound Interactions and Control, pp. 129–134. Springer.Google Scholar
Feng, L. H. & Wang, J. J. 2010 Circular cylinder vortex-synchronization control with a synthetic jet positioned at the rear stagnation point. J. Fluid Mech. 662, 232–259.Google Scholar
Feng, L. H., Wang, J. J. & Pan, C. 2011 Proper orthogonal decomposition analysis of vortex dynamics of a circular cylinder under synthetic jet control. Phys. Fluids 23 (1), 014106.CrossRefGoogle Scholar
Gerrard, J. H. 1966 The mechanics of the formation region of vortices behind bluff bodies. J. Fluid Mech. 25 (02), 401–413.Google Scholar
Glezer, A. 1988 The formation of vortex rings. Phys. Fluids 31 (12), 3532–3542.Google Scholar
He, G. S., Li, N. & Wang, J. J. 2014 Drag reduction of square cylinders with cut-corners at the front edges. Exp. Fluids 55 (6), 1–11.CrossRefGoogle Scholar
Hosseini, Z., Bourgeois, J. A. & Martinuzzi, R. J. 2013 Large-scale structures in dipole and quadrupole wakes of a wall-mounted finite rectangular cylinder. Exp. Fluids 54 (9), 1–16.CrossRefGoogle Scholar
Hu, J. C., Zhou, Y. & Dalton, C. 2006 Effects of the corner radius on the near wake of a square prism. Exp. Fluids 40 (1), 106–118.Google Scholar
Huang, R. F., Hsu, C. M. & Chiu, P. C. 2014 Flow behavior around a square cylinder subject to modulation of a planar jet issued from upstream surface. J. Fluids Struct. 51, 362–383.Google Scholar
Igarashi, T. 1997 Drag reduction of a square prism by flow control using a small rod. J. Wind Engng Ind. Aerodyn. 69, 141–153.CrossRefGoogle Scholar
Kim, W., Yoo, J. Y. & Sung, J. 2006 Dynamics of vortex lock-on in a perturbed cylinder wake. Phys. Fluids 18 (7), 074103.CrossRefGoogle Scholar
Koutmos, P., Papailiou, D. & Bakrozis, A. 2004 Experimental and computational study of square cylinder wakes with two-dimensional injection into the base flow region. Eur. J. Mech. (B/Fluids) 23 (2), 353–365.Google Scholar
Kumar, R. A., Sohn, C. H. & Gowda, B. H. L. 2015 A PIV study of the near wake flow features of a square cylinder: influence of corner radius. J. Mech. Sci. Technol. 29 (2), 527–541.CrossRefGoogle Scholar
Ma, L. Q., Feng, L. H., Pan, C., Gao, Q. & Wang, J. J. 2015 Fourier mode decomposition of PIV data. Sci. China: Technol. Sci. 58 (11), 1935–1948.CrossRefGoogle Scholar
Meyer, K. E., Pedersen, J. M. & Özcan, O. 2007 A turbulent jet in crossflow analysed with proper orthogonal decomposition. J. Fluid Mech. 583, 199–227.Google Scholar
van Oudheusden, B. W., Scarano, F., van Hinsberg, N. P. & Watt, D. W. 2005 Phase-resolved characterization of vortex shedding in the near wake of a square-section cylinder at incidence. Exp. Fluids 39 (1), 86–98.CrossRefGoogle Scholar
Pan, C., Wang, H. P. & Wang, J. J. 2013 Phase identification of quasi-periodic flow measured by particle image velocimetry with a low sampling rate. Meas. Sci. Technol. 24 (5), 055305.CrossRefGoogle Scholar
Pan, C., Yu, D. S. & Wang, J. J. 2011 Dynamical mode decomposition of Gurney flap wake flow. Theor. Appl. Mech. Lett. 1 (1), 012002.CrossRefGoogle Scholar
Perrin, R., Braza, M., Cid, E., Cazin, S., Moradei, F., Barthet, A., Sevrain, A. & Hoarau, Y. 2006 Near-wake turbulence properties in the high Reynolds number incompressible flow around a circular cylinder measured by two-and three-component PIV. Flow Turbul. Combust. 77 (1–4), 185–204.CrossRefGoogle Scholar
Shao, C. P. & Wei, Q. D. 2008 Control of vortex shedding from a square cylinder. AIAA J. 46 (2), 397–407.Google Scholar
Shuster, J. M. & Smith, D. R. 2007 Experimental study of the formation and scaling of a round synthetic jet. Phys. Fluids 19, 045109.Google Scholar
Sirovich, L. 1987 Turbulence and the dynamics of coherent structures. Part I: coherent structures. Q. Appl. Maths 45 (3), 561–571.Google Scholar
Smith, B. L. & Glezer, A. 1998 The formation and evolution of synthetic jets. Phys. Fluids 10 (9), 2281–2297.Google Scholar
Tamura, T. & Miyagi, T. 1999 The effect of turbulence on aerodynamic forces on a square cylinder with various corner shapes. J. Wind Engng Ind. Aerodyn. 83 (1), 135–145.CrossRefGoogle Scholar
Tensi, J., Boué, I., Paillé, F. & Dury, G. 2002 Modification of the wake behind a circular cylinder by using synthetic jets. J. Vis. 5 (1), 37–44.Google Scholar
Ueda, Y., Kurata, M., Kida, T. & Iguchi, M. 2009 Visualization of flow past a square prism with cut-corners at the front-edge. J. Vis. 12 (4), 383–391.Google Scholar
Zhang, P. F., Wang, J. J. & Feng, L. H. 2008 Review of zero-net-mass-flux jet and its application in separation flow control. Sci. China E: Technol. Sci. 51 (9), 1315–1344.Google Scholar
Zhang, P. F., Wang, J. J., Lu, S. F. & Mi, J. 2005 Aerodynamic characteristics of a square cylinder with a rod in a staggered arrangement. Exp. Fluids 38 (4), 494–502.Google Scholar
Zhou, J., Adrian, R. J., Balachandar, S. & Kendall, T. M. 1999 Mechanisms for generating coherent packets of hairpin vortices in channel flow. J. Fluid Mech. 387, 353–396.CrossRefGoogle Scholar