1. Introduction
A weightless free drop attains a spherical equilibrium shape owing to surface tension and its inviscid natural frequencies obey the analytical Rayleigh–Lamb relation (Lamb Reference Lamb1924):
where the subscripts  $k$ and
$k$ and  $l$ are the poloidal and azimuthal wavenumbers,
$l$ are the poloidal and azimuthal wavenumbers,  $\sigma$ the surface tension,
$\sigma$ the surface tension,  $\rho$ the drop density and
$\rho$ the drop density and  $R$ its radius. It is noteworthy that the frequencies exhibit spectral degeneracy, indicating that different
$R$ its radius. It is noteworthy that the frequencies exhibit spectral degeneracy, indicating that different  $l \leq k$ modes (with
$l \leq k$ modes (with  $k > 0$) correspond to the same
$k > 0$) correspond to the same  $\lambda _{k,l}$. When the drop sits on a solid boundary, the contact line (CL) separating the immiscible fluids at the wall plays a key role as several mobility conditions are possible. In the special case of hemispherical drops with a free CL (fixed contact angle
$\lambda _{k,l}$. When the drop sits on a solid boundary, the contact line (CL) separating the immiscible fluids at the wall plays a key role as several mobility conditions are possible. In the special case of hemispherical drops with a free CL (fixed contact angle  $\alpha$; see figure 1), the frequency spectrum corresponds to the
$\alpha$; see figure 1), the frequency spectrum corresponds to the  $k + l=$ even subset of the spectrum (1.1). Indeed, the corresponding modes are mirror-symmetric about the equatorial plane, thus automatically satisfying the no-penetration condition at the solid surface. Although the spectral degeneracy of the free drop problem is carried over to the semi-drop, it can be broken by varying either the contact angle (Bostwick & Steen Reference Bostwick and Steen2014) or the CL mobility (Lyubimov, Lyubimova & Shklyaev Reference Lyubimov, Lyubimova and Shklyaev2006). Importantly, Bostwick & Steen (Reference Bostwick and Steen2014) extended the results of hemispherical drops to spherical-cap drops by using a Green's function method and the inverse operators for disturbances, which is solved through a Rayleigh–Ritz variational procedure. Within this framework, various CL conditions have been investigated, namely free and pinned (i.e. fixed CL) corresponding to lower and upper bounds on the natural frequencies. In addition, the linear dynamic condition (Davis–Hocking CL law) was seen to yield damped oscillations owing to a capillary dissipation at the CL. In the same work, it is also reported that the so-called Noether mode (
$k + l=$ even subset of the spectrum (1.1). Indeed, the corresponding modes are mirror-symmetric about the equatorial plane, thus automatically satisfying the no-penetration condition at the solid surface. Although the spectral degeneracy of the free drop problem is carried over to the semi-drop, it can be broken by varying either the contact angle (Bostwick & Steen Reference Bostwick and Steen2014) or the CL mobility (Lyubimov, Lyubimova & Shklyaev Reference Lyubimov, Lyubimova and Shklyaev2006). Importantly, Bostwick & Steen (Reference Bostwick and Steen2014) extended the results of hemispherical drops to spherical-cap drops by using a Green's function method and the inverse operators for disturbances, which is solved through a Rayleigh–Ritz variational procedure. Within this framework, various CL conditions have been investigated, namely free and pinned (i.e. fixed CL) corresponding to lower and upper bounds on the natural frequencies. In addition, the linear dynamic condition (Davis–Hocking CL law) was seen to yield damped oscillations owing to a capillary dissipation at the CL. In the same work, it is also reported that the so-called Noether mode ( $k=l=1$) with free CL becomes unstable for super-hemispherical base states (i.e. static contact angle
$k=l=1$) with free CL becomes unstable for super-hemispherical base states (i.e. static contact angle  $90^{\circ} < \alpha < 180^{\circ }$). This instability corresponds to a spontaneous horizontal motion of the centre of mass, called the ’walking’ instability, which is also discussed in the following.
$90^{\circ} < \alpha < 180^{\circ }$). This instability corresponds to a spontaneous horizontal motion of the centre of mass, called the ’walking’ instability, which is also discussed in the following.
As the drop shape differs from that of the spherical cap, however, there are no general theoretical models for the natural frequencies, owing to the difficulties in the geometrical treatment of the flattened drop configuration and the motion of the three-phase CL. Thus, the effect of gravity on the natural frequencies and the corresponding modes of a sessile drop had not been tackled until the recent paper of Zhang, Zhou & Ding (Reference Zhang, Zhou and Ding2023), where the corresponding eigenvalue problem is solved numerically through a general boundary element method (BEM) for different Bond numbers, CL conditions (either free or pinned) and static equilibrium contact angle.
2. Overview
Consider a sessile drop sitting on a plane under the influence of gravity with static contact angle  $\alpha$ (see figure 1a). The fluid is assumed to be incompressible and irrotational, and hence the velocity field can be written as
$\alpha$ (see figure 1a). The fluid is assumed to be incompressible and irrotational, and hence the velocity field can be written as  $\boldsymbol {u}= - \boldsymbol {\nabla } \psi$ and conservation of mass reduces to the Laplace equation for the potential,
$\boldsymbol {u}= - \boldsymbol {\nabla } \psi$ and conservation of mass reduces to the Laplace equation for the potential,  $\nabla ^2 \psi =0$. On the free surface, the fluid velocity component perpendicular to the interface has to match that of the interface itself (kinematic condition) which, in the limit of small amplitudes, reads
$\nabla ^2 \psi =0$. On the free surface, the fluid velocity component perpendicular to the interface has to match that of the interface itself (kinematic condition) which, in the limit of small amplitudes, reads  $\boldsymbol {n} \boldsymbol {\cdot } \boldsymbol {\nabla } \psi =-({\partial \eta }/{\partial t})$, where
$\boldsymbol {n} \boldsymbol {\cdot } \boldsymbol {\nabla } \psi =-({\partial \eta }/{\partial t})$, where  $\boldsymbol {n}$ is the normal unit vector pointing out of the fluid domain and
$\boldsymbol {n}$ is the normal unit vector pointing out of the fluid domain and  $\eta$ is the perturbation of the free surface, satisfying the condition of volume conservation. The Young–Laplace equation, relating the mean curvature and the pressure difference across the free surface, is then combined with the linearized Bernoulli equation:
$\eta$ is the perturbation of the free surface, satisfying the condition of volume conservation. The Young–Laplace equation, relating the mean curvature and the pressure difference across the free surface, is then combined with the linearized Bernoulli equation:
Here  $\Delta _\varGamma$ is the Laplace–Beltrami operator depending on the equilibrium shape
$\Delta _\varGamma$ is the Laplace–Beltrami operator depending on the equilibrium shape  $\varGamma$,
$\varGamma$,  $(k_1,k_2)$ are the two principal curvatures of
$(k_1,k_2)$ are the two principal curvatures of  $\varGamma$ and
$\varGamma$ and  $\varPi =g z$ is the gravitational potential. On the solid surface the no-penetration condition is enforced, while at the CL a phenomenological condition must be imposed. The linear condition
$\varPi =g z$ is the gravitational potential. On the solid surface the no-penetration condition is enforced, while at the CL a phenomenological condition must be imposed. The linear condition  $\boldsymbol {e} \boldsymbol {\cdot } \boldsymbol {\nabla } \eta + \chi \eta =0$ is compatible with the stability analysis (see figure 1a, where
$\boldsymbol {e} \boldsymbol {\cdot } \boldsymbol {\nabla } \eta + \chi \eta =0$ is compatible with the stability analysis (see figure 1a, where  $\boldsymbol {e}$ is the tangent unit vector), with the mobility parameter given by
$\boldsymbol {e}$ is the tangent unit vector), with the mobility parameter given by  $\chi =k_1(s_c) \cot \alpha$ or
$\chi =k_1(s_c) \cot \alpha$ or  $\chi \rightarrow \infty$ for free and pinned conditions, respectively. The system of governing equations, free-surface and CL conditions can be turned into an eigenvalue problem through the normal mode expansion
$\chi \rightarrow \infty$ for free and pinned conditions, respectively. The system of governing equations, free-surface and CL conditions can be turned into an eigenvalue problem through the normal mode expansion  $\psi (\boldsymbol {x},t)=\phi (r,z){\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$ and
$\psi (\boldsymbol {x},t)=\phi (r,z){\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$ and  $\eta (s,\varphi,t)=y(s) {\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$, where
$\eta (s,\varphi,t)=y(s) {\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$, where  $\lambda$ is the unknown complex eigenvalue.
$\lambda$ is the unknown complex eigenvalue.
Zhang et al. (Reference Zhang, Zhou and Ding2023) tackle such a problem through a BEM, which can deal with arbitrary drop geometry, with the advantage of reducing the two-dimensional problem to a boundary integral equation. The modes are then classified by the pair  $\{n,l\}$, where the latter is the azimuthal wavenumber and the former indicates the number of vertical layers of the perturbation, which is related to the polar wavenumber of spherical harmonics introduced in (1.1) as
$\{n,l\}$, where the latter is the azimuthal wavenumber and the former indicates the number of vertical layers of the perturbation, which is related to the polar wavenumber of spherical harmonics introduced in (1.1) as  $n=(k-l)/2+1$. Figure 1(b) shows the first zonal (axisymmetric,
$n=(k-l)/2+1$. Figure 1(b) shows the first zonal (axisymmetric,  $\{n > 1,l = 0\}$), sectoral (star-shaped,
$\{n > 1,l = 0\}$), sectoral (star-shaped,  $\{n = 1,l \geq 1\}$) and tesseral (
$\{n = 1,l \geq 1\}$) and tesseral ( $\{n > 1, l \geq 1 \}$) modes. The key contribution of the paper by Zhang et al. (Reference Zhang, Zhou and Ding2023) lies in a systematic investigation of the effects of gravity on the axisymmetric and non-axisymmetric oscillations of sessile drops over a wide range of static contact angles
$\{n > 1, l \geq 1 \}$) modes. The key contribution of the paper by Zhang et al. (Reference Zhang, Zhou and Ding2023) lies in a systematic investigation of the effects of gravity on the axisymmetric and non-axisymmetric oscillations of sessile drops over a wide range of static contact angles  $\alpha \in [30^{\circ }\unicode{x2013}150^{\circ }]$ and Bond numbers
$\alpha \in [30^{\circ }\unicode{x2013}150^{\circ }]$ and Bond numbers  $Bo =\rho g l_*^2 /\sigma \in [0\unicode{x2013}10]$, with the characteristic length scale
$Bo =\rho g l_*^2 /\sigma \in [0\unicode{x2013}10]$, with the characteristic length scale  $l_*=[3 \tilde {v}/(2 {\rm \pi})]^{1/3}$ based on the the drop volume
$l_*=[3 \tilde {v}/(2 {\rm \pi})]^{1/3}$ based on the the drop volume  $\tilde {v}$. It is shown that the frequency of zonal modes decreases with gravity at small contact angle, but increases when the contact angle exceeds a certain critical value, with larger
$\tilde {v}$. It is shown that the frequency of zonal modes decreases with gravity at small contact angle, but increases when the contact angle exceeds a certain critical value, with larger  $\alpha$ being more sensitive to the effects of gravity (in agreement with the numerical simulations of Sakakeeny & Ling (Reference Sakakeeny and Ling2021)). The modes with free CL have a larger frequency shift than the corresponding pinned modes, especially at low
$\alpha$ being more sensitive to the effects of gravity (in agreement with the numerical simulations of Sakakeeny & Ling (Reference Sakakeeny and Ling2021)). The modes with free CL have a larger frequency shift than the corresponding pinned modes, especially at low  $n$. In contrast, most of the sectoral modes show a significant frequency decrease for all contact angles in the presence of gravity. The downward frequency shifts for pinned CL are smaller than for free conditions, whereas upward frequency shifts occur for pinned CL and large
$n$. In contrast, most of the sectoral modes show a significant frequency decrease for all contact angles in the presence of gravity. The downward frequency shifts for pinned CL are smaller than for free conditions, whereas upward frequency shifts occur for pinned CL and large  $\alpha$, only. In the presence of gravity, the frequencies of most tesseral modes decrease at small contact angles and increase at large ones (similarly to zonal modes), although some modes with small
$\alpha$, only. In the presence of gravity, the frequencies of most tesseral modes decrease at small contact angles and increase at large ones (similarly to zonal modes), although some modes with small  $n$ and large
$n$ and large  $l$ manifest a frequency decrease at small
$l$ manifest a frequency decrease at small  $\alpha$ (as happens for sectoral modes). This analysis highlights that the spectral degeneracy of hemispherical drops (
$\alpha$ (as happens for sectoral modes). This analysis highlights that the spectral degeneracy of hemispherical drops ( $\alpha =90 ^{\circ }$) inherited from the Rayleigh–Lamb spectrum (1.1) is also broken by gravity, with lower (higher) frequencies for higher (lower) azimuthal wavenumber
$\alpha =90 ^{\circ }$) inherited from the Rayleigh–Lamb spectrum (1.1) is also broken by gravity, with lower (higher) frequencies for higher (lower) azimuthal wavenumber  $l$ with respect to the
$l$ with respect to the  $Bo=0$ case.
$Bo=0$ case.
In the absence of gravity and with free CL conditions, the lowest non-zero frequency mode (which is of particular interest as it is expected to be the dominant mode) corresponds to the zonal mode  $\{2, 0\}$ for
$\{2, 0\}$ for  $\alpha > 90 ^{\circ }$ and to the sectoral mode
$\alpha > 90 ^{\circ }$ and to the sectoral mode  $\{1, 2\}$ for
$\{1, 2\}$ for  $\alpha < 90 ^{\circ }$. Conversely, as
$\alpha < 90 ^{\circ }$. Conversely, as  $Bo$ increases, it is found that the lowest mode of a drop with
$Bo$ increases, it is found that the lowest mode of a drop with  $\alpha > 90 ^{\circ }$ gradually switches from mode
$\alpha > 90 ^{\circ }$ gradually switches from mode  $\{2, 0\}$ to
$\{2, 0\}$ to  $\{1, 2\}$, with the consequence that for sufficiently high
$\{1, 2\}$, with the consequence that for sufficiently high  $Bo$ the mode
$Bo$ the mode  $\{1, 2\}$ is the lowest mode regardless of the contact angle. As observed by Zhang et al. (Reference Zhang, Zhou and Ding2023), this result implies that for large drops (and movable CL), non-axisymmetric oscillation will more likely manifest in large drops than in smaller ones.
$\{1, 2\}$ is the lowest mode regardless of the contact angle. As observed by Zhang et al. (Reference Zhang, Zhou and Ding2023), this result implies that for large drops (and movable CL), non-axisymmetric oscillation will more likely manifest in large drops than in smaller ones.
Ultimately, one of the main points of the paper is that the frequency of the Noether mode  $\{1, 1\}$ with free CL conditions is the only frequency that is not shifted by gravity and is always zero regardless of
$\{1, 1\}$ with free CL conditions is the only frequency that is not shifted by gravity and is always zero regardless of  $\alpha$ and
$\alpha$ and  $Bo$. This finding is obtained numerically and confirmed by static stability theory, thus implying that the walking drop instability (Bostwick & Steen Reference Bostwick and Steen2014) seems not to be present and an additional surface energy gradient is needed in order to break the horizontal translational invariance of the drop.
$Bo$. This finding is obtained numerically and confirmed by static stability theory, thus implying that the walking drop instability (Bostwick & Steen Reference Bostwick and Steen2014) seems not to be present and an additional surface energy gradient is needed in order to break the horizontal translational invariance of the drop.
3. Future
The appeal of the approach by Zhang et al. (Reference Zhang, Zhou and Ding2023) comes from the effectiveness in solving the small-amplitude dynamics of inviscid drops of arbitrary shape. These results can be of valuable help in several applications, including inkjet printing, additive manufacturing, printed electronic components and circuits, forensic bloodstains, colloidal aggregation and biological flows such as plants transpiration, among many others. A direct continuation of the work could involve the investigation of other constrained capillary surfaces, such as liquid bridges or drops on fibres, where theoretical predictions are lacking, especially when gravity plays a role.
Looking ahead, the results by Zhang et al. (Reference Zhang, Zhou and Ding2023) are limited to the case of free or pinned CL, whereas its motion is expected to greatly affect the dynamics of the perturbation. The dynamic CL condition could be investigated in a linear setting resorting to a contact angle deviation proportional to the CL speed  $\Delta \alpha = \varLambda u_{CL}$, where the free and pinned conditions are retrieved for the limiting case of the mobility parameter
$\Delta \alpha = \varLambda u_{CL}$, where the free and pinned conditions are retrieved for the limiting case of the mobility parameter  $\varLambda =0$ and
$\varLambda =0$ and  $\varLambda \rightarrow \infty$, respectively. Such a simple CL condition (referred to as the Davis–Hocking condition) has already been applied to hemispherical (Lyubimov et al. Reference Lyubimov, Lyubimova and Shklyaev2006) and spherical-cap (Bostwick & Steen Reference Bostwick and Steen2014) drops since it is compatible with the eigenvalue problem introduced above and can be incorporated in the BEM. Yet, experimental observations point to a nonlinear relation between CL velocity and contact angle, which prevents the formulation of an eigenvalue approach. Nonetheless, the linear modes of Zhang et al. (Reference Zhang, Zhou and Ding2023) can be used as a first-order solution of an asymptotic expansion to incorporate a nonlinear CL law, as proposed by Viola, Brun & Gallaire (Reference Viola, Brun and Gallaire2018) where the stick–slip CL dynamics of inviscid sloshing waves subjected contact angle hysteresis is solved through of a weakly nonlinear analysis. A similar contact angle model has been also used (Ludwicki et al. Reference Ludwicki, Kern, McCraney, Bostwick, Daniel and Steen2022) to investigate numerically the coalescence of sessile drops using a three-dimensional volume-of-fluid method to track the motion of the free surface. Alternatively, an immersed boundary approach can be exploited to account for viscous, convective and buoyancy effects on sessile drops, along with their collective dynamics as done by Chong et al. (Reference Chong, Li, Ng, Verzicco and Lohse2020).
$\varLambda \rightarrow \infty$, respectively. Such a simple CL condition (referred to as the Davis–Hocking condition) has already been applied to hemispherical (Lyubimov et al. Reference Lyubimov, Lyubimova and Shklyaev2006) and spherical-cap (Bostwick & Steen Reference Bostwick and Steen2014) drops since it is compatible with the eigenvalue problem introduced above and can be incorporated in the BEM. Yet, experimental observations point to a nonlinear relation between CL velocity and contact angle, which prevents the formulation of an eigenvalue approach. Nonetheless, the linear modes of Zhang et al. (Reference Zhang, Zhou and Ding2023) can be used as a first-order solution of an asymptotic expansion to incorporate a nonlinear CL law, as proposed by Viola, Brun & Gallaire (Reference Viola, Brun and Gallaire2018) where the stick–slip CL dynamics of inviscid sloshing waves subjected contact angle hysteresis is solved through of a weakly nonlinear analysis. A similar contact angle model has been also used (Ludwicki et al. Reference Ludwicki, Kern, McCraney, Bostwick, Daniel and Steen2022) to investigate numerically the coalescence of sessile drops using a three-dimensional volume-of-fluid method to track the motion of the free surface. Alternatively, an immersed boundary approach can be exploited to account for viscous, convective and buoyancy effects on sessile drops, along with their collective dynamics as done by Chong et al. (Reference Chong, Li, Ng, Verzicco and Lohse2020).
The findings of Zhang et al. (Reference Zhang, Zhou and Ding2023) shed new light on the effects of gravity on sessile drop oscillations, which deserve to be further investigated experimentally. Specifically, the frequency spectrum shift produced by gravity is seen to be sensitive to the contact angle and to the azimuthal wavenumber; comprehensive experimental studies of this aspect for high-order and non-axisymmetric modes are still lacking and they would be very welcome to complete the picture.
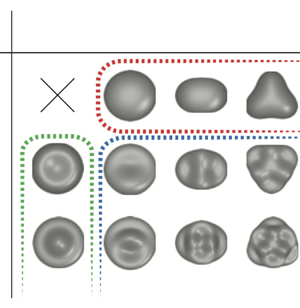

 $\bar {\varGamma }$ and unperturbed
$\bar {\varGamma }$ and unperturbed  $\varGamma$ surface of a drop with static contact angle
$\varGamma$ surface of a drop with static contact angle  $\alpha$ with a curvilinear coordinate
$\alpha$ with a curvilinear coordinate  $s$ (
$s$ ( $s=s_c$ corresponds to the CL position) and Frenet frame
$s=s_c$ corresponds to the CL position) and Frenet frame  $(\boldsymbol {e},\boldsymbol {n})$. (b) Mode shapes of a sessile drop with
$(\boldsymbol {e},\boldsymbol {n})$. (b) Mode shapes of a sessile drop with  $\alpha = 90^{\circ }$ and
$\alpha = 90^{\circ }$ and  $Bo=5$ for free CL condition. Adapted from Zhang et al. (2023).
$Bo=5$ for free CL condition. Adapted from Zhang et al. (2023).


1. Introduction
A weightless free drop attains a spherical equilibrium shape owing to surface tension and its inviscid natural frequencies obey the analytical Rayleigh–Lamb relation (Lamb Reference Lamb1924):
where the subscripts $k$ and
$k$ and  $l$ are the poloidal and azimuthal wavenumbers,
$l$ are the poloidal and azimuthal wavenumbers,  $\sigma$ the surface tension,
$\sigma$ the surface tension,  $\rho$ the drop density and
$\rho$ the drop density and  $R$ its radius. It is noteworthy that the frequencies exhibit spectral degeneracy, indicating that different
$R$ its radius. It is noteworthy that the frequencies exhibit spectral degeneracy, indicating that different  $l \leq k$ modes (with
$l \leq k$ modes (with  $k > 0$) correspond to the same
$k > 0$) correspond to the same  $\lambda _{k,l}$. When the drop sits on a solid boundary, the contact line (CL) separating the immiscible fluids at the wall plays a key role as several mobility conditions are possible. In the special case of hemispherical drops with a free CL (fixed contact angle
$\lambda _{k,l}$. When the drop sits on a solid boundary, the contact line (CL) separating the immiscible fluids at the wall plays a key role as several mobility conditions are possible. In the special case of hemispherical drops with a free CL (fixed contact angle  $\alpha$; see figure 1), the frequency spectrum corresponds to the
$\alpha$; see figure 1), the frequency spectrum corresponds to the  $k + l=$ even subset of the spectrum (1.1). Indeed, the corresponding modes are mirror-symmetric about the equatorial plane, thus automatically satisfying the no-penetration condition at the solid surface. Although the spectral degeneracy of the free drop problem is carried over to the semi-drop, it can be broken by varying either the contact angle (Bostwick & Steen Reference Bostwick and Steen2014) or the CL mobility (Lyubimov, Lyubimova & Shklyaev Reference Lyubimov, Lyubimova and Shklyaev2006). Importantly, Bostwick & Steen (Reference Bostwick and Steen2014) extended the results of hemispherical drops to spherical-cap drops by using a Green's function method and the inverse operators for disturbances, which is solved through a Rayleigh–Ritz variational procedure. Within this framework, various CL conditions have been investigated, namely free and pinned (i.e. fixed CL) corresponding to lower and upper bounds on the natural frequencies. In addition, the linear dynamic condition (Davis–Hocking CL law) was seen to yield damped oscillations owing to a capillary dissipation at the CL. In the same work, it is also reported that the so-called Noether mode (
$k + l=$ even subset of the spectrum (1.1). Indeed, the corresponding modes are mirror-symmetric about the equatorial plane, thus automatically satisfying the no-penetration condition at the solid surface. Although the spectral degeneracy of the free drop problem is carried over to the semi-drop, it can be broken by varying either the contact angle (Bostwick & Steen Reference Bostwick and Steen2014) or the CL mobility (Lyubimov, Lyubimova & Shklyaev Reference Lyubimov, Lyubimova and Shklyaev2006). Importantly, Bostwick & Steen (Reference Bostwick and Steen2014) extended the results of hemispherical drops to spherical-cap drops by using a Green's function method and the inverse operators for disturbances, which is solved through a Rayleigh–Ritz variational procedure. Within this framework, various CL conditions have been investigated, namely free and pinned (i.e. fixed CL) corresponding to lower and upper bounds on the natural frequencies. In addition, the linear dynamic condition (Davis–Hocking CL law) was seen to yield damped oscillations owing to a capillary dissipation at the CL. In the same work, it is also reported that the so-called Noether mode ( $k=l=1$) with free CL becomes unstable for super-hemispherical base states (i.e. static contact angle
$k=l=1$) with free CL becomes unstable for super-hemispherical base states (i.e. static contact angle  $90^{\circ} < \alpha < 180^{\circ }$). This instability corresponds to a spontaneous horizontal motion of the centre of mass, called the ’walking’ instability, which is also discussed in the following.
$90^{\circ} < \alpha < 180^{\circ }$). This instability corresponds to a spontaneous horizontal motion of the centre of mass, called the ’walking’ instability, which is also discussed in the following.
Figure 1. (a) Perturbed $\bar {\varGamma }$ and unperturbed
$\bar {\varGamma }$ and unperturbed  $\varGamma$ surface of a drop with static contact angle
$\varGamma$ surface of a drop with static contact angle  $\alpha$ with a curvilinear coordinate
$\alpha$ with a curvilinear coordinate  $s$ (
$s$ ( $s=s_c$ corresponds to the CL position) and Frenet frame
$s=s_c$ corresponds to the CL position) and Frenet frame  $(\boldsymbol {e},\boldsymbol {n})$. (b) Mode shapes of a sessile drop with
$(\boldsymbol {e},\boldsymbol {n})$. (b) Mode shapes of a sessile drop with  $\alpha = 90^{\circ }$ and
$\alpha = 90^{\circ }$ and  $Bo=5$ for free CL condition. Adapted from Zhang et al. (Reference Zhang, Zhou and Ding2023).
$Bo=5$ for free CL condition. Adapted from Zhang et al. (Reference Zhang, Zhou and Ding2023).
As the drop shape differs from that of the spherical cap, however, there are no general theoretical models for the natural frequencies, owing to the difficulties in the geometrical treatment of the flattened drop configuration and the motion of the three-phase CL. Thus, the effect of gravity on the natural frequencies and the corresponding modes of a sessile drop had not been tackled until the recent paper of Zhang, Zhou & Ding (Reference Zhang, Zhou and Ding2023), where the corresponding eigenvalue problem is solved numerically through a general boundary element method (BEM) for different Bond numbers, CL conditions (either free or pinned) and static equilibrium contact angle.
2. Overview
Consider a sessile drop sitting on a plane under the influence of gravity with static contact angle $\alpha$ (see figure 1a). The fluid is assumed to be incompressible and irrotational, and hence the velocity field can be written as
$\alpha$ (see figure 1a). The fluid is assumed to be incompressible and irrotational, and hence the velocity field can be written as  $\boldsymbol {u}= - \boldsymbol {\nabla } \psi$ and conservation of mass reduces to the Laplace equation for the potential,
$\boldsymbol {u}= - \boldsymbol {\nabla } \psi$ and conservation of mass reduces to the Laplace equation for the potential,  $\nabla ^2 \psi =0$. On the free surface, the fluid velocity component perpendicular to the interface has to match that of the interface itself (kinematic condition) which, in the limit of small amplitudes, reads
$\nabla ^2 \psi =0$. On the free surface, the fluid velocity component perpendicular to the interface has to match that of the interface itself (kinematic condition) which, in the limit of small amplitudes, reads  $\boldsymbol {n} \boldsymbol {\cdot } \boldsymbol {\nabla } \psi =-({\partial \eta }/{\partial t})$, where
$\boldsymbol {n} \boldsymbol {\cdot } \boldsymbol {\nabla } \psi =-({\partial \eta }/{\partial t})$, where  $\boldsymbol {n}$ is the normal unit vector pointing out of the fluid domain and
$\boldsymbol {n}$ is the normal unit vector pointing out of the fluid domain and  $\eta$ is the perturbation of the free surface, satisfying the condition of volume conservation. The Young–Laplace equation, relating the mean curvature and the pressure difference across the free surface, is then combined with the linearized Bernoulli equation:
$\eta$ is the perturbation of the free surface, satisfying the condition of volume conservation. The Young–Laplace equation, relating the mean curvature and the pressure difference across the free surface, is then combined with the linearized Bernoulli equation:
Here $\Delta _\varGamma$ is the Laplace–Beltrami operator depending on the equilibrium shape
$\Delta _\varGamma$ is the Laplace–Beltrami operator depending on the equilibrium shape  $\varGamma$,
$\varGamma$,  $(k_1,k_2)$ are the two principal curvatures of
$(k_1,k_2)$ are the two principal curvatures of  $\varGamma$ and
$\varGamma$ and  $\varPi =g z$ is the gravitational potential. On the solid surface the no-penetration condition is enforced, while at the CL a phenomenological condition must be imposed. The linear condition
$\varPi =g z$ is the gravitational potential. On the solid surface the no-penetration condition is enforced, while at the CL a phenomenological condition must be imposed. The linear condition  $\boldsymbol {e} \boldsymbol {\cdot } \boldsymbol {\nabla } \eta + \chi \eta =0$ is compatible with the stability analysis (see figure 1a, where
$\boldsymbol {e} \boldsymbol {\cdot } \boldsymbol {\nabla } \eta + \chi \eta =0$ is compatible with the stability analysis (see figure 1a, where  $\boldsymbol {e}$ is the tangent unit vector), with the mobility parameter given by
$\boldsymbol {e}$ is the tangent unit vector), with the mobility parameter given by  $\chi =k_1(s_c) \cot \alpha$ or
$\chi =k_1(s_c) \cot \alpha$ or  $\chi \rightarrow \infty$ for free and pinned conditions, respectively. The system of governing equations, free-surface and CL conditions can be turned into an eigenvalue problem through the normal mode expansion
$\chi \rightarrow \infty$ for free and pinned conditions, respectively. The system of governing equations, free-surface and CL conditions can be turned into an eigenvalue problem through the normal mode expansion  $\psi (\boldsymbol {x},t)=\phi (r,z){\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$ and
$\psi (\boldsymbol {x},t)=\phi (r,z){\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$ and  $\eta (s,\varphi,t)=y(s) {\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$, where
$\eta (s,\varphi,t)=y(s) {\rm e}^{{\rm i} \lambda t} {\rm e}^{{\rm i} l \varphi }$, where  $\lambda$ is the unknown complex eigenvalue.
$\lambda$ is the unknown complex eigenvalue.
Zhang et al. (Reference Zhang, Zhou and Ding2023) tackle such a problem through a BEM, which can deal with arbitrary drop geometry, with the advantage of reducing the two-dimensional problem to a boundary integral equation. The modes are then classified by the pair $\{n,l\}$, where the latter is the azimuthal wavenumber and the former indicates the number of vertical layers of the perturbation, which is related to the polar wavenumber of spherical harmonics introduced in (1.1) as
$\{n,l\}$, where the latter is the azimuthal wavenumber and the former indicates the number of vertical layers of the perturbation, which is related to the polar wavenumber of spherical harmonics introduced in (1.1) as  $n=(k-l)/2+1$. Figure 1(b) shows the first zonal (axisymmetric,
$n=(k-l)/2+1$. Figure 1(b) shows the first zonal (axisymmetric,  $\{n > 1,l = 0\}$), sectoral (star-shaped,
$\{n > 1,l = 0\}$), sectoral (star-shaped,  $\{n = 1,l \geq 1\}$) and tesseral (
$\{n = 1,l \geq 1\}$) and tesseral ( $\{n > 1, l \geq 1 \}$) modes. The key contribution of the paper by Zhang et al. (Reference Zhang, Zhou and Ding2023) lies in a systematic investigation of the effects of gravity on the axisymmetric and non-axisymmetric oscillations of sessile drops over a wide range of static contact angles
$\{n > 1, l \geq 1 \}$) modes. The key contribution of the paper by Zhang et al. (Reference Zhang, Zhou and Ding2023) lies in a systematic investigation of the effects of gravity on the axisymmetric and non-axisymmetric oscillations of sessile drops over a wide range of static contact angles  $\alpha \in [30^{\circ }\unicode{x2013}150^{\circ }]$ and Bond numbers
$\alpha \in [30^{\circ }\unicode{x2013}150^{\circ }]$ and Bond numbers  $Bo =\rho g l_*^2 /\sigma \in [0\unicode{x2013}10]$, with the characteristic length scale
$Bo =\rho g l_*^2 /\sigma \in [0\unicode{x2013}10]$, with the characteristic length scale  $l_*=[3 \tilde {v}/(2 {\rm \pi})]^{1/3}$ based on the the drop volume
$l_*=[3 \tilde {v}/(2 {\rm \pi})]^{1/3}$ based on the the drop volume  $\tilde {v}$. It is shown that the frequency of zonal modes decreases with gravity at small contact angle, but increases when the contact angle exceeds a certain critical value, with larger
$\tilde {v}$. It is shown that the frequency of zonal modes decreases with gravity at small contact angle, but increases when the contact angle exceeds a certain critical value, with larger  $\alpha$ being more sensitive to the effects of gravity (in agreement with the numerical simulations of Sakakeeny & Ling (Reference Sakakeeny and Ling2021)). The modes with free CL have a larger frequency shift than the corresponding pinned modes, especially at low
$\alpha$ being more sensitive to the effects of gravity (in agreement with the numerical simulations of Sakakeeny & Ling (Reference Sakakeeny and Ling2021)). The modes with free CL have a larger frequency shift than the corresponding pinned modes, especially at low  $n$. In contrast, most of the sectoral modes show a significant frequency decrease for all contact angles in the presence of gravity. The downward frequency shifts for pinned CL are smaller than for free conditions, whereas upward frequency shifts occur for pinned CL and large
$n$. In contrast, most of the sectoral modes show a significant frequency decrease for all contact angles in the presence of gravity. The downward frequency shifts for pinned CL are smaller than for free conditions, whereas upward frequency shifts occur for pinned CL and large  $\alpha$, only. In the presence of gravity, the frequencies of most tesseral modes decrease at small contact angles and increase at large ones (similarly to zonal modes), although some modes with small
$\alpha$, only. In the presence of gravity, the frequencies of most tesseral modes decrease at small contact angles and increase at large ones (similarly to zonal modes), although some modes with small  $n$ and large
$n$ and large  $l$ manifest a frequency decrease at small
$l$ manifest a frequency decrease at small  $\alpha$ (as happens for sectoral modes). This analysis highlights that the spectral degeneracy of hemispherical drops (
$\alpha$ (as happens for sectoral modes). This analysis highlights that the spectral degeneracy of hemispherical drops ( $\alpha =90 ^{\circ }$) inherited from the Rayleigh–Lamb spectrum (1.1) is also broken by gravity, with lower (higher) frequencies for higher (lower) azimuthal wavenumber
$\alpha =90 ^{\circ }$) inherited from the Rayleigh–Lamb spectrum (1.1) is also broken by gravity, with lower (higher) frequencies for higher (lower) azimuthal wavenumber  $l$ with respect to the
$l$ with respect to the  $Bo=0$ case.
$Bo=0$ case.
In the absence of gravity and with free CL conditions, the lowest non-zero frequency mode (which is of particular interest as it is expected to be the dominant mode) corresponds to the zonal mode $\{2, 0\}$ for
$\{2, 0\}$ for  $\alpha > 90 ^{\circ }$ and to the sectoral mode
$\alpha > 90 ^{\circ }$ and to the sectoral mode  $\{1, 2\}$ for
$\{1, 2\}$ for  $\alpha < 90 ^{\circ }$. Conversely, as
$\alpha < 90 ^{\circ }$. Conversely, as  $Bo$ increases, it is found that the lowest mode of a drop with
$Bo$ increases, it is found that the lowest mode of a drop with  $\alpha > 90 ^{\circ }$ gradually switches from mode
$\alpha > 90 ^{\circ }$ gradually switches from mode  $\{2, 0\}$ to
$\{2, 0\}$ to  $\{1, 2\}$, with the consequence that for sufficiently high
$\{1, 2\}$, with the consequence that for sufficiently high  $Bo$ the mode
$Bo$ the mode  $\{1, 2\}$ is the lowest mode regardless of the contact angle. As observed by Zhang et al. (Reference Zhang, Zhou and Ding2023), this result implies that for large drops (and movable CL), non-axisymmetric oscillation will more likely manifest in large drops than in smaller ones.
$\{1, 2\}$ is the lowest mode regardless of the contact angle. As observed by Zhang et al. (Reference Zhang, Zhou and Ding2023), this result implies that for large drops (and movable CL), non-axisymmetric oscillation will more likely manifest in large drops than in smaller ones.
Ultimately, one of the main points of the paper is that the frequency of the Noether mode $\{1, 1\}$ with free CL conditions is the only frequency that is not shifted by gravity and is always zero regardless of
$\{1, 1\}$ with free CL conditions is the only frequency that is not shifted by gravity and is always zero regardless of  $\alpha$ and
$\alpha$ and  $Bo$. This finding is obtained numerically and confirmed by static stability theory, thus implying that the walking drop instability (Bostwick & Steen Reference Bostwick and Steen2014) seems not to be present and an additional surface energy gradient is needed in order to break the horizontal translational invariance of the drop.
$Bo$. This finding is obtained numerically and confirmed by static stability theory, thus implying that the walking drop instability (Bostwick & Steen Reference Bostwick and Steen2014) seems not to be present and an additional surface energy gradient is needed in order to break the horizontal translational invariance of the drop.
3. Future
The appeal of the approach by Zhang et al. (Reference Zhang, Zhou and Ding2023) comes from the effectiveness in solving the small-amplitude dynamics of inviscid drops of arbitrary shape. These results can be of valuable help in several applications, including inkjet printing, additive manufacturing, printed electronic components and circuits, forensic bloodstains, colloidal aggregation and biological flows such as plants transpiration, among many others. A direct continuation of the work could involve the investigation of other constrained capillary surfaces, such as liquid bridges or drops on fibres, where theoretical predictions are lacking, especially when gravity plays a role.
Looking ahead, the results by Zhang et al. (Reference Zhang, Zhou and Ding2023) are limited to the case of free or pinned CL, whereas its motion is expected to greatly affect the dynamics of the perturbation. The dynamic CL condition could be investigated in a linear setting resorting to a contact angle deviation proportional to the CL speed $\Delta \alpha = \varLambda u_{CL}$, where the free and pinned conditions are retrieved for the limiting case of the mobility parameter
$\Delta \alpha = \varLambda u_{CL}$, where the free and pinned conditions are retrieved for the limiting case of the mobility parameter  $\varLambda =0$ and
$\varLambda =0$ and  $\varLambda \rightarrow \infty$, respectively. Such a simple CL condition (referred to as the Davis–Hocking condition) has already been applied to hemispherical (Lyubimov et al. Reference Lyubimov, Lyubimova and Shklyaev2006) and spherical-cap (Bostwick & Steen Reference Bostwick and Steen2014) drops since it is compatible with the eigenvalue problem introduced above and can be incorporated in the BEM. Yet, experimental observations point to a nonlinear relation between CL velocity and contact angle, which prevents the formulation of an eigenvalue approach. Nonetheless, the linear modes of Zhang et al. (Reference Zhang, Zhou and Ding2023) can be used as a first-order solution of an asymptotic expansion to incorporate a nonlinear CL law, as proposed by Viola, Brun & Gallaire (Reference Viola, Brun and Gallaire2018) where the stick–slip CL dynamics of inviscid sloshing waves subjected contact angle hysteresis is solved through of a weakly nonlinear analysis. A similar contact angle model has been also used (Ludwicki et al. Reference Ludwicki, Kern, McCraney, Bostwick, Daniel and Steen2022) to investigate numerically the coalescence of sessile drops using a three-dimensional volume-of-fluid method to track the motion of the free surface. Alternatively, an immersed boundary approach can be exploited to account for viscous, convective and buoyancy effects on sessile drops, along with their collective dynamics as done by Chong et al. (Reference Chong, Li, Ng, Verzicco and Lohse2020).
$\varLambda \rightarrow \infty$, respectively. Such a simple CL condition (referred to as the Davis–Hocking condition) has already been applied to hemispherical (Lyubimov et al. Reference Lyubimov, Lyubimova and Shklyaev2006) and spherical-cap (Bostwick & Steen Reference Bostwick and Steen2014) drops since it is compatible with the eigenvalue problem introduced above and can be incorporated in the BEM. Yet, experimental observations point to a nonlinear relation between CL velocity and contact angle, which prevents the formulation of an eigenvalue approach. Nonetheless, the linear modes of Zhang et al. (Reference Zhang, Zhou and Ding2023) can be used as a first-order solution of an asymptotic expansion to incorporate a nonlinear CL law, as proposed by Viola, Brun & Gallaire (Reference Viola, Brun and Gallaire2018) where the stick–slip CL dynamics of inviscid sloshing waves subjected contact angle hysteresis is solved through of a weakly nonlinear analysis. A similar contact angle model has been also used (Ludwicki et al. Reference Ludwicki, Kern, McCraney, Bostwick, Daniel and Steen2022) to investigate numerically the coalescence of sessile drops using a three-dimensional volume-of-fluid method to track the motion of the free surface. Alternatively, an immersed boundary approach can be exploited to account for viscous, convective and buoyancy effects on sessile drops, along with their collective dynamics as done by Chong et al. (Reference Chong, Li, Ng, Verzicco and Lohse2020).
The findings of Zhang et al. (Reference Zhang, Zhou and Ding2023) shed new light on the effects of gravity on sessile drop oscillations, which deserve to be further investigated experimentally. Specifically, the frequency spectrum shift produced by gravity is seen to be sensitive to the contact angle and to the azimuthal wavenumber; comprehensive experimental studies of this aspect for high-order and non-axisymmetric modes are still lacking and they would be very welcome to complete the picture.
Declaration of interests
The authors report no conflict of interest.