Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T06:18:04.512Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall effects on pressure fluctuations in turbulent channel flow

Published online by Cambridge University Press:  27 February 2013

G. A. Gerolymos ,
D. Sénéchal  and
I. Vallet
G. A. Gerolymos
Affiliation:
Institut d’Alembert, Université Pierre et Marie Curie (UPMC), 4 place Jussieu, 75005 Paris, France
D. Sénéchal
Affiliation:
Institut d’Alembert, Université Pierre et Marie Curie (UPMC), 4 place Jussieu, 75005 Paris, France
I. Vallet*
Affiliation:
Institut d’Alembert, Université Pierre et Marie Curie (UPMC), 4 place Jussieu, 75005 Paris, France
*
†Email address for correspondence: isabelle.vallet@upmc.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

The purpose of the present paper is to study the influence of wall echo on pressure fluctuations 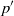${p}^{\prime } $, and on statistical correlations containing 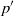${p}^{\prime } $, namely, redistribution 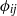${\phi }_{ij} $, pressure diffusion 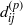${ d}_{ij}^{(p)} $ and velocity pressure-gradient 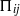${\Pi }_{ij} $. We extend the usual analysis of turbulent correlations containing pressure fluctuations in wall-bounded direct numerical simulations (Kim, J. Fluid Mech., vol. 205, 1989, pp. 421–451), separating 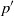${p}^{\prime } $ not only into rapid 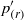${ p}_{(r)}^{\prime } $ and slow 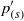${ p}_{(s)}^{\prime } $ parts (Chou, Q. Appl. Maths, vol. 3, 1945, pp. 38–54), but also further into volume (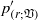${ p}_{(r; \mathfrak{V})}^{\prime } $ and 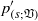${ p}_{(s; \mathfrak{V})}^{\prime } $) and surface (wall echo, 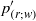${ p}_{(r; w)}^{\prime } $ and 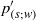${ p}_{(s; w)}^{\prime } $) terms. An algorithm, based on a Green’s function approach, is developed to compute the above splittings for various correlations containing pressure fluctuations (redistribution, pressure diffusion, velocity pressure-gradient), in fully developed turbulent plane channel flow. This exact analysis confirms previous results based on a method-of-images approximation (Manceau, Wang & Laurence, J. Fluid Mech., vol. 438, 2001, pp. 307–338) showing that, at the wall, 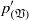${ p}_{(\mathfrak{V})}^{\prime } $ and 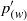${ p}_{(w)}^{\prime } $ are usually of the same sign and approximately equal. The above results are then used to study the contribution of each mechanism to the pressure correlations in low-Reynolds-number plane channel flow, and to discuss standard second-moment-closure modelling practices.

JFM classification

Turbulent Flows: Turbulence simulation Turbulent Flows: Turbulent boundary layers Turbulent Flows: Turbulent Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 720 , 10 April 2013 , pp. 15 - 65
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

del Álamo, J. C. & Jiménez, J. 2003 Spectra of the very large anisotropic scales in turbulent channels. Phys. Fluids 15 (6), L41–L44.Google Scholar
del Álamo, J. C., Jiménez, J., Zandonade, P. & Moser, R. D. 2004 Scaling of the energy spectra of turbulent channels. J. Fluid Mech. 500, 135–144.Google Scholar
Balakumar, B. J. & Adrian, R. J. 2007 Large- and very-large-scale motions in channel and boundary-layer flows. Phil. Trans. R. Soc. Lond. A 365, 665–681.Google Scholar
Bender, C. M. & Orszag, S. A. 1978 Advanced Mathematical Methods for Scientists and Engineers, pp. 16–19 Springer.Google Scholar
Bisplinghoff, R. L. & Ashley, H. 1962 Principles of Aeroelasticity, p. 76. Wiley.Google Scholar
Briggs, W. L. & Henson, V. E. 1995 The DFT: An Owner’s Manual for the Discrete Fourier Transform, pp. 144–150 SIAM.Google Scholar
Chang, P. A. III, Piomelli, U. & Blake, W. K. 1999 Relations between wall-pressure and velocity-field sources. Phys. Fluids 11 (11), 3434–3448.CrossRefGoogle Scholar
Cheng, H., Huang, J. & Leiterman, T. J. 2006 An adaptive fast solver for the modified Helmholtz equation in 2-D. J. Comput. Phys. 211, 616–637.Google Scholar
Chou, P. Y. 1945 On velocity correlations and the solutions of the equations of turbulent fluctuations. Q. Appl. Maths 3, 38–54.Google Scholar
Coleman, G. N., Kim, J. & Moser, R. D. 1995 A numerical study of turbulent supersonic isothermal-wall channel flow. J. Fluid Mech. 305, 159–183.CrossRefGoogle Scholar
Corcos, G. M. 1964 The structure of the turbulent pressure field in boundary-layer flows. J. Fluid Mech. 18, 353–378.CrossRefGoogle Scholar
Cormack, D. E. 1975 Topics in geophysical fluid dynamics: I. Natural convection in shallow cavities. II. Studies of a phenomenological turbulence model. PhD thesis, California Institute of Technology, Pasadena.Google Scholar
Courant, R. & Hilbert, D. 1953 Methods of Mathematical Physics, vol. I, pp. 351–358, 371–377. Interscience.Google Scholar
Craft, T. J. & Launder, B. 1996 A Reynolds-stress model designed for complex geometries. Intl J. Heat Fluid Flow 17, 245–254.Google Scholar
Daly, B. J. & Harlow, F. H. 1970 Transport equations in turbulence. Phys. Fluids 13, 2634–2649.Google Scholar
Davidson, P. A. 2004 Turbulence. Oxford University Press.Google Scholar
Donaldson, C. du P. 1969 A computer study of an analytical model of boundary-layer transition. AIAA J. 7 (2), 271–278.Google Scholar
Dosio, A., Vilà-Guerau de Arellano, J., Holtslag, A. A. M. & Builtjes, P. J. H. 2005 Relating Eulerian and Lagrangian statistics for the turbulent dispersion in the atmospheric convective boundary-layer. J. Atmos. Sci. 62 (4), 1175–1191.Google Scholar
Durbin, P. A. 1993 A Reynolds-stress model for near-wall turbulence. J. Fluid Mech. 249, 465–498.Google Scholar
Durbin, P. A. 1995 Separated flow computation with the $k$ – $\varepsilon $ – ${v}^{2} $ model. AIAA J. 33 (4), 659–664.Google Scholar
Durran, D. R. 1989 Improving the anelastic approximation. J. Atmos. Sci. 46 (11), 1453–1461.Google Scholar
Favre, A. 1965a Equations des gaz turbulents compressibles – I – formes générales. J. Méc. 4, 361–390.Google Scholar
Favre, A. 1965b Equations des gaz turbulents compressibles – II – méthode des vitesses moyennes; méthode des vitesses moyennes pondérées par la masse volumique. J. Méc. 4, 391–421.Google Scholar
Foysi, H., Sarkar, S. & Friedrich, R. 2004 Compressibility effects and turbulence scalings in supersonic channel flow. J. Fluid Mech. 509, 207–216.Google Scholar
Fu, S. 1993 Modelling of the pressure–velocity correlation in turbulence diffusion. Comput. Fluids 22, 199–205.Google Scholar
Garrick, I. E. 1957 Nonsteady wing charactreristics. In Aerodynamic Components of Aircraft at High Speeds (ed. Donovan, A. F. & Lawrence, H. R.), High Speed Aerodynamics and Jet Propulsion, vol. VII, pp. 658–793. Princeton University Press.Google Scholar
Gerolymos, G. A., Lo, C. & Vallet, I. 2012a Tensorial representations of Reynolds-stress pressure–strain redistribution. Trans. ASME: J. Appl. Mech. 79 (4), 044506.CrossRefGoogle Scholar
Gerolymos, G. A., Lo, C., Vallet, I. & Younis, B. A. 2012b Term-by-term analysis of near-wall second moment closures. AIAA J. 50 (12), 2848–2864.Google Scholar
Gerolymos, G. A., Sauret, E. & Vallet, I. 2004 Contribution to the single-point-closure Reynolds-stress modelling of inhomogeneous flow. Theor. Comput. Fluid Dyn. 17 (5–6), 407–431.Google Scholar
Gerolymos, G. A., Sénéchal, D. & Vallet, I. 2009 Very-high-order WENO schemes. J. Comput. Phys. 228, 8481–8524.Google Scholar
Gerolymos, G. A., Sénéchal, D. & Vallet, I. 2010 Performance of very-high-order upwind schemes for DNS of compressible wall-turbulence. Intl J. Numer. Meth. Fluids 63, 769–810.CrossRefGoogle Scholar
Gerolymos, G. A. & Vallet, I. 2001 Wall-normal-free near-wall Reynolds-stress closure for 3-D compressible separated flows. AIAA J. 39 (10), 1833–1842.Google Scholar
Gerolymos, G. A. & Vallet, I. 2009 SourceForge: aerodynamics. http://sourceforge.net/projects/aerodynamics.Google Scholar
Gibson, M. M. & Launder, B. E. 1978 Ground effects on pressure fluctuations in the atmospheric boundary-layer. J. Fluid Mech. 86, 491–511.Google Scholar
Goody, M. 2004 Empirical spectral model of surface pressure fluctuations. AIAA J. 42 (9), 1788–1794.Google Scholar
Hamba, F. 1999 Effects of pressure fluctuations on turbulence growth in compressible homogeneous shear flow. Phys. Fluids 11 (6), 1623–1635.Google Scholar
Hanjalić, K. 1994 Advanced turbulence closure models: a view of current status and future prospects. Intl J. Heat Fluid Flow 15, 178–203.Google Scholar
Harris, J. W. & Stocker, H. 1998 Handbook of Mathematics and Computational Science. Springer.Google Scholar
Hirt, C. W. 1969 Generalized turbulence transport equations. International Semuinar of the International Center for Heat and Mass Transfer, Herceg Novi, Yugoslavia.Google Scholar
Hoyas, S. & Jiménez, J. 2006 Scaling of the velocity fluctuations in turbulent channels up to $R{e}_{\tau } = 2003$ . Phys. Fluids 18, 011702.Google Scholar
Hoyas, S. & Jiménez, J. 2008 Reynolds number effects on the Reynolds-stress budgets in turbulent channels. Phys. Fluids 20, 101511.Google Scholar
Hu, Z. W., Morfey, C. L. & Sandham, N. D. 2002 Aeroacoustics of wall-bounded turbulent flow. AIAA J. 40 (3), 465–473.Google Scholar
Hu, Z. W., Morfey, C. L. & Sandham, N. D. 2006 Wall pressure and shear stress spectra from direct simulations of channel flow. AIAA J. 44 (7), 1541–1549.Google Scholar
Hu, Z. W. & Sandham, N. D. 2001 DNS databases for turbulent Couette and Poiseuille flow. Tech. Rep. AFM-01-04. AFM Research Group, School of Engineering Sciences, University of Southampton.Google Scholar
Huang, P. G., Coleman, G. N. & Bradshaw, P. 1995 Compressible turbulent channel flows: DNS results and modelling. J. Fluid Mech. 305, 185–218.Google Scholar
Hunt, J. C. R. & Graham, J. M. R. 1978 Free-stream turbulence near plane boundaries. J. Fluid Mech. 84, 209–235.Google Scholar
Hutchins, N. & Marusic, I. 2007 Evidence of very long meandering features in the logarithmic region of turbulent boundary-layers. J. Fluid Mech. 579, 1–28.Google Scholar
Ince, I. L. 1926 Ordinary Differential Equations, 1st edn, pp. 123–126, 254–263, 266–269. Dover.Google Scholar
Jakirlić, S. & Hanjalić, K. 2002 A new approach to modelling near-wall turbulence energy and stress dissipation. J. Fluid Mech. 459, 139–166.Google Scholar
Jovanović, J. 2004 The Statistical Dynamics of Turbulence. Springer.CrossRefGoogle Scholar
Katz, J. & Plotkin, A. 1991 Low-Speed Aerodynamics: From Wing Theory to Panel Methods, pp. 52–57 McGraw-Hill.Google Scholar
Kim, J. 1989 On the structure of pressure fluctuations in simulated turbulent channel-flow. J. Fluid Mech. 205, 421–451.Google Scholar
Kim, J., Moin, P. & Moser, R. 1987 Turbulence statistics in fully developed channel flow at low-Reynolds-number. J. Fluid Mech. 177, 133–166.Google Scholar
Launder, B. E. & Li, S. P. 1994 On the elimination of wall-topography parameters from 2-moment closure. Phys. Fluids 6, 999–1006.Google Scholar
Launder, B. E., Reece, G. J. & Rodi, W. 1975 Progress in the development of a Reynolds-stress turbulence closure. J. Fluid Mech. 68, 537–566.Google Scholar
Lumley, J. L. 1978 Computational modelling of turbulent flows. Adv. Appl. Mech. 18, 123–176.Google Scholar
Mahle, I., Foysi, H., Sarkar, S. & Friedrich, R. 2007 On the turbulence structure of inert and reacting compressible mixing layers. J. Fluid Mech. 593, 171–180.Google Scholar
Manceau, R. & Hanjalić, K. 2002 Elliptic blending model: a new near-wall Reynolds-stress turbulence closure. Phys. Fluids 14 (2), 744–754.Google Scholar
Manceau, R., Wang, M. & Laurence, D. 2001 Inhomogeneity and anisotropy effects on the redistribution term in Reynolds-averaged Navier–Stokes modelling. J. Fluid Mech. 438, 307–338.Google Scholar
Mansour, N. N., Kim, J. & Moin, P. 1988 Reynolds-stress and dissipation-rate budgets in a turbulent channel flow. J. Fluid Mech. 194, 15–44.Google Scholar
Marmanis, H. 1998 Analogy between the Navier–Stokes equations and Maxwell’s equations: application to turbulence. Phys. Fluids 10 (6), 1428–1437.Google Scholar
Miles, J. W. 1959 The Potential Theory of Unsteady Supersonic Flow, p. 2ff. Cambridge University Press.Google Scholar
Monin, A. S. & Yaglom, A. M. 1971 Statistical Fluid Mechanics: Mechanics of Turbulence, vol. 1. MIT Press.Google Scholar
Moser, R. D., Kim, J. & Mansour, N. N. 1999 Direct numerical simulation of turbulent channel flow up to $R{e}_{\tau } = 590$ . Phys. Fluids 11 (4), 943–945.Google Scholar
Myint-U, T. & Debnath, L. 2007 Linear Partial Differential Equations for Scientists and Engineers, 4th edn, pp. 310–317 Birkhäuser.Google Scholar
Naka, Y., Omori, T., Obi, S. & Masuda, S. 2006 Simultaneous measurements of fluctuating velocity and pressure in a turbulent mixing layer. Intl J. Heat Fluid Flow 27, 737–746.Google Scholar
Ockendon, J., Howison, S., Lacey, A. & Movchan, A. 2003 Applied Partial Differential Equations, rev. edn, pp. 163–166, 169–174. Oxford University Press.Google Scholar
Pantano, C. & Sarkar, S. 2002 A study of compressibility effects in the high-speed turbulent shear layer using direct simulation. J. Fluid Mech. 451, 329–371.Google Scholar
Panton, R. L. & Linebarger, J. H. 1974 Wall pressure spectra calculations for equilibrium boundary-layers. J. Fluid Mech. 65, 261–287.Google Scholar
Perot, B. 1999 Turbulence modelling using body-force potentials. Phys. Fluids 11 (9), 2645–2656.Google Scholar
Piquet, J. 1999 Turbulent Flows – Models and Physics. Springer.Google Scholar
Pope, S. B. 2000 Turbulent Flows. Cambridge University Press.Google Scholar
Ristorcelli, J. R. 1997 A pseudosound constitutive relationship for the dilatational covariances in compressible turbulence. J. Fluid Mech. 347, 37–70.Google Scholar
Ristorcelli, J. R., Lumley, J. L. & Abid, R. 1995 A rapid-pressure covariance representation consistent with the Taylor–Proudman theorem materially frame indifferent in the 2-D limit. J. Fluid Mech. 292, 111–152.Google Scholar
Rotta, J. 1951a Statistische Theorie nichthomogener Turbulenz – 1. Mitteilung. Z. Phys. 129, 547–572.Google Scholar
Rotta, J. 1951b Statistische Theorie nichthomogener Turbulenz – 2. Mitteilung. Z. Phys. 131, 51–77.Google Scholar
Sauret, E. & Vallet, I. 2007 Near-wall turbulent pressure diffusion modelling and influence in 3-D secondary flows. Trans. ASME: J. Fluids Engng 129 (5), 634–642.Google Scholar
Schwarz, W. R. & Bradshaw, P. 1994 Term-by-term tests of stress-transport turbulence models in a 3-D boundary-layer. Phys. Fluids A 6 (2), 986–998.CrossRefGoogle Scholar
Shih, T. H. & Lumley, J. L. 1993 Critical comparison of 2-order closures with direct numerical simulations of homogeneous turbulence. AIAA J. 31 (4), 663–670.Google Scholar
Shir, C. C. 1973 A preliminary numerical study of atmospheric turbulent flows in the idealized planetary boundary-layer. J. Atmos. Sci. 30, 1327–1339.Google Scholar
So, R. M. C., Gatski, T. B. & Sommer, T. P. 1998 Morkovin hypothesis and the modelling of wall-bounded compressible turbulent flows. AIAA J. 36 (9), 1583–1592.Google Scholar
Speziale, C. G., Sarkar, S. & Gatski, T. B. 1991 Modelling the pressure–strain correlation of turbulence: an invariant dynamical systems approach. J. Fluid Mech. 227, 245–272.Google Scholar
Suga, K. 2004 Modelling the rapid part of the pressure–diffusion process in the Reynolds stress transport equation. Trans. ASME: J. Fluids Engng 126, 634–641.Google Scholar
Taulbee, D. & VanOsdol, J. 1991 Modelling turbulent compressible flows: the mass fluctuating velocity and squared density. AIAA Paper 1991-0524.Google Scholar
Tsuji, Y., Fransson, J. H. M., Alfredsson, P. H. & Johansson, A. V. 2007 Pressure statistics and their scalings in high-Reynolds-number turbulent boundary-layers. J. Fluid Mech. 585, 1–40.Google Scholar
Tsuji, Y. & Ishihara, T. 2003 Similarity scaling of pressure fluctuation in turbulence. Phys. Rev. E 68, 026309.Google Scholar
Vallet, I. 2007 Reynolds-stress modelling of 3-D secondary flows with emphasis on turbulent diffusion closure. Trans. ASME: J. Appl. Mech. 74 (6), 1142–1156.Google Scholar
Zauderer, E. 2006 Partial Differential Equations of Applied Mathematics, pp. 446–447, 451–454. Wiley.Google Scholar