Hostname: page-component-78c5997874-m6dg7 Total loading time: 0 Render date: 2024-11-10T21:19:20.920Z Has data issue: false hasContentIssue false
  • English
  • Français

Wall shear stress in accelerating turbulent pipe flow

Published online by Cambridge University Press:  21 September 2011

S. He ,
C. Ariyaratne  and
A. E. Vardy
S. He*
Affiliation:
Department of Mechanical Engineering, University of Sheffield, Sheffield S1 3JD, UK
C. Ariyaratne
Affiliation:
Thermo-Fluid Mechanics Research Centre, University of Sussex, Brighton BN1 9QT, UK
A. E. Vardy
Affiliation:
Division of Civil Engineering, University of Dundee, Dundee DD1 4HN, Scotland, UK
*
†Email address for correspondence: s.he@sheffield.ac.uk
Get access Rights & Permissions [Opens in a new window]

Abstract

An experimental study of wall shear stress in an accelerating flow of water in a pipe ramping between two steady turbulent flows has been undertaken in a large-scale experimental facility. Ensemble averaged mean and r.m.s. of the turbulent fluctuations of wall shear stresses have been derived from hot-film measurements from many repeated runs. The initial Reynolds number and the acceleration rate were varied systematically to give values of a non-dimensional acceleration parameter 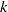ranging from 0.16 to 14. The wall shear stress has been shown to follow a three-stage development. Stage 1 is associated with a period of minimal turbulence response; the measured turbulent wall shear stress remains largely unchanged except for a very slow increase which is readily associated with the stretching of existing turbulent eddies as a result of flow acceleration. In this condition of nearly ‘frozen’ turbulence, the unsteady wall shear stress is driven primarily by flow inertia, initially increasing rapidly and overshooting the pseudo-steady value, but then increasing more slowly and eventually falling below the pseudo-steady value. This variation is predicted by an analytical expression derived from a laminar flow formulation. The start of Stage 2 is marked by the generation of new turbulence causing both the mean and turbulent wall shear stress to increase rapidly, although there is a clear offset between the responses of these two quantities. The turbulent wall shear, reflecting local turbulent activities near the wall, responds first and the mean wall shear, reflecting conditions across the entire flow field, responds somewhat later. In Stage 3, the wall shear stress exhibits a quasi-steady variation. The duration of the initial period of nearly frozen turbulence response close to the wall increases with decreasing initial Reynolds number and with increasing acceleration. The latter is in contrast to the response of turbulence in the core of the flow, which previous measurements have shown to be independent of the rate of acceleration.

JFM classification

Turbulent Flows: Pipe flow
Type
Papers
Information
Journal of Fluid Mechanics , Volume 685 , 25 October 2011 , pp. 440 - 460
Copyright
Copyright © Cambridge University Press 2011

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Ainola, L., Koppel, T., Lamp, J. & Liiv, U. 1983 The skin friction coefficient during accelerated flows in pipes. In Proceedings XX IAHR Congress, Moscow, USSR, vol. 6, pp. 453–460.Google Scholar
2. Ariyaratne, C., Wang, F., He, S. & Vardy, A. E. 2010. Use of hot-film anemometry for wall shear stress measurements in unsteady flows. In International Heat Transfer Conference. August 8–13, Washington DC, USA, IHTC14-22674.Google Scholar
3. Brereton, G. J. & Reynolds, W. C. 1991 Dynamic response of boundary-layer turbulence to oscillatory shear. Phys. Fluids A 3, 178–187.CrossRefGoogle Scholar
4. Brereton, G. J., Reynolds, W. C. & Jayaraman, R. 1990 Response of a turbulent boundary layer to sinusoidal free stream unsteadiness. J. Fluid Mech. 221, 131–159.CrossRefGoogle Scholar
5. Brunone, B., Karney, B. W., Micarelli, M. & Ferrante, M. 2000 Velocity profiles and unsteady pipe friction in transient flow. J. Water Resour. Plng Mgmt ASCE 126 (4), 236–244.CrossRefGoogle Scholar
6. Chew, Y. T., Khoo, B. C., Lim, C. P. & Teo, C. J. 1998 Dynamic response of a hot-wire anemometre. Part II: A flush-mounted hot-wire and hot-film probes for wall shear stress measurements. Meas. Sci. Technol. 9, 764–778.CrossRefGoogle Scholar
7. Chung, Y. M. 2005 Unsteady turbulent flow with sudden pressure gradient changes. Intl J. Numer. Meth. Fluids 47, 925–930.CrossRefGoogle Scholar
8. Das, D. & Arakeri, J. H. 1998 Transition of unsteady velocity profiles with reverse flow. J. Fluid Mech. 374, 251–283.CrossRefGoogle Scholar
9. Gerrard, J. H. 1971 An experimental investigation of pulsating turbulent water flow in a tube. J. Fluid Mech. 46, 43–64.CrossRefGoogle Scholar
10. Ghidaoui, M. S. & Kolyshkin, A. A. 2001 Stability analysis of velocity profiles in water–hammer flows. J. Hydraul. Engng ASCE 127 (6), 499–512.CrossRefGoogle Scholar
11. Greenblatt, D. & Moss, E. A. 1999 Pipe-flow relaminarization by temporal acceleration. Phys. Fluids 11, 3478–3481.CrossRefGoogle Scholar
12. Greenblatt, D. & Moss, E. A. 2004 Rapid temporal acceleration of a turbulent pipe flow. J. Fluid Mech. 514, 65–75.CrossRefGoogle Scholar
13. He, S. & Ariyaratne, C. 2011 Wall shear stress in the early stage of unsteady turbulent pipe flow. J. Hydraul. Engng 137, 606–610.CrossRefGoogle Scholar
14. He, S., Ariyaratne, C. & Vardy, A. E. 2008 A computational study of wall friction and turbulence dynamics in accelerating pipe flows. Comput. Fluids 37, 674–689.CrossRefGoogle Scholar
15. He, S. & Jackson, J. D. 2000 A study of turbulence under conditions of transient flow in a pipe. J. Fluid Mech. 408, 1–38.CrossRefGoogle Scholar
16. He, S. & Jackson, J. D. 2001 Wall shear stress in accelerating pipe flows. In Energy Conversion and Application (Proceedings International Conference on Energy Conversion & Application, Wuhan, China). pp. 442–448.Google Scholar
17. He, S. & Jackson, J. D. 2009 An experimental study of pulsating turbulent flow in a pipe. Eur. J. Mech. (B/Fluids) 28, 309–320.CrossRefGoogle Scholar
18. Kasar, S., Shah, R. K. & Aung, W. 1987 Handbook of Single-Phase Convective Heat Transfer. John Wiley & Sons.Google Scholar
19. Knisely, C. W., Nishihara, K & Iguchi, M. 2010 Critical Reynolds number in constant-acceleration pipe flow from an initial steady laminar state. J. Fluids Engng 123, 091202.CrossRefGoogle Scholar
20. Mao, Z. & Hanratty, T. J. 1986 Studies of wall shear stress in a turbulent pulsating pipe flow. J. Fluid Mech. 170, 545–564.CrossRefGoogle Scholar
21. Mao, Z. & Hanratty, T. J. 1992 Measurement of wall shear rate in large amplitude unsteady reversing flows. Exp. Fluids 12, 342.CrossRefGoogle Scholar
22. Maruyama, T., Kuribayashi, T. & Mizushima, T. 1976 The structure of turbulence in transient pipe flows. J. Chem. Engng Japan 9, 431–439.CrossRefGoogle Scholar
23. Piomelli, U., Balaras, E. & Pascarelli, A. 2000 Turbulent structures in accelerating boundary layers. J. Turbul. 1, 1–16.CrossRefGoogle Scholar
24. Proudovsky, A. M. 1997 Wall shear stress in accelerating and decelerating pipe flows. J. Hydraul. Res. 35 (1), 133–136.CrossRefGoogle Scholar
25. Proudovsky, A. M. & Oreshkin, O. F. 1985 The characteristics of unsteady fluid flows. In Proceedings of XXI IAHR Congress Seminar 3, Melbourne.Google Scholar
26. Ramaprian, B. R. & Tu, S. W. 1983 Fully developed periodic turbulent pipe flow. Part 2. The detailed structure of the flow. J. Fluid Mech. 137, 59–81.CrossRefGoogle Scholar
27. Ronneberger, D. & Aherens, C. D. 1977 Wall shear stress caused by small amplitude perturbations of turbulent boundary-layer flows: an experimental investigation. J. Fluid Mech. 83, 433–464.CrossRefGoogle Scholar
28. Ruedi, J. D., Nagib, H., Osterlund, J. & Monkewitz, P. A. 2004 Unsteady wall-shear measurements in turbulent boundary layers using MEMS. Exp. Fluids 36, 393–398.Google Scholar
29. Scotti, A. & Piomelli, U. 2001 Numerical simulation of pulsating turbulent channel flow. Phys. Fluids 13, 1367–1384.CrossRefGoogle Scholar
30. Shemer, L., Wygnanski, I. & Kit, E. 1985 Pulsating flow in a pipe. J. Fluid Mech. 153, 313–337.CrossRefGoogle Scholar
31. Shuy, E. B. 1996 Wall shear stress in accelerating and decelerating turbulent pipe flows. J. Hydraul. Res. 34, 173–183.CrossRefGoogle Scholar
32. Tardu, S. F. & Binder, G. 1993 Wall shear stress modulation in unsteady turbulent channel flow with high imposed frequencies. Phys. Fluids A 5, 2028–2037.CrossRefGoogle Scholar
33. Tardu, S. F., Binder, G. & Blackwelder, R. F. 1994 Turbulent channel flow with large-amplitude velocity oscillations. J. Fluid Mech. 267, 109–151.CrossRefGoogle Scholar
34. Tardu, S. F. & Da Costa, P. 2005 Experiments and modelling of an unsteady turbulent channel flow. AIAA J. 43, 140–148.CrossRefGoogle Scholar
35. Tardu, S. F. & Pham, C. T. 2005 Response of wall hot-film gages with longitudinal diffusion and heat conduction to the substrate. Trans. ASME: J. Heat Transfer 127, 812–819.CrossRefGoogle Scholar
36. Tu, S. W. & Ramaprian, B. R. 1983 Fully developed periodic turbulent pipe flow. Part 1. Main experimental results and comparison with predictions. J. Fluid Mech. 137, 31–58.CrossRefGoogle Scholar
37. Vardy, A. E. & Brown, J. M. B. 2003 Transient turbulent friction in smooth pipe flows. J. Sound Vib. 259, 1011–1036.CrossRefGoogle Scholar
38. Zhao, M., Ghidaoui, M. S. & Kolyshkin, A. A. 2007 Perturbation dynamics in unsteady pipe flows. J. Fluid Mech. 570, 129–154.CrossRefGoogle Scholar