Hostname: page-component-78c5997874-lj6df Total loading time: 0 Render date: 2024-11-10T15:10:08.343Z Has data issue: false hasContentIssue false
  • English
  • Français

Water entry of spheres with various contact angles

Published online by Cambridge University Press:  10 January 2019

Nathan B. Speirs ,
Mohammad M. Mansoor Open the ORCID record for Mohammad M. Mansoor [Opens in a new window] ,
Jesse Belden Open the ORCID record for Jesse Belden [Opens in a new window]  and
Tadd T. Truscott Open the ORCID record for Tadd T. Truscott [Opens in a new window]
Nathan B. Speirs
Affiliation:
Department of Mechanical and Aerospace Engineering, Utah State University, Logan, UT 84322, USA
Mohammad M. Mansoor
Affiliation:
Department of Mechanical and Aerospace Engineering, Utah State University, Logan, UT 84322, USA
Jesse Belden
Affiliation:
Naval Undersea Warfare Center, 1176 Howell Street, Newport, RI 02841, USA
Tadd T. Truscott*
Affiliation:
Department of Mechanical and Aerospace Engineering, Utah State University, Logan, UT 84322, USA
*
†Email address for correspondence: taddtruscott@gmail.com
Get access Rights & Permissions [Opens in a new window]

Abstract

It is well known that the water entry of a sphere causes cavity formation above a critical impact velocity as a function of the solid–liquid contact angle; Duez et al. (Nat. Phys., vol. 3 (3), 2007, pp. 180–183). Using a rough sphere with a contact angle of 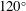$120^{\circ }$, Aristoff & Bush (J. Fluid Mech., vol. 619, 2009, pp. 45–78) showed that there are four different cavity shapes dependent on the Bond and Weber numbers (i.e., quasistatic, shallow, deep and surface). We experimentally alter the Bond number, Weber number and contact angle of smooth spheres and find two key additions to the literature: (1) cavity shape also depends on the contact angle; (2) the absence of a splash crown at low Weber number results in cavity formation below the predicted critical velocity. In addition, we use alternate scales in defining the Bond, Weber and Froude numbers to predict the cavity shapes and scale pinch-off times for various impacting bodies (e.g., spheres, multidroplet streams and jets) on the same plots, merging the often separated studies of solid–liquid and liquid–liquid impact in the literature.

JFM classification

Interfacial Flows (free surface): Interfacial Flows (free surface)
Type
JFM Rapids
Information
Journal of Fluid Mechanics , Volume 862 , 10 March 2019 , R3
Copyright
© 2019 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Aristoff, J. M. & Bush, J. W. M. 2009 Water entry of small hydrophobic spheres. J. Fluid Mech. 619, 45–78.Google Scholar
Aristoff, J. M., Truscott, T. T., Techet, A. H. & Bush, J. W. M. 2010 The water entry of decelerating spheres. Phys. Fluids 22 (3), 032102.Google Scholar
Birkhoff, G. & Isaacs, R.1951 Transient cavities in air-water entry. Navord Report 1490. Tech. Rep.Google Scholar
Bouwhuis, W., Huang, X., Chan, C. U., Frommhold, P. E., Ohl, C.-D., Lohse, D., Snoeijer, J. H. & van der Meer, D. 2016 Impact of a high-speed train of microdrops on a liquid pool. J. Fluid Mech. 792, 850–868.Google Scholar
Duclaux, V., Caillé, F., Duez, C., Ybert, C., Bocquet, L. & Clanet, C. 2007 Dynamics of transient cavities. J. Fluid Mech. 591, 1–19.Google Scholar
Duez, C., Ybert, C., Clanet, C. & Bocquet, L. 2007 Making a splash with water repellency. Nat. Phys. 3 (3), 180–183.Google Scholar
Gilbarg, D. & Anderson, R. A. 1948 Influence of atmospheric pressure on the phenomena accompnaying the entry of spheres into water. J. Appl. Phys. 19, 127–139.Google Scholar
Hurd, R. C., Belden, J., Jandron, M. A., Fanning, D. T., Bower, A. F. & Truscott, T. T. 2017 Water entry of deformable spheres. J. Fluid Mech. 824, 912–930.Google Scholar
Lohse, D., Bergmann, R., Mikkelsen, R., Zeilstra, C., van der Meer, D., Versluis, M., van der Weele, K., van der Hoef, M. & Kuipers, H. 2004 Impact on soft sand: void collapse and jet formation. Phys. Rev. Lett. 93, 198003.Google Scholar
Mansoor, M. M., Marston, J. O., Vakarelski, I. U. & Thoroddsen, S. T. 2014 Water entry without surface seal: extended cavity formation. J. Fluid Mech. 743, 295–326.Google Scholar
Marston, J. O. & Thoroddsen, S. T. 2008 Apex jets from impacting drops. J. Fluid Mech. 614, 293–302.Google Scholar
Marston, J. O., Truscott, T. T., Speirs, N. B., Mansoor, M. M. & Thoroddsen, S. T. 2016 Crown sealing and buckling instability during water entry of spheres. J. Fluid Mech. 794, 506–529.Google Scholar
May, A. 1951 Effect of surface condition of a sphere on its water-entry cavity. J. Appl. Phys. 22 (10), 1219–1222.Google Scholar
Oguz, H. N., Prosperetti, A. & Kolaini, A. R. 1995 Air entrapment by a falling water mass. J. Fluid Mech. 294, 181–207.Google Scholar
Oguz, H. N., Prosperetti, A. & Lezzi, A. M. 1992 Examples of air-entraining flows. Phys. Fluids A 4 (4), 649–651.Google Scholar
Qu, X., Goharzadeh, A., Khezzar, L. & Molki, A. 2013 Experimental characterization of air-entrainment in a plunging jet. Exp. Therm. Fluid Sci. 44, 51–61.Google Scholar
Speirs, N. B., Pan, Z., Belden, J. & Truscott, T. T. 2018 The water entry of multi-droplet streams and jets. J. Fluid Mech. 844, 1084–1111.Google Scholar
Truscott, T. T., Epps, B. P. & Belden, J. 2014 Water entry of projectiles. Annu. Rev. Fluid Mech. 46 (1), 355–378.Google Scholar
Truscott, T. T., Epps, B. P. & Techet, A. H. 2012 Unsteady forces on spheres during free-surface water entry. J. Fluid Mech. 704, 173–210.Google Scholar
Truscott, T. T. & Techet, A. H. 2009a A spin on cavity formation during water entry of hydrophobic and hydrophilic spheres. Phys. Fluids 21 (12), 121703.Google Scholar
Truscott, T. T. & Techet, A. H. 2009b Water entry of spinning spheres. J. Fluid Mech. 625, 135–165.Google Scholar
Zhao, M.-H., Chen, X.-P. & Wang, Q. 2014 Wetting failure of hydrophilic surfaces promoted by surface roughness. Sci. Rep. 4, 5376.Google Scholar
Zhu, Y., Oguz, H. N. & Prosperetti, A. 2000 On the mechanism of air entrainment by liquid jets at a free surface. J. Fluid Mech. 404, 151–177.Google Scholar

Speirs et al. supplementary movie 1

A 3 mm diameter sphere impacts a quiescent pool surface with velocity Uo=4.43 m/s and static contact angle θ=101.0˚ without forming a cavity. The movie is played back at 0.6% of real speed.

Download Speirs et al. supplementary movie 1(Video)
Video 616.4 KB

Speirs et al. supplementary movie 2

A 3 mm diameter sphere impacts a quiescent pool surface with velocity Uo=0.24 m/s and static contact angle θ=141.1˚ forming a quasi-static seal cavity. The movie is played back at 0.6% of real speed.

Download Speirs et al. supplementary movie 2(Video)
Video 1.9 MB

Speirs et al. supplementary movie 3

A 3 mm diameter sphere impacts a quiescent pool surface with velocity Uo=1.40 m/s and static contact angle θ=141.1˚ forming a shallow seal cavity. Deep seal quickly follows shallow seal in this case. The movie is played back at 0.6% of real speed.

Download Speirs et al. supplementary movie 3(Video)
Video 3.1 MB

Speirs et al. supplementary movie 4

A 3 mm diameter sphere impacts a quiescent pool surface with velocity Uo=2.80 m/s and static contact angle θ=141.1˚ forming a deep seal cavity. The movie is played back at 0.6% of real speed.

Download Speirs et al. supplementary movie 4(Video)
Video 1.4 MB

Speirs et al. supplementary movie 5

A 3 mm diameter sphere impacts a quiescent pool surface with velocity Uo=4.43 m/s and static contact angle θ=141.1˚ forming a surface seal cavity. The movie is played back at 0.6% of real speed.

Download Speirs et al. supplementary movie 5(Video)
Video 2.2 MB

Speirs et al. supplementary movie 6

A 10 mm diameter sphere impacts a quiescent pool surface with velocity Uo=6.26 m/s and static contact angle θ=101.1˚ forming a partial surface seal cavity. The movie is played back at 0.6% of real speed.

Download Speirs et al. supplementary movie 6(Video)
Video 1.7 MB