1. Introduction
Metamaterials, which are artificial composite structures engineered to have a property that is not found in naturally occurring materials, have emerged as a new frontier of science involving material science, physics, engineering, chemistry and biology (Liu & Zhang Reference Liu and Zhang2011; Higgins et al. Reference Higgins, Becce, Belessiotis-Richards, Seong, Sero and Stevens2020). The design of metamaterials has generated a completely new field of study on waves at different length scales ranging from, for example, microwaves of small scale (Chen et al. Reference Chen, Hou, Chen, Ao, Wen and Chan2009; Sadeghi et al. Reference Sadeghi, Li, Xu, Hou and Chen2015) to ground-borne vibrations of large scale (Palermo et al. Reference Palermo, Krödel, Marzani and Daraio2016). In recent decades, water wave interaction with metamaterial structures has been paid increasing attention by scholars.
In the field of water wave interactions with metamaterials, Berraquero et al. (Reference Berraquero, Maurel, Petitjeans and Pagneux2013) carried out a series of quantitative experimental tests of water wave control using a metamaterial, which was realised with a layered structure with alternating layers. They demonstrated that metamaterials with anisotropic properties could be employed in the context of water waves to produce a reflectionless bent waveguide. Maurel et al. (Reference Maurel, Marigo, Cobelli, Petitjeans and Pagneux2017) reported that significant anisotropic parameters could be produced by metamaterials made from a subwavelength layered structuration of the bathymetry in the shallow water regime. Porter (Reference Porter2018) proposed a theoretical model to study wave interaction with a metamaterial device formed from closely spaced arrays of thin parallel plates that extend throughout the fluid depth and occupy an infinitely long rectangular domain. He found that plane waves incident from special directions were unaffected by the device, resulting in interesting negative refractive and Goos–Hänchen shift effects, which were later reported fully in Porter (Reference Porter2021). Marangos & Porter (Reference Marangos and Porter2021) developed a shallow water theory to study wave scattering over structured bathymetry, which is composed of abrupt fluctuations in depth between two smoothly varying levels. Later, Porter & Marangos (Reference Porter and Marangos2022) proposed a full depth-dependent solution to scattering of oblique waves by a long submerged uniform rectangular ridge formed by a plate array, demonstrating that perfect negatively refracted transmission could be achieved for all wave frequencies for specific metamaterial ridges and wave headings.
Whilst most of the above-mentioned work concentrated on refraction across planar interfaces, Zheng, Porter & Greaves (Reference Zheng, Porter and Greaves2020b) considered water wave interaction with an array of metamaterial cylinders, each of which is formed by a closely spaced array of thin vertical plates. Their theoretical results showed that wave focusing/blocking could be achieved by the appropriate choice of plate alignment of a pair of metamaterial cylinders. Furthermore, a damping mechanism was introduced at the surface of the fluid occupied by the metamaterial cylinders in their model to consider the wave power dissipation in narrow gaps between the thin plates. Their work was later extended by Huang & Porter (Reference Huang and Porter2022) to study wave power absorption of a metamaterial cylinder-based wave energy converter, in which a pair of opposing paddles hinged below the surface were applied along the centre plane of the narrow channels. The paddles are attached to springs and dampers through which wave power is captured. Recently, Porter, Zheng & Liang (Reference Porter, Zheng and Liang2022) considered the scattering of waves by a truncated metamaterial cylinder, which consists of an array of closely spaced thin vertical plates and is fully submerged in the water with its bottom sitting on the seabed.
Apart from the metamaterials made from vertical plates closely deployed in parallel, an annular region containing an array of thin radial plates may also work as a metamaterial structure. Maling & Craster (Reference Maling and Craster2016) considered closely spaced radially arranged plates occupying an annular domain. The ability of the device to support localised wave motions was examined. Li et al. (Reference Li, Xu, Zhu, Zou, Liu, Wang and Chen2018) applied an annular metamaterial cylinder as a device for manipulating water waves. Besides the radially aligned plates, a linear variation of the depth of the fluid within the annular region was also imposed with the particular purpose of concentrating wave energy inside the cylinder. Recently, Zheng et al. (Reference Zheng, Porter, Liang and Greaves2022b) carried out analytical and numerical studies on wave scattering by an annular metamaterial cylinder consisting of a series of radially aligned closely spaced plates, and reported that there could be hardly any back scattering for a wide range of wave frequencies.
In addition to an array of closely spaced plates, the interaction of water waves with metamaterials made from other shaped components was also investigated, e.g. one-dimensional groove array (Han, Chen & Chen Reference Han, Chen and Chen2022), rigid sectors-made cloak (Farhat et al. Reference Farhat, Enoch, Guenneau and Movchan2008) and stationary surface disk arrays (Zhao, Hu & Zi Reference Zhao, Hu and Zi2021).
Most of the previous work has been focused on the wave scattering problem of metamaterial structures, i.e. assuming the structures are fixed. To the best of the authors’ knowledge, the water wave radiation problem of a metamaterial cylinder has never been studied before. The study of wave radiation by a metamaterial sheds light on the utilisation of floating metamaterial structures, e.g. wave power dissipation, wave energy harnessing, etc. In the present paper, we consider both radiation and scattering problems of waves by a surface-piercing vertical truncated metamaterial cylinder. The primary objective is to establish the fundamental knowledge regarding radiation and scattering of water waves by a truncated metamaterial cylinder, which is instrumental to the development of wave energy converters (WECs), floating breakwater, wave absorbers, etc, employing metamaterials. Unlike the geometries standing throughout the water depth considered in Porter (Reference Porter2018), Zheng et al. (Reference Zheng, Porter and Greaves2020b) and Huang & Porter (Reference Huang and Porter2022), the truncated feature makes the present model more practical when applied in deep water, and meanwhile, it brings considerable mathematical challenges to deal with, for example, within the cylindrical region defined by the cylinder radius, the field equation satisfied by the velocity potential above and below the submerged level of the bottom of the cylinder switches from a reduced two-dimensional (2-D) Laplace equation to the three-dimensional (3-D) Laplace equation. Different from the fully submerged and bottom-mounted truncated metamaterial cylinder, which was recently studied by Porter et al. (Reference Porter, Zheng and Liang2022), the considered metamaterial is surface piercing, and therefore wave effects are more pronounced. In addition, to consider the wave power dissipation in narrow gaps between the thin vertical plates, a damping mechanism is introduced at the surface of the fluid occupied by the metamaterial cylinder. Moreover, the reciprocal relationship between radiation and scattering problems of the floating metamaterial cylinder is established, which deepens the understanding of physical insights into the hydrodynamic behaviours.
The paper is organised as follows. The statement of the problem is elucidated in § 2, where the governing equations and boundary conditions are formulated in § 2.1; the expressions of the velocity potential at different regions are derived in § 2.2; the solutions of the unknown coefficients are described in § 2.3. Expressions of the free surface elevation, wave excitation forces and wave radiation forces, far-field radiation coefficient, the Haskind relation (HR)-based expressions, as well as wave power dissipation, are derived in § 3. The theoretical model is validated in § 4. The validated model is applied to some case studies, the results and discussions of which are presented in § 5 before the work is summarised in § 6.
2. Problem formulation
Scattering and radiation of water waves by a surface-piercing vertical truncated metamaterial circular cylinder deployed in the water of finite depth ![]() $h$ are considered (figure 1). The structured cylinder is composed of a closely spaced periodic array of infinitely thin surface-piercing vertical barriers, between which the fluid is allowed to flow tangentially. The radius and draft of the cylinder are denoted as
$h$ are considered (figure 1). The structured cylinder is composed of a closely spaced periodic array of infinitely thin surface-piercing vertical barriers, between which the fluid is allowed to flow tangentially. The radius and draft of the cylinder are denoted as ![]() $R$ and
$R$ and ![]() $d$, respectively.
$d$, respectively.
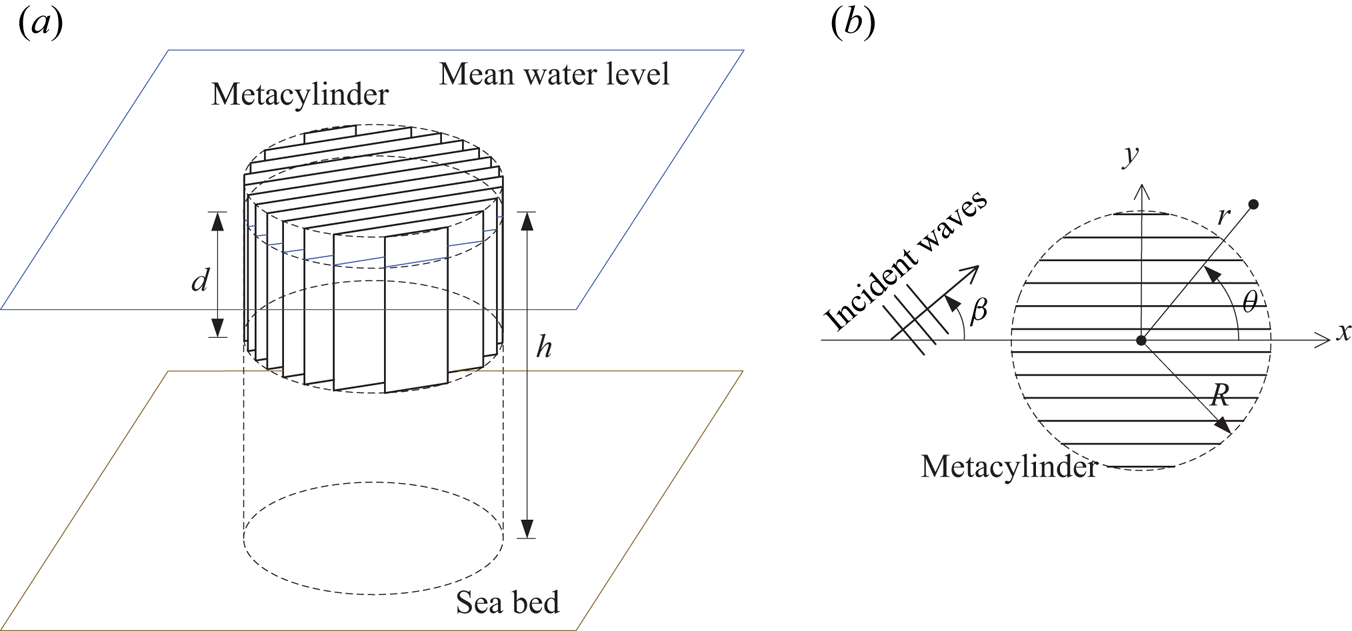
Figure 1. Illustration of the geometry: (a) bird's-eye view of the truncated metamaterial cylinder consisting of an array of closely spaced barriers; (b) a plan view showing incident wave heading with respect to the barriers.
A mixture of 3-D Cartesian and cylindrical coordinates, i.e. ![]() $Oxyz$ and
$Oxyz$ and ![]() $Or \theta z$, is chosen with
$Or \theta z$, is chosen with ![]() $z=0$ coinciding with the mean free surface of the fluid, the
$z=0$ coinciding with the mean free surface of the fluid, the ![]() $z$-axis measured vertically upwards, and the
$z$-axis measured vertically upwards, and the ![]() $x$-axis in parallel with the barriers. Hence the fluid bottom is at
$x$-axis in parallel with the barriers. Hence the fluid bottom is at ![]() $z=-h$. The cylinder is under the actions of a plane wave with angular frequency
$z=-h$. The cylinder is under the actions of a plane wave with angular frequency ![]() $\omega$, wave amplitude
$\omega$, wave amplitude ![]() $A$ and wavenumber
$A$ and wavenumber ![]() $k$ incident from infinity at an arbitrary heading angle,
$k$ incident from infinity at an arbitrary heading angle, ![]() $\beta$. The separation between plates is assumed to be small compared with both the wavelength and the length of the plate.
$\beta$. The separation between plates is assumed to be small compared with both the wavelength and the length of the plate.
2.1. Governing equations and boundary conditions
Assume that all amplitudes are small enough that classical linear water wave theory applies, and the motion is time-harmonic with an angular frequency ![]() $\omega$. Thus, the fluid velocity potential may be written as
$\omega$. Thus, the fluid velocity potential may be written as ![]() $\varPhi (x,y,z,t)={\rm Re}[\phi (x,y,z)\ \mathrm {e}^{-\mathrm {i} \omega t}]$, where
$\varPhi (x,y,z,t)={\rm Re}[\phi (x,y,z)\ \mathrm {e}^{-\mathrm {i} \omega t}]$, where ![]() ${\rm Re}$ denotes the real part,
${\rm Re}$ denotes the real part, ![]() $\phi$ represents the complex amplitude of the velocity potential at a space point
$\phi$ represents the complex amplitude of the velocity potential at a space point ![]() $(x,y,z)$ which is independent of time,
$(x,y,z)$ which is independent of time, ![]() $t$, and
$t$, and ![]() $\mathrm {i}$ is the imaginary unit. Hereinafter, the time-harmonic dependence
$\mathrm {i}$ is the imaginary unit. Hereinafter, the time-harmonic dependence ![]() $\mathrm {e}^{-\mathrm {i} \omega t}$ is suppressed, and
$\mathrm {e}^{-\mathrm {i} \omega t}$ is suppressed, and ![]() $\phi$ is adopted to represent the velocity potential. Under linear theory,
$\phi$ is adopted to represent the velocity potential. Under linear theory, ![]() $\phi$ may be decomposed as the sum of scattered and radiated wave potentials,
$\phi$ may be decomposed as the sum of scattered and radiated wave potentials,
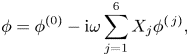 \begin{equation} \phi=\phi^{(0)} -\mathrm{i} \omega \sum_{j=1}^6 X_j \phi^{(\,j)}, \end{equation}
\begin{equation} \phi=\phi^{(0)} -\mathrm{i} \omega \sum_{j=1}^6 X_j \phi^{(\,j)}, \end{equation}
where ![]() $\phi ^{(0)}=\phi ^I+\phi ^D$ denotes the scattered wave velocity potential, in which
$\phi ^{(0)}=\phi ^I+\phi ^D$ denotes the scattered wave velocity potential, in which ![]() $\phi ^I$ and
$\phi ^I$ and ![]() $\phi ^D$ represent the undisturbed incident wave velocity potential and the diffracted velocity potential, respectively. Here
$\phi ^D$ represent the undisturbed incident wave velocity potential and the diffracted velocity potential, respectively. Here ![]() ${X}_j$ represents the complex displacement amplitude of the cylinder oscillating in the
${X}_j$ represents the complex displacement amplitude of the cylinder oscillating in the ![]() $j$th mode with
$j$th mode with ![]() $j=1,2,\ldots, 6$ denoting the surge (i.e. along the
$j=1,2,\ldots, 6$ denoting the surge (i.e. along the ![]() $x$-axis), sway (i.e. along the
$x$-axis), sway (i.e. along the ![]() $y$-axis), heave (i.e. along the
$y$-axis), heave (i.e. along the ![]() $z$-axis), roll (i.e. about the
$z$-axis), roll (i.e. about the ![]() $x$-axis), pitch (i.e. about the
$x$-axis), pitch (i.e. about the ![]() $y$-axis) and yaw (i.e. about the
$y$-axis) and yaw (i.e. about the ![]() $z$-axis), respectively, with the reference point at the origin
$z$-axis), respectively, with the reference point at the origin ![]() $(0,0,0)$. Here
$(0,0,0)$. Here ![]() $\phi ^{(\,j)}$ denotes the corresponding radiated velocity potential due to a unit amplitude velocity oscillation of the cylinder in the
$\phi ^{(\,j)}$ denotes the corresponding radiated velocity potential due to a unit amplitude velocity oscillation of the cylinder in the ![]() $j$th mode in still water. In the present paper, the plates of the cylinder are deployed in parallel with the
$j$th mode in still water. In the present paper, the plates of the cylinder are deployed in parallel with the ![]() $x$-axis, hence we only handle the modes with
$x$-axis, hence we only handle the modes with ![]() $j=2$, 4 and 6 for the wave radiation problems.
$j=2$, 4 and 6 for the wave radiation problems.
The governing equations inside and outside the cylinder give the effective field equation
and
respectively, where ![]() $\nabla _{xz}^2$ represents the 2-D Laplacian in the
$\nabla _{xz}^2$ represents the 2-D Laplacian in the ![]() $x$ and
$x$ and ![]() $z$ dimensions, and
$z$ dimensions, and ![]() $\nabla ^2$ denotes the 3-D Laplacian.
$\nabla ^2$ denotes the 3-D Laplacian.
The combined linearised dynamic and kinematic boundary condition at the free surface inside and outside the cylinder, i.e.
where ![]() $\mathcal {K}=K/(1-\bar {v}\ \mathrm{i})$ and
$\mathcal {K}=K/(1-\bar {v}\ \mathrm{i})$ and ![]() $K\equiv \omega ^2/g$, with a damping parameter
$K\equiv \omega ^2/g$, with a damping parameter ![]() $\bar {v}\ge 0$ as a means of introducing a damping mechanism and considering the possibility of energy dissipation between the plates, and
$\bar {v}\ge 0$ as a means of introducing a damping mechanism and considering the possibility of energy dissipation between the plates, and
and the bottom boundary condition
should be satisfied. Because of the narrowness of the gap between adjacent plates, fluid resonance may occur due to energy trapping. In this scenario, the friction due to boundary layers attached to the plate plays a predominant role over the flow separation from edges. Thus, the damping exhibits linear behaviour at the model scale (Zhao et al. Reference Zhao, Taylor, Wolgamot and Eatock Taylor2018; Tan et al. Reference Tan, Lu, Tang, Cheng and Chen2019; Liang et al. Reference Liang, Liu, Chua, de Mello and Choo2022). The condition presented in (2.4) could be applied to different physical settings (Zheng et al. Reference Zheng, Porter and Greaves2020b), e.g. where the surface of the narrow channels within the cylinder is covered by floating buoys constrained to move in heave (Garnaud & Mei Reference Garnaud and Mei2009), the surface of the fluid within the cylinder is covered with a porous medium (Chwang & Chan Reference Chwang and Chan1998) and the case accounting for the viscous dissipation caused by the fluid interaction with the sidewalls of the narrow rectangular fluid-filled channels with a normal air–fluid free surface (Hunt Reference Hunt1952; Mei, Stiassnie & Yue Reference Mei, Stiassnie and Yue2005). A more detailed discussion regarding the boundary condition at the free surface inside the cylinder was presented in Zheng et al. (Reference Zheng, Porter and Greaves2020b).
On ![]() $z=-d$,
$z=-d$, ![]() $r\in [0,R]$, we have
$r\in [0,R]$, we have
Over the curved surface of the cylinder, ![]() $r=R$,
$r=R$, ![]() $z\in [-d,0]$, we have
$z\in [-d,0]$, we have
representing the continuity conditions of the field in terms of pressure and mass flux, respectively, across ![]() $r=R$. Here
$r=R$. Here ![]() $\delta _{l,n}$ denotes the Kronecker delta, which equals to
$\delta _{l,n}$ denotes the Kronecker delta, which equals to ![]() $1$ when
$1$ when ![]() $l=n$ and
$l=n$ and ![]() $0$ otherwise.
$0$ otherwise.
Additionally, it is required that the diffracted and radiated waves propagate outwards for ![]() $r\rightarrow \infty$, i.e. the far-field radiation condition
$r\rightarrow \infty$, i.e. the far-field radiation condition
where ![]() $\chi$ represents
$\chi$ represents ![]() $D$ and
$D$ and ![]() $(\,j)$ for
$(\,j)$ for ![]() $j=2$, 4 and 6.
$j=2$, 4 and 6.
2.2. Expressions of the velocity potential
The fluid domain can be divided into two regions, i.e. the exterior region ![]() $r\in [R,\infty )$,
$r\in [R,\infty )$, ![]() $z\in [-h,0]$ and the interior region
$z\in [-h,0]$ and the interior region ![]() $r\in [0,R)$,
$r\in [0,R)$, ![]() $z\in [-h,0]$.
$z\in [-h,0]$.
2.2.1. Exterior region
Using the separation of variables, we may express the velocity potential at the exterior region as
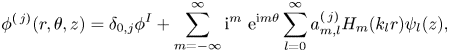 \begin{equation} \phi^{(\,j)}(r,\theta,z)= \delta_{0,j} \phi^I+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \ \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}H_m(k_l r)\psi_l(z), \end{equation}
\begin{equation} \phi^{(\,j)}(r,\theta,z)= \delta_{0,j} \phi^I+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \ \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}H_m(k_l r)\psi_l(z), \end{equation}where
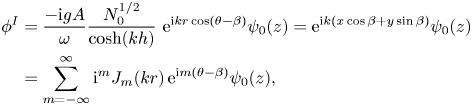 \begin{align} \phi^I&=\frac{-\mathrm{i} g A}{\omega}\frac{N_0^{{1/2}}}{\cosh(kh)}\ \mathrm{e}^{\mathrm{i} kr\cos(\theta-\beta)}\psi_0(z)=\mathrm{e}^{\mathrm{i} k(x\cos \beta + y \sin \beta)}\psi_0(z)\nonumber\\ & =\sum_{m=-\infty}^{\infty}\mathrm{i}^m J_m(k r)\, \mathrm{e}^{\mathrm{i} m (\theta-\beta)}\psi_0(z), \end{align}
\begin{align} \phi^I&=\frac{-\mathrm{i} g A}{\omega}\frac{N_0^{{1/2}}}{\cosh(kh)}\ \mathrm{e}^{\mathrm{i} kr\cos(\theta-\beta)}\psi_0(z)=\mathrm{e}^{\mathrm{i} k(x\cos \beta + y \sin \beta)}\psi_0(z)\nonumber\\ & =\sum_{m=-\infty}^{\infty}\mathrm{i}^m J_m(k r)\, \mathrm{e}^{\mathrm{i} m (\theta-\beta)}\psi_0(z), \end{align}
represents the velocity potential of the undisturbed incident waves with the complex amplitude ![]() $A={\mathrm {i} \omega \cosh (kh)}/({g N_0^{{1/2}}})$;
$A={\mathrm {i} \omega \cosh (kh)}/({g N_0^{{1/2}}})$;
in which ![]() $k_l$ are the positive real (
$k_l$ are the positive real (![]() $k_0=k$) and positive imaginary roots (for
$k_0=k$) and positive imaginary roots (for ![]() $l\ge 1$) of the dispersion relation
$l\ge 1$) of the dispersion relation ![]() $\omega ^2=g k \tanh (kh)$. Here
$\omega ^2=g k \tanh (kh)$. Here ![]() $a_{m,l}^{(\,j)}$ are unknown coefficients to be determined;
$a_{m,l}^{(\,j)}$ are unknown coefficients to be determined; ![]() $J_m$ and
$J_m$ and ![]() $H_m$ denote the Bessel functions of the first-kind and Hankel functions, respectively, of order
$H_m$ denote the Bessel functions of the first-kind and Hankel functions, respectively, of order ![]() $m$.
$m$.
The orthogonality condition
holds for ![]() $l,n=0, 1, 2, \ldots$.
$l,n=0, 1, 2, \ldots$.
2.2.2. Interior region
The solution of the velocity potential at the interior region, i.e. ![]() $r\in [0,R]$,
$r\in [0,R]$, ![]() $z\in [-d,0]$, is more complicated since there are two distinct subdomains: one within and the other below the truncated metamaterial cylinder, and the corresponding governing equations differ. The solutions at these two subdomains are connected by the conditions (2.7a,b). Following Porter et al. (Reference Porter, Zheng and Liang2022), we may write the solution in the interior region satisfying (2.2) and (2.3) in
$z\in [-d,0]$, is more complicated since there are two distinct subdomains: one within and the other below the truncated metamaterial cylinder, and the corresponding governing equations differ. The solutions at these two subdomains are connected by the conditions (2.7a,b). Following Porter et al. (Reference Porter, Zheng and Liang2022), we may write the solution in the interior region satisfying (2.2) and (2.3) in ![]() $z\in [-d,0]$ and
$z\in [-d,0]$ and ![]() $z\in [-h,-d]$, respectively, in its most general form
$z\in [-h,-d]$, respectively, in its most general form
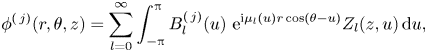 \begin{equation} \phi^{(\,j)}(r,\theta,z)=\sum_{l=0}^{\infty}\int_{-{\rm \pi}}^{\rm \pi}B_l^{(\,j)}(u)\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}Z_l(z,u)\,{\rm d}u, \end{equation}
\begin{equation} \phi^{(\,j)}(r,\theta,z)=\sum_{l=0}^{\infty}\int_{-{\rm \pi}}^{\rm \pi}B_l^{(\,j)}(u)\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}Z_l(z,u)\,{\rm d}u, \end{equation}
which is a superposition over all possible wavenumbers and wave angles, where ![]() $B_{l}^{(\,j)}(u)$ are undetermined functions,
$B_{l}^{(\,j)}(u)$ are undetermined functions,
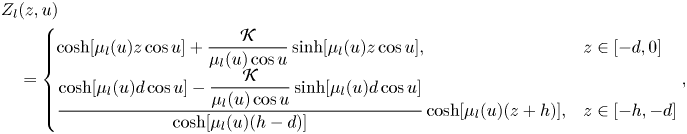 \begin{align} &Z_l(z,u)\nonumber\\ &\quad = \begin{cases} \displaystyle \cosh[\mu_l(u) z\cos u ]+\frac{\mathcal{K}}{\mu_l(u) \cos u}\sinh[\mu_l(u) z\cos u], & z\in[-d,0]\\ \displaystyle \frac{\cosh[\mu_l(u) d\cos u]-\dfrac{\mathcal{K}}{\mu_l(u) \cos u}\sinh[\mu_l(u)d\cos u ]}{\cosh[\mu_l(u)(h-d)]} \cosh[\mu_l(u)(z+h)], & z\in[-h,-d] \end{cases}, \end{align}
\begin{align} &Z_l(z,u)\nonumber\\ &\quad = \begin{cases} \displaystyle \cosh[\mu_l(u) z\cos u ]+\frac{\mathcal{K}}{\mu_l(u) \cos u}\sinh[\mu_l(u) z\cos u], & z\in[-d,0]\\ \displaystyle \frac{\cosh[\mu_l(u) d\cos u]-\dfrac{\mathcal{K}}{\mu_l(u) \cos u}\sinh[\mu_l(u)d\cos u ]}{\cosh[\mu_l(u)(h-d)]} \cosh[\mu_l(u)(z+h)], & z\in[-h,-d] \end{cases}, \end{align}
such that ![]() $\mu =\mu _l(u)$ are solutions of
$\mu =\mu _l(u)$ are solutions of
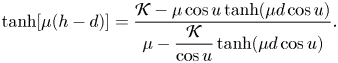 \begin{equation} \tanh[\mu (h-d)]=\frac{\mathcal{K}-\mu \cos u \tanh(\mu d \cos u)}{\mu -\dfrac{\mathcal{K}}{\cos u}\tanh (\mu d \cos u)}. \end{equation}
\begin{equation} \tanh[\mu (h-d)]=\frac{\mathcal{K}-\mu \cos u \tanh(\mu d \cos u)}{\mu -\dfrac{\mathcal{K}}{\cos u}\tanh (\mu d \cos u)}. \end{equation} The roots of (2.16) satisfy ![]() $\mu (-u)=\mu (u)$,
$\mu (-u)=\mu (u)$, ![]() $\mu ({\rm \pi} -u)=\mu (u)$, hence once the roots
$\mu ({\rm \pi} -u)=\mu (u)$, hence once the roots ![]() $\mu (u)$ with
$\mu (u)$ with ![]() $u\in [0, {\rm \pi}/2]$ are known, any other roots with
$u\in [0, {\rm \pi}/2]$ are known, any other roots with ![]() $u\in [-{\rm \pi}, {\rm \pi}]$ can be easily calculated. When
$u\in [-{\rm \pi}, {\rm \pi}]$ can be easily calculated. When ![]() $u=0$ and
$u=0$ and ![]() $\bar {v}=0$, (2.16) becomes
$\bar {v}=0$, (2.16) becomes ![]() $K=\mu \tanh (\mu h)$, which is the dispersion relation in the open sea as expected; when
$K=\mu \tanh (\mu h)$, which is the dispersion relation in the open sea as expected; when ![]() $u={\rm \pi} /2$, it becomes
$u={\rm \pi} /2$, it becomes ![]() $\tanh [\mu (h-d)]={K}/[(1-\bar {v}\ \mathrm{i}-Kd){\mu }]$.
$\tanh [\mu (h-d)]={K}/[(1-\bar {v}\ \mathrm{i}-Kd){\mu }]$.
If ![]() $\mu (u)$ is a root of (2.16),
$\mu (u)$ is a root of (2.16), ![]() $-\mu (u)$ would also be a root. For any specified value of
$-\mu (u)$ would also be a root. For any specified value of ![]() $u$, there is an infinite number of discrete roots of (2.16). These for the cases with
$u$, there is an infinite number of discrete roots of (2.16). These for the cases with ![]() $\bar {v}=0$, in general, consist of two mutually opposite real roots and an infinite sequence of roots lying on the imaginary axis. Since the integral interval of (2.14) is
$\bar {v}=0$, in general, consist of two mutually opposite real roots and an infinite sequence of roots lying on the imaginary axis. Since the integral interval of (2.14) is ![]() $[-{\rm \pi},{\rm \pi} ]$, we need only include the single positive real root,
$[-{\rm \pi},{\rm \pi} ]$, we need only include the single positive real root, ![]() $\mu _0(u)$, and the sequence of roots lying on the positive imaginary axis,
$\mu _0(u)$, and the sequence of roots lying on the positive imaginary axis, ![]() $\mu _l(u)$ for
$\mu _l(u)$ for ![]() $l=1,2,\ldots$, which contribute to propagating and evanescent waves, respectively. An exception is the case with
$l=1,2,\ldots$, which contribute to propagating and evanescent waves, respectively. An exception is the case with ![]() $t={\rm \pi} /2$ and
$t={\rm \pi} /2$ and ![]() $Kd>1$, for which all the roots, including
$Kd>1$, for which all the roots, including ![]() $\mu _0({\rm \pi} /2)$, are imaginary. The roots (2.16) for
$\mu _0({\rm \pi} /2)$, are imaginary. The roots (2.16) for ![]() $\bar {v}\neq 0$ can be derived by using the homotopy method, starting with the corresponding roots for the case of
$\bar {v}\neq 0$ can be derived by using the homotopy method, starting with the corresponding roots for the case of ![]() $\bar {v}=0$ (Meylan, Bennetts & Peter Reference Meylan, Bennetts and Peter2017; Zheng et al. Reference Zheng, Meylan, Fan, Greaves and Iglesias2020a).
$\bar {v}=0$ (Meylan, Bennetts & Peter Reference Meylan, Bennetts and Peter2017; Zheng et al. Reference Zheng, Meylan, Fan, Greaves and Iglesias2020a).
Here ![]() $B_l^{(\,j)}(u)$ could be expressed in terms of any basis whose elements are periodic in
$B_l^{(\,j)}(u)$ could be expressed in terms of any basis whose elements are periodic in ![]() $u$ with period
$u$ with period ![]() $2{\rm \pi}$. Here, we assume that
$2{\rm \pi}$. Here, we assume that ![]() $B_l^{(\,j)}(u)$ may be expressed as
$B_l^{(\,j)}(u)$ may be expressed as
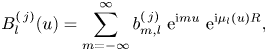 \begin{equation} B_l^{(\,j)}(u)=\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}, \end{equation}
\begin{equation} B_l^{(\,j)}(u)=\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}, \end{equation}
where ![]() $b_{m,l}^{(\,j)}$ are unknown coefficients to be determined, and the exponential factor involving
$b_{m,l}^{(\,j)}$ are unknown coefficients to be determined, and the exponential factor involving ![]() $\mu _l(u)R$ is introduced to suppress numerical rounding error issues otherwise associated with the exponential growth of the functions
$\mu _l(u)R$ is introduced to suppress numerical rounding error issues otherwise associated with the exponential growth of the functions ![]() $J_p(\mu _l(u)R)$ for
$J_p(\mu _l(u)R)$ for ![]() $l >0$ when
$l >0$ when ![]() $\mu _l(u)$ is imaginary. With the employment of (2.17), in place of (2.14), we have
$\mu _l(u)$ is imaginary. With the employment of (2.17), in place of (2.14), we have
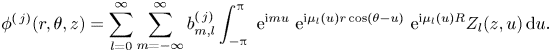 \begin{equation} \phi^{(\,j)}(r,\theta,z)=\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}Z_l(z,u)\,{\rm d}u. \end{equation}
\begin{equation} \phi^{(\,j)}(r,\theta,z)=\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}Z_l(z,u)\,{\rm d}u. \end{equation}With the employment of the Jacobi–Anger expansion of the plane wavefunction
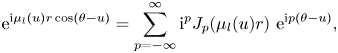 \begin{equation} \mathrm{e}^{\mathrm{i} \mu_l(u) r \cos(\theta-u)}=\sum_{p=-\infty}^{\infty}\mathrm{i}^p J_p(\mu_l(u)r)\ \mathrm{e}^{\mathrm{i} p (\theta-u)}, \end{equation}
\begin{equation} \mathrm{e}^{\mathrm{i} \mu_l(u) r \cos(\theta-u)}=\sum_{p=-\infty}^{\infty}\mathrm{i}^p J_p(\mu_l(u)r)\ \mathrm{e}^{\mathrm{i} p (\theta-u)}, \end{equation}the velocity potential at the interior region can be further expressed as
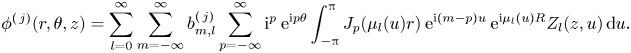 \begin{equation} \phi^{(\,j)}(r,\theta,z)=\sum_{l=0}^{\infty} \sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\sum_{p=-\infty}^{\infty}\mathrm{i}^p \ \mathrm{e}^{\mathrm{i} p \theta} \int_{-{\rm \pi}}^{\rm \pi}J_p(\mu_l(u)r)\ \mathrm{e}^{\mathrm{i} (m-p) u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}Z_l(z,u)\,{\rm d}u. \end{equation}
\begin{equation} \phi^{(\,j)}(r,\theta,z)=\sum_{l=0}^{\infty} \sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\sum_{p=-\infty}^{\infty}\mathrm{i}^p \ \mathrm{e}^{\mathrm{i} p \theta} \int_{-{\rm \pi}}^{\rm \pi}J_p(\mu_l(u)r)\ \mathrm{e}^{\mathrm{i} (m-p) u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}Z_l(z,u)\,{\rm d}u. \end{equation}2.3. Solution of the unknown coefficients
The unknown coefficients ![]() $a_{m,l}^{(\,j)}$ and
$a_{m,l}^{(\,j)}$ and ![]() $b_{m,l}^{(\,j)}$ can be determined by using the continuity conditions of the velocity potential and mass fluxes at the interface between the interior and exterior regions.
$b_{m,l}^{(\,j)}$ can be determined by using the continuity conditions of the velocity potential and mass fluxes at the interface between the interior and exterior regions.
Applying the continuity condition of the velocity potential at ![]() $r=R$, i.e.
$r=R$, i.e. ![]() $\phi ^{(\,j)}(R^-,\theta,z)=\phi ^{(\,j)}(R^+,\theta,z)$ all over the water depth gives
$\phi ^{(\,j)}(R^-,\theta,z)=\phi ^{(\,j)}(R^+,\theta,z)$ all over the water depth gives
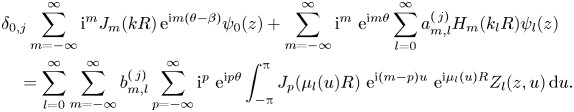 \begin{align} &\delta_{0,j}\sum_{m=-\infty}^{\infty}\mathrm{i}^m J_m(k R)\, \mathrm{e}^{\mathrm{i} m (\theta-\beta)}\psi_0(z)+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \ \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}H_m(k_l R)\psi_l(z)\nonumber\\ &\quad =\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)} \sum_{p=-\infty}^{\infty}\mathrm{i}^p \ \mathrm{e}^{\mathrm{i} p \theta} \int_{-{\rm \pi}}^{\rm \pi}J_p(\mu_l(u)R)\ \mathrm{e}^{\mathrm{i} (m-p) u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}Z_l(z,u)\,{\rm d}u. \end{align}
\begin{align} &\delta_{0,j}\sum_{m=-\infty}^{\infty}\mathrm{i}^m J_m(k R)\, \mathrm{e}^{\mathrm{i} m (\theta-\beta)}\psi_0(z)+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \ \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}H_m(k_l R)\psi_l(z)\nonumber\\ &\quad =\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)} \sum_{p=-\infty}^{\infty}\mathrm{i}^p \ \mathrm{e}^{\mathrm{i} p \theta} \int_{-{\rm \pi}}^{\rm \pi}J_p(\mu_l(u)R)\ \mathrm{e}^{\mathrm{i} (m-p) u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}Z_l(z,u)\,{\rm d}u. \end{align} After multiplying both sides by ![]() $\psi _s(z)\ \mathrm{e}^{-\mathrm {i} q \theta }$, integrating in
$\psi _s(z)\ \mathrm{e}^{-\mathrm {i} q \theta }$, integrating in ![]() $z\in [-h, 0]$ and
$z\in [-h, 0]$ and ![]() $\theta \in [0, 2{\rm \pi} ]$, and using their orthogonality characteristics, it can be rewritten as
$\theta \in [0, 2{\rm \pi} ]$, and using their orthogonality characteristics, it can be rewritten as
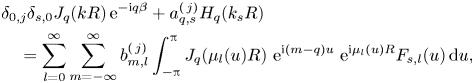 \begin{align} &\delta_{0,j}\delta_{s,0} J_{q}(k R)\, \mathrm{e}^{-\mathrm{i} q \beta}+ a_{{q},s}^{(\,j)}H_{q}(k_{s}R)\nonumber\\ &\quad =\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty} b_{m,l}^{(\,j)} \int_{-{\rm \pi}}^{\rm \pi}J_{q}(\mu_l(u)R)\ \mathrm{e}^{\mathrm{i} (m-{q}) u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}F_{s,l}(u)\,{\rm d}u, \end{align}
\begin{align} &\delta_{0,j}\delta_{s,0} J_{q}(k R)\, \mathrm{e}^{-\mathrm{i} q \beta}+ a_{{q},s}^{(\,j)}H_{q}(k_{s}R)\nonumber\\ &\quad =\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty} b_{m,l}^{(\,j)} \int_{-{\rm \pi}}^{\rm \pi}J_{q}(\mu_l(u)R)\ \mathrm{e}^{\mathrm{i} (m-{q}) u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}F_{s,l}(u)\,{\rm d}u, \end{align}where
in which
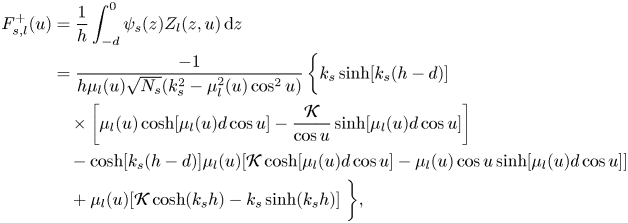 \begin{align} F_{s,l}^+(u)&=\frac{1}{h}\int_{-d}^0 \psi_{s}(z)Z_l(z,u)\,{\rm d} z\nonumber\\ &=\frac{-1}{h\mu_l(u)\sqrt{N_{s}}(k_{s}^2-\mu_l^2(u)\cos^2u)}\left\{k_{s} \sinh[k_{s}(h-d)]\vphantom{\frac{\mathcal{K}}{\cos u}}\right.\nonumber\\ &\quad\times\left[\mu_l(u)\cosh[\mu_l(u) d\cos u]-\frac{\mathcal{K}}{\cos u}\sinh[\mu_l(u)d\cos u ]\right]\nonumber\\ &\quad-\cosh[k_{s}(h-d)]\mu_l(u)[\mathcal{K}\cosh[\mu_l(u)d\cos u]-\mu_l(u)\cos u \sinh[\mu_l(u)d\cos u]]\nonumber\\ &\quad+\mu_l(u)[\mathcal{K} \cosh(k_{s}h)-k_{s}\sinh(k_{s}h)]\left.\vphantom{\frac{\mathcal{K}}{\cos u}}\right\}\!, \end{align}
\begin{align} F_{s,l}^+(u)&=\frac{1}{h}\int_{-d}^0 \psi_{s}(z)Z_l(z,u)\,{\rm d} z\nonumber\\ &=\frac{-1}{h\mu_l(u)\sqrt{N_{s}}(k_{s}^2-\mu_l^2(u)\cos^2u)}\left\{k_{s} \sinh[k_{s}(h-d)]\vphantom{\frac{\mathcal{K}}{\cos u}}\right.\nonumber\\ &\quad\times\left[\mu_l(u)\cosh[\mu_l(u) d\cos u]-\frac{\mathcal{K}}{\cos u}\sinh[\mu_l(u)d\cos u ]\right]\nonumber\\ &\quad-\cosh[k_{s}(h-d)]\mu_l(u)[\mathcal{K}\cosh[\mu_l(u)d\cos u]-\mu_l(u)\cos u \sinh[\mu_l(u)d\cos u]]\nonumber\\ &\quad+\mu_l(u)[\mathcal{K} \cosh(k_{s}h)-k_{s}\sinh(k_{s}h)]\left.\vphantom{\frac{\mathcal{K}}{\cos u}}\right\}\!, \end{align}and
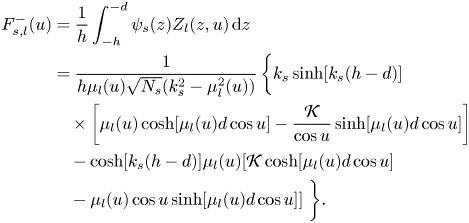 \begin{align}
F_{s,l}^-(u)&=\frac{1}{h}\int_{-h}^{-d}
\psi_{s}(z)Z_l(z,u)\,{\rm d} z\nonumber\\
&=\frac{1}{h\mu_l(u)\sqrt{N_{s}}(k_{s}^2-\mu_l^2(u))}\left\{k_{s}
\sinh[k_{s}(h-d)]\vphantom{\frac{\mathcal{K}}{\cos
u}}\right.\nonumber\\
&\quad\times\left[\mu_l(u)\cosh[\mu_l(u) d\cos
u]-\frac{\mathcal{K}}{\cos u}\sinh[\mu_l(u)d\cos u
]\right]\nonumber\\
&\quad-\cosh[k_{s}(h-d)]\mu_l(u)[\mathcal{K}\cosh[\mu_l(u)d\cos
u]\nonumber\\ &\quad -\mu_l(u)\cos u \sinh[\mu_l(u)d\cos
u]]\left.\vphantom{\frac{\mathcal{K}}{\cos u}}\right\}\!.
\end{align}
\begin{align}
F_{s,l}^-(u)&=\frac{1}{h}\int_{-h}^{-d}
\psi_{s}(z)Z_l(z,u)\,{\rm d} z\nonumber\\
&=\frac{1}{h\mu_l(u)\sqrt{N_{s}}(k_{s}^2-\mu_l^2(u))}\left\{k_{s}
\sinh[k_{s}(h-d)]\vphantom{\frac{\mathcal{K}}{\cos
u}}\right.\nonumber\\
&\quad\times\left[\mu_l(u)\cosh[\mu_l(u) d\cos
u]-\frac{\mathcal{K}}{\cos u}\sinh[\mu_l(u)d\cos u
]\right]\nonumber\\
&\quad-\cosh[k_{s}(h-d)]\mu_l(u)[\mathcal{K}\cosh[\mu_l(u)d\cos
u]\nonumber\\ &\quad -\mu_l(u)\cos u \sinh[\mu_l(u)d\cos
u]]\left.\vphantom{\frac{\mathcal{K}}{\cos u}}\right\}\!.
\end{align} The continuity condition of the velocity at ![]() $r=R$, i.e. (2.8b) for
$r=R$, i.e. (2.8b) for ![]() $z\in [-d,0]$ and
$z\in [-d,0]$ and ![]() ${\partial \phi ^{(\,j)}}/{\partial r}|_{r=R^-}={\partial \phi ^{(\,j)}}/{\partial r}|_{r=R^+}$ for
${\partial \phi ^{(\,j)}}/{\partial r}|_{r=R^-}={\partial \phi ^{(\,j)}}/{\partial r}|_{r=R^+}$ for ![]() $z\in [-h,-d]$, gives
$z\in [-h,-d]$, gives
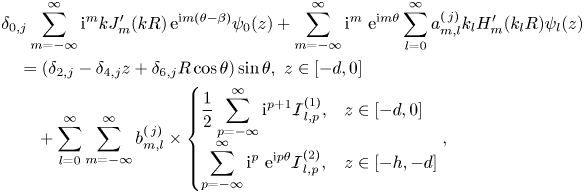 \begin{align} &\delta_{0,j}\sum_{m=-\infty}^{\infty}\mathrm{i}^m k J'_m(k R)\, \mathrm{e}^{\mathrm{i} m (\theta-\beta)}\psi_0(z)+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \ \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}k_l H'_m(k_l R)\psi_l(z)\nonumber\\ &\quad =(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos \theta) \sin \theta,\,\,z\in[-d,0]\nonumber\\ &\qquad +\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\times \begin{cases} \displaystyle \frac{1}{2}\sum_{p=-\infty}^{\infty}\mathrm{i}^{p+1} \mathcal{I}^{(1)}_{l,p} , & z\in[-d,0]\\ \displaystyle \sum_{p=-\infty}^{\infty}\mathrm{i}^p \ \mathrm{e}^{\mathrm{i} p \theta} \mathcal{I}^{(2)}_{l,p}, & z\in[-h,-d] \end{cases}, \end{align}
\begin{align} &\delta_{0,j}\sum_{m=-\infty}^{\infty}\mathrm{i}^m k J'_m(k R)\, \mathrm{e}^{\mathrm{i} m (\theta-\beta)}\psi_0(z)+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \ \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}k_l H'_m(k_l R)\psi_l(z)\nonumber\\ &\quad =(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos \theta) \sin \theta,\,\,z\in[-d,0]\nonumber\\ &\qquad +\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\times \begin{cases} \displaystyle \frac{1}{2}\sum_{p=-\infty}^{\infty}\mathrm{i}^{p+1} \mathcal{I}^{(1)}_{l,p} , & z\in[-d,0]\\ \displaystyle \sum_{p=-\infty}^{\infty}\mathrm{i}^p \ \mathrm{e}^{\mathrm{i} p \theta} \mathcal{I}^{(2)}_{l,p}, & z\in[-h,-d] \end{cases}, \end{align}with
and
After multiplying both sides by ![]() $\psi _s(z)\ \mathrm{e}^{-\mathrm {i} q\theta }$, integrating in
$\psi _s(z)\ \mathrm{e}^{-\mathrm {i} q\theta }$, integrating in ![]() $z\in [-h, 0]$ and
$z\in [-h, 0]$ and ![]() $\theta \in [0, 2{\rm \pi} ]$, and using their orthogonality characteristics, it can be rewritten as
$\theta \in [0, 2{\rm \pi} ]$, and using their orthogonality characteristics, it can be rewritten as
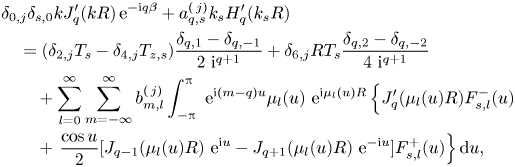 \begin{align} &\delta_{0,j}\delta_{{s},0} k J'_{q}(k R)\, \mathrm{e}^{-\mathrm{i} {q} \beta}+ a_{{q},{s}}^{(\,j)}k_{s}H'_{q}(k_{s}R)\nonumber\\ &\quad =(\delta_{2,j}T_{s}-\delta_{4,j}T_{z,{s}}) \frac{\delta_{q,1}-\delta_{{q},-1}}{2\ \mathrm{i}^{{q}+1}}+\delta_{6,j}R T_{s}\frac{\delta_{{q},2}-\delta_{{q},-2}}{4\ \mathrm{i}^{{q}+1}}\nonumber\\ &\qquad+\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)} \int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} (m-{q}) u}\mu_l(u)\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}\left\{ J'_{q}(\mu_l(u)R)F_{{s},l}^-(u)\vphantom{\frac{\cos u}{2}}\right.\nonumber\\ &\qquad+\left.\frac{\cos u}{2}[J_{q-1}(\mu_l(u)R)\ \mathrm{e}^{\mathrm{i} u}-J_{{q}+1}(\mu_l(u)R)\ \mathrm{e}^{-\mathrm{i} u}] F_{s,l}^+(u)\right\} {\rm d}u, \end{align}
\begin{align} &\delta_{0,j}\delta_{{s},0} k J'_{q}(k R)\, \mathrm{e}^{-\mathrm{i} {q} \beta}+ a_{{q},{s}}^{(\,j)}k_{s}H'_{q}(k_{s}R)\nonumber\\ &\quad =(\delta_{2,j}T_{s}-\delta_{4,j}T_{z,{s}}) \frac{\delta_{q,1}-\delta_{{q},-1}}{2\ \mathrm{i}^{{q}+1}}+\delta_{6,j}R T_{s}\frac{\delta_{{q},2}-\delta_{{q},-2}}{4\ \mathrm{i}^{{q}+1}}\nonumber\\ &\qquad+\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)} \int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} (m-{q}) u}\mu_l(u)\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}\left\{ J'_{q}(\mu_l(u)R)F_{{s},l}^-(u)\vphantom{\frac{\cos u}{2}}\right.\nonumber\\ &\qquad+\left.\frac{\cos u}{2}[J_{q-1}(\mu_l(u)R)\ \mathrm{e}^{\mathrm{i} u}-J_{{q}+1}(\mu_l(u)R)\ \mathrm{e}^{-\mathrm{i} u}] F_{s,l}^+(u)\right\} {\rm d}u, \end{align}where
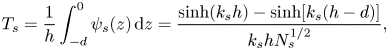 \begin{equation} T_{s}= \frac{1}{h}\int_{-d}^0 \psi_{s}(z) \,{\rm d}z= \frac{\sinh(k_{s}h)-\sinh[k_{s}(h-d)]}{k_{s}hN_{s}^{{1/2}}}, \end{equation}
\begin{equation} T_{s}= \frac{1}{h}\int_{-d}^0 \psi_{s}(z) \,{\rm d}z= \frac{\sinh(k_{s}h)-\sinh[k_{s}(h-d)]}{k_{s}hN_{s}^{{1/2}}}, \end{equation}and
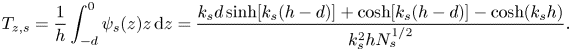 \begin{equation} T_{z,{s}}= \frac{1}{h}\int_{-d}^0 \psi_{s}(z)z \,{\rm d}z=\frac{k_{s} d\sinh[k_{s}(h-d)]+\cosh[k_{s} (h-d)]-\cosh(k_{s}h)}{k_{s}^2 h N_{s}^{{1/2}}}. \end{equation}
\begin{equation} T_{z,{s}}= \frac{1}{h}\int_{-d}^0 \psi_{s}(z)z \,{\rm d}z=\frac{k_{s} d\sinh[k_{s}(h-d)]+\cosh[k_{s} (h-d)]-\cosh(k_{s}h)}{k_{s}^2 h N_{s}^{{1/2}}}. \end{equation}After combining (2.22) and (2.29), and applying the Wronksian identity for Bessel functions (Abramowitz & Stegun Reference Abramowitz and Stegun1964),
we have the following matrix equation to determine the unknown coefficients ![]() $b_{m,l}^{(\,j)}$:
$b_{m,l}^{(\,j)}$:
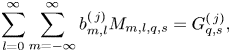 \begin{equation} \sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}M_{m,l,q,s}=G_{q,s}^{(\,j)}, \end{equation}
\begin{equation} \sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}M_{m,l,q,s}=G_{q,s}^{(\,j)}, \end{equation}in which
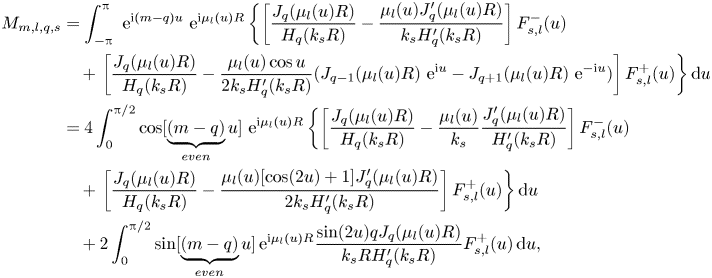 \begin{align}
M_{m,l,q,s}&=\int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i}
(m-{q}) u}\ \mathrm{e}^{\mathrm{i}
\mu_l(u)R}\left\{\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}R)}-
\frac{\mu_l(u)J'_{q}(\mu_l(u)R)}{k_{s}H'_{q}(k_{s}R)}\right]
F_{{s},l}^-(u)\right.\nonumber\\ &\quad
+\left.\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}R)}-\frac{\mu_l(u)
\cos u}{2k_{s}H'_{q}(k_{s}R)}(J_{q-1}(\mu_l(u)R)\
\mathrm{e}^{\mathrm{i} u}-J_{q+1}(\mu_l(u)R)\
\mathrm{e}^{-\mathrm{i} u})\right]F_{s,l}^+(u)\right\} {\rm
d}u\nonumber\\
&=4\int_{0}^{{\rm \pi}/{2}}\cos[\underbrace{(m-{q})}_{even}u]\
\mathrm{e}^{\mathrm{i}
\mu_l(u)R}\left\{\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}R)}-
\frac{\mu_l(u)}{k_{s}}\frac{J'_{q}(\mu_l(u)R)}{H'_{q}(k_{s}R)}
\right]F_{{s},l}^-(u)\right.\nonumber\\ &\quad
+\left.\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}
R)}-\frac{\mu_l(u)[\cos(2u)+1]J'_{q}(\mu_l(u)R)}{2 k_{s}
H'_{q}(k_{s}R)} \right]F_{{s},l}^+(u)\right\} {\rm d}
u\nonumber\\ &\quad
+2\int_{0}^{{\rm \pi}/{2}}\sin[\underbrace{(m-{q})}_{even}u]\,
\mathrm{e}^{\mathrm{i} \mu_l(u)R}\frac{\sin(2u)
{q}J_{q}(\mu_l(u)R)}{k_{s} R
H'_{q}(k_{s}R)}F_{{s},l}^+(u)\,{\rm d} u,
\end{align}
\begin{align}
M_{m,l,q,s}&=\int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i}
(m-{q}) u}\ \mathrm{e}^{\mathrm{i}
\mu_l(u)R}\left\{\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}R)}-
\frac{\mu_l(u)J'_{q}(\mu_l(u)R)}{k_{s}H'_{q}(k_{s}R)}\right]
F_{{s},l}^-(u)\right.\nonumber\\ &\quad
+\left.\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}R)}-\frac{\mu_l(u)
\cos u}{2k_{s}H'_{q}(k_{s}R)}(J_{q-1}(\mu_l(u)R)\
\mathrm{e}^{\mathrm{i} u}-J_{q+1}(\mu_l(u)R)\
\mathrm{e}^{-\mathrm{i} u})\right]F_{s,l}^+(u)\right\} {\rm
d}u\nonumber\\
&=4\int_{0}^{{\rm \pi}/{2}}\cos[\underbrace{(m-{q})}_{even}u]\
\mathrm{e}^{\mathrm{i}
\mu_l(u)R}\left\{\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}R)}-
\frac{\mu_l(u)}{k_{s}}\frac{J'_{q}(\mu_l(u)R)}{H'_{q}(k_{s}R)}
\right]F_{{s},l}^-(u)\right.\nonumber\\ &\quad
+\left.\left[\frac{J_{q}(\mu_l(u)R)}{H_{q}(k_{s}
R)}-\frac{\mu_l(u)[\cos(2u)+1]J'_{q}(\mu_l(u)R)}{2 k_{s}
H'_{q}(k_{s}R)} \right]F_{{s},l}^+(u)\right\} {\rm d}
u\nonumber\\ &\quad
+2\int_{0}^{{\rm \pi}/{2}}\sin[\underbrace{(m-{q})}_{even}u]\,
\mathrm{e}^{\mathrm{i} \mu_l(u)R}\frac{\sin(2u)
{q}J_{q}(\mu_l(u)R)}{k_{s} R
H'_{q}(k_{s}R)}F_{{s},l}^+(u)\,{\rm d} u,
\end{align}and
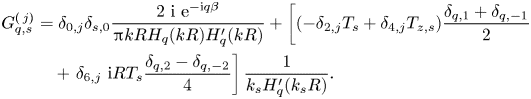 \begin{align} G_{{q},{s}}^{(\,j)}&= \delta_{0,j}\delta_{{s},0} \frac{2\ \mathrm{i} \ \mathrm{e}^{-\mathrm{i} {q} \beta}}{{\rm \pi} k R H_{q}(kR) H'_{q}(kR)}+ \left[(-\delta_{2,j}T_{s}+\delta_{4,j}T_{z,{s}}) \frac{\delta_{q,1}+\delta_{q,-1}}{2}\right.\nonumber\\ &\quad+\left.\delta_{6,j}\ \mathrm{i} R T_{s}\frac{\delta_{{q},2}-\delta_{q,-2}}{4}\right]\frac{1}{k_{s} H_{q}'(k_{s} R)}. \end{align}
\begin{align} G_{{q},{s}}^{(\,j)}&= \delta_{0,j}\delta_{{s},0} \frac{2\ \mathrm{i} \ \mathrm{e}^{-\mathrm{i} {q} \beta}}{{\rm \pi} k R H_{q}(kR) H'_{q}(kR)}+ \left[(-\delta_{2,j}T_{s}+\delta_{4,j}T_{z,{s}}) \frac{\delta_{q,1}+\delta_{q,-1}}{2}\right.\nonumber\\ &\quad+\left.\delta_{6,j}\ \mathrm{i} R T_{s}\frac{\delta_{{q},2}-\delta_{q,-2}}{4}\right]\frac{1}{k_{s} H_{q}'(k_{s} R)}. \end{align} Once ![]() $b_{m,l}^{(\,j)}$ are known,
$b_{m,l}^{(\,j)}$ are known, ![]() $a_{m,l}^{(\,j)}$ can be further determined with the employment of (2.22).
$a_{m,l}^{(\,j)}$ can be further determined with the employment of (2.22).
3. Hydrodynamic responses and reciprocal relations
3.1. Free surface elevation
The complex amplitude of the free surface elevation associated with ![]() $\phi ^{(\,j)}$ is
$\phi ^{(\,j)}$ is
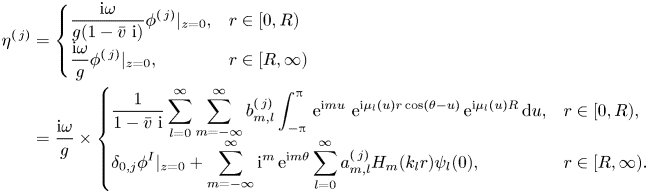 \begin{align} \eta^{(\,j)}&=\begin{cases} \displaystyle \frac{\mathrm{i}\omega}{g(1-\bar{v}\ \mathrm{i})}\phi^{(\,j)}|_{z=0}, & r\in[0,R)\\ \displaystyle \frac{\mathrm{i}\omega}{g}\phi^{(\,j)}|_{z=0}, & {r\in[R,\infty)} \end{cases}\nonumber\\ & =\frac{\mathrm{i}\omega}{g}\times \begin{cases} \displaystyle {\frac{1}{1-\bar{v}\ \mathrm{i}}}\sum_{l=0}^{\infty} \sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{-{\rm \pi}}^{\rm \pi}\, \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\, \mathrm{e}^{\mathrm{i} \mu_l(u)R}\,{\rm d}u, & r\in[0,R),\\ \displaystyle \delta_{0,j} \phi^I|_{z=0}+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \, \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}H_m(k_l r)\psi_l(0), & r\in[R,\infty). \end{cases} \end{align}
\begin{align} \eta^{(\,j)}&=\begin{cases} \displaystyle \frac{\mathrm{i}\omega}{g(1-\bar{v}\ \mathrm{i})}\phi^{(\,j)}|_{z=0}, & r\in[0,R)\\ \displaystyle \frac{\mathrm{i}\omega}{g}\phi^{(\,j)}|_{z=0}, & {r\in[R,\infty)} \end{cases}\nonumber\\ & =\frac{\mathrm{i}\omega}{g}\times \begin{cases} \displaystyle {\frac{1}{1-\bar{v}\ \mathrm{i}}}\sum_{l=0}^{\infty} \sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{-{\rm \pi}}^{\rm \pi}\, \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\, \mathrm{e}^{\mathrm{i} \mu_l(u)R}\,{\rm d}u, & r\in[0,R),\\ \displaystyle \delta_{0,j} \phi^I|_{z=0}+\sum_{m=-\infty}^{\infty}\mathrm{i}^m \, \mathrm{e}^{\mathrm{i} m \theta}\sum_{l=0}^{\infty}a_{m,l}^{(\,j)}H_m(k_l r)\psi_l(0), & r\in[R,\infty). \end{cases} \end{align}3.2. Wave excitation forces and wave radiation forces
The wave excitation and radiation forces acting on the structured cylinder is a sum over all of the vertical barriers of the differential pressure induced by the scattered waves and radiated waves, respectively, acting over each barrier. It is straightforward to determine the effective medium limit of this discrete description which results in the expression
where ![]() $V_c$ denotes the volume domain occupied by the truncated metamaterial cylinder, i.e.
$V_c$ denotes the volume domain occupied by the truncated metamaterial cylinder, i.e. ![]() $r\in [0,R], \theta \in [0,2{\rm \pi} ], z\in [-d,0]$. Here
$r\in [0,R], \theta \in [0,2{\rm \pi} ], z\in [-d,0]$. Here ![]() $F_{ij}$ for
$F_{ij}$ for ![]() $j=0$ denotes the wave excitation force acting on the cylinder in the
$j=0$ denotes the wave excitation force acting on the cylinder in the ![]() $i$th mode; for
$i$th mode; for ![]() $j\neq 0$, it denotes the wave radiation force acting on the cylinder in
$j\neq 0$, it denotes the wave radiation force acting on the cylinder in ![]() $i$th mode due to a unit amplitude velocity oscillation of the cylinder in
$i$th mode due to a unit amplitude velocity oscillation of the cylinder in ![]() $j$th mode in still water. Here
$j$th mode in still water. Here ![]() $a_{ij}^{(0)}$ is the effective mass of the water occupied by the metamaterial cylinder to account for their inertial effect which is not reflected in the velocity potential for the wave radiation problem. We have
$a_{ij}^{(0)}$ is the effective mass of the water occupied by the metamaterial cylinder to account for their inertial effect which is not reflected in the velocity potential for the wave radiation problem. We have ![]() $a_{22}^{(0)}=\rho {\rm \pi}R^2 d$,
$a_{22}^{(0)}=\rho {\rm \pi}R^2 d$, ![]() $a_{44}^{(0)}=\rho {\rm \pi}R^2 d^3/3$,
$a_{44}^{(0)}=\rho {\rm \pi}R^2 d^3/3$, ![]() $a_{66}^{(0)}=\rho {\rm \pi}R^4 d/4$,
$a_{66}^{(0)}=\rho {\rm \pi}R^4 d/4$, ![]() $a_{24}^{(0)}=a_{42}^{(0)}=\rho {\rm \pi}R^2 d^2/2$ and a vanishing
$a_{24}^{(0)}=a_{42}^{(0)}=\rho {\rm \pi}R^2 d^2/2$ and a vanishing ![]() $a_{ij}^{(0)}$ for other
$a_{ij}^{(0)}$ for other ![]() $i,j$. The wave radiation force (i.e.
$i,j$. The wave radiation force (i.e. ![]() $F_{ij}$ for
$F_{ij}$ for ![]() $j\neq 0$) can be further expressed as
$j\neq 0$) can be further expressed as ![]() $F_{ij}=-c_{ij}+\mathrm {i} \omega a_{ij}$, where
$F_{ij}=-c_{ij}+\mathrm {i} \omega a_{ij}$, where ![]() $c_{ij}$ and
$c_{ij}$ and ![]() $a_{ij}$ are the so-called wave radiation damping and added mass, respectively.
$a_{ij}$ are the so-called wave radiation damping and added mass, respectively.
From another point of view, after applying the divergence theorem, also known as Gauss' theorem, ![]() $F_{ij}$ may be rewritten as
$F_{ij}$ may be rewritten as
where ![]() $S_c$ denotes the curved sidewall of the truncated metamaterial cylinder, i.e.
$S_c$ denotes the curved sidewall of the truncated metamaterial cylinder, i.e. ![]() $r=R, \theta \in [0,2{\rm \pi} ], z\in [-d,0]$. Compared with (3.2), (3.3) is simpler because of no partial derivative in
$r=R, \theta \in [0,2{\rm \pi} ], z\in [-d,0]$. Compared with (3.2), (3.3) is simpler because of no partial derivative in ![]() $y$ direction and one less integral over
$y$ direction and one less integral over ![]() $r\in [0,R]$.
$r\in [0,R]$.
After applying the expression of the velocity potential at the interior region, i.e. (2.20), both (3.2) and (3.3) give the same expression of ![]() $F_{ij}$:
$F_{ij}$:
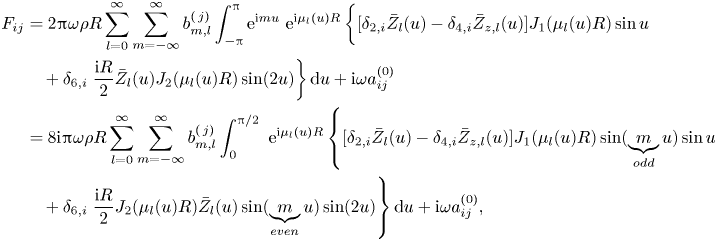 \begin{align} F_{ij}&=2 {\rm \pi}\omega \rho R \sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{-{\rm \pi}}^{\rm \pi} \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R} \left\{[\delta_{2,i}\bar{Z}_l(u)-\delta_{4,i}\bar{Z}_{z,l}(u)]J_1(\mu_l(u)R)\sin u \vphantom{\frac{\mathrm{i} R}{2}}\right.\nonumber\\ &\quad +\delta_{6,i}\left.\frac{\mathrm{i} R}{2}\bar{Z}_l(u)J_2(\mu_l(u)R) \sin(2u)\right\} {\rm d}u+\mathrm{i} \omega a_{ij}^{(0)}\nonumber\\ &=8 \mathrm{i} {\rm \pi}\omega \rho R \sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{0}^{{\rm \pi}/{2}} \ \mathrm{e}^{\mathrm{i} \mu_l(u)R} \left\{[\delta_{2,i}\bar{Z}_l(u)-\delta_{4,i}\bar{Z}_{z,l}(u)] J_1(\mu_l(u)R)\sin(\underbrace{m}_{odd}u)\sin u\vphantom{\frac{\mathrm{i} R}{2}}\right.\nonumber\\ &\quad +\delta_{6,i}\left.\frac{\mathrm{i} R}{2}J_2(\mu_l(u)R)\bar{Z}_l(u)\sin(\underbrace{m}_{even}u)\sin (2u)\right\} {\rm d}u +\mathrm{i} \omega a_{ij}^{(0)}, \end{align}
\begin{align} F_{ij}&=2 {\rm \pi}\omega \rho R \sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{-{\rm \pi}}^{\rm \pi} \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R} \left\{[\delta_{2,i}\bar{Z}_l(u)-\delta_{4,i}\bar{Z}_{z,l}(u)]J_1(\mu_l(u)R)\sin u \vphantom{\frac{\mathrm{i} R}{2}}\right.\nonumber\\ &\quad +\delta_{6,i}\left.\frac{\mathrm{i} R}{2}\bar{Z}_l(u)J_2(\mu_l(u)R) \sin(2u)\right\} {\rm d}u+\mathrm{i} \omega a_{ij}^{(0)}\nonumber\\ &=8 \mathrm{i} {\rm \pi}\omega \rho R \sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(\,j)}\int_{0}^{{\rm \pi}/{2}} \ \mathrm{e}^{\mathrm{i} \mu_l(u)R} \left\{[\delta_{2,i}\bar{Z}_l(u)-\delta_{4,i}\bar{Z}_{z,l}(u)] J_1(\mu_l(u)R)\sin(\underbrace{m}_{odd}u)\sin u\vphantom{\frac{\mathrm{i} R}{2}}\right.\nonumber\\ &\quad +\delta_{6,i}\left.\frac{\mathrm{i} R}{2}J_2(\mu_l(u)R)\bar{Z}_l(u)\sin(\underbrace{m}_{even}u)\sin (2u)\right\} {\rm d}u +\mathrm{i} \omega a_{ij}^{(0)}, \end{align}where
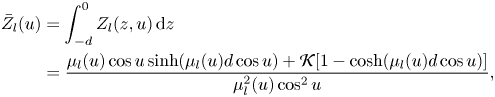 \begin{align} \bar{Z}_l(u)&= \int_{-d}^{0} {Z}_l(z,u)\,{\rm d} z\nonumber\\ &=\frac{\mu_l(u)\cos u \sinh(\mu_l(u)d\cos u)+\mathcal{K}[1-\cosh(\mu_l(u) d\cos u)]}{\mu_l^2(u) \cos^2 u}, \end{align}
\begin{align} \bar{Z}_l(u)&= \int_{-d}^{0} {Z}_l(z,u)\,{\rm d} z\nonumber\\ &=\frac{\mu_l(u)\cos u \sinh(\mu_l(u)d\cos u)+\mathcal{K}[1-\cosh(\mu_l(u) d\cos u)]}{\mu_l^2(u) \cos^2 u}, \end{align}and
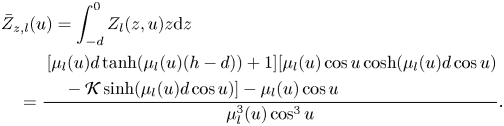 \begin{align} &\bar{Z}_{z,l}(u)= \int_{-d}^{0} {Z}_l(z,u)z{\rm d} z\nonumber\\ &\quad =\frac{\begin{aligned} & [\mu_l(u)d \tanh(\mu_l(u)(h-d))+1] [\mu_l(u) \cos u \cosh(\mu_l(u)d \cos u)\\ & \quad-\mathcal{K}\sinh(\mu_l(u)d \cos u)]-\mu_l(u) \cos u \end{aligned}}{\mu_l^3(u) \cos^3 u}. \end{align}
\begin{align} &\bar{Z}_{z,l}(u)= \int_{-d}^{0} {Z}_l(z,u)z{\rm d} z\nonumber\\ &\quad =\frac{\begin{aligned} & [\mu_l(u)d \tanh(\mu_l(u)(h-d))+1] [\mu_l(u) \cos u \cosh(\mu_l(u)d \cos u)\\ & \quad-\mathcal{K}\sinh(\mu_l(u)d \cos u)]-\mu_l(u) \cos u \end{aligned}}{\mu_l^3(u) \cos^3 u}. \end{align} Note that ![]() $\phi ^{(\,j)}|_{r=R^-}=\phi ^{(\,j)}|_{r=R^+}$, hence (3.3) can be rewritten in terms of the velocity potential at the exterior region
$\phi ^{(\,j)}|_{r=R^-}=\phi ^{(\,j)}|_{r=R^+}$, hence (3.3) can be rewritten in terms of the velocity potential at the exterior region
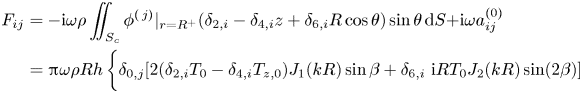 \begin{align} F_{ij}&=-\mathrm{i} \omega \rho \iint_{S_c}\phi^{(\,j)}|_{r=R^+}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta) \sin \theta \,{\rm d} S{+\mathrm{i} \omega a_{ij}^{(0)}}\nonumber\\ &={\rm \pi} \omega \rho R h \left\{ \delta_{0,j}[2(\delta_{2,i}T_0-\delta_{4,i}T_{z,0}) J_{1}(k R) \sin \beta+ \delta_{6,i}\ \mathrm{i} R T_0 J_{2}(k R)\sin (2\beta)]\vphantom{\frac{\mathrm{i} R}{2}}\right. \nonumber\\ & \quad + \mathrm{i}\sum_{l=0}^{\infty}\left.\left[(\delta_{2,i}T_l-\delta_{4,i}T_{z,l}) (a_{1,l}^{(\,j)}-a_{-1,l}^{(\,j)})H_{1}(k_l R)+\delta_{6,i}\frac{\mathrm{i} R}{2}(a_{2,l}^{(\,j)}-a_{-2,l}^{(\,j)})H_{2}(k_l R)T_l\right]\right\}\nonumber\\ &\quad +\mathrm{i} \omega a_{ij}^{(0)}, \end{align}
\begin{align} F_{ij}&=-\mathrm{i} \omega \rho \iint_{S_c}\phi^{(\,j)}|_{r=R^+}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta) \sin \theta \,{\rm d} S{+\mathrm{i} \omega a_{ij}^{(0)}}\nonumber\\ &={\rm \pi} \omega \rho R h \left\{ \delta_{0,j}[2(\delta_{2,i}T_0-\delta_{4,i}T_{z,0}) J_{1}(k R) \sin \beta+ \delta_{6,i}\ \mathrm{i} R T_0 J_{2}(k R)\sin (2\beta)]\vphantom{\frac{\mathrm{i} R}{2}}\right. \nonumber\\ & \quad + \mathrm{i}\sum_{l=0}^{\infty}\left.\left[(\delta_{2,i}T_l-\delta_{4,i}T_{z,l}) (a_{1,l}^{(\,j)}-a_{-1,l}^{(\,j)})H_{1}(k_l R)+\delta_{6,i}\frac{\mathrm{i} R}{2}(a_{2,l}^{(\,j)}-a_{-2,l}^{(\,j)})H_{2}(k_l R)T_l\right]\right\}\nonumber\\ &\quad +\mathrm{i} \omega a_{ij}^{(0)}, \end{align}
which is much simpler than (3.4) because of the absence of the integration over ![]() $t\in [0,{\rm \pi} /2]$ and the accumulation over
$t\in [0,{\rm \pi} /2]$ and the accumulation over ![]() $m\in (-\infty,\infty )$.
$m\in (-\infty,\infty )$.
3.3. Far-field radiation coefficient
For wave radiation problems, as ![]() $kr\rightarrow \infty$, after applying the large argument asymptotics of the Hankel function, we have
$kr\rightarrow \infty$, after applying the large argument asymptotics of the Hankel function, we have
where
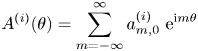 \begin{equation} A^{(i)}(\theta)=\sum_{m=-\infty}^{\infty}a_{m,0}^{(i)}\ \mathrm{e}^{\mathrm{i} m \theta} \end{equation}
\begin{equation} A^{(i)}(\theta)=\sum_{m=-\infty}^{\infty}a_{m,0}^{(i)}\ \mathrm{e}^{\mathrm{i} m \theta} \end{equation}
is the ![]() $\theta$-dependent far-field radiation coefficient due to the oscillation of the cylinder in the
$\theta$-dependent far-field radiation coefficient due to the oscillation of the cylinder in the ![]() $i$th mode.
$i$th mode.
3.4. Haskind relation
Some important relations in which the wave excitation forces and wave radiation damping can be calculated in terms of far-field radiation coefficients indirectly are derived in this section. A general mathematical preparation for further studies in the following subsections is given in Appendix A.
3.4.1. Excitation forces: HR
Using (A11), we may rewrite expression (3.7) for the excitation force (![]() $j=0$) as
$j=0$) as
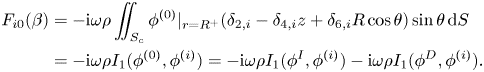 \begin{align} F_{i0}(\beta)&=-\mathrm{i} \omega \rho \iint_{S_c}\phi^{(0)}|_{r=R^+}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta) \sin \theta \,{\rm d} S\nonumber\\ &=-\mathrm{i} \omega \rho I_1(\phi^{(0)},\phi^{(i)})=-\mathrm{i} \omega \rho I_1(\phi^{I},\phi^{(i)})-\mathrm{i} \omega \rho I_1(\phi^{D},\phi^{(i)}). \end{align}
\begin{align} F_{i0}(\beta)&=-\mathrm{i} \omega \rho \iint_{S_c}\phi^{(0)}|_{r=R^+}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta) \sin \theta \,{\rm d} S\nonumber\\ &=-\mathrm{i} \omega \rho I_1(\phi^{(0)},\phi^{(i)})=-\mathrm{i} \omega \rho I_1(\phi^{I},\phi^{(i)})-\mathrm{i} \omega \rho I_1(\phi^{D},\phi^{(i)}). \end{align} Furthermore, because ![]() $\phi ^{D}$ and
$\phi ^{D}$ and ![]() $\phi ^{(i)}$ both satisfy the far-field radiation condition (see (2.9)), which means
$\phi ^{(i)}$ both satisfy the far-field radiation condition (see (2.9)), which means ![]() $I_1(\phi ^{D},\phi ^{(i)})=0$, we obtain
$I_1(\phi ^{D},\phi ^{(i)})=0$, we obtain
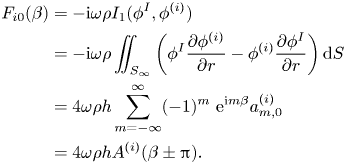 \begin{align} F_{i0}(\beta)&=-\mathrm{i} \omega \rho I_1(\phi^{I},\phi^{(i)})\nonumber\\ &=-\mathrm{i} \omega \rho\iint_{S_{\infty}}\left(\phi^{I}\frac{\partial \phi^{(i)}}{\partial r}-\phi^{(i)}\frac{\partial \phi^{I}}{\partial r}\right) {\rm d}S\nonumber\\ &=4\omega \rho h\sum_{m=-\infty}^{\infty}(-1)^m \ \mathrm{e}^{\mathrm{i} m \beta} a_{m,0}^{(i)}\nonumber\\ &=4\omega \rho h A^{(i)}(\beta\pm {\rm \pi}). \end{align}
\begin{align} F_{i0}(\beta)&=-\mathrm{i} \omega \rho I_1(\phi^{I},\phi^{(i)})\nonumber\\ &=-\mathrm{i} \omega \rho\iint_{S_{\infty}}\left(\phi^{I}\frac{\partial \phi^{(i)}}{\partial r}-\phi^{(i)}\frac{\partial \phi^{I}}{\partial r}\right) {\rm d}S\nonumber\\ &=4\omega \rho h\sum_{m=-\infty}^{\infty}(-1)^m \ \mathrm{e}^{\mathrm{i} m \beta} a_{m,0}^{(i)}\nonumber\\ &=4\omega \rho h A^{(i)}(\beta\pm {\rm \pi}). \end{align}It means that the excitation force the metamaterial cylinder experiences when a plane wave is incident from a certain direction is associated with the cylinder's ability to radiate a wave into just that direction. It enables the excitation forces to be expressed in terms of radiation parameters without any requirement of the solution of the wave scattering problem.
3.4.2. Reciprocity relation between radiation damping and excitation forces/far-field radiation coefficients
For the wave radiation forces (![]() $i,j \neq 0$), using (3.7) and (A11), and because
$i,j \neq 0$), using (3.7) and (A11), and because ![]() $\phi ^{(i)}$ and
$\phi ^{(i)}$ and ![]() $\phi ^{(\,j)}$ both satisfy the far-field radiation condition (see (2.9)), which means
$\phi ^{(\,j)}$ both satisfy the far-field radiation condition (see (2.9)), which means ![]() $I_1(\phi ^{(i)},\phi ^{(\,j)})=0$, we have
$I_1(\phi ^{(i)},\phi ^{(\,j)})=0$, we have
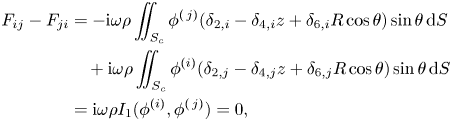 \begin{align} F_{ij}- F_{ji}&=-\mathrm{i} \omega \rho \iint_{S_c}\phi^{(\,j)}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta) \sin \theta \,{\rm d} S\nonumber\\ &\quad+\mathrm{i} \omega \rho \iint_{S_c}\phi^{(i)}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos\theta) \sin \theta \,{\rm d} S\nonumber\\ &=\mathrm{i} \omega \rho I_1(\phi^{(i)},\phi^{(\,j)})=0, \end{align}
\begin{align} F_{ij}- F_{ji}&=-\mathrm{i} \omega \rho \iint_{S_c}\phi^{(\,j)}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta) \sin \theta \,{\rm d} S\nonumber\\ &\quad+\mathrm{i} \omega \rho \iint_{S_c}\phi^{(i)}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos\theta) \sin \theta \,{\rm d} S\nonumber\\ &=\mathrm{i} \omega \rho I_1(\phi^{(i)},\phi^{(\,j)})=0, \end{align}
which proves the reciprocity relations ![]() $F_{ij}=F_{ji}$,
$F_{ij}=F_{ji}$, ![]() $c_{ij}=c_{ji}$ and
$c_{ij}=c_{ji}$ and ![]() $a_{ij}=a_{ji}$.
$a_{ij}=a_{ji}$.
Therefore, we have
 \begin{align} c_{ij}&=-\frac{1}{2} (F_{ij}+F_{ij}^*)=-\frac{1}{2} (F_{ij}+F_{ji}^*)\nonumber\\ &=\frac{\mathrm{i} \omega \rho}{2} \iint_{S_c}[\phi^{(\,j)}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta)- \phi^{(i)*}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos\theta)] \sin \theta \,{\rm d} S\nonumber\\ &=\frac{\mathrm{i} \omega \rho}{2}\left[I_1(\phi^{(\,j)},\phi^{(i)*})-\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2} \iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S\right]\nonumber\\ &=\omega \rho k\iint_{S_{\infty}} \phi^{(\,j)}\phi^{(i)*}\, {\rm d}S+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S\nonumber\\ &=4\omega \rho h\sum_{m=-\infty}^{\infty} a_{m,0}^{(\,j)}a_{m,0}^{(i)*}{+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S}\nonumber\\ &=\frac{1}{8{\rm \pi} \omega \rho h} \int_{0}^{2{\rm \pi}}F_{j0}(\beta)F_{i0}^*(\beta)\,{\rm d}\beta+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S\nonumber\\ &=\frac{2 \omega \rho h}{\rm \pi} \int_{0}^{2{\rm \pi}}A^{(\,j)}(\theta)A^{(i)*}(\theta)\,{\rm d}\theta+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S, \end{align}
\begin{align} c_{ij}&=-\frac{1}{2} (F_{ij}+F_{ij}^*)=-\frac{1}{2} (F_{ij}+F_{ji}^*)\nonumber\\ &=\frac{\mathrm{i} \omega \rho}{2} \iint_{S_c}[\phi^{(\,j)}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos\theta)- \phi^{(i)*}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos\theta)] \sin \theta \,{\rm d} S\nonumber\\ &=\frac{\mathrm{i} \omega \rho}{2}\left[I_1(\phi^{(\,j)},\phi^{(i)*})-\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2} \iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S\right]\nonumber\\ &=\omega \rho k\iint_{S_{\infty}} \phi^{(\,j)}\phi^{(i)*}\, {\rm d}S+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S\nonumber\\ &=4\omega \rho h\sum_{m=-\infty}^{\infty} a_{m,0}^{(\,j)}a_{m,0}^{(i)*}{+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S}\nonumber\\ &=\frac{1}{8{\rm \pi} \omega \rho h} \int_{0}^{2{\rm \pi}}F_{j0}(\beta)F_{i0}^*(\beta)\,{\rm d}\beta+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S\nonumber\\ &=\frac{2 \omega \rho h}{\rm \pi} \int_{0}^{2{\rm \pi}}A^{(\,j)}(\theta)A^{(i)*}(\theta)\,{\rm d}\theta+\frac{K\omega \rho \bar{v}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(\,j)}\phi^{(i)*}\, {\rm d}S, \end{align}indicating the relationship between the radiation damping and the far-field radiation coefficients/wave excitation forces.
The Haskind-type identities as given in (3.11) and (3.13) link up the wave scattering and radiation problems, and present a way to examine the accuracy of the proposed model.
3.5. Wave power dissipation
The wave power dissipated by the metamaterial cylinder in a stationary condition due to the damping mechanism can be calculated in a straightforward way,
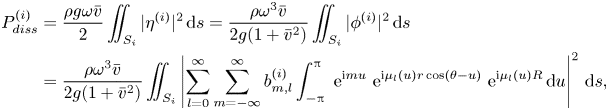 \begin{align} P_{diss}^{(i)}&=\frac{\rho g \omega \bar{v}}{2}\iint_{S_i} |\eta^{(i)}|^2\,{\rm d}s=\frac{\rho \omega^3 \bar{v}}{2 g (1+\bar{v}^2)}\iint_{S_i} |\phi^{(i)}|^2\,{\rm d}s\nonumber\\ &=\frac{\rho \omega^3 \bar{v}}{2 g (1+\bar{v}^2)}\iint_{S_i} \left|\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(i)} \int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}\,{\rm d}u \right|^2\,{\rm d}s, \end{align}
\begin{align} P_{diss}^{(i)}&=\frac{\rho g \omega \bar{v}}{2}\iint_{S_i} |\eta^{(i)}|^2\,{\rm d}s=\frac{\rho \omega^3 \bar{v}}{2 g (1+\bar{v}^2)}\iint_{S_i} |\phi^{(i)}|^2\,{\rm d}s\nonumber\\ &=\frac{\rho \omega^3 \bar{v}}{2 g (1+\bar{v}^2)}\iint_{S_i} \left|\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}b_{m,l}^{(i)} \int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}\,{\rm d}u \right|^2\,{\rm d}s, \end{align}
with ![]() $i=0$, which is called the ‘direct method’ hereinafter, where
$i=0$, which is called the ‘direct method’ hereinafter, where ![]() $S_i$ represents the free surface inside the cylinder. For the metamaterial cylinder forced to oscillate in still water in the
$S_i$ represents the free surface inside the cylinder. For the metamaterial cylinder forced to oscillate in still water in the ![]() $i$th mode with angular frequency
$i$th mode with angular frequency ![]() $\omega$ and amplitude
$\omega$ and amplitude ![]() $X_i$ (
$X_i$ (![]() $i = 2$, 4, 6), the wave power dissipated by the cylinder due to the damping mechanism can also be evaluated with the ‘direct method’, i.e. (3.14) but with a gain factor
$i = 2$, 4, 6), the wave power dissipated by the cylinder due to the damping mechanism can also be evaluated with the ‘direct method’, i.e. (3.14) but with a gain factor ![]() $\omega ^2|X_i|^2$ added to the right-hand side.
$\omega ^2|X_i|^2$ added to the right-hand side.
An alternative method is to use the energy conservation principle and express wave power dissipation indirectly in terms of the far-field coefficients ![]() $a_{m,0}^{(0)}$. More specifically, the wave power dissipated by a fixed metamaterial cylinder subjected to regular waves can be expressed as the difference between the incoming wave power coming towards the cylinder and the outgoing wave power propagating away from the cylinder (e.g. see Zheng et al. Reference Zheng, Michele, Liang, Meylan and Greaves2022a); whereas for the wave radiation problem, it could be expressed as the difference between the input power and the wave power radiated away from the cylinder due to its oscillation, i.e.
$a_{m,0}^{(0)}$. More specifically, the wave power dissipated by a fixed metamaterial cylinder subjected to regular waves can be expressed as the difference between the incoming wave power coming towards the cylinder and the outgoing wave power propagating away from the cylinder (e.g. see Zheng et al. Reference Zheng, Michele, Liang, Meylan and Greaves2022a); whereas for the wave radiation problem, it could be expressed as the difference between the input power and the wave power radiated away from the cylinder due to its oscillation, i.e.
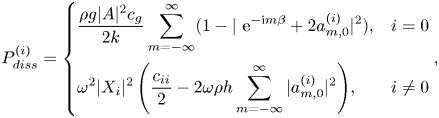 \begin{equation} P_{diss}^{(i)}=\begin{cases} \displaystyle \frac{\rho g |A|^2 c_g}{2k}\sum_{m=-\infty}^{\infty}(1-|\ \mathrm{e}^{-\mathrm{i} m \beta}+2 a_{m,0}^{(i)}|^2), & i=0\\ \displaystyle \omega^2 |X_i|^2 \left(\frac{c_{ii}}{2}-2\omega \rho h \sum_{m=-\infty}^{\infty}|a_{m,0}^{(i)}|^2\right)\!, & i\neq 0 \end{cases}, \end{equation}
\begin{equation} P_{diss}^{(i)}=\begin{cases} \displaystyle \frac{\rho g |A|^2 c_g}{2k}\sum_{m=-\infty}^{\infty}(1-|\ \mathrm{e}^{-\mathrm{i} m \beta}+2 a_{m,0}^{(i)}|^2), & i=0\\ \displaystyle \omega^2 |X_i|^2 \left(\frac{c_{ii}}{2}-2\omega \rho h \sum_{m=-\infty}^{\infty}|a_{m,0}^{(i)}|^2\right)\!, & i\neq 0 \end{cases}, \end{equation}
which, hereinafter, is called the ‘indirect method’, where ![]() $c_g$ denotes the wave group velocity
$c_g$ denotes the wave group velocity ![]() $c_g={\omega }/[{2k}(1+{2kh}/{\sinh (2kh)})]$.
$c_g={\omega }/[{2k}(1+{2kh}/{\sinh (2kh)})]$.
The comparison between the predicted wave power dissipation by using the direct and indirect methods provides an approach to check the accuracy of the proposed model.
It should be pointed out that the wave power dissipation discussed above is for separate wave scattering and wave radiation problems. For the oscillating metamaterial cylinder excited by incident waves, the overall wave power dissipated due to the damping mechanism may be calculated by using the direct and indirect methods
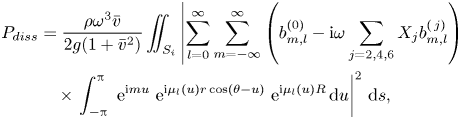 \begin{align} P_{diss}&=\frac{\rho \omega^3 \bar{v}}{2 g (1+\bar{v}^2)}\iint_{S_i} \left|\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}\left(b_{m,l}^{(0)}-\mathrm{i}\omega \sum_{j=2,4,6}X_jb_{m,l}^{(\,j)}\right)\right.\nonumber\\ &\quad \times \left.\int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}\,{\rm d}u \right|^2\,{\rm d}s, \end{align}
\begin{align} P_{diss}&=\frac{\rho \omega^3 \bar{v}}{2 g (1+\bar{v}^2)}\iint_{S_i} \left|\sum_{l=0}^{\infty}\sum_{m=-\infty}^{\infty}\left(b_{m,l}^{(0)}-\mathrm{i}\omega \sum_{j=2,4,6}X_jb_{m,l}^{(\,j)}\right)\right.\nonumber\\ &\quad \times \left.\int_{-{\rm \pi}}^{\rm \pi}\ \mathrm{e}^{\mathrm{i} m u}\ \mathrm{e}^{\mathrm{i} \mu_l(u)r\cos(\theta-u)}\ \mathrm{e}^{\mathrm{i} \mu_l(u)R}\,{\rm d}u \right|^2\,{\rm d}s, \end{align}and
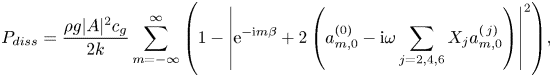 \begin{equation} P_{diss}= \frac{\rho g |A|^2 c_g}{2k}\sum_{m=-\infty}^{\infty}\left(1-\left|\mathrm{e}^{-\mathrm{i} m \beta}+2 \left(a_{m,0}^{(0)}-\mathrm{i}\omega \sum_{j=2,4,6}X_ja_{m,0}^{(\,j)}\right)\right|^2\right)\!, \end{equation}
\begin{equation} P_{diss}= \frac{\rho g |A|^2 c_g}{2k}\sum_{m=-\infty}^{\infty}\left(1-\left|\mathrm{e}^{-\mathrm{i} m \beta}+2 \left(a_{m,0}^{(0)}-\mathrm{i}\omega \sum_{j=2,4,6}X_ja_{m,0}^{(\,j)}\right)\right|^2\right)\!, \end{equation}respectively.
4. Model validation
Hereinafter, the wave excitation forces, hydrodynamic coefficients and the wave power dissipated by the metamaterial cylinder when stationary are presented in terms of dimensionless parameters defined as follows:
where ![]() $m=2$ for
$m=2$ for ![]() $i=2$, and
$i=2$, and ![]() $m=3$ for
$m=3$ for ![]() $i=4$ and 6;
$i=4$ and 6;
in which ![]() $m=3$ for
$m=3$ for ![]() $(i,j)=(2,2)$;
$(i,j)=(2,2)$; ![]() $m=4$ for
$m=4$ for ![]() $(i,j)=(2,4)$; and
$(i,j)=(2,4)$; and ![]() $m=5$ for
$m=5$ for ![]() $(i,j)=(4,4)$ and
$(i,j)=(4,4)$ and ![]() $(6,6)$;
$(6,6)$;
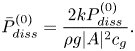 \begin{equation} \bar{P}_{diss}^{(0)}=\frac{2 k {P}_{diss}^{(0)}}{\rho g |A|^2 c_g}. \end{equation}
\begin{equation} \bar{P}_{diss}^{(0)}=\frac{2 k {P}_{diss}^{(0)}}{\rho g |A|^2 c_g}. \end{equation} A convergence analysis is carried out to examine the effect of the number of the truncated terms in terms of ![]() $M$ (
$M$ (![]() $m=-M, \ldots, M$) and
$m=-M, \ldots, M$) and ![]() $L$ (
$L$ (![]() $l=0, 1, \ldots, L$) on the frequency responses of the wave excitation forces, the results of which are given in Appendix B. In order to obtain the converged results,
$l=0, 1, \ldots, L$) on the frequency responses of the wave excitation forces, the results of which are given in Appendix B. In order to obtain the converged results, ![]() $M \ge 5$ and
$M \ge 5$ and ![]() $L \ge 4$ are suggested. Hereinafter,
$L \ge 4$ are suggested. Hereinafter, ![]() $M = 5$ and
$M = 5$ and ![]() $L = 4$ are adopted unless otherwise specified. The accuracy of the effective medium model developed in this paper is tested by comparing the present wave scattering results with those using the boundary element method of Liang et al. (Reference Liang, Zheng, Shao, Chua, Choo and Greaves2021) for an arrangement of 40 discrete thin vertical plates (see figure 2). Two wave conditions,
$L = 4$ are adopted unless otherwise specified. The accuracy of the effective medium model developed in this paper is tested by comparing the present wave scattering results with those using the boundary element method of Liang et al. (Reference Liang, Zheng, Shao, Chua, Choo and Greaves2021) for an arrangement of 40 discrete thin vertical plates (see figure 2). Two wave conditions, ![]() $kR=1.0$ and 1.3, are used here as an example for illustration of wave pattern in figure 2 for a cylinder extending through 20 % of the depth with
$kR=1.0$ and 1.3, are used here as an example for illustration of wave pattern in figure 2 for a cylinder extending through 20 % of the depth with ![]() $\bar {v}=0$. It indicates visibly satisfactory agreement between the present theoretical results and the numerical ones. The numerical results plotted in figures 2(b) and 2(d) are determined by using
$\bar {v}=0$. It indicates visibly satisfactory agreement between the present theoretical results and the numerical ones. The numerical results plotted in figures 2(b) and 2(d) are determined by using ![]() $7584$ quadrilateral panels, and there are
$7584$ quadrilateral panels, and there are ![]() $201\times 201=40\ 401$ points on the free surface. Because of the dense matrix in the boundary element method, the computation is very time consuming and storage intensive, and it takes approximately 16 min on a workstation for each wave condition. Whereas for the analytical model, it takes only approximately 1.7 min on a personal computer, showing the advantage of the low computational cost of the analytical model. The frequency responses of wave excitation forces acting on the vertical metamaterial cylinder by using analytical and numerical models are compared in figure 3. The mild differences between the effective medium results and the discrete computation as shown in figures 2 and 3 could be further reduced by increasing the number of plates in the numerical simulation provided more simulation time is acceptable.
$201\times 201=40\ 401$ points on the free surface. Because of the dense matrix in the boundary element method, the computation is very time consuming and storage intensive, and it takes approximately 16 min on a workstation for each wave condition. Whereas for the analytical model, it takes only approximately 1.7 min on a personal computer, showing the advantage of the low computational cost of the analytical model. The frequency responses of wave excitation forces acting on the vertical metamaterial cylinder by using analytical and numerical models are compared in figure 3. The mild differences between the effective medium results and the discrete computation as shown in figures 2 and 3 could be further reduced by increasing the number of plates in the numerical simulation provided more simulation time is acceptable.
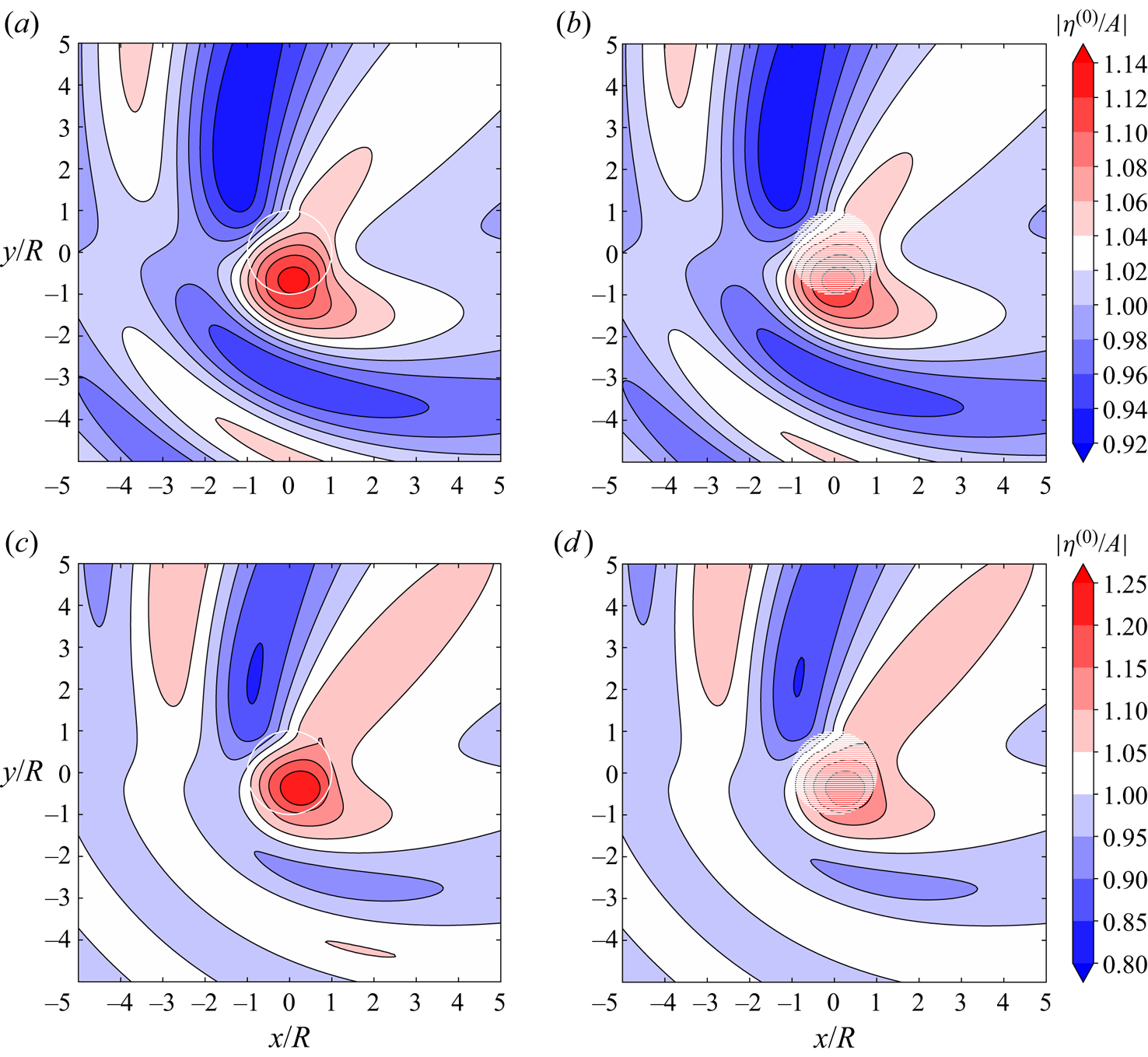
Figure 2. Wave motion due to incident wave propagation with ![]() $\beta ={\rm \pi} /4$ on a stationary truncated metamaterial cylinder with
$\beta ={\rm \pi} /4$ on a stationary truncated metamaterial cylinder with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.2$ and
$d/h=0.2$ and ![]() $\bar {v}=0$: (a,b)
$\bar {v}=0$: (a,b) ![]() $kR=1.0$; (c,d)
$kR=1.0$; (c,d) ![]() $kR=1.3$. Panels (a) and (c) are analytical results; (b) and (d) numerical results (Liang et al. Reference Liang, Zheng, Shao, Chua, Choo and Greaves2021), in which the cylinder was modelled by 40 infinitely thin vertical plates (see the horizontal lines on the cylinder). Here
$kR=1.3$. Panels (a) and (c) are analytical results; (b) and (d) numerical results (Liang et al. Reference Liang, Zheng, Shao, Chua, Choo and Greaves2021), in which the cylinder was modelled by 40 infinitely thin vertical plates (see the horizontal lines on the cylinder). Here ![]() $\eta ^{(0)}$ denotes the free surface elevation of the wave scattering problem.
$\eta ^{(0)}$ denotes the free surface elevation of the wave scattering problem.
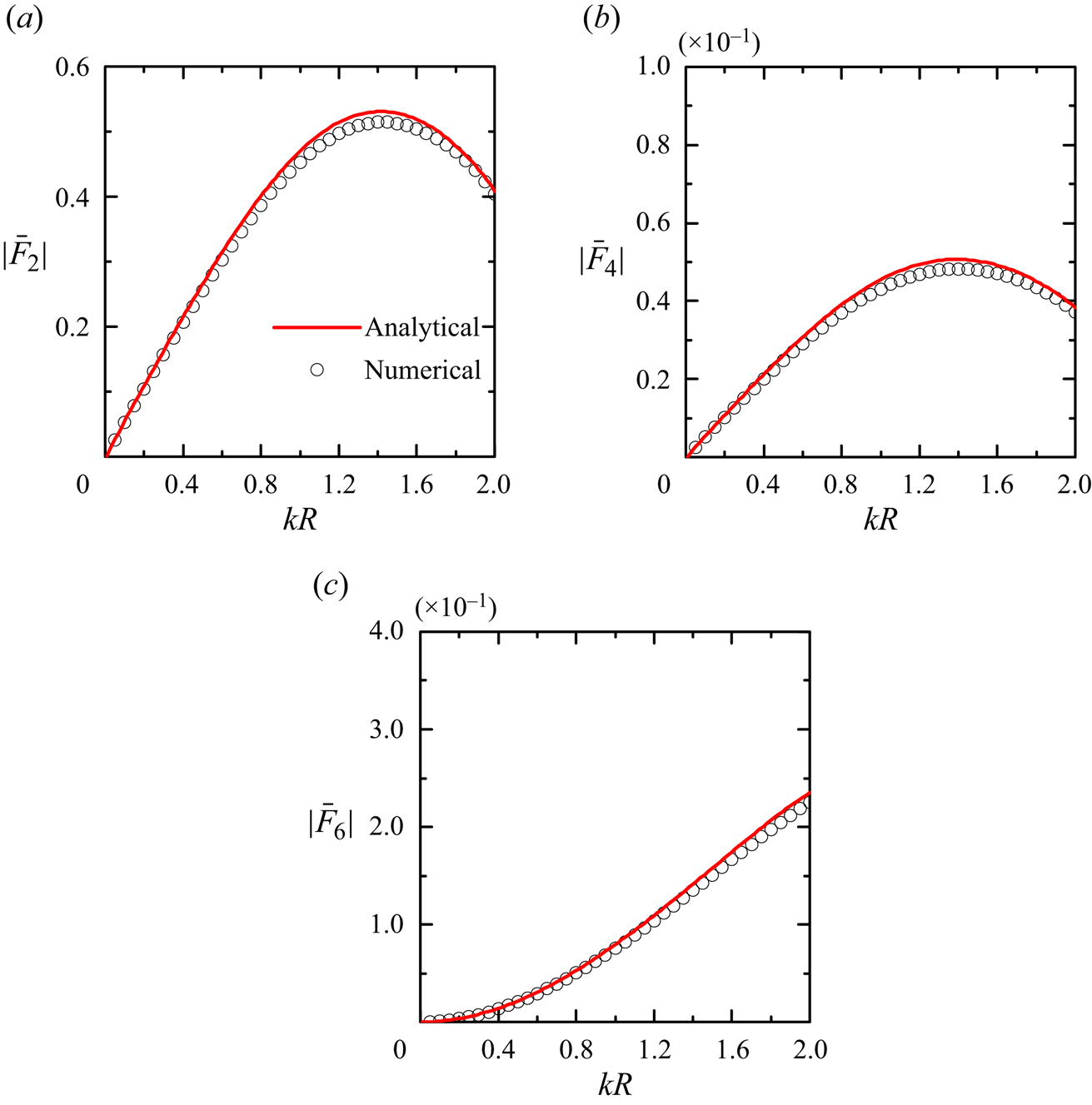
Figure 3. Frequency response of wave excitation forces experienced by a vertical truncated metamaterial cylinder with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.2$,
$d/h=0.2$, ![]() $\bar {v}=0$ and
$\bar {v}=0$ and ![]() $\beta ={\rm \pi} /4$: (a)
$\beta ={\rm \pi} /4$: (a) ![]() $|\bar {F}_2|$; (b)
$|\bar {F}_2|$; (b) ![]() $|\bar {F}_4|$ and (c)
$|\bar {F}_4|$ and (c) ![]() $|\bar {F}_6|$. Here ‘analytical’ denotes the present effective medium results and ‘numerical’ represents the discrete computation results, in which the cylinder was modelled by 40 infinitely thin vertical plates (Liang et al. Reference Liang, Zheng, Shao, Chua, Choo and Greaves2021).
$|\bar {F}_6|$. Here ‘analytical’ denotes the present effective medium results and ‘numerical’ represents the discrete computation results, in which the cylinder was modelled by 40 infinitely thin vertical plates (Liang et al. Reference Liang, Zheng, Shao, Chua, Choo and Greaves2021).
In addition to the wave field and wave excitation forces, we have also compared the dissipated wave power and the wave radiation damping coefficients with the employment of different methods in figure 4. It is noted that the damping parameter ![]() $\bar {v}$ cannot be determined within the potential flow theory in a straightforward manner, and instead it should be quantified via the experiments or solving the Navier–Stokes equations. Moreover, the roughness of the plate surface is sensitive to the damping coefficient
$\bar {v}$ cannot be determined within the potential flow theory in a straightforward manner, and instead it should be quantified via the experiments or solving the Navier–Stokes equations. Moreover, the roughness of the plate surface is sensitive to the damping coefficient ![]() $\bar {v}$. Therefore, for illustrative purposes, we consider a wide range of damping coefficients
$\bar {v}$. Therefore, for illustrative purposes, we consider a wide range of damping coefficients ![]() $\bar {v}\in [0.0,2.0]$. In figure 4, an excellent agreement between the results using different methods of wave excitation forces and hydrodynamic coefficients with the employment of different methods is obtained, indicating the accuracy of the present model in solving separate wave scattering and radiation problems.
$\bar {v}\in [0.0,2.0]$. In figure 4, an excellent agreement between the results using different methods of wave excitation forces and hydrodynamic coefficients with the employment of different methods is obtained, indicating the accuracy of the present model in solving separate wave scattering and radiation problems.
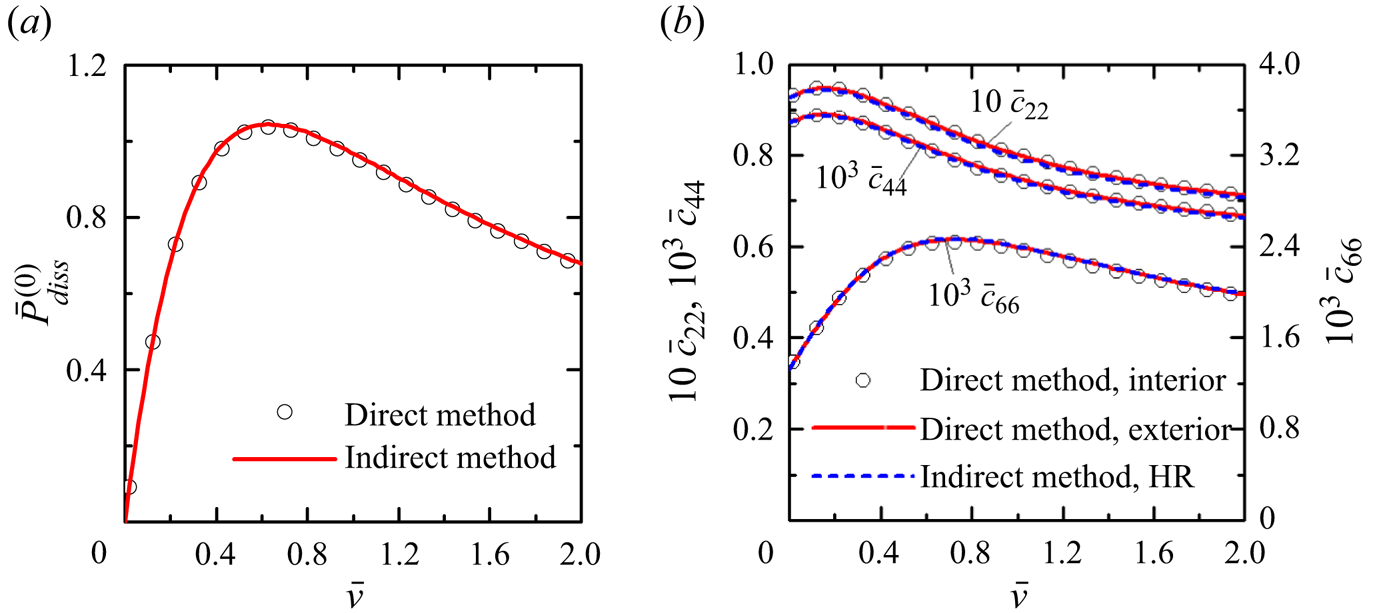
Figure 4. Variation of the non-dimensional wave power dissipation and wave radiation damping coefficients predicted by using different methods with respect to the damping parameter ![]() $\bar {v}$ for
$\bar {v}$ for ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.2$ and
$d/h=0.2$ and ![]() $kR=1.0$: (a)
$kR=1.0$: (a) ![]() $\bar {P}_{diss}^{(0)}$ with
$\bar {P}_{diss}^{(0)}$ with ![]() $\beta ={\rm \pi} /4$; (b)
$\beta ={\rm \pi} /4$; (b) ![]() $\bar {c}_{22}$,
$\bar {c}_{22}$, ![]() $\bar {c}_{44}$ and
$\bar {c}_{44}$ and ![]() $\bar {c}_{66}$. Here ‘direct method’ denotes the results by using (3.14), and ‘indirect method’ denotes the results by using (3.15); ‘direct method, interior’ denotes the results by using (3.4), ‘direct method, exterior’ denotes the results by using (3.7) and ‘indirect method, HR’ denotes the results by using (3.13), the HR.
$\bar {c}_{66}$. Here ‘direct method’ denotes the results by using (3.14), and ‘indirect method’ denotes the results by using (3.15); ‘direct method, interior’ denotes the results by using (3.4), ‘direct method, exterior’ denotes the results by using (3.7) and ‘indirect method, HR’ denotes the results by using (3.13), the HR.
5. Results and discussion
The validated model is applied to a series of case studies.
5.1. A truncated metamaterial cylinder without damping mechanism
Figure 5 illustrates the effect of the cylinder draft ![]() $d/h$ on the magnitude of the dimensionless wave excitation forces on a truncated metamaterial cylinder with
$d/h$ on the magnitude of the dimensionless wave excitation forces on a truncated metamaterial cylinder with ![]() $R/h=1.0$ subjected to incident regular waves of heading angle
$R/h=1.0$ subjected to incident regular waves of heading angle ![]() $\beta ={\rm \pi} /4$. The corresponding results of an equivalent solid cylinder of the same size are also plotted as controls. We note that in long waves, e.g.
$\beta ={\rm \pi} /4$. The corresponding results of an equivalent solid cylinder of the same size are also plotted as controls. We note that in long waves, e.g. ![]() $kR<0.5$, there is a linear interrelationship between
$kR<0.5$, there is a linear interrelationship between ![]() $|\bar {F}_2|$ and
$|\bar {F}_2|$ and ![]() $d/h$ (figure 5a), which is as expected because the excitation force is dominated by the Froude–Krylov force due to incident waves. Indeed, for
$d/h$ (figure 5a), which is as expected because the excitation force is dominated by the Froude–Krylov force due to incident waves. Indeed, for ![]() $kR<0.5$, the sway excitation forces acting on the truncated metamaterial cylinder and the equivalent solid cylinder of the same size are found to have a good qualitative agreement. As
$kR<0.5$, the sway excitation forces acting on the truncated metamaterial cylinder and the equivalent solid cylinder of the same size are found to have a good qualitative agreement. As ![]() $kR$ gets larger, the
$kR$ gets larger, the ![]() $|\bar {F}_2|-{kR}$ curves for the metamaterial cylinder deviate from those of the equivalent solid cylinder, and the deviation is generally upwards in the computed range of
$|\bar {F}_2|-{kR}$ curves for the metamaterial cylinder deviate from those of the equivalent solid cylinder, and the deviation is generally upwards in the computed range of ![]() $kR$, except around
$kR$, except around ![]() $kR=1.8$ for
$kR=1.8$ for ![]() $d/h=0.3\sim 0.5$, where an apparent downwards deviation occurs. This may be due to the wave near-trapping by the metamaterial cylinder, which will be discussed later in this paper.
$d/h=0.3\sim 0.5$, where an apparent downwards deviation occurs. This may be due to the wave near-trapping by the metamaterial cylinder, which will be discussed later in this paper.
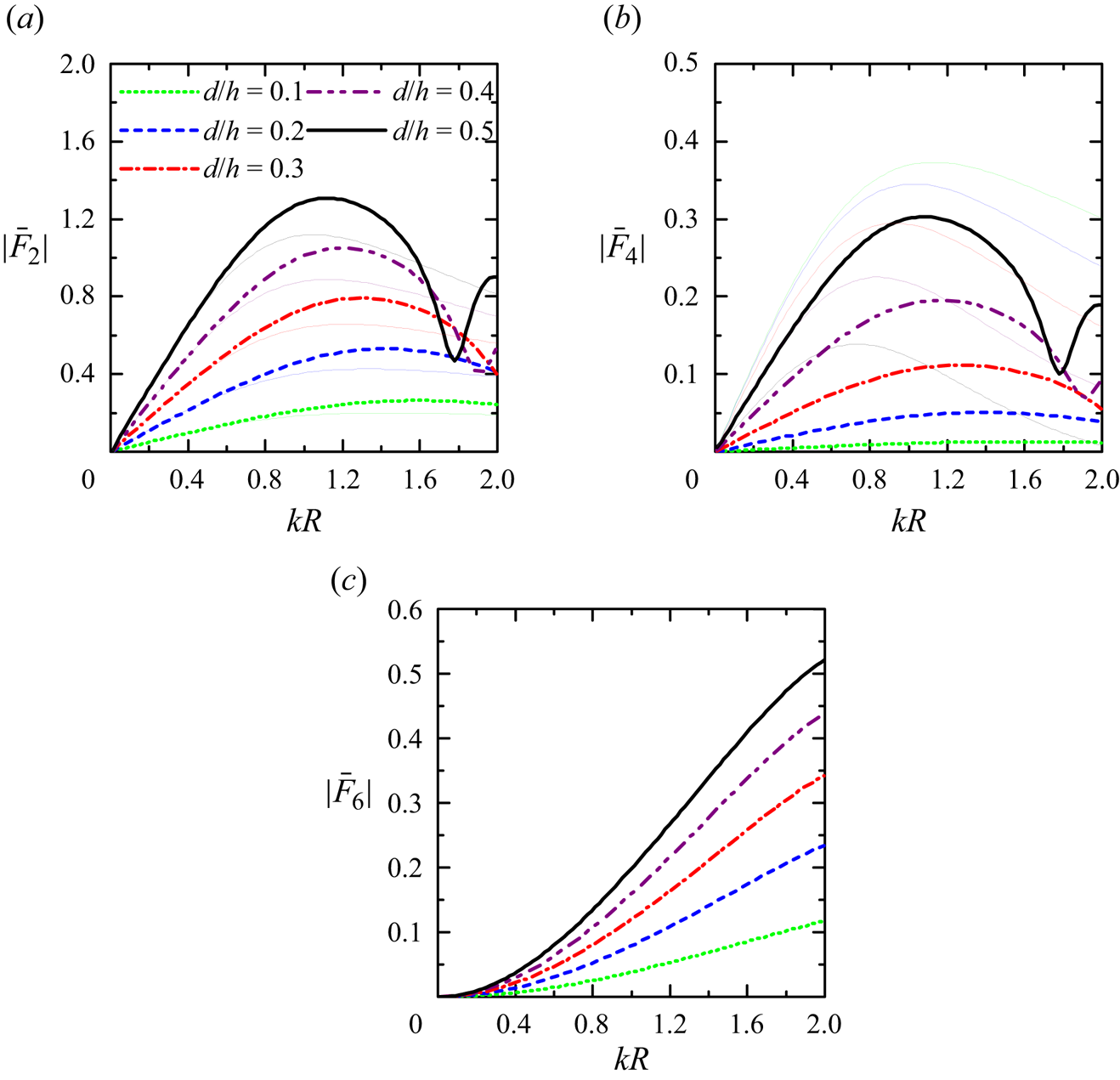
Figure 5. Frequency response of wave excitation forces experienced by a vertical truncated metamaterial cylinder (thick curves) with ![]() $R/h=1.0$ and
$R/h=1.0$ and ![]() $\beta ={\rm \pi} /4$: (a)
$\beta ={\rm \pi} /4$: (a) ![]() $|\bar {F}_2|$; (b)
$|\bar {F}_2|$; (b) ![]() $|\bar {F}_4|$; (c)
$|\bar {F}_4|$; (c) ![]() $|\bar {F}_6|$. The corresponding wave excitation forces experienced by an equivalent solid cylinder of the same size are also plotted as a comparison (see the solid thin curves). The curves in the same colour denote the results with the same value of
$|\bar {F}_6|$. The corresponding wave excitation forces experienced by an equivalent solid cylinder of the same size are also plotted as a comparison (see the solid thin curves). The curves in the same colour denote the results with the same value of ![]() $d/h$.
$d/h$.
For the metamaterial cylinder, the shapes of the ![]() $|\bar {F}_4|-kR$ curves (figure 5b) are observed to be similar to those of the
$|\bar {F}_4|-kR$ curves (figure 5b) are observed to be similar to those of the ![]() $|\bar {F}_2|-kR$ curves. Nevertheless, for the equivalent solid cylinder, the
$|\bar {F}_2|-kR$ curves. Nevertheless, for the equivalent solid cylinder, the ![]() $|\bar {F}_4|-{kR}$ curves perform rather differently from the corresponding
$|\bar {F}_4|-{kR}$ curves perform rather differently from the corresponding ![]() $|\bar {F}_2|-{kR}$ curves. This is because the roll excitation force acting on a solid truncated cylinder is influenced not only by the hydrodynamic pressure acting on the curved sidewall but also by that acting on the bottom of the cylinder. In most of the computed range of
$|\bar {F}_2|-{kR}$ curves. This is because the roll excitation force acting on a solid truncated cylinder is influenced not only by the hydrodynamic pressure acting on the curved sidewall but also by that acting on the bottom of the cylinder. In most of the computed range of ![]() ${kR}$, e.g.
${kR}$, e.g. ![]() $kR<1.6$, the larger
$kR<1.6$, the larger ![]() $d/h$, the larger
$d/h$, the larger ![]() $|\bar {F}_4|$ of the metamaterial cylinder. On the contrary, the value of
$|\bar {F}_4|$ of the metamaterial cylinder. On the contrary, the value of ![]() $|\bar {F}_4|$ for the equivalent solid cylinder decreases with increasing
$|\bar {F}_4|$ for the equivalent solid cylinder decreases with increasing ![]() $d/h$. This could be because the hydrodynamic pressure acting on the bottom of the solid cylinder dominates
$d/h$. This could be because the hydrodynamic pressure acting on the bottom of the solid cylinder dominates ![]() $|\bar {F}_4|$, and the hydrodynamics at a deeper position is less intensive than that at a shallower position.
$|\bar {F}_4|$, and the hydrodynamics at a deeper position is less intensive than that at a shallower position.
For a solid cylinder, there is no yaw wave excitation force. While due to the existence of the closely deployed vertical barriers, between which fluid motion occurs, the yaw wave excitation force acting on the metamaterial cylinder can be excited (figure 5c). In the examined range of wave conditions, ![]() $|\bar {F}_6|$ of the metamaterial cylinder presents a monotonic increase with the increase of
$|\bar {F}_6|$ of the metamaterial cylinder presents a monotonic increase with the increase of ![]() ${kR}$. For any specific
${kR}$. For any specific ![]() ${kR}$, the larger
${kR}$, the larger ![]() $d/h$, the larger
$d/h$, the larger ![]() $|\bar {F}_6|$.
$|\bar {F}_6|$.
The frequency responses of wave radiation damping and added mass of the metamaterial cylinder, as well as those of the equivalent solid cylinder of the same size, are plotted in figures 6 and 7, respectively. We observe that the curves of ![]() $\bar {c}_{22}$,
$\bar {c}_{22}$, ![]() $\bar {c}_{44}$ and
$\bar {c}_{44}$ and ![]() $\bar {c}_{66}$ with
$\bar {c}_{66}$ with ![]() $kR$ are qualitatively similar to those of
$kR$ are qualitatively similar to those of ![]() $|\bar {F}_2|$,
$|\bar {F}_2|$, ![]() $|\bar {F}_4|$ and
$|\bar {F}_4|$ and ![]() $|\bar {F}_6|$ in figure 5. Note, however, that the effect of
$|\bar {F}_6|$ in figure 5. Note, however, that the effect of ![]() $d/h$ on the wave radiation damping is more intense than that on wave excitation forces. A sharp valley of the curves
$d/h$ on the wave radiation damping is more intense than that on wave excitation forces. A sharp valley of the curves ![]() $\bar {c}_{22}$,
$\bar {c}_{22}$, ![]() $\bar {c}_{44}$ and
$\bar {c}_{44}$ and ![]() $\bar {c}_{24}$ is observed at
$\bar {c}_{24}$ is observed at ![]() $kR=1.8$ for the metamaterial cylinder with
$kR=1.8$ for the metamaterial cylinder with ![]() $d/h=0.5$. A similar feature also appears in the other cases, and the smaller
$d/h=0.5$. A similar feature also appears in the other cases, and the smaller ![]() $d/h$, the larger
$d/h$, the larger ![]() $kR$ where it occurs. In the range of computed
$kR$ where it occurs. In the range of computed ![]() $kR$ regardless of the value of
$kR$ regardless of the value of ![]() $d/h$,
$d/h$, ![]() $\bar {c}_{24}$ of the solid cylinder is negative and satisfies
$\bar {c}_{24}$ of the solid cylinder is negative and satisfies ![]() $\bar {c}_{24}^2=\bar {c}_{22}\bar {c}_{44}$, which can be derived by using the reciprocity relation between radiation damping and excitation force for 2-D symmetric bodies (Fernandes Reference Fernandes1989) and 3-D axisymmetric bodies (Falnes Reference Falnes2002). Here
$\bar {c}_{24}^2=\bar {c}_{22}\bar {c}_{44}$, which can be derived by using the reciprocity relation between radiation damping and excitation force for 2-D symmetric bodies (Fernandes Reference Fernandes1989) and 3-D axisymmetric bodies (Falnes Reference Falnes2002). Here ![]() $\bar {c}_{24}$ is positive or negative when the excitation forces for sway and roll are in the same phase or in opposite phases, respectively. Here
$\bar {c}_{24}$ is positive or negative when the excitation forces for sway and roll are in the same phase or in opposite phases, respectively. Here ![]() $\bar {c}_{24}^2=\bar {c}_{22}\bar {c}_{44}$ is also satisfied by the radiation damping coefficients of the metamaterial cylinder but with positive
$\bar {c}_{24}^2=\bar {c}_{22}\bar {c}_{44}$ is also satisfied by the radiation damping coefficients of the metamaterial cylinder but with positive ![]() $\bar {c}_{24}$ in the computed range of
$\bar {c}_{24}$ in the computed range of ![]() $kR$.
$kR$.
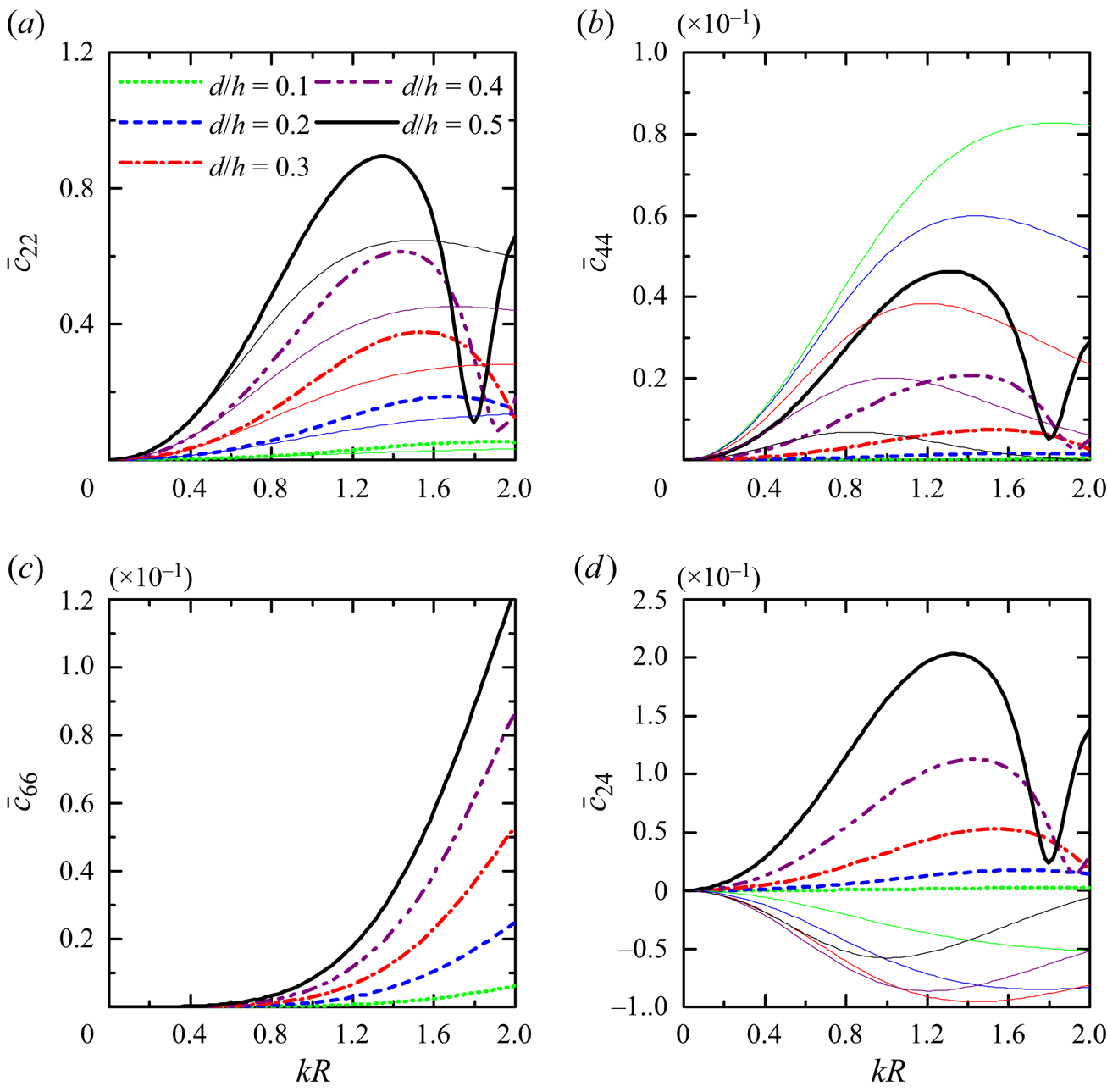
Figure 6. Frequency response of wave radiation damping of a vertical truncated metamaterial cylinder (thick curves) with ![]() $R/h=1.0$: (a)
$R/h=1.0$: (a) ![]() $\bar {c}_{22}$; (b)
$\bar {c}_{22}$; (b) ![]() $\bar {c}_{44}$; (c)
$\bar {c}_{44}$; (c) ![]() $\bar {c}_{66}$; (d)
$\bar {c}_{66}$; (d) ![]() $\bar {c}_{24}$. The corresponding wave radiation damping of an equivalent solid cylinder of the same size is also plotted as a comparison (see the solid thin curves). The curves in the same colour denote the results with the same value of
$\bar {c}_{24}$. The corresponding wave radiation damping of an equivalent solid cylinder of the same size is also plotted as a comparison (see the solid thin curves). The curves in the same colour denote the results with the same value of ![]() $d/h$.
$d/h$.
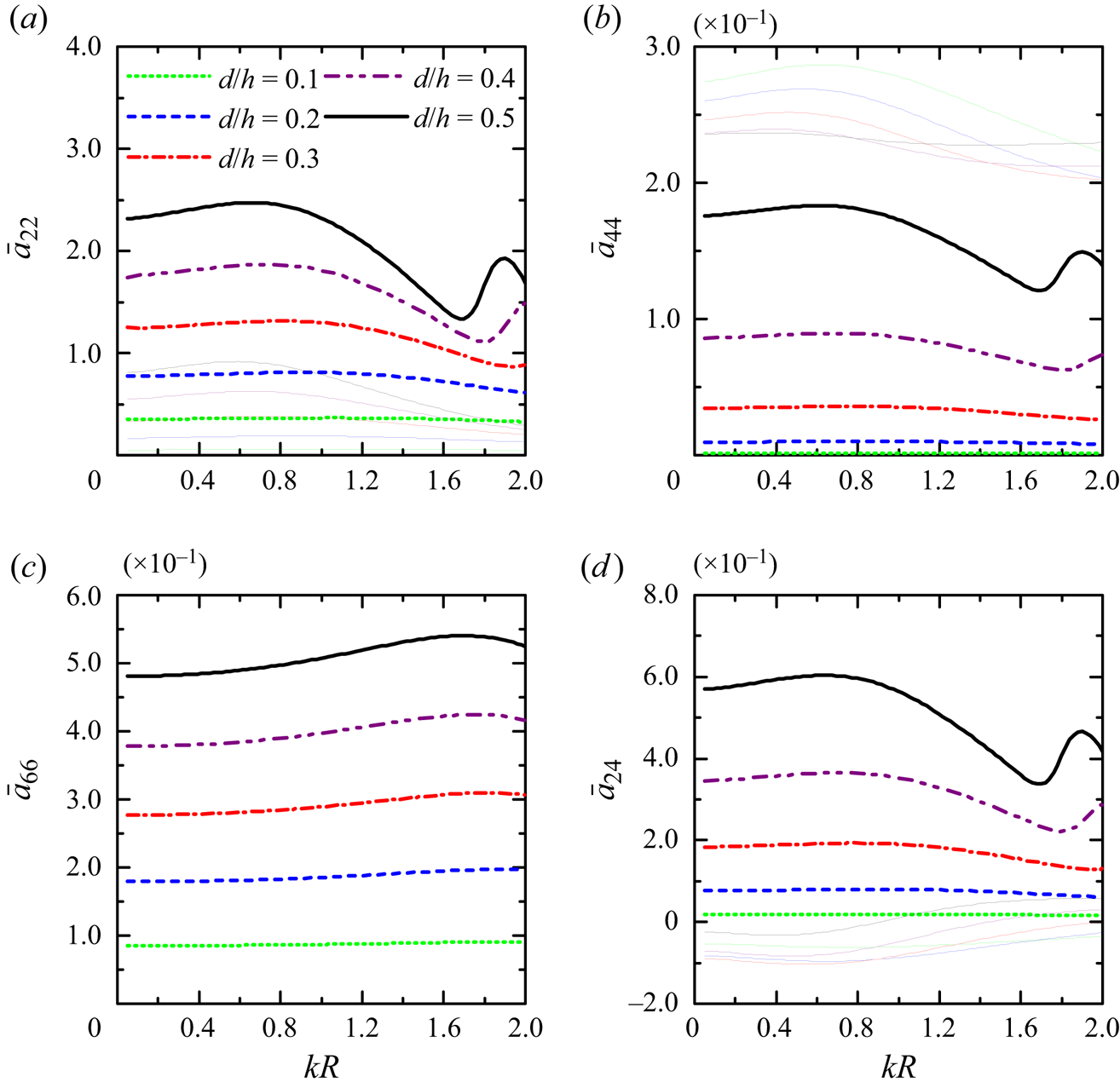
Figure 7. Frequency response of added mass of a vertical truncated metamaterial cylinder (thick curves) with ![]() $R/h=1.0$: (a)
$R/h=1.0$: (a) ![]() $\bar {a}_{22}$; (b)
$\bar {a}_{22}$; (b) ![]() $\bar {a}_{44}$; (c)
$\bar {a}_{44}$; (c) ![]() $\bar {a}_{66}$; (d)
$\bar {a}_{66}$; (d) ![]() $\bar {a}_{24}$. The corresponding added mass of an equivalent solid cylinder of the same size is also plotted as a comparison (see the solid thin curves). The curves in the same colour denote the results with the same value of
$\bar {a}_{24}$. The corresponding added mass of an equivalent solid cylinder of the same size is also plotted as a comparison (see the solid thin curves). The curves in the same colour denote the results with the same value of ![]() $d/h$.
$d/h$.
The added mass of the metamaterial cylinder as plotted in figure 7 is finite as ![]() $kR$ approaches zero, and the limiting values are different for the cases with different values of
$kR$ approaches zero, and the limiting values are different for the cases with different values of ![]() $d/h$: the larger
$d/h$: the larger ![]() $d/h$, the larger these limiting values. Here
$d/h$, the larger these limiting values. Here ![]() $\bar {a}_{22}$ of the metamaterial cylinder is generally larger than that of the equivalent solid cylinder. Figure 7(b) shows that
$\bar {a}_{22}$ of the metamaterial cylinder is generally larger than that of the equivalent solid cylinder. Figure 7(b) shows that ![]() $\bar {a}_{44}$ of the metamaterial cylinder is much smaller than that of the solid cylinder, and the difference, again, may be explained by the contribution of the hydrodynamics at the bottom of the cylinder. Interestingly,
$\bar {a}_{44}$ of the metamaterial cylinder is much smaller than that of the solid cylinder, and the difference, again, may be explained by the contribution of the hydrodynamics at the bottom of the cylinder. Interestingly, ![]() $\bar {a}_{22}$,
$\bar {a}_{22}$, ![]() $\bar {a}_{44}$ and
$\bar {a}_{44}$ and ![]() $\bar {a}_{24}$ of the metamaterial cylinder with
$\bar {a}_{24}$ of the metamaterial cylinder with ![]() $d/h=0.5$ exhibit an inverted ‘
$d/h=0.5$ exhibit an inverted ‘![]() $N$’ shaped curve at
$N$’ shaped curve at ![]() $kR=1.8$ corresponding to the sharp valley of the wave radiation damping curves. It means that at that particular frequency, standing waves are trapped in the region bounded by the cylinder whose energy slowly leaks away to infinity. We term this phenomenon ‘wave near-trapping’. The wave near-trapping frequency moves towards low frequencies as the draft of the truncated metamaterial cylinder increases.
$kR=1.8$ corresponding to the sharp valley of the wave radiation damping curves. It means that at that particular frequency, standing waves are trapped in the region bounded by the cylinder whose energy slowly leaks away to infinity. We term this phenomenon ‘wave near-trapping’. The wave near-trapping frequency moves towards low frequencies as the draft of the truncated metamaterial cylinder increases.
To have a better understanding of what is happening at ![]() ${kR}=1.8$, we plot the radiated wave field of a metamaterial cylinder with
${kR}=1.8$, we plot the radiated wave field of a metamaterial cylinder with ![]() $R/h=1.0$ and
$R/h=1.0$ and ![]() $d/h=0.5$ under swaying oscillations of unit velocity amplitude in figure 8, showing both wave amplitude and instantaneous free surface elevation non-dimensionalised by the sway motion amplitude
$d/h=0.5$ under swaying oscillations of unit velocity amplitude in figure 8, showing both wave amplitude and instantaneous free surface elevation non-dimensionalised by the sway motion amplitude ![]() $1/(-\mathrm {i} \omega )$. The radiated wave field for
$1/(-\mathrm {i} \omega )$. The radiated wave field for ![]() ${kR}=1.2$ is also plotted as a comparison. As shown in figures 8(a) and 8(c), the radiated wave field performs in a dipolar pattern for
${kR}=1.2$ is also plotted as a comparison. As shown in figures 8(a) and 8(c), the radiated wave field performs in a dipolar pattern for ![]() ${kR}=1.2$, and the sources are located at
${kR}=1.2$, and the sources are located at ![]() $\theta =\pm {\rm \pi}/2$ near the edge of the cylinder. This is roughly the same as that of an equivalent solid cylinder undergoing swaying motions (not plotted here). When the oscillating frequency reaches
$\theta =\pm {\rm \pi}/2$ near the edge of the cylinder. This is roughly the same as that of an equivalent solid cylinder undergoing swaying motions (not plotted here). When the oscillating frequency reaches ![]() ${kR}=1.8$, we observe from figures 8(b) and 8(d) that, in addition to the intense free surface response at
${kR}=1.8$, we observe from figures 8(b) and 8(d) that, in addition to the intense free surface response at ![]() $\theta =\pm {\rm \pi}/2$ near the circular edge, a larger wave motion is excited inside the metamaterial cylinder roughly at
$\theta =\pm {\rm \pi}/2$ near the circular edge, a larger wave motion is excited inside the metamaterial cylinder roughly at ![]() $r/R=0.4$,
$r/R=0.4$, ![]() $\theta =\pm {\rm \pi}/2$. Correspondingly, from the perspective of the exterior radiated wave field, two more dipoles are generated at the edge, one at
$\theta =\pm {\rm \pi}/2$. Correspondingly, from the perspective of the exterior radiated wave field, two more dipoles are generated at the edge, one at ![]() ${x/R}=-0.9$ with the two monopolar sources located at
${x/R}=-0.9$ with the two monopolar sources located at ![]() ${y/R}=\pm 0.4$, and the other at
${y/R}=\pm 0.4$, and the other at ![]() ${x/R}=0.9$ with the two monopolar sources located at
${x/R}=0.9$ with the two monopolar sources located at ![]() $y/R=\pm 0.4$. The two large wave motion-induced dipoles within the cylinder are roughly out of phase with those at the circular edge, partially offsetting one another at the far-field and resulting in a local valley of the wave radiation damping curves.
$y/R=\pm 0.4$. The two large wave motion-induced dipoles within the cylinder are roughly out of phase with those at the circular edge, partially offsetting one another at the far-field and resulting in a local valley of the wave radiation damping curves.
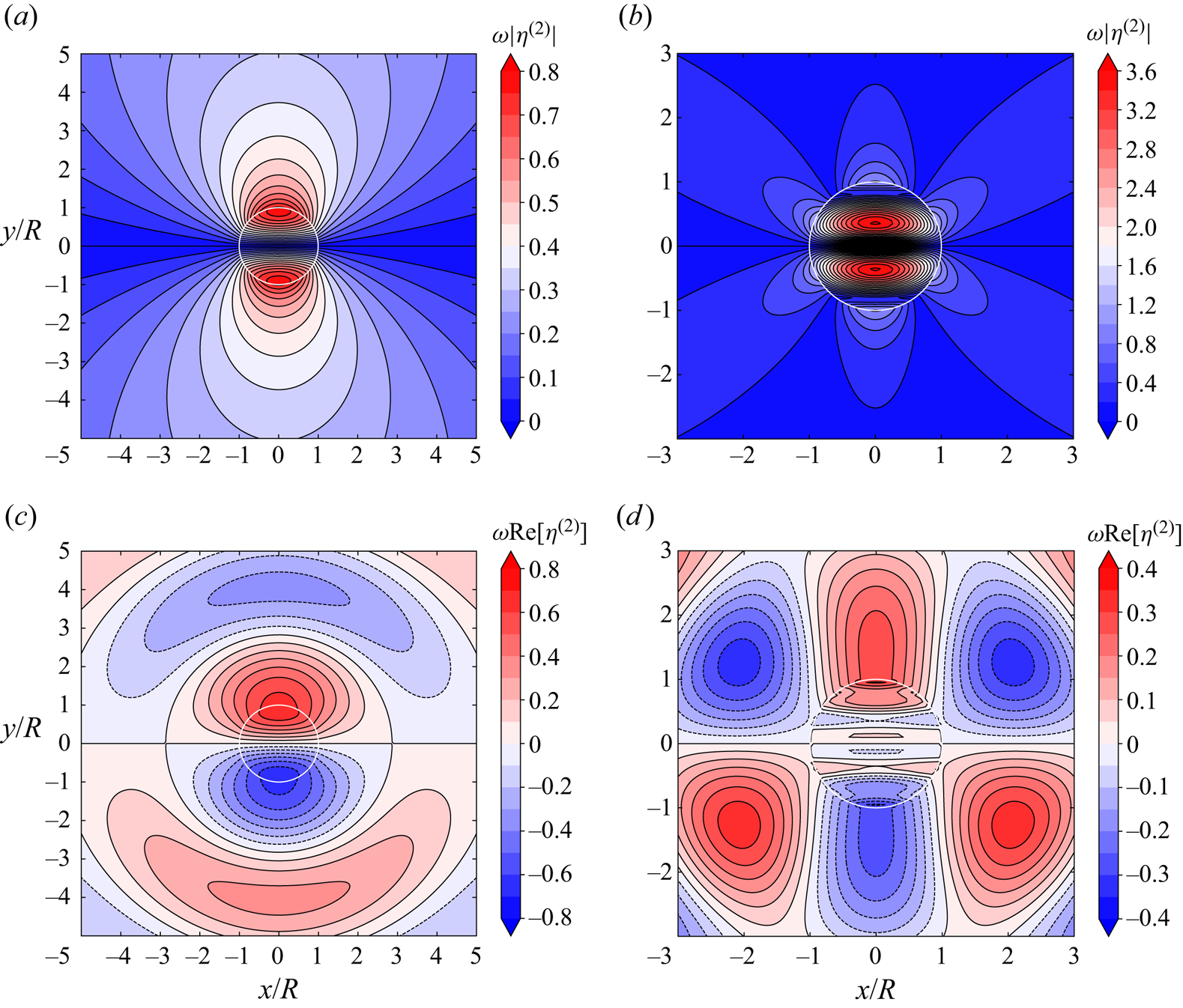
Figure 8. Sway-induced radiated wave field with ![]() $R/h=1.0$ and
$R/h=1.0$ and ![]() $d/h=0.5$: (a) and (b) amplitude field,
$d/h=0.5$: (a) and (b) amplitude field, ![]() $\omega |\eta ^{(2)}|$; (c) and (d) instantaneous wave field,
$\omega |\eta ^{(2)}|$; (c) and (d) instantaneous wave field, ![]() $\omega {\rm Re}[\eta ^{(2)}]$. Here (a) and (c)
$\omega {\rm Re}[\eta ^{(2)}]$. Here (a) and (c) ![]() $kR=1.2$; (b) and (d)
$kR=1.2$; (b) and (d) ![]() $kR=1.8$.
$kR=1.8$.
Returning to figures 6 and 7, we cannot see any sharp valley of ![]() $\bar {c}_{66}$ nor inverted ‘
$\bar {c}_{66}$ nor inverted ‘![]() $N$’ shaped
$N$’ shaped ![]() $\bar {a}_{66}$ curve. This is because the examined range of
$\bar {a}_{66}$ curve. This is because the examined range of ![]() $kR$ is not broad enough to cover the yaw motion-related wave near-trapping frequencies, which are generally larger than those of the sway and roll modes. Enlarging the radius of the metamaterial cylinder can effectively reduce the near-trapping frequency. Figure 9 presents the radiated wave field of metamaterial cylinders of different radii and
$kR$ is not broad enough to cover the yaw motion-related wave near-trapping frequencies, which are generally larger than those of the sway and roll modes. Enlarging the radius of the metamaterial cylinder can effectively reduce the near-trapping frequency. Figure 9 presents the radiated wave field of metamaterial cylinders of different radii and ![]() $d/h=0.5$ oscillating in yaw with
$d/h=0.5$ oscillating in yaw with ![]() ${kh}=1.66$. For the yaw wave radiation problem, the velocity potential may be decomposed as a series of circular components in terms of
${kh}=1.66$. For the yaw wave radiation problem, the velocity potential may be decomposed as a series of circular components in terms of ![]() $\sin (2m\theta )$ with
$\sin (2m\theta )$ with ![]() $m=1, 2, \ldots$. When the radius of the cylinder or the wave frequency is small, the circular components of the yaw-motion induced radiated wave field are dominated by the
$m=1, 2, \ldots$. When the radius of the cylinder or the wave frequency is small, the circular components of the yaw-motion induced radiated wave field are dominated by the ![]() $\sin (2\theta )$ component (figures 9a and 9c), and there are four sources of the radiated waves, which are located at
$\sin (2\theta )$ component (figures 9a and 9c), and there are four sources of the radiated waves, which are located at ![]() $\theta =\pm {\rm \pi}/4$ and
$\theta =\pm {\rm \pi}/4$ and ![]() $\pm 3{\rm \pi} /4$, respectively, on the edge of the cylinder. When the oscillating frequency or the radius of the cylinder is large enough, large-amplitude wave motion can be excited inside the metamaterial cylinder in yaw motion, and meanwhile the high-order circular component of the velocity potential outside the cylinder, e.g.
$\pm 3{\rm \pi} /4$, respectively, on the edge of the cylinder. When the oscillating frequency or the radius of the cylinder is large enough, large-amplitude wave motion can be excited inside the metamaterial cylinder in yaw motion, and meanwhile the high-order circular component of the velocity potential outside the cylinder, e.g. ![]() $\sin (4\theta )$ as shown in figures 9(b) and 9(d), is excited.
$\sin (4\theta )$ as shown in figures 9(b) and 9(d), is excited.
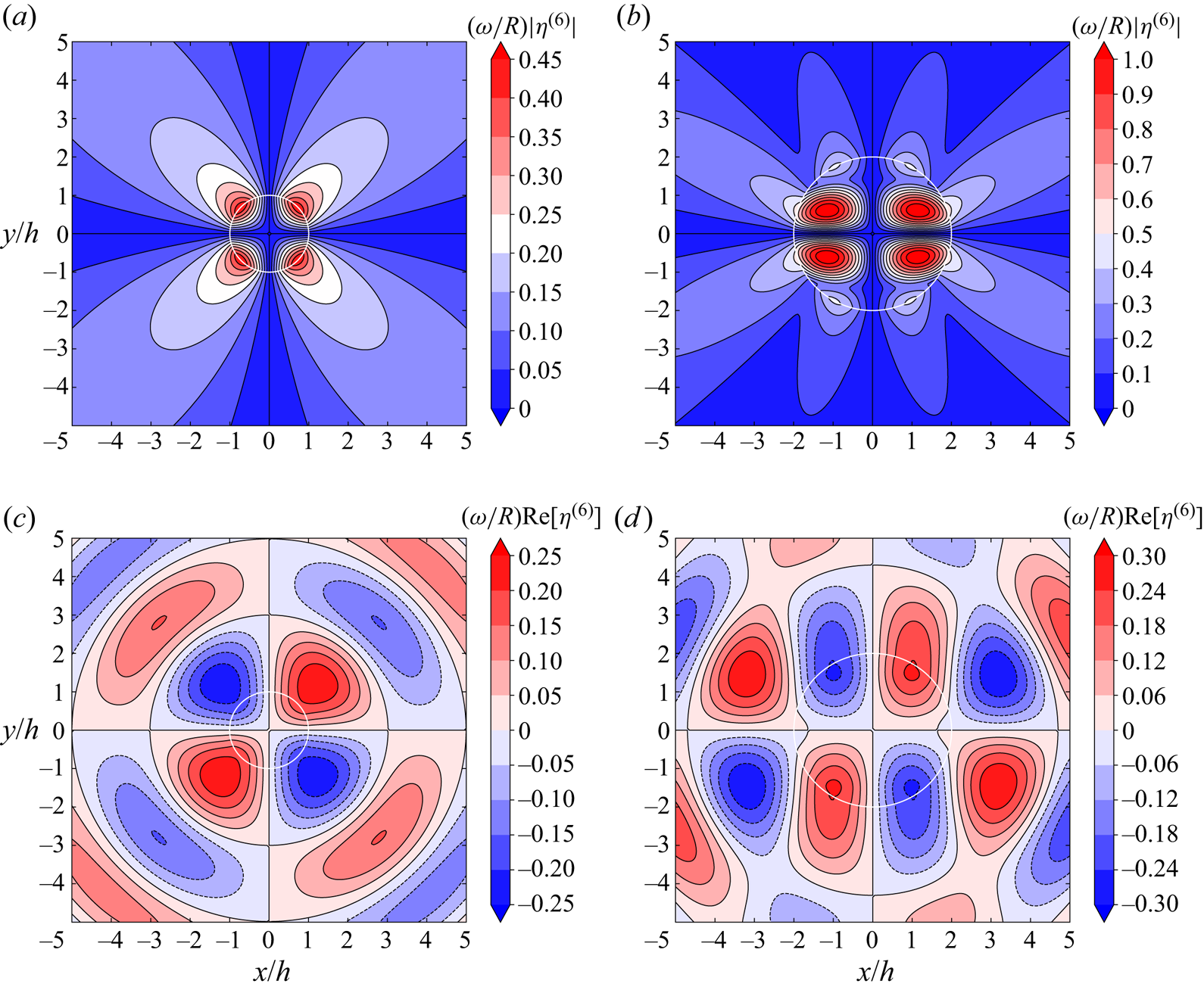
Figure 9. Yaw-induced radiated wave field with ![]() $d/h=0.5$ and
$d/h=0.5$ and ![]() $kh=1.66$: Here (a) and (b) amplitude field,
$kh=1.66$: Here (a) and (b) amplitude field, ![]() $\omega |\eta ^{(6)}|/R$; (c) and (d) instantaneous wave field,
$\omega |\eta ^{(6)}|/R$; (c) and (d) instantaneous wave field, ![]() $\omega {\rm Re}[\eta ^{(6)}]/R$. Here (a) and (c)
$\omega {\rm Re}[\eta ^{(6)}]/R$. Here (a) and (c) ![]() $R/h=1.0$; (b) and (d)
$R/h=1.0$; (b) and (d) ![]() $R/h=2.0$.
$R/h=2.0$.
5.2. A truncated metamaterial cylinder with damping mechanism
In this subsection, we take the truncated metamaterial cylinder with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.5$ and different values of
$d/h=0.5$ and different values of ![]() $\bar {v}$ as an example to demonstrate how a damping mechanism at the free surface inside the cylinder influences the wave scattering and radiation problems.
$\bar {v}$ as an example to demonstrate how a damping mechanism at the free surface inside the cylinder influences the wave scattering and radiation problems.
Figure 10 presents the frequency responses of wave excitation forces acting on the structured cylinder for ![]() $\bar {v}$ ranging between 0 and 0.8. For low wave frequencies, e.g.
$\bar {v}$ ranging between 0 and 0.8. For low wave frequencies, e.g. ![]() ${kR}<0.6$, the wave excitation forces are nearly independent of the change of
${kR}<0.6$, the wave excitation forces are nearly independent of the change of ![]() $\bar {v}$ in the examined range. This was to be expected because the damping parameter is embodied in
$\bar {v}$ in the examined range. This was to be expected because the damping parameter is embodied in ![]() $\mathcal {K}=K/(1-\bar {v}\ \mathrm{i})$ in the model (see (2.4)), meaning that when
$\mathcal {K}=K/(1-\bar {v}\ \mathrm{i})$ in the model (see (2.4)), meaning that when ![]() $K$ is small enough,
$K$ is small enough, ![]() $\mathcal {K}$ is insensitive to the change of
$\mathcal {K}$ is insensitive to the change of ![]() $\bar {v}$. For
$\bar {v}$. For ![]() $0.8<{kR}<1.6$, as
$0.8<{kR}<1.6$, as ![]() $\bar {v}$ increases from 0 to 0.8, both
$\bar {v}$ increases from 0 to 0.8, both ![]() $|\bar {F}_2|$ and
$|\bar {F}_2|$ and ![]() $|\bar {F}_4|$ decrease, and their main peaks move towards small
$|\bar {F}_4|$ decrease, and their main peaks move towards small ![]() ${kR}$. Nevertheless, for wave conditions around the near-trapping frequencies, i.e.
${kR}$. Nevertheless, for wave conditions around the near-trapping frequencies, i.e. ![]() ${kR}\approx 1.8$, we observe that the larger the value of
${kR}\approx 1.8$, we observe that the larger the value of ![]() $\bar {v}$, the larger the values of
$\bar {v}$, the larger the values of ![]() $|\bar {F}_2|$ and
$|\bar {F}_2|$ and ![]() $|\bar {F}_4|$. To have a better understanding of why the damping mechanism has different influences on
$|\bar {F}_4|$. To have a better understanding of why the damping mechanism has different influences on ![]() $|\bar {F}_2|$ and
$|\bar {F}_2|$ and ![]() $|\bar {F}_4|$ for the non-near-trapping and near-trapping wave conditions, we select
$|\bar {F}_4|$ for the non-near-trapping and near-trapping wave conditions, we select ![]() ${kR}=1.2$ and
${kR}=1.2$ and ![]() $1.8$ as two representative wave conditions and plot the wave scattering field in terms of wave amplitude and instantaneous free surface elevation with
$1.8$ as two representative wave conditions and plot the wave scattering field in terms of wave amplitude and instantaneous free surface elevation with ![]() $\bar {v}=0.05$ and
$\bar {v}=0.05$ and ![]() $\bar {v}=0.4$ for these two wave frequencies in figures 11 and 12, respectively. It is observed that for
$\bar {v}=0.4$ for these two wave frequencies in figures 11 and 12, respectively. It is observed that for ![]() ${kR}=1.2$ with a relatively small damping coefficient, say
${kR}=1.2$ with a relatively small damping coefficient, say ![]() $\bar {v}=0.05$ (see figures 11a and 11b), the largest and smallest wave amplitudes inside the structured cylinder are
$\bar {v}=0.05$ (see figures 11a and 11b), the largest and smallest wave amplitudes inside the structured cylinder are ![]() $|\eta ^{(0)}/A|=1.51$ and 0.67, respectively. There is one main peak of the instantaneous wave field observed inside the cylinder and the largest jump of
$|\eta ^{(0)}/A|=1.51$ and 0.67, respectively. There is one main peak of the instantaneous wave field observed inside the cylinder and the largest jump of ![]() ${\rm Re}[\eta ^{(0)}/A]$ can be as large as 1.85. As the damping coefficient increases and achieves a relatively large value, say
${\rm Re}[\eta ^{(0)}/A]$ can be as large as 1.85. As the damping coefficient increases and achieves a relatively large value, say ![]() $\bar {v}=0.4$ (see figures 11c and 11d), the free surface oscillation inside the metamaterial cylinder is effectively attenuated. The comparison between the instantaneous wave field indicates that as
$\bar {v}=0.4$ (see figures 11c and 11d), the free surface oscillation inside the metamaterial cylinder is effectively attenuated. The comparison between the instantaneous wave field indicates that as ![]() $\bar {v}$ increases from 0.05 to 0.4, the ‘wavelength’ inside the cylinder is enlarged, explaining the reason why the main peaks of
$\bar {v}$ increases from 0.05 to 0.4, the ‘wavelength’ inside the cylinder is enlarged, explaining the reason why the main peaks of ![]() $|\bar {F}_2|$ and
$|\bar {F}_2|$ and ![]() $|\bar {F}_4|$ for
$|\bar {F}_4|$ for ![]() $0.8<{kR}<1.6$ move towards small
$0.8<{kR}<1.6$ move towards small ![]() ${kR}$ with the increase of
${kR}$ with the increase of ![]() $\bar {v}$.
$\bar {v}$.
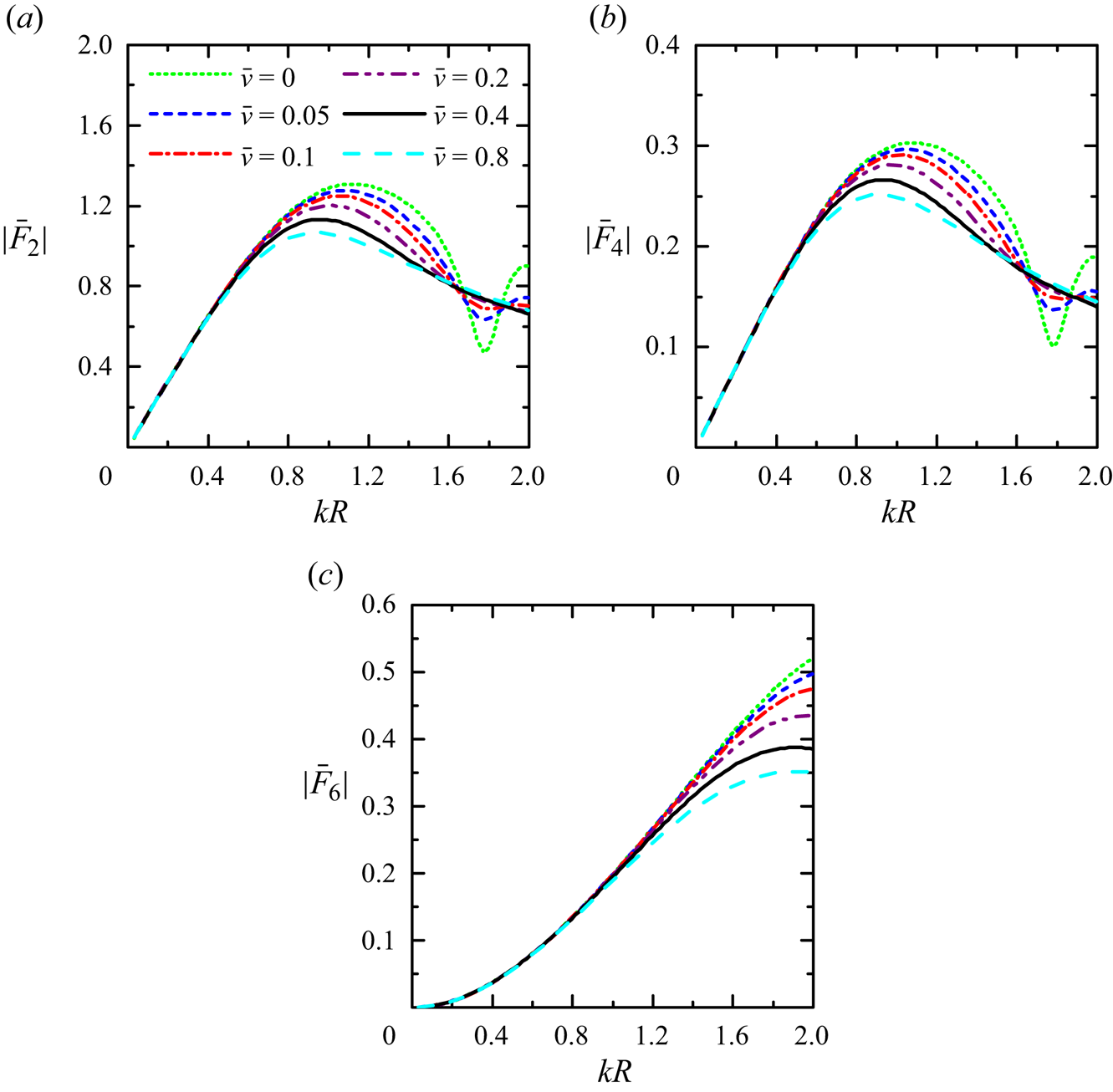
Figure 10. Frequency response of wave excitation forces experienced by a vertical truncated metamaterial cylinder (thick curves) with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.5$ and
$d/h=0.5$ and ![]() $\beta ={\rm \pi} /4$: (a)
$\beta ={\rm \pi} /4$: (a) ![]() $|\bar {F}_2|$; (b)
$|\bar {F}_2|$; (b) ![]() $|\bar {F}_4|$; (c)
$|\bar {F}_4|$; (c) ![]() $|\bar {F}_6|$.
$|\bar {F}_6|$.
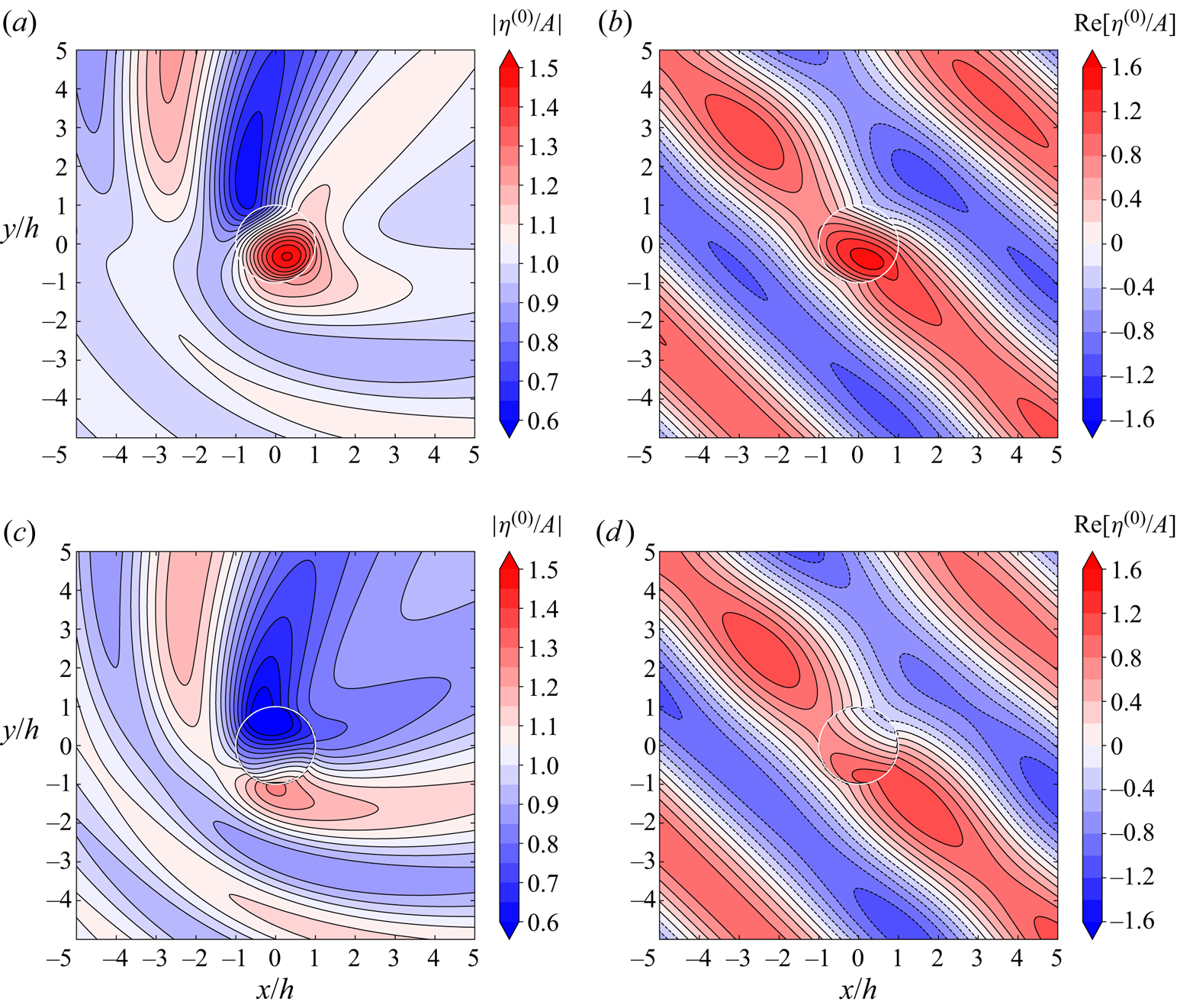
Figure 11. Wave scattering field in terms of ![]() $|\eta ^{(0)}/A|$ and
$|\eta ^{(0)}/A|$ and ![]() ${\rm Re}[\eta ^{(0)}/A]$ with
${\rm Re}[\eta ^{(0)}/A]$ with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.5$ and
$d/h=0.5$ and ![]() ${kR}=1.2$: (a) and (b)
${kR}=1.2$: (a) and (b) ![]() $\bar {v}=0.05$; (c) and (d)
$\bar {v}=0.05$; (c) and (d) ![]() $\bar {v}=0.4$. Here (a) and (c)
$\bar {v}=0.4$. Here (a) and (c) ![]() $|\eta ^{(0)}/A|$; (b) and (d)
$|\eta ^{(0)}/A|$; (b) and (d) ![]() ${\rm Re}[\eta ^{(0)}/A]$.
${\rm Re}[\eta ^{(0)}/A]$.
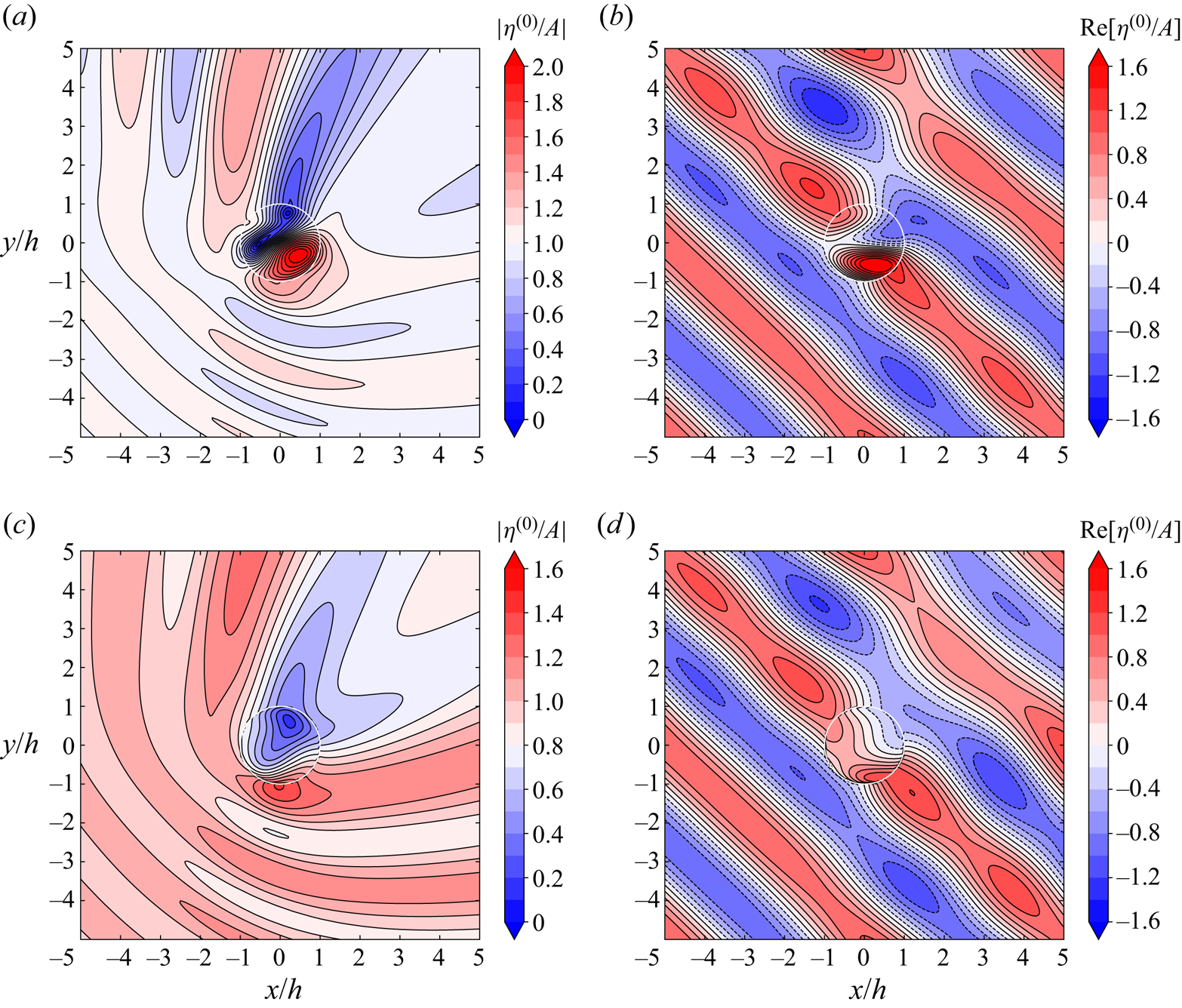
Figure 12. Wave scattering field in terms of ![]() $|\eta ^{(0)}/A|$ and
$|\eta ^{(0)}/A|$ and ![]() ${\rm Re}[\eta ^{(0)}/A]$ with
${\rm Re}[\eta ^{(0)}/A]$ with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.5$ and
$d/h=0.5$ and ![]() ${kR}=1.8$: (a) and (b)
${kR}=1.8$: (a) and (b) ![]() $\bar {v}=0.05$; (c) and (d)
$\bar {v}=0.05$; (c) and (d) ![]() $\bar {v}=0.4$. Here (a) and (c)
$\bar {v}=0.4$. Here (a) and (c) ![]() $|\eta ^{(0)}/A|$; (b) and (d)
$|\eta ^{(0)}/A|$; (b) and (d) ![]() ${\rm Re}[\eta ^{(0)}/A]$.
${\rm Re}[\eta ^{(0)}/A]$.
For the near-trapping wave conditions, say ![]() ${kR}=1.8$ (see figure 12), with a small damping coefficient, say
${kR}=1.8$ (see figure 12), with a small damping coefficient, say ![]() $\bar {v}=0.05$, there is one peak and one valley of the field of
$\bar {v}=0.05$, there is one peak and one valley of the field of ![]() $|\eta ^{(0)}/A|$ observed inside the structured cylinder. There are some strong local jumps of the instantaneous wave field across the plates inside the structured cylinder, yet after taking the integral of the jumps along the
$|\eta ^{(0)}/A|$ observed inside the structured cylinder. There are some strong local jumps of the instantaneous wave field across the plates inside the structured cylinder, yet after taking the integral of the jumps along the ![]() $y$-axis, they cancel each other out to a large extent, resulting in a relatively low value of the sway excitation force and roll excitation moment acting on the metamaterial cylinder. As
$y$-axis, they cancel each other out to a large extent, resulting in a relatively low value of the sway excitation force and roll excitation moment acting on the metamaterial cylinder. As ![]() $\bar {v}$ increases from 0.05 to 0.4, although the largest and smallest wave amplitudes inside the structured cylinder
$\bar {v}$ increases from 0.05 to 0.4, although the largest and smallest wave amplitudes inside the structured cylinder ![]() $|\eta ^{(0)}/A|$ as well as the largest jump of
$|\eta ^{(0)}/A|$ as well as the largest jump of ![]() ${\rm Re}[\eta ^{(0)}/A]$ are all decreased, the ‘wavelength’ and the pattern of the free surface inside the cylinder change, breaking the balance of the jumps along the
${\rm Re}[\eta ^{(0)}/A]$ are all decreased, the ‘wavelength’ and the pattern of the free surface inside the cylinder change, breaking the balance of the jumps along the ![]() $y$-axis and leading to large
$y$-axis and leading to large ![]() $|\bar {F}_2|$ and
$|\bar {F}_2|$ and ![]() $|\bar {F}_4|$.
$|\bar {F}_4|$.
In the computed range of ![]() $kR$, the yaw motion-related near-trapping frequencies are not covered, and the
$kR$, the yaw motion-related near-trapping frequencies are not covered, and the ![]() $|\bar {F}_6|$ is found to decrease with the increase of
$|\bar {F}_6|$ is found to decrease with the increase of ![]() $\bar {v}$ (see figure 10c).
$\bar {v}$ (see figure 10c).
Figure 13 presents the frequency response of wave radiation damping coefficients for different values of ![]() $\bar {v}$. The effect of
$\bar {v}$. The effect of ![]() $\bar {v}$ on the frequency response of
$\bar {v}$ on the frequency response of ![]() $\bar {c}_{22}$,
$\bar {c}_{22}$, ![]() $\bar {c}_{44}$ and
$\bar {c}_{44}$ and ![]() $\bar {c}_{24}$ is found to be similar to that on the frequency response of
$\bar {c}_{24}$ is found to be similar to that on the frequency response of ![]() $|\bar {F}_2|$ and
$|\bar {F}_2|$ and ![]() $|\bar {F}_4|$. We observe that
$|\bar {F}_4|$. We observe that ![]() $\bar {c}_{24}^2=\bar {c}_{22}\bar {c}_{44}$ is valid regardless of the values of
$\bar {c}_{24}^2=\bar {c}_{22}\bar {c}_{44}$ is valid regardless of the values of ![]() $\bar {v}$. The change of
$\bar {v}$. The change of ![]() $\bar {v}$ has a limited impact on
$\bar {v}$ has a limited impact on ![]() $\bar {c}_{66}$ over the examined wave conditions except for rather large wavenumbers, e.g.
$\bar {c}_{66}$ over the examined wave conditions except for rather large wavenumbers, e.g. ![]() ${kR}>1.7$, where the
${kR}>1.7$, where the ![]() $\bar {c}_{66}$-
$\bar {c}_{66}$-![]() ${kR}$ curve drops down as
${kR}$ curve drops down as ![]() $\bar {v}$ increases from 0.2 to 0.8.
$\bar {v}$ increases from 0.2 to 0.8.
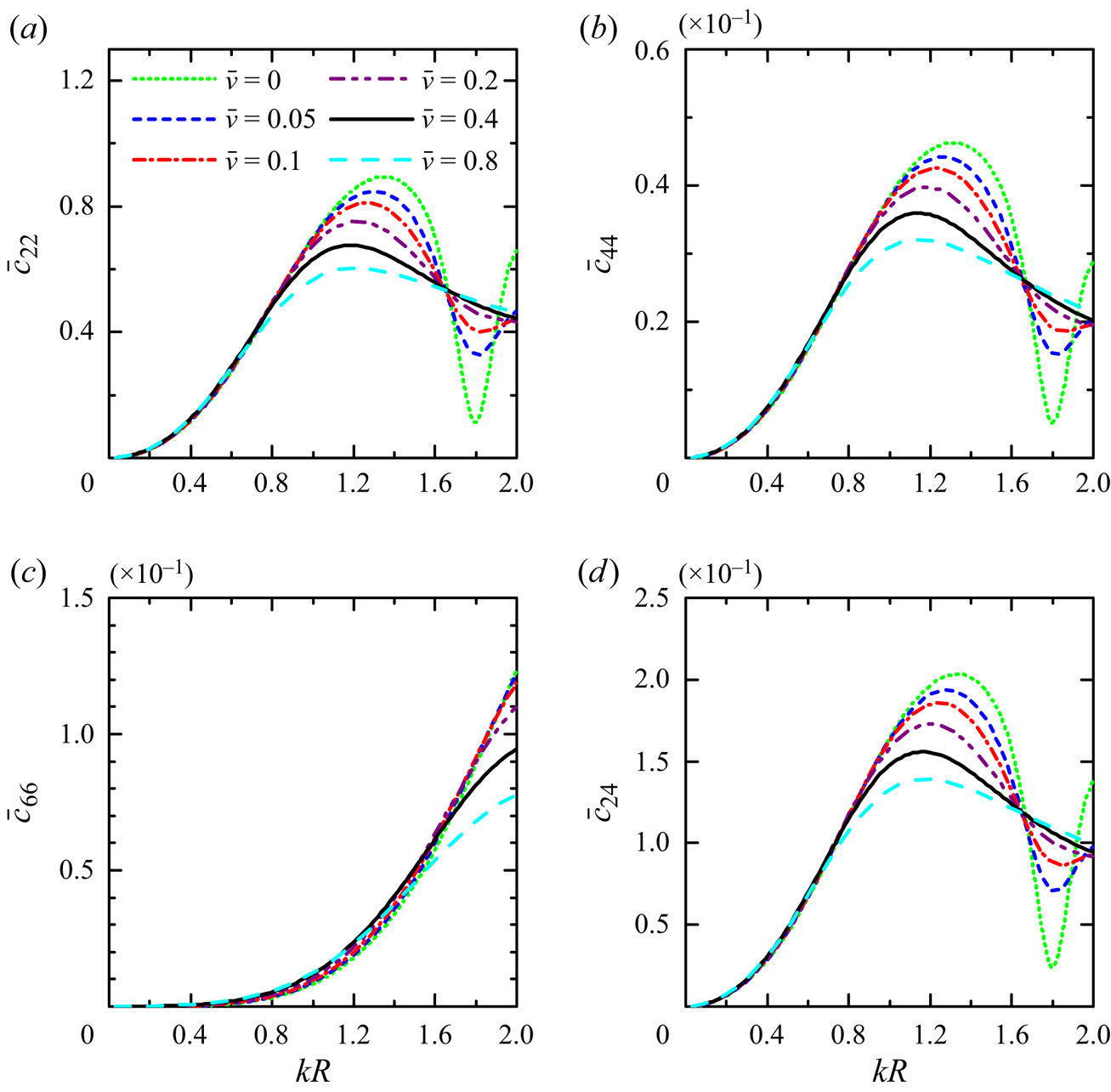
Figure 13. Frequency response of wave radiation damping of a vertical truncated metamaterial cylinder with ![]() $R/h=1.0$ and
$R/h=1.0$ and ![]() $d/h=0.5$: (a)
$d/h=0.5$: (a) ![]() $\bar {c}_{22}$; (b)
$\bar {c}_{22}$; (b) ![]() $\bar {c}_{44}$; (c)
$\bar {c}_{44}$; (c) ![]() $\bar {c}_{66}$; (d)
$\bar {c}_{66}$; (d) ![]() $\bar {c}_{24}$.
$\bar {c}_{24}$.
We also plot the frequency response of the added mass for different values of ![]() $\bar {v}$ in figure 14. The main influence of the change of
$\bar {v}$ in figure 14. The main influence of the change of ![]() $\bar {v}$ on
$\bar {v}$ on ![]() $\bar {a}_{22}$,
$\bar {a}_{22}$, ![]() $\bar {a}_{44}$ and
$\bar {a}_{44}$ and ![]() $\bar {a}_{24}$ occurs around the near-trapping frequencies
$\bar {a}_{24}$ occurs around the near-trapping frequencies ![]() ${kR}=1.8$, particularly between
${kR}=1.8$, particularly between ![]() ${kR}=1.6$ and 1.8, where the larger the
${kR}=1.6$ and 1.8, where the larger the ![]() $\bar {v}$ the larger the added masses. With the increase of
$\bar {v}$ the larger the added masses. With the increase of ![]() $\bar {v}$, the inverted ‘
$\bar {v}$, the inverted ‘![]() $N$’ shaped curves at
$N$’ shaped curves at ![]() ${kR}=1.8$ turn to be straightened, and the local peaks and valleys disappear when
${kR}=1.8$ turn to be straightened, and the local peaks and valleys disappear when ![]() $\bar {v}>0.2$. For the yaw-motion-related added mass
$\bar {v}>0.2$. For the yaw-motion-related added mass ![]() $\bar {a}_{66}$, the main peak gets lower and moves towards small
$\bar {a}_{66}$, the main peak gets lower and moves towards small ![]() ${kR}$ with the increase of the damping coefficient, which could be explained from the point of view of the enhanced attenuation and the increase of ‘wavelength’ of the wave field inside the metamaterial cylinder.
${kR}$ with the increase of the damping coefficient, which could be explained from the point of view of the enhanced attenuation and the increase of ‘wavelength’ of the wave field inside the metamaterial cylinder.
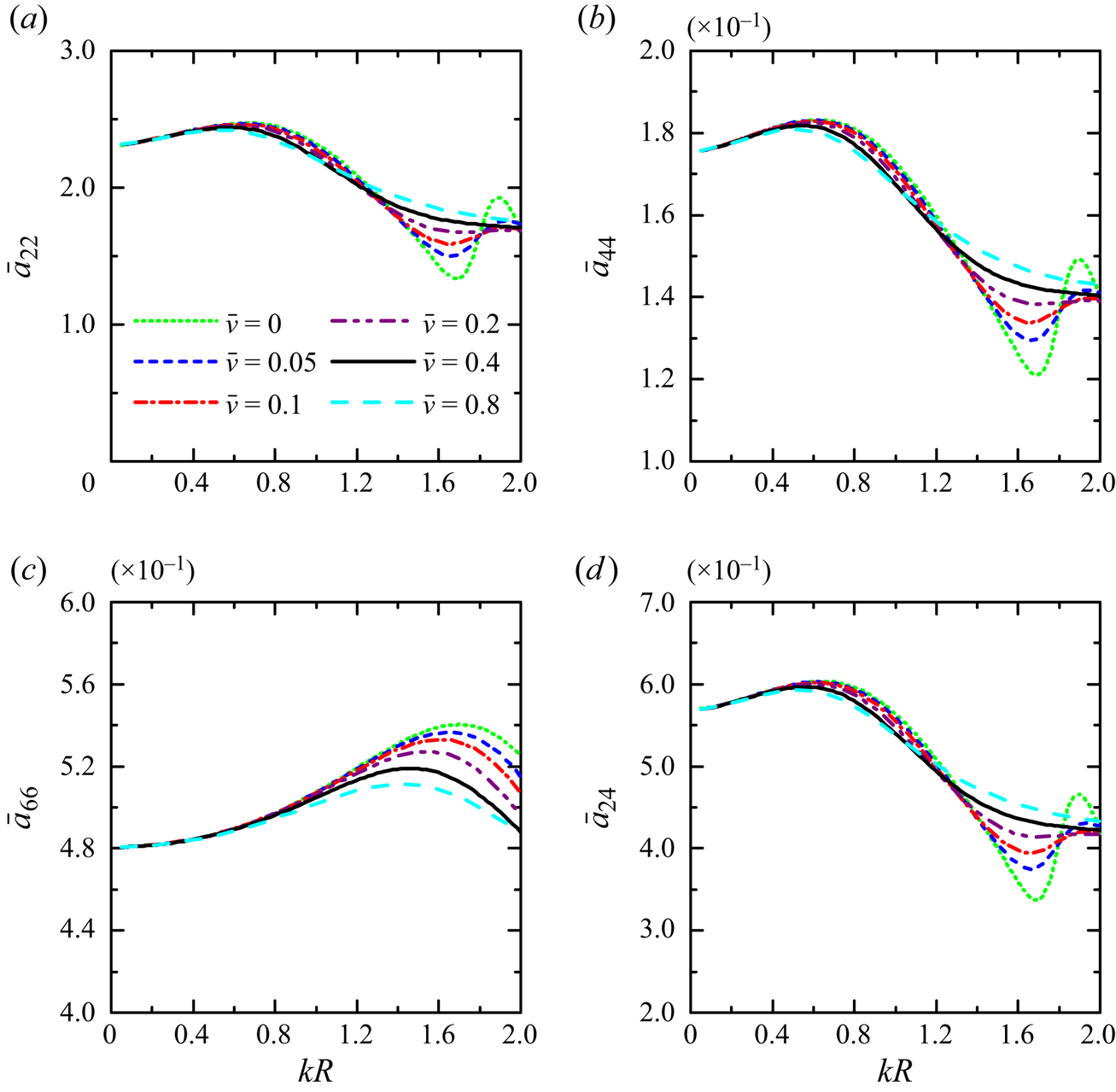
Figure 14. Frequency response of added mass of a vertical truncated metamaterial cylinder with ![]() $R/h=1.0$ and
$R/h=1.0$ and ![]() $d/h=0.5$: (a)
$d/h=0.5$: (a) ![]() $\bar {a}_{22}$; (b)
$\bar {a}_{22}$; (b) ![]() $\bar {a}_{44}$; (c)
$\bar {a}_{44}$; (c) ![]() $\bar {a}_{66}$; (d)
$\bar {a}_{66}$; (d) ![]() $\bar {a}_{24}$.
$\bar {a}_{24}$.
Finally, we examine the performance of a stationary truncated metamaterial cylinder in terms of wave power dissipation, the results of which are plotted in figure 15. For the metamaterial cylinder subjected to waves with ![]() $\beta ={\rm \pi} /4$, in the computed range of
$\beta ={\rm \pi} /4$, in the computed range of ![]() ${kR}$,
${kR}$, ![]() $\bar {P}_{diss}^{(0)}$ is monotonically increasing with the increase of
$\bar {P}_{diss}^{(0)}$ is monotonically increasing with the increase of ![]() ${kR}$ regardless of the value of
${kR}$ regardless of the value of ![]() $\bar {v}$. As
$\bar {v}$. As ![]() $\bar {v}$ increases from 0.05 to 1.6, the
$\bar {v}$ increases from 0.05 to 1.6, the ![]() $\bar {P}_{diss}^{(0)}$–
$\bar {P}_{diss}^{(0)}$–![]() ${kR}$ curve rises first and then falls after reaching the highest point, meaning that there is an optimised damping coefficient to maximise the wave power dissipation. Similar results can also be observed in figure 4(a). We then fix the damping coefficient as
${kR}$ curve rises first and then falls after reaching the highest point, meaning that there is an optimised damping coefficient to maximise the wave power dissipation. Similar results can also be observed in figure 4(a). We then fix the damping coefficient as ![]() $\bar {v}=0.4$ and examine the performance of the structured cylinder in waves with different incident wave directions. From figure 15(b) we see that the more perpendicular the plates’ alignment relative to the incident wave propagation, the more wave power can be dissipated. Note that the metamaterial cylinder may be utilised to capture wave power if the channels between the plates contain heaving buoys extracting power with their heave motion. For a traditional WEC consisting of an axisymmetric rigid cylinder moving in heave mode, the theoretical maximum wave power capture width ratio expressed in terms of
$\bar {v}=0.4$ and examine the performance of the structured cylinder in waves with different incident wave directions. From figure 15(b) we see that the more perpendicular the plates’ alignment relative to the incident wave propagation, the more wave power can be dissipated. Note that the metamaterial cylinder may be utilised to capture wave power if the channels between the plates contain heaving buoys extracting power with their heave motion. For a traditional WEC consisting of an axisymmetric rigid cylinder moving in heave mode, the theoretical maximum wave power capture width ratio expressed in terms of ![]() $\bar {P}_{diss}^{(0)}$ is 1.0 when the motion is fully optimised (e.g. see Budal & Falnes Reference Budal and Falnes1975; Evans Reference Evans1976; Newman Reference Newman1976). The metamaterial cylinder with
$\bar {P}_{diss}^{(0)}$ is 1.0 when the motion is fully optimised (e.g. see Budal & Falnes Reference Budal and Falnes1975; Evans Reference Evans1976; Newman Reference Newman1976). The metamaterial cylinder with ![]() $\bar {v}=0.4$ especially for
$\bar {v}=0.4$ especially for ![]() $\beta ={\rm \pi} /2$ is able to give
$\beta ={\rm \pi} /2$ is able to give ![]() $\bar {P}_{diss}^{(0)}>1.0$ over a wide range of wave conditions, absorbing more than a traditional axisymmetric heaving WEC can achieve. Applying heaving buoys with a metamaterial cylinder consisting of a series of parallel plates is merely a concept for wave power absorption. There are also some other concepts of harnessing wave power with a metamaterial cylinder, e.g. using a pair of opposing vertically buoyant hinged paddles oscillating along the centre plane of the narrow channels to capture wave power (Huang & Porter Reference Huang and Porter2022), and more recently, employing an array of small cuboid buoys inside a surface-piercing truncated metamaterial cylinder consisting of two overlapping arrays of closely spaced vertical thin plates to absorb wave power (Huang, Porter & Zheng Reference Huang, Porter and Zheng2023).
$\bar {P}_{diss}^{(0)}>1.0$ over a wide range of wave conditions, absorbing more than a traditional axisymmetric heaving WEC can achieve. Applying heaving buoys with a metamaterial cylinder consisting of a series of parallel plates is merely a concept for wave power absorption. There are also some other concepts of harnessing wave power with a metamaterial cylinder, e.g. using a pair of opposing vertically buoyant hinged paddles oscillating along the centre plane of the narrow channels to capture wave power (Huang & Porter Reference Huang and Porter2022), and more recently, employing an array of small cuboid buoys inside a surface-piercing truncated metamaterial cylinder consisting of two overlapping arrays of closely spaced vertical thin plates to absorb wave power (Huang, Porter & Zheng Reference Huang, Porter and Zheng2023).
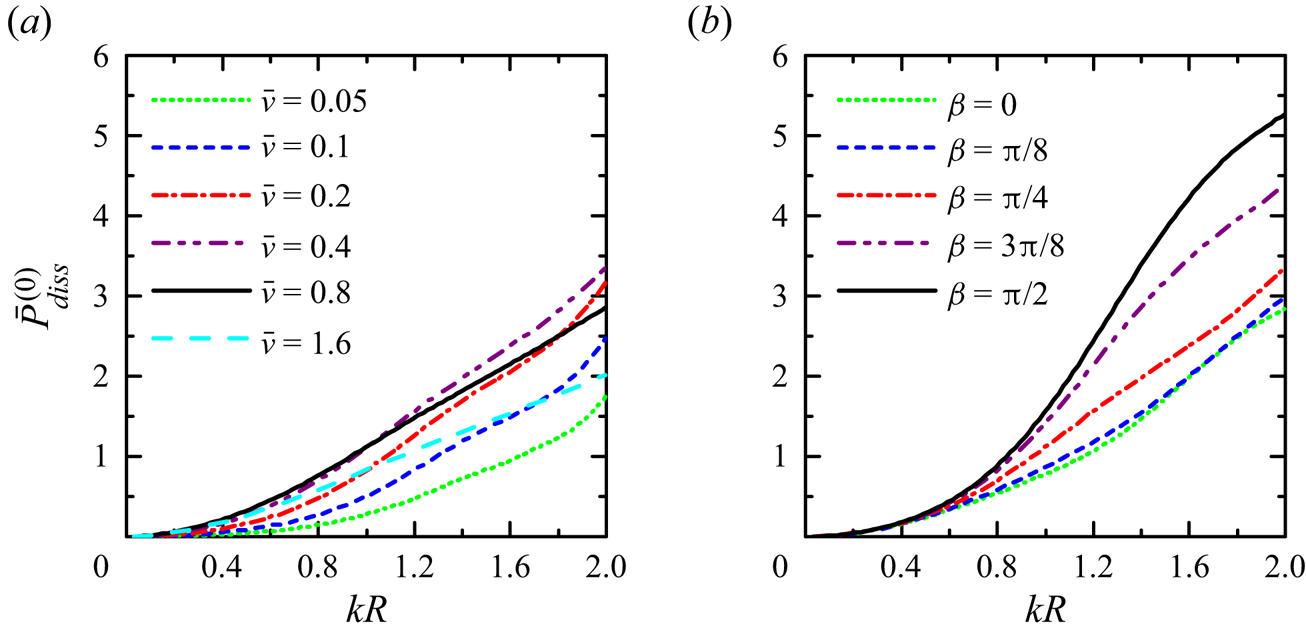
Figure 15. Frequency response of the non-dimensional dissipated wave power of a stationary vertical truncated metamaterial cylinder with ![]() $R/h=1.0$ and
$R/h=1.0$ and ![]() $d/h=0.5$: (a)
$d/h=0.5$: (a) ![]() $\bar {P}_{diss}^{(0)}$ for
$\bar {P}_{diss}^{(0)}$ for ![]() $\beta ={\rm \pi} /4$; (b)
$\beta ={\rm \pi} /4$; (b) ![]() $\bar {P}_{diss}^{(0)}$ for
$\bar {P}_{diss}^{(0)}$ for ![]() $\bar {v}=0.4$.
$\bar {v}=0.4$.
6. Conclusions
In this paper, we have considered scattering and radiation of water waves by a surface-piercing vertical truncated metamaterial cylinder, which is composed of a closely spaced array of thin vertical barriers. The fluids inside the truncated metamaterial cylinder are allowed and restricted by the barriers to flow between them and parallel to them. A theoretical model based on linear velocity flow theory is developed to solve the hydrodynamic problems, in which an effective medium equation is employed to describe the wave motion inside the cylinder.
We have proved and confirmed that the wave excitation forces acting on the metamaterial cylinder can be expressed not only in terms of the local interior or exterior velocity potential straightforwardly but also in terms of the far-field radiation coefficients. Moreover, there is a reciprocity relation between radiation damping and excitation forces/far-field radiation coefficients. It is revealed that the frequency responses of the sway excitation force, the sway–sway radiation damping, and the sway–sway added mass of the truncated metamaterial cylinder have a similar appearance to those of the equivalent truncated solid cylinder, except at near-trapping frequencies, where a sharp valley of the sway excitation force and radiation damping curves happens, whereas an inverted ‘![]() $N$’ shaped curve is observed for the sway–sway added mass. For small wavenumbers, the radiated wave field around a metamaterial cylinder oscillating in sway performs in a dipolar pattern; whereas, for the yaw-motion case, the radiated wave field is dominated by the
$N$’ shaped curve is observed for the sway–sway added mass. For small wavenumbers, the radiated wave field around a metamaterial cylinder oscillating in sway performs in a dipolar pattern; whereas, for the yaw-motion case, the radiated wave field is dominated by the ![]() $\sin (2\theta )$ circular components. Large-amplitude wave motion can be excited inside the metamaterial cylinder when the oscillating frequencies are close to the near-trapping frequencies. The yaw motion-related near-trapping frequencies are generally larger than those of the sway and roll ones.
$\sin (2\theta )$ circular components. Large-amplitude wave motion can be excited inside the metamaterial cylinder when the oscillating frequencies are close to the near-trapping frequencies. The yaw motion-related near-trapping frequencies are generally larger than those of the sway and roll ones.
The sway excitation force and roll excitation moment acting on the metamaterial cylinder for non-near-trapping wave frequencies can be effectively reduced by inducing a damping mechanism at the free surface inside the cylinder. The larger the damping coefficient, the lower the main peaks of their frequency responses, and those peaks move towards small wave frequencies. Nevertheless, for the near-trapping frequencies, the sway and roll excitation force/moment increase with the increase of the damping coefficient. The truncated metamaterial cylinder when fixed in place and with a damping mechanism included is found to dissipate more wave power when the plates are aligned more perpendicular relative to the incident wave propagation. The metamaterial cylinder is able to capture more wave power than that of a traditional axisymmetric heaving WEC over a wide range of wave frequencies.
The model developed, as well as the findings revealed, in this paper could be of significant value for deepening understanding of water wave interaction with floating metamaterial structures, shedding light on the harnessing and dissipation of wave energy with the employment of metamaterials.
Funding
The research was supported by the Open Research Fund Program of the State Key Laboratory of Hydroscience and Engineering (Tsinghua University) (grant number sklhse-2021-E-02). D.G. gratefully acknowledges the EPSRC for supporting part of this work through the Supergen ORE Hub, EP/S000747/1.
Declaration of interests
The authors report no conflict of interest.
Appendix A. Some useful integrals based on Green's theorem
Figure 16 presents a sketch of a finite region of the sea containing a surface-piercing vertical truncated metamaterial cylinder. Figure 16(a) shows the finite 3-D region outside the structured cylinder. It is assumed that outside the region, the sea is unbounded horizontally and the water has a constant depth ![]() $h$ outside the mentioned finite region. Figure 16(b) illustrates the 2-D fluid domain inside a narrow channel between the closely spaced barriers.
$h$ outside the mentioned finite region. Figure 16(b) illustrates the 2-D fluid domain inside a narrow channel between the closely spaced barriers.
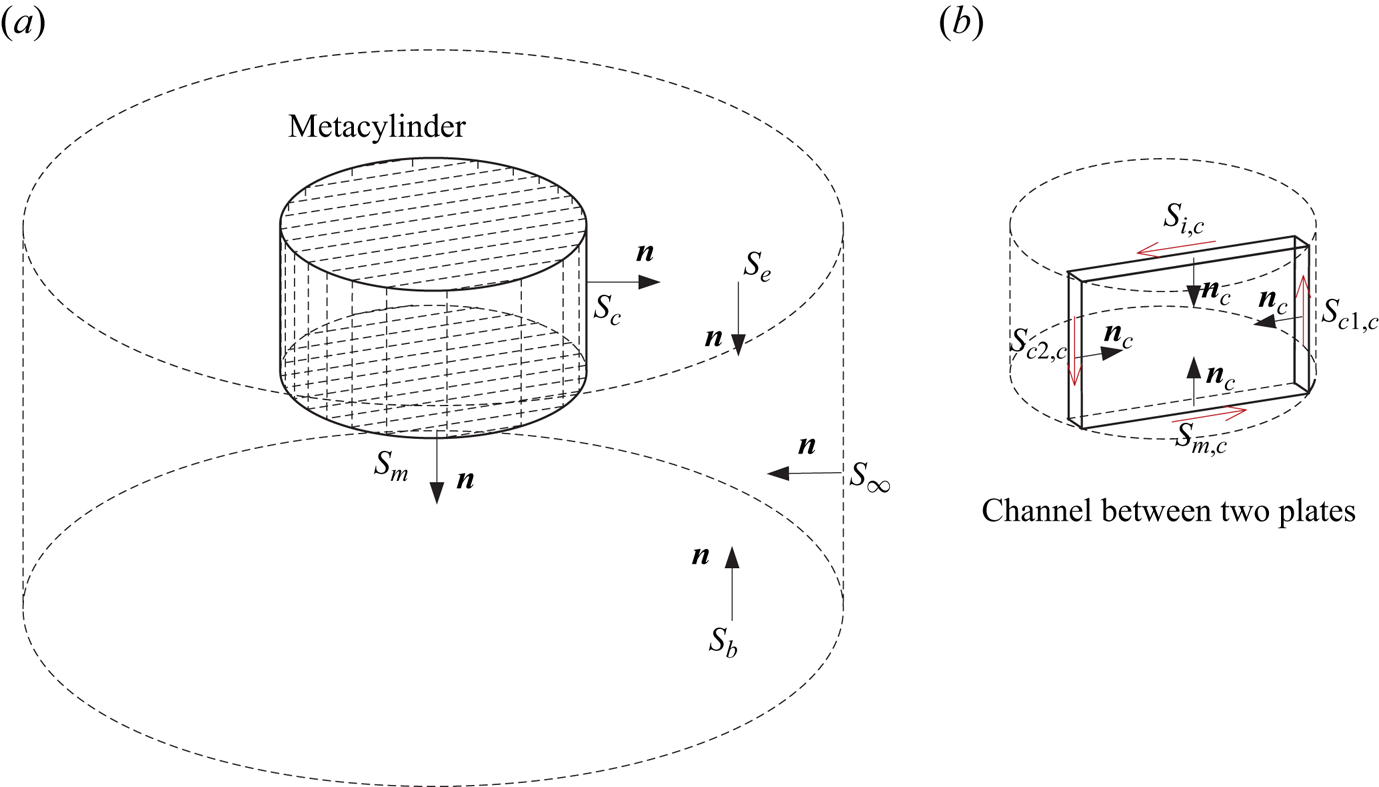
Figure 16. (a) A truncated metamaterial cylinder within an imaginary cylindrical control surface ![]() $S_{\infty }$. Wetted curved cylindrical sidewall and bottom of the metamaterial cylinder are indicated by
$S_{\infty }$. Wetted curved cylindrical sidewall and bottom of the metamaterial cylinder are indicated by ![]() $S_c$ and
$S_c$ and ![]() $S_m$, whereas
$S_m$, whereas ![]() $S_e$ denotes the external water surface. (b) A channel between two adjacent barriers of the metamaterial cylinder. Side opening and bottom of the channel are indicated by
$S_e$ denotes the external water surface. (b) A channel between two adjacent barriers of the metamaterial cylinder. Side opening and bottom of the channel are indicated by ![]() $S_{c1,c}$,
$S_{c1,c}$, ![]() $S_{c2,c}$ and
$S_{c2,c}$ and ![]() $S_{m,c}$, whereas
$S_{m,c}$, whereas ![]() $S_{i,c}$ denotes the internal water surface. The red arrows indicate the direction of the line integrals.
$S_{i,c}$ denotes the internal water surface. The red arrows indicate the direction of the line integrals.
Let us now apply Green's theorem to the 3-D and 2-D fluid regions indicated in figure 16. As shown in figure 16, the 3-D fluid region is contained inside a closed surface composed of the curved sidewall of the cylinder, ![]() $S_c$, the circular bottom of the cylinder,
$S_c$, the circular bottom of the cylinder, ![]() $S_m$, the free water surface external to the cylinder,
$S_m$, the free water surface external to the cylinder, ![]() $S_e$, the sea bed,
$S_e$, the sea bed, ![]() $S_b$, and an envisaged vertical cylinder-shaped ‘control’ surface at
$S_b$, and an envisaged vertical cylinder-shaped ‘control’ surface at ![]() $r\rightarrow \infty$,
$r\rightarrow \infty$, ![]() $S_{\infty }$.
$S_{\infty }$.
We define a useful integral over the curved sidewall of the cylinder and the circular bottom of the cylinder
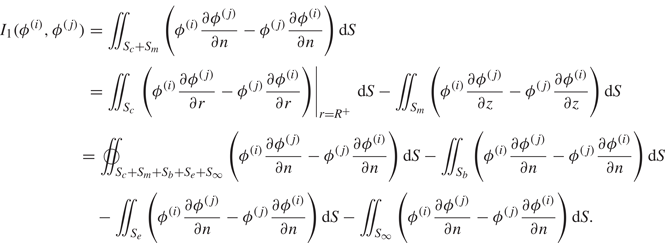 \begin{align} I_1(\phi^{(i)},\phi^{(\,j)})&=\iint_{S_c+S_m}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S\nonumber\\ &=\iint_{S_c}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial r}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial r}\right)\right|_{r=R^+}\, {\rm d}S-\iint_{S_m}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial z}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial z}\right) {\rm d}S \nonumber\\ &=\unicode{x222F}_{S_c+S_m+S_b+S_e+S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S-\iint_{S_b}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S\nonumber\\ &\quad -\iint_{S_e}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S-\iint_{S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S. \end{align}
\begin{align} I_1(\phi^{(i)},\phi^{(\,j)})&=\iint_{S_c+S_m}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S\nonumber\\ &=\iint_{S_c}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial r}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial r}\right)\right|_{r=R^+}\, {\rm d}S-\iint_{S_m}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial z}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial z}\right) {\rm d}S \nonumber\\ &=\unicode{x222F}_{S_c+S_m+S_b+S_e+S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S-\iint_{S_b}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S\nonumber\\ &\quad -\iint_{S_e}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S-\iint_{S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S. \end{align} Following from Gauss’ divergence theorem, the surface integral of a vector field over a closed surface, i.e. the flux through the surface, is equal to the volume integral of the divergence over the region inside the surface, and since both ![]() $\phi ^{(i)}$ and
$\phi ^{(i)}$ and ![]() $\phi ^{(\,j)}$ satisfy Laplace's equation all over the fluid domain, we have
$\phi ^{(\,j)}$ satisfy Laplace's equation all over the fluid domain, we have
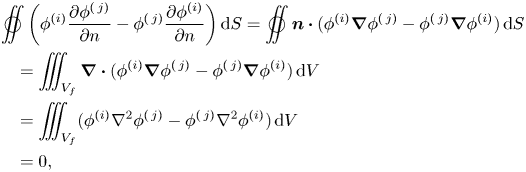 \begin{align} &\unicode{x222F}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S=\unicode{x222F} \boldsymbol{n}\boldsymbol{\cdot} (\phi^{(i)}\boldsymbol{\nabla} \phi^{(\,j)}-\phi^{(\,j)}\boldsymbol{\nabla} \phi^{(i)})\,{\rm d}S\nonumber\\ &\quad =\iiint_{V_f} \boldsymbol{\nabla}\boldsymbol{\cdot}(\phi^{(i)}\boldsymbol{\nabla} \phi^{(\,j)}-\phi^{(\,j)}\boldsymbol{\nabla} \phi^{(i)})\,{\rm d}V\nonumber\\ &\quad =\iiint_{V_f} (\phi^{(i)}\nabla^2 \phi^{(\,j)}-\phi^{(\,j)}\nabla^2 \phi^{(i)})\,{\rm d}V\nonumber\\ &\quad =0, \end{align}
\begin{align} &\unicode{x222F}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n}\right) {\rm d}S=\unicode{x222F} \boldsymbol{n}\boldsymbol{\cdot} (\phi^{(i)}\boldsymbol{\nabla} \phi^{(\,j)}-\phi^{(\,j)}\boldsymbol{\nabla} \phi^{(i)})\,{\rm d}S\nonumber\\ &\quad =\iiint_{V_f} \boldsymbol{\nabla}\boldsymbol{\cdot}(\phi^{(i)}\boldsymbol{\nabla} \phi^{(\,j)}-\phi^{(\,j)}\boldsymbol{\nabla} \phi^{(i)})\,{\rm d}V\nonumber\\ &\quad =\iiint_{V_f} (\phi^{(i)}\nabla^2 \phi^{(\,j)}-\phi^{(\,j)}\nabla^2 \phi^{(i)})\,{\rm d}V\nonumber\\ &\quad =0, \end{align}
where ![]() $V_f$ denotes the fluid volume enclosed by the closed surface.
$V_f$ denotes the fluid volume enclosed by the closed surface.
Note also that the integrand in (A1) vanishes on ![]() $S_b$ and
$S_b$ and ![]() $S_e$ because of the free surface and seabed boundary conditions (2.5) and (2.6). Hence, instead of integrating over
$S_e$ because of the free surface and seabed boundary conditions (2.5) and (2.6). Hence, instead of integrating over ![]() $S_c$ and
$S_c$ and ![]() $S_m$, we may express
$S_m$, we may express ![]() $I_1(\phi ^{(i)},\phi ^{(\,j)})$ by integrating over
$I_1(\phi ^{(i)},\phi ^{(\,j)})$ by integrating over ![]() $S_{\infty }$,
$S_{\infty }$,
For ![]() $i,j \neq 0$, we have
$i,j \neq 0$, we have ![]() $I_1(\phi ^{(i)},\phi ^{(\,j)})=0$ because
$I_1(\phi ^{(i)},\phi ^{(\,j)})=0$ because ![]() $\phi ^{(i)}$ and
$\phi ^{(i)}$ and ![]() $\phi ^{(\,j)}$ satisfy the same radiation conditions. However, because
$\phi ^{(\,j)}$ satisfy the same radiation conditions. However, because ![]() $\phi ^{(i)}$ and
$\phi ^{(i)}$ and ![]() $\phi ^{(\,j)*}$ satisfy opposite radiation conditions, we have
$\phi ^{(\,j)*}$ satisfy opposite radiation conditions, we have
Similarly, we define another useful integral over the two opening sides and the bottom of a narrow channel (see figure 16b) located at ![]() $y$,
$y$,
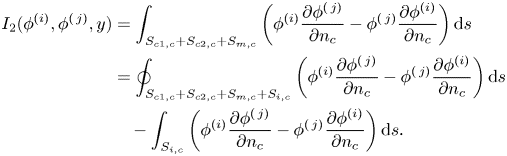 \begin{align} I_2(\phi^{(i)},\phi^{(\,j)},y)&=\int_{S_{c1,c}+S_{c2,c}+S_{m,c}} \left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s\nonumber\\ &=\oint_{S_{c1,c}+S_{c2,c}+S_{m,c}+S_{i,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s\nonumber\\ &\quad-\int_{S_{i,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s. \end{align}
\begin{align} I_2(\phi^{(i)},\phi^{(\,j)},y)&=\int_{S_{c1,c}+S_{c2,c}+S_{m,c}} \left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s\nonumber\\ &=\oint_{S_{c1,c}+S_{c2,c}+S_{m,c}+S_{i,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s\nonumber\\ &\quad-\int_{S_{i,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s. \end{align} Following from the 2-D divergence theorem, the integral of a vector field over a closed line is equal to the surface integral of the divergence over the area enclosed by the line. Since both ![]() $\phi ^{(i)}$ and
$\phi ^{(i)}$ and ![]() $\phi ^{(\,j)}$ satisfy the reduced Laplace equation, i.e. (2.2), inside the channel, we have
$\phi ^{(\,j)}$ satisfy the reduced Laplace equation, i.e. (2.2), inside the channel, we have
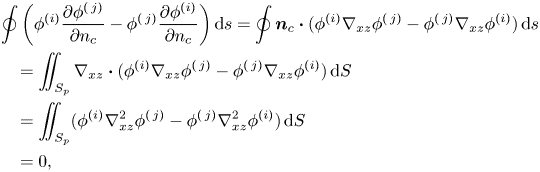 \begin{align} &\oint \left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s= \oint \boldsymbol{n}_c\boldsymbol{\cdot}(\phi^{(i)}\nabla_{xz} \phi^{(\,j)}-\phi^{(\,j)}\nabla_{xz} \phi^{(i)})\, {\rm d}s\nonumber\\ &\quad =\iint_{S_p}\nabla_{xz}\boldsymbol{\cdot} (\phi^{(i)}\nabla_{xz} \phi^{(\,j)}-\phi^{(\,j)}\nabla_{xz} \phi^{(i)})\,{\rm d}S\nonumber\\ &\quad =\iint_{S_p} (\phi^{(i)}\nabla_{xz}^2 \phi^{(\,j)}-\phi^{(\,j)}\nabla_{xz}^2 \phi^{(i)})\,{\rm d}S\nonumber\\ &\quad =0, \end{align}
\begin{align} &\oint \left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s= \oint \boldsymbol{n}_c\boldsymbol{\cdot}(\phi^{(i)}\nabla_{xz} \phi^{(\,j)}-\phi^{(\,j)}\nabla_{xz} \phi^{(i)})\, {\rm d}s\nonumber\\ &\quad =\iint_{S_p}\nabla_{xz}\boldsymbol{\cdot} (\phi^{(i)}\nabla_{xz} \phi^{(\,j)}-\phi^{(\,j)}\nabla_{xz} \phi^{(i)})\,{\rm d}S\nonumber\\ &\quad =\iint_{S_p} (\phi^{(i)}\nabla_{xz}^2 \phi^{(\,j)}-\phi^{(\,j)}\nabla_{xz}^2 \phi^{(i)})\,{\rm d}S\nonumber\\ &\quad =0, \end{align}
where ![]() $S_p$ denotes the barrier region at
$S_p$ denotes the barrier region at ![]() $y$.
$y$.
Note that the integrand in (A5) vanishes on ![]() $S_{i,c}$ because of the free surface boundary condition, (2.4), leading to
$S_{i,c}$ because of the free surface boundary condition, (2.4), leading to
Because ![]() $\phi ^{(i)}$ and
$\phi ^{(i)}$ and ![]() $\phi ^{(\,j)*}$ satisfy different free surface conditions inside the cylinder, we have
$\phi ^{(\,j)*}$ satisfy different free surface conditions inside the cylinder, we have
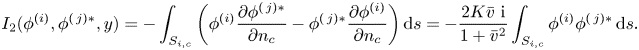 \begin{align} I_2(\phi^{(i)},\phi^{(\,j)*},y)=-\int_{S_{i,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial n_c}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s=-\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\int_{S_{i,c}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}s. \end{align}
\begin{align} I_2(\phi^{(i)},\phi^{(\,j)*},y)=-\int_{S_{i,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial n_c}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s=-\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\int_{S_{i,c}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}s. \end{align} After integrating ![]() $I_2(\phi ^{(i)},\phi ^{(\,j)},y)$ and
$I_2(\phi ^{(i)},\phi ^{(\,j)},y)$ and ![]() $I_2(\phi ^{(i)},\phi ^{(\,j)*},y)$ over the
$I_2(\phi ^{(i)},\phi ^{(\,j)*},y)$ over the ![]() $y$ dimension of the metamaterial cylinder, we have
$y$ dimension of the metamaterial cylinder, we have
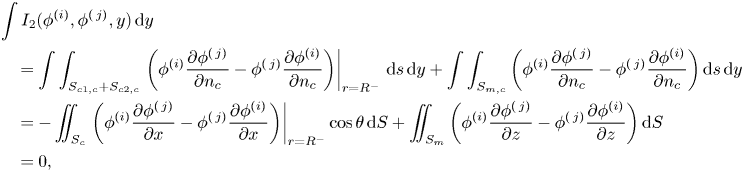 \begin{align} &\int I_2(\phi^{(i)},\phi^{(\,j)},y)\, {\rm d} y\nonumber\\ &\quad =\int \int_{S_{c1,c}+S_{c2,c}}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right)\right|_{r=R^-}\, {\rm d}s\,{\rm d} y+\int \int_{S_{m,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s \,{\rm d} y\nonumber\\ &\quad =-\iint_{S_{c}}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial x}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial x}\right) \right|_{r=R^-} \cos \theta \,{\rm d}S + \iint_{S_{m}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial z}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial z}\right) {\rm d}S\nonumber\\ &\quad =0, \end{align}
\begin{align} &\int I_2(\phi^{(i)},\phi^{(\,j)},y)\, {\rm d} y\nonumber\\ &\quad =\int \int_{S_{c1,c}+S_{c2,c}}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right)\right|_{r=R^-}\, {\rm d}s\,{\rm d} y+\int \int_{S_{m,c}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial n_c}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial n_c}\right) {\rm d}s \,{\rm d} y\nonumber\\ &\quad =-\iint_{S_{c}}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial x}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial x}\right) \right|_{r=R^-} \cos \theta \,{\rm d}S + \iint_{S_{m}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial z}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial z}\right) {\rm d}S\nonumber\\ &\quad =0, \end{align}and
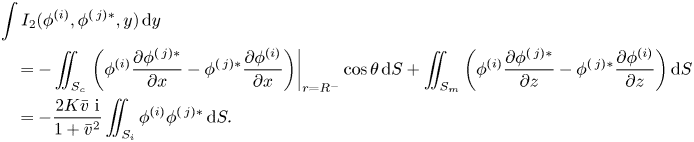 \begin{align} &\int I_2(\phi^{(i)},\phi^{(\,j)*},y)\, {\rm d} y\nonumber\\ &\quad =-\iint_{S_{c}}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial x}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial x}\right) \right|_{r=R^-} \cos \theta \,{\rm d}S + \iint_{S_{m}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial z}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial z}\right) {\rm d}S\nonumber\\ &\quad =-\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}S. \end{align}
\begin{align} &\int I_2(\phi^{(i)},\phi^{(\,j)*},y)\, {\rm d} y\nonumber\\ &\quad =-\iint_{S_{c}}\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial x}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial x}\right) \right|_{r=R^-} \cos \theta \,{\rm d}S + \iint_{S_{m}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial z}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial z}\right) {\rm d}S\nonumber\\ &\quad =-\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}S. \end{align}After taking the sum of (A3) and (A9), and applying the continuum boundary of velocity over the curved surface of the cylinder, (2.8b), we have
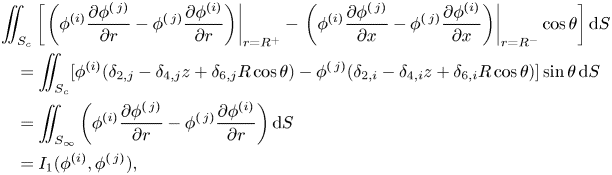 \begin{align} & \iint_{S_c}\left[\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial r}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial r}\right)\right|_{r=R^+}-\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial x}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial x}\right)\right|_{r=R^-} \cos \theta \right] {\rm d}S\nonumber\\ &\quad =\iint_{S_c}[\phi^{(i)}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos \theta) -\phi^{(\,j)}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos \theta) ]\sin \theta \,{\rm d}S\nonumber\\ &\quad =\iint_{S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial r}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial r}\right) {\rm d}S\nonumber\\ &\quad =I_1(\phi^{(i)},\phi^{(\,j)}), \end{align}
\begin{align} & \iint_{S_c}\left[\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial r}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial r}\right)\right|_{r=R^+}-\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial x}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial x}\right)\right|_{r=R^-} \cos \theta \right] {\rm d}S\nonumber\\ &\quad =\iint_{S_c}[\phi^{(i)}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos \theta) -\phi^{(\,j)}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos \theta) ]\sin \theta \,{\rm d}S\nonumber\\ &\quad =\iint_{S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)}}{\partial r}-\phi^{(\,j)}\frac{\partial \phi^{(i)}}{\partial r}\right) {\rm d}S\nonumber\\ &\quad =I_1(\phi^{(i)},\phi^{(\,j)}), \end{align}and, similarly, by using (A4) and (A10), together with (2.8b), we have
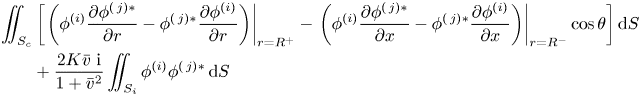 \begin{align} & \iint_{S_c}\left[\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial r}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial r}\right)\right|_{r=R^+}-\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial x}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial x}\right)\right|_{r=R^-} \cos \theta \right] {\rm d}S\nonumber\\ &\qquad+\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}S \nonumber\\ &\quad =\iint_{S_c}[\phi^{(i)}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos \theta)-\phi^{(\,j)*}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos \theta) ] \sin \theta \,{\rm d}S\nonumber\\ &\qquad+\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}S\nonumber\\ &\quad =\iint_{S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial r}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial r}\right) {\rm d}S\nonumber\\ &\quad =I_1(\phi^{(i)},\phi^{(\,j)*}). \end{align}
\begin{align} & \iint_{S_c}\left[\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial r}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial r}\right)\right|_{r=R^+}-\left.\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial x}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial x}\right)\right|_{r=R^-} \cos \theta \right] {\rm d}S\nonumber\\ &\qquad+\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}S \nonumber\\ &\quad =\iint_{S_c}[\phi^{(i)}(\delta_{2,j}-\delta_{4,j}z+\delta_{6,j}R\cos \theta)-\phi^{(\,j)*}(\delta_{2,i}-\delta_{4,i}z+\delta_{6,i}R\cos \theta) ] \sin \theta \,{\rm d}S\nonumber\\ &\qquad+\frac{2K\bar{v}\ \mathrm{i}}{1+\bar{v}^2}\iint_{S_{i}}\phi^{(i)}\phi^{(\,j)*}\, {\rm d}S\nonumber\\ &\quad =\iint_{S_{\infty}}\left(\phi^{(i)}\frac{\partial \phi^{(\,j)*}}{\partial r}-\phi^{(\,j)*}\frac{\partial \phi^{(i)}}{\partial r}\right) {\rm d}S\nonumber\\ &\quad =I_1(\phi^{(i)},\phi^{(\,j)*}). \end{align}Appendix B. Convergence analysis
Figures 17 and 18 illustrate the impact of the angular cut-offs and vertical cut-offs in terms of ![]() $M$ (
$M$ (![]() $m=-M, \ldots, M$) and
$m=-M, \ldots, M$) and ![]() $L$ (
$L$ (![]() $l=0, 1, \ldots, L$), respectively, on the frequency responses of wave excitation forces. In order to obtain the converged results,
$l=0, 1, \ldots, L$), respectively, on the frequency responses of wave excitation forces. In order to obtain the converged results, ![]() $M \ge 5$ and
$M \ge 5$ and ![]() $L \ge 4$ are suggested.
$L \ge 4$ are suggested.
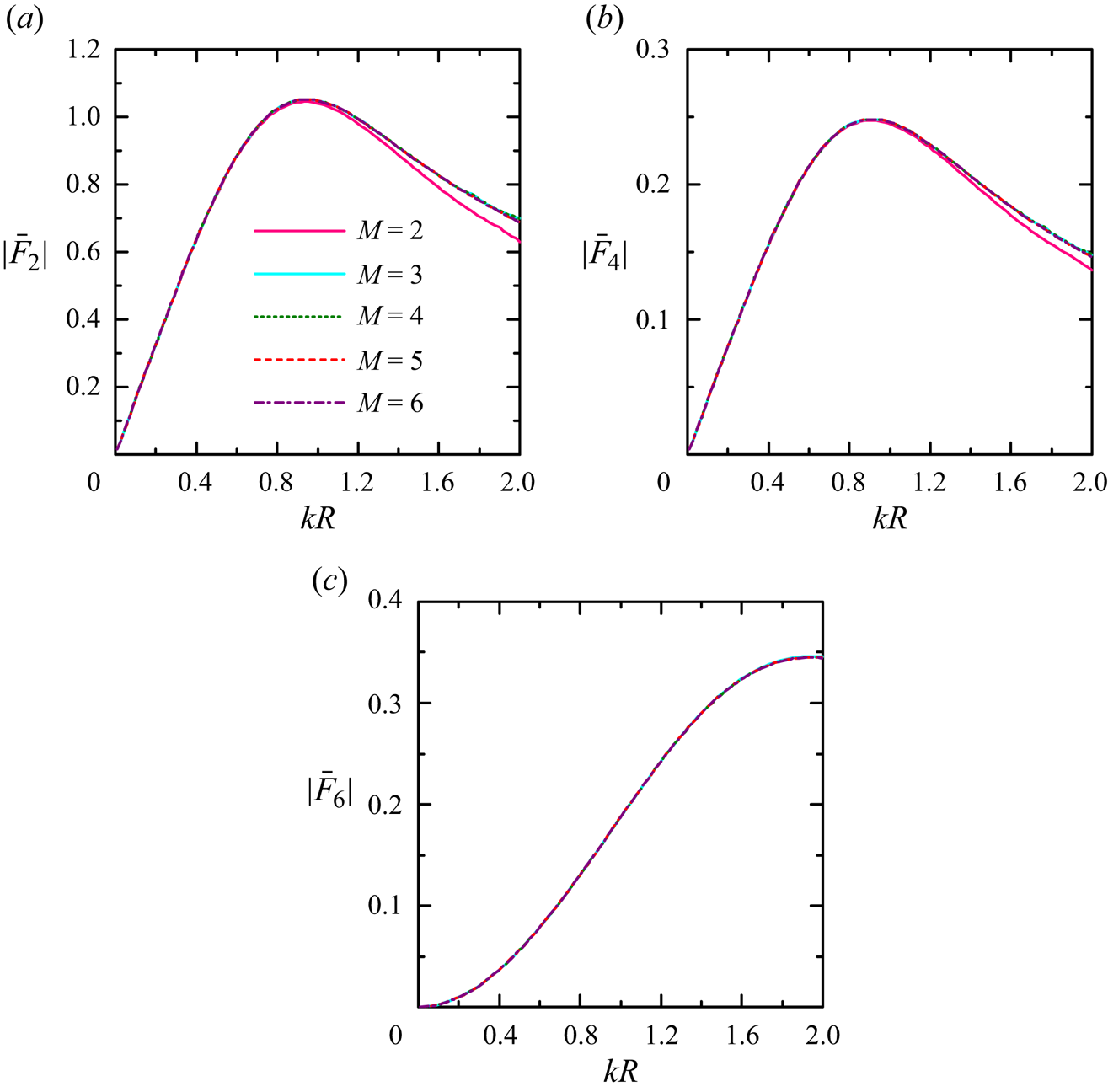
Figure 17. Impact of the angular cut-offs (i.e. in terms of ![]() $M$) on wave excitation forces acting on vertical truncated metamaterial cylinder with
$M$) on wave excitation forces acting on vertical truncated metamaterial cylinder with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.5$,
$d/h=0.5$, ![]() $\bar {v}=1.0$,
$\bar {v}=1.0$, ![]() $\beta ={\rm \pi} /4$, and
$\beta ={\rm \pi} /4$, and ![]() $L=4$: (a)
$L=4$: (a) ![]() $|\bar {F}_2|$; (b)
$|\bar {F}_2|$; (b) ![]() $|\bar {F}_4|$ and (c)
$|\bar {F}_4|$ and (c) ![]() $|\bar {F}_6|$.
$|\bar {F}_6|$.
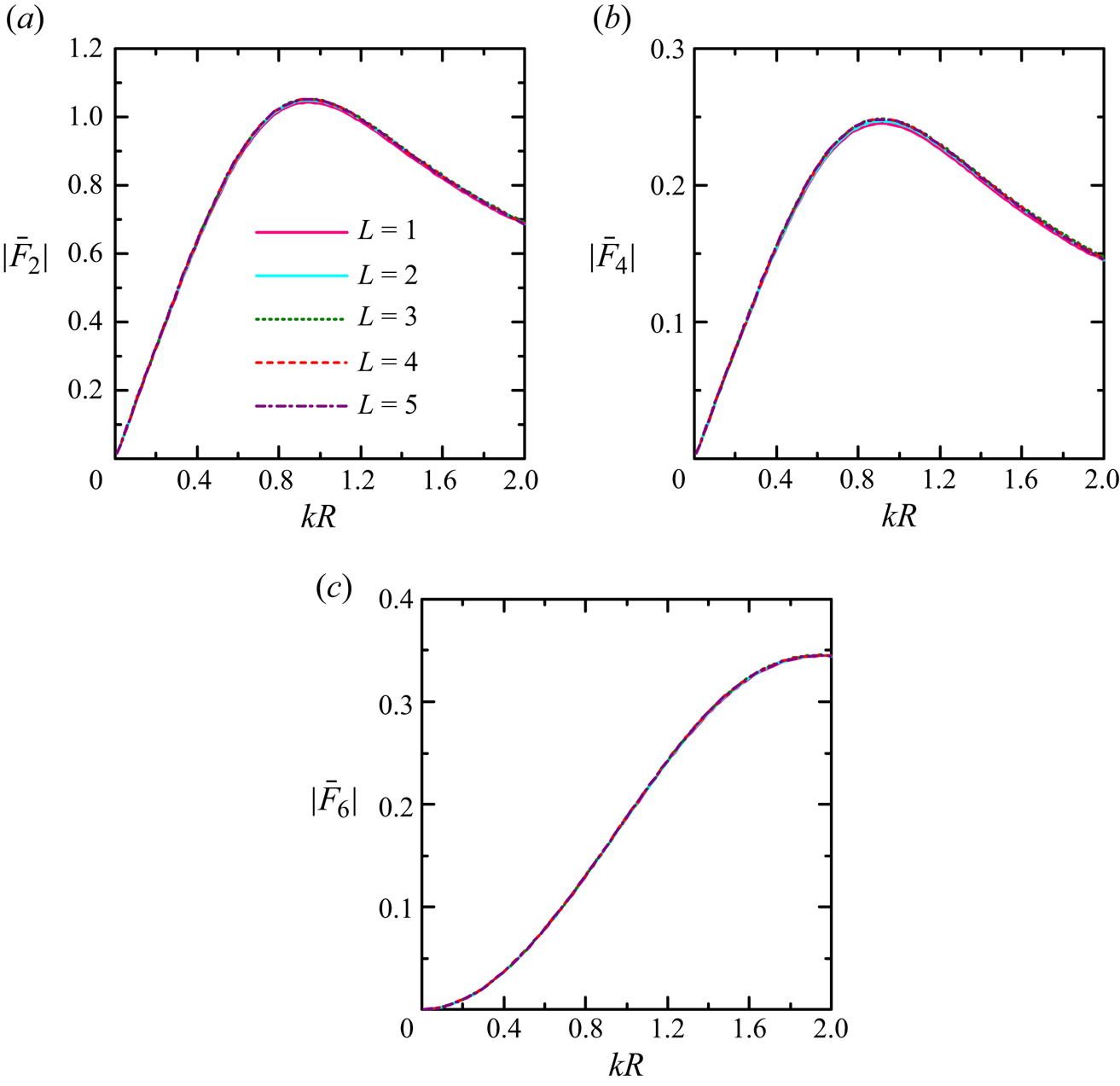
Figure 18. Impact of the vertical cut-offs (i.e. in terms of ![]() $L$) on wave excitation forces acting on vertical truncated metamaterial cylinder with
$L$) on wave excitation forces acting on vertical truncated metamaterial cylinder with ![]() $R/h=1.0$,
$R/h=1.0$, ![]() $d/h=0.5$,
$d/h=0.5$, ![]() $\bar {v}=1.0$,
$\bar {v}=1.0$, ![]() $\beta ={\rm \pi} /4$, and
$\beta ={\rm \pi} /4$, and ![]() $M=5$: (a)
$M=5$: (a) ![]() $|\bar {F}_2|$; (b)
$|\bar {F}_2|$; (b) ![]() $|\bar {F}_4|$ and (c)
$|\bar {F}_4|$ and (c) ![]() $|\bar {F}_6|$.
$|\bar {F}_6|$.