Hostname: page-component-cd9895bd7-lnqnp Total loading time: 0 Render date: 2024-12-28T22:19:16.188Z Has data issue: false hasContentIssue false
  • English
  • Français

Wavepackets in the velocity field of turbulent jets

Published online by Cambridge University Press:  02 August 2013

André V. G. Cavalieri ,
Daniel Rodríguez ,
Peter Jordan ,
Tim Colonius  and
Yves Gervais
André V. G. Cavalieri*
Affiliation:
Département Fluides, Thermique, Combustion, Institut PPrime, CNRS–Université de Poitiers–ENSMA, Poitiers, France Divisão de Engenharia Aeronáutica, Instituto Tecnológico de Aeronáutica, São José dos Campos, SP, Brazil
Daniel Rodríguez
Affiliation:
Division of Engineering and Applied Science, California Institute of Technology, Pasadena, CA 91125, USA School of Aeronautics, Universidad Politécnica de Madrid, Madrid, Spain
Peter Jordan
Affiliation:
Département Fluides, Thermique, Combustion, Institut PPrime, CNRS–Université de Poitiers–ENSMA, Poitiers, France
Tim Colonius
Affiliation:
Division of Engineering and Applied Science, California Institute of Technology, Pasadena, CA 91125, USA
Yves Gervais
Affiliation:
Département Fluides, Thermique, Combustion, Institut PPrime, CNRS–Université de Poitiers–ENSMA, Poitiers, France
*
†Email address for correspondence: andre@ita.br
Get access Rights & Permissions [Opens in a new window]

Abstract

We study the velocity fields of unforced, high Reynolds number, subsonic jets, issuing from round nozzles with turbulent boundary layers. The objective of the study is to educe wavepackets in such flows and to explore their relationship with the radiated sound. The velocity field is measured using a hot-wire anemometer and a stereoscopic, time-resolved PIV system. The field can be decomposed into frequency and azimuthal Fourier modes. The low-angle sound radiation is measured synchronously with a microphone ring array. Consistent with previous observations, the azimuthal wavenumber spectra of the velocity and acoustic pressure fields are distinct. The velocity spectrum of the initial mixing layer exhibits a peak at azimuthal wavenumbers 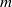$m$ ranging from 4 to 11, and the peak is found to scale with the local momentum thickness of the mixing layer. The acoustic pressure field is, on the other hand, predominantly axisymmetric, suggesting an increased relative acoustic efficiency of the axisymmetric mode of the velocity field, a characteristic that can be shown theoretically to be caused by the radial compactness of the sound source. This is confirmed by significant correlations, as high as 10 %, between the axisymmetric modes of the velocity and acoustic pressure fields, these values being significantly higher than those reported for two-point flow–acoustic correlations in subsonic jets. The axisymmetric and first helical modes of the velocity field are then compared with solutions of linear parabolized stability equations (PSE) to ascertain if these modes correspond to linear wavepackets. For all but the lowest frequencies close agreement is obtained for the spatial amplification, up to the end of the potential core. The radial shapes of the linear PSE solutions also agree with the experimental results over the same region. The results suggests that, despite the broadband character of the turbulence, the evolution of Strouhal numbers 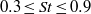$0. 3\leq St\leq 0. 9$ and azimuthal modes 0 and 1 can be modelled as linear wavepackets, and these are associated with the sound radiated to low polar angles.

JFM classification

Instability: Absolute/convective instability Acoustics: Hydrodynamic noise Acoustics: Jet noise
Type
Papers
Information
Journal of Fluid Mechanics , Volume 730 , 10 September 2013 , pp. 559 - 592
Copyright
©2013 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Armstrong, R. R., Fuchs, H. V. & Michalke, A. 1977 Coherent structures in jet turbulence and noise. AIAA J. 15, 1011–1017.Google Scholar
Atvars, J., Schubert, L. K. & Ribner, H. S. 1965 Refraction of sound from a point source placed in an air jet. J. Acoust. Soc. Am. 37 (1), 168–170.CrossRefGoogle Scholar
Batchelor, G. K. & Gill, A. E. 1962 Analysis of the stability of axisymmetric jets. J. Fluid Mech. 14 (4), 529–551.Google Scholar
Becker, H. A. & Massaro, T. A. 1968 Vortex evolution in a round jet. J. Fluid Mech. 31 (3), 435–448.Google Scholar
Bogey, C. & Bailly, C. 2007 An analysis of the correlations between the turbulent flow and the sound pressure fields of subsonic jets. J. Fluid Mech. 583, 71–97.CrossRefGoogle Scholar
Bogey, C., Marsden, O. & Bailly, C. 2011 Large-eddy simulation of the flow and acoustic fields of a Reynolds number 105 subsonic jet with tripped exit boundary layers. Phys. Fluids 23, 035104.CrossRefGoogle Scholar
Breakey, D. E. S., Jordan, P., Cavalieri, A. V. G., Léon, O., Zhang, M., Lehnasch, G., Colonius, T. & Rodríguez, D. 2013 Near-field wavepackets and the far-field sound of a subsonic jet. In 19th AIAA/CEAS Aeroacoustics Conference, Berlin, Germany, AIAA Paper 2013-2083.Google Scholar
Cavalieri, A. V. G., Jordan, P., Agarwal, A. & Gervais, Y. 2011 Jittering wave-packet models for subsonic jet noise. J. Sound Vib. 330 (18–19), 4474–4492.Google Scholar
Cavalieri, A. V. G., Jordan, P., Colonius, T. & Gervais, Y. 2012 Axisymmetric superdirectivity in subsonic jets. J. Fluid Mech. 704, 388–420.Google Scholar
Cohen, J. & Wygnanski, I. 1987 The evolution of instabilities in the axisymmetric jet. Part 1. The linear growth of disturbances near the nozzle. J. Fluid Mech. 176, 191–219.Google Scholar
Crighton, D. G. & Gaster, M. 1976 Stability of slowly diverging jet flow. J. Fluid Mech. 77 (2), 397–413.CrossRefGoogle Scholar
Crow, S. C. 1972 Acoustic gain of a turbulent jet. In Phys. Soc. Meeting, Univ. Colorado, Boulder, paper IE, vol. 6.Google Scholar
Crow, S. C. & Champagne, F. H. 1971 Orderly structure in jet turbulence. J. Fluid Mech. 48 (3), 547–591.CrossRefGoogle Scholar
Delville, J. 1995 La décomposition orthogonale aux valeurs propres et l’analyse de l’organisation tridimensionnelle des écoulements turbulents cisaillés libres. PhD thesis, Université de Poitiers.Google Scholar
Fuchs, H. V. & Michel, U. 1978 Experimental evidence of turbulent source coherence affecting jet noise. AIAA J. 16 (9), 871–872.CrossRefGoogle Scholar
Gudmundsson, K. & Colonius, T. 2011 Instability wave models for the near-field fluctuations of turbulent jets. J. Fluid Mech. 689, 97–128.Google Scholar
Herbert, T. 1997 Parabolized stability equations. Annu. Rev. Fluid Mech. 29 (1), 245–283.CrossRefGoogle Scholar
Hussain, A. K. M. F. & Zaman, K. B. M. Q. 1981 The ‘preferred mode’ of the axisymmetric jet. J. Fluid Mech. 110, 39–71.Google Scholar
Jordan, P. & Colonius, T. 2013 Wave packets and turbulent jet noise. Annu. Rev. Fluid Mech. 45 (1), 173–195.Google Scholar
Jung, D., Gamard, S. & George, W. K. 2004 Downstream evolution of the most energetic modes in a turbulent axisymmetric jet at high Reynolds number. Part 1. The near-field region. J. Fluid Mech. 514, 173–204.Google Scholar
Juvé, D., Sunyach, M. & Comte-Bellot, G. 1979 Filtered azimuthal correlations in the acoustic far field of a subsonic jet. AIAA J. 17, 112–113.Google Scholar
Juvé, D., Sunyach, M. & Comte-Bellot, G. 1980 Intermittency of the noise emission in subsonic cold jets. J. Sound Vib. 71, 319–332.Google Scholar
Kerhervé, F., Jordan, P., Cavalieri, A. V. G., Delville, J., Bogey, C. & Juvé, D. 2012 Educing the source mechanism associated with downstream radiation in subsonic jets. J. Fluid Mech. 710, 606–640.Google Scholar
Kœnig, M. 2011 Réduction de bruit de jet par injection fluidique en corps central tournant. PhD thesis, Université de Poitiers.Google Scholar
Kœnig, M., Cavalieri, A. V. G., Jordan, P., Delville, J., Gervais, Y. & Papamoschou, D. 2013 Farfield filtering and source imaging of subsonic jet noise. Journal of Sound and Vibration 332 (18), 4067–4088.Google Scholar
Kœnig, M., Fourment-Cazenave, C., Jordan, P. & Gervais, Y. 2011b Jet noise reduction by fluidic injection from a rotating plug. In 17th AIAA/CEAS Aeroacoustics Conference, Portland, OR, USA.CrossRefGoogle Scholar
Lau, J. C., Fisher, M. J. & Fuchs, H. V. 1972 The intrinsic structure of turbulent jets. J. Sound Vib. 22 (4), 379–384.Google Scholar
Laufer, J. & Yen, T.-C. 1983 Noise generation by a low-Mach-number jet. J. Fluid Mech. 134, 1–31.CrossRefGoogle Scholar
Lee, H. K. & Ribner, H. S. 1972 Direct correlation of noise and flow of a jet. J. Acoust. Soc. Am. 52, 1280–1290.Google Scholar
Lighthill, M. J. 1952 On sound generated aerodynamically. Part 1. General theory. Proc. R. Soc. Lond. A 564–587.Google Scholar
Maestrello, L. 1976 Two-point correlations of sound pressure in the far field of a jet: experiment. NASA Tech. Rep. TM X-72835.CrossRefGoogle Scholar
Mankbadi, R. & Liu, J. T. C. 1981 A study of the interactions between large-scale coherent structures and fine-grained turbulence in a round jet. Phil. Trans. R. Soc. Lond. A 298 (1443), 541–602.Google Scholar
Mankbadi, R. & Liu, J. T. C. 1984 Sound generated aerodynamically revisited: large-scale structures in a turbulent jet as a source of sound. Phil. Trans. R. Soc. Lond. A 311 (1516), 183–217.Google Scholar
Michalke, A. 1970 A wave model for sound generation in circular jets. Tech. Rep., Deutsche Luft- und Raumfahrt.Google Scholar
Michalke, A. 1971 Instabilität eines kompressiblen runden Freistrahls unter Berücksichtigung des Einflusses der Strahlgrenzschichtdicke. Z. Flugwiss. 19, 319–328, English translation, NASA TM 75190, 1977.Google Scholar
Michalke, A. & Fuchs, H. V. 1975 On turbulence and noise of an axisymmetric shear flow. J. Fluid Mech. 70, 179–205.CrossRefGoogle Scholar
Mohseni, K. & Colonius, T. 2000 Numerical treatment of polar coordinate singularities. J. Comput. Phys. 157, 787–795.CrossRefGoogle Scholar
Mohseni, K., Colonius, T. & Freund, J. B. 2002 An evaluation of linear instability waves as sources of sound in a supersonic turbulent jet. Phys. Fluids 14, 3593.CrossRefGoogle Scholar
Moore, C. J. 1977 The role of shear-layer instability waves in jet exhaust noise. J. Fluid Mech. 80 (2), 321–367.Google Scholar
Österlund, J. M., Johansson, A. V., Nagib, H. M. & Hites, M. H. 2000 A note on the overlap region in turbulent boundary layers. Phys. Fluids 12 (1), 1–4.Google Scholar
Panda, J., Seasholtz, R. G. & Elam, K. A. 2005 Investigation of noise sources in high-speed jets via correlation measurements. J. Fluid Mech. 537, 349–385.CrossRefGoogle Scholar
Papamoschou, D. 2011 Wavepacket modelling of the jet noise source. In 17th AIAA/CEAS Aeroacoustics Conference, Portland, OR, USA.Google Scholar
Petersen, R. A. & Samet, M. M. 1988 On the preferred mode of jet instability. J. Fluid Mech. 194 (1), 153–173.CrossRefGoogle Scholar
Picard, C. & Delville, J. 2000 Pressure velocity coupling in a subsonic round jet. Intl J. Heat Fluid Flow 21 (3), 359–364.CrossRefGoogle Scholar
Schaffar, M. 1979 Direct measurements of the correlation between axial in-jet velocity fluctuations and far field noise near the axis of a cold jet. J. Sound Vib. 64 (1), 73–83.Google Scholar
Schlichting, H. 1979 Boundary-Layer Theory. McGraw-Hill.Google Scholar
Suponitsky, V., Sandham, N. D. & Morfey, C. L. 2010 Linear and nonlinear mechanisms of sound radiation by instability waves in subsonic jets. J. Fluid Mech. 658, 509–538.Google Scholar
Suzuki, T. & Colonius, T. 2006 Instability waves in a subsonic round jet detected using a near-field phased microphone array. J. Fluid Mech. 565, 197–226.Google Scholar
Tam, C. K. W. & Burton, D. E. 1984 Sound generated by instability waves of supersonic flows. Part 2. Axisymmetric jets. J. Fluid Mech. 138, 273–295.Google Scholar
Tam, C. K. W. & Chen, P. 1994 Turbulent mixing noise from supersonic jets. AIAA J. 32 (9), 1774–1780.Google Scholar
Thompson, K. W. 1987 Time dependent boundary conditions for hyperbolic systems. J. Comput. Phys. 68 (1), 1–24.CrossRefGoogle Scholar
Tinney, C. E., Glauser, M. N. & Ukeiley, L. S. 2008 Low-dimensional characteristics of a transonic jet. Part 1. Proper orthogonal decomposition. J. Fluid Mech. 612, 107–141.Google Scholar
Tinney, C. E. & Jordan, P. 2008 The near pressure field of co-axial subsonic jets. J. Fluid Mech. 611, 175–204.Google Scholar
Tomkins, C. D. & Adrian, R. J. 2005 Energetic spanwise modes in the logarithmic layer of a turbulent boundary layer. J. Fluid Mech. 545, 141–162.Google Scholar
Tutkun, M., George, W. K., Foucaut, J. M., Coudert, S., Stanislas, M. & Delville, J. 2009 In situ calibration of hot wire probes in turbulent flows. Exp. Fluids 46 (4), 617–629.Google Scholar
Violato, D. & Scarano, F. 2011 Three-dimensional evolution of flow structures in transitional circular and chevron jets. Phys. Fluids 23 (12), 124104.Google Scholar
Yule, AJ 1978 Large-scale structure in the mixing layer of a round jet. J. Fluid Mech. 89 (3), 413–432.Google Scholar