Hostname: page-component-cd9895bd7-gbm5v Total loading time: 0 Render date: 2024-12-27T08:35:40.021Z Has data issue: false hasContentIssue false
  • English
  • Français

Weak turbulence theory for rotating magnetohydrodynamics and planetary flows

Published online by Cambridge University Press:  19 September 2014

Sébastien Galtier
Sébastien Galtier*
Affiliation:
Laboratoire de Physique des Plasmas, École Polytechnique, F-91128 Palaiseau CEDEX, France
*
†Email address for correspondence: sebastien.galtier@lpp.polytechnique.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

A weak turbulence theory is derived for magnetohydrodynamics (MHD) under rapid rotation and in the presence of a uniform large-scale magnetic field which is associated with a constant Alfvén velocity 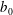$\def \xmlpi #1{}\def \mathsfbi #1{\boldsymbol {\mathsf {#1}}}\let \le =\leqslant \let \leq =\leqslant \let \ge =\geqslant \let \geq =\geqslant \def \Pr {\mathit {Pr}}\def \Fr {\mathit {Fr}}\def \Rey {\mathit {Re}}{\boldsymbol {b}}_{{0}}$. The angular velocity 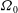${\boldsymbol{\Omega}}_{{0}}$ is assumed to be uniform and parallel to 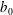${\boldsymbol {b}}_{{0}}$. Such a system exhibits left and right circularly polarized waves which can be obtained by introducing the magneto-inertial length 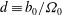$d \equiv b_0/\varOmega _0$. In the large-scale limit (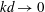$kd \to 0$, with 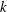$k$ being the wavenumber) the left- and right-handed waves tend to the inertial and magnetostrophic waves, respectively, whereas in the small-scale limit (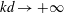$kd \to + \infty $) pure Alfvén waves are recovered. By using a complex helicity decomposition, the asymptotic weak turbulence equations are derived which describe the long-time behaviour of weakly dispersive interacting waves via three-wave interaction processes. It is shown that the nonlinear dynamics is mainly anisotropic, with a stronger transfer perpendicular than parallel to the rotation axis. The general theory may converge to pure weak inertial/magnetostrophic or Alfvén wave turbulence when the large- or small-scale limits are taken, respectively. Inertial wave turbulence is asymptotically dominated by the kinetic energy/helicity, whereas the magnetostrophic wave turbulence is dominated by the magnetic energy/helicity. For both regimes, families of exact solutions are found for the spectra, which do not correspond necessarily to a maximal helicity state. It is shown that the hybrid helicity exhibits a cascade whose direction may vary according to the scale 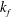$k_f$ at which the helicity flux is injected, with an inverse cascade if 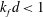$k_fd < 1$ and a direct cascade otherwise. The theory is relevant to the magnetostrophic dynamo, whose main applications are the Earth and the giant planets, such as Jupiter and Saturn, for which a small (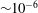${\sim }10^{-6}$) Rossby number is expected.

JFM classification

MHD and Electrohydrodynamics: Dynamo theory MHD and Electrohydrodynamics: MHD turbulence
Type
Papers
Information
Journal of Fluid Mechanics , Volume 757 , 25 October 2014 , pp. 114 - 154
Copyright
© 2014 Cambridge University Press 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

Bardina, J., Ferziger, J. H. & Rogallo, R. S. 1985 Effect of rotation on isotropic turbulence: computation and modelling. J. Fluid Mech. 154, 321–336.Google Scholar
Baroud, C. N., Plapp, B. B., She, Z.-S. & Swinney, H. L. 2002 Anomalous self-similarity in a turbulent rapidly rotating fluid. Phys. Rev. Lett. 88 (11), 114501.Google Scholar
Bartello, P., Metais, O. & Lesieur, M. 1994 Coherent structures in rotating three-dimensional turbulence. J. Fluid Mech. 273, 1–29.Google Scholar
Bellet, F., Godeferd, F. S., Scott, J. F. & Cambon, C. 2006 Wave turbulence in rapidly rotating flows. J. Fluid Mech. 562, 83–121.CrossRefGoogle Scholar
Benney, D. J. & Newell, A. C. 1967 Sequential time closures for interacting random waves. J. Math. Phys. 46, 363–393.Google Scholar
Benney, D. J. & Newell, A. C. 1969 Random wave closures. Stud. Appl. Maths 48, 29–53.Google Scholar
Benney, D. J. & Saffman, P. G. 1966 Nonlinear interactions of random waves in a dispersive medium. Proc. R. Soc. Lond. A 289, 301–320.Google Scholar
Berhanu, M., Monchaux, R., Fauve, S., Mordant, N., Pétrélis, F., Chiffaudel, A., Daviaud, F., Dubrulle, B., Marié, L., Ravelet, F., Bourgoin, M., Odier, P., Pinton, J.-F. & Volk, R. 2007 Magnetic field reversals in an experimental turbulent dynamo. Europhys. Lett. 77, 59001.Google Scholar
Bigot, B. & Galtier, S. 2011 Two-dimensional state in driven magnetohydrodynamic turbulence. Phys. Rev. E 83 (2), 026405.Google Scholar
Bigot, B., Galtier, S. & Politano, H. 2008 Development of anisotropy in incompressible magnetohydrodynamic turbulence. Phys. Rev. E 78 (6), 066301.Google Scholar
Bourouiba, L. 2008 Discreteness and resolution effects in rapidly rotating turbulence. Phys. Rev. E 78 (5), 056309.Google Scholar
Braginsky, S. I. & Roberts, P. H. 1995 Equations governing convection in Earth’s core and the geodynamo. Geophys. Astrophys. Fluid Dyn. 79, 1–97.Google Scholar
Brandenburg, A. 2001 The inverse cascade and nonlinear alpha-effect in simulations of isotropic helical hydromagnetic turbulence. Astrophys. J. 550, 824–840.Google Scholar
Cambon, C. & Jacquin, L. 1989 Spectral approach to non-isotropic turbulence subjected to rotation. J. Fluid Mech. 202, 295–317.Google Scholar
Cambon, C., Mansour, N. N. & Godeferd, F. S. 1997 Energy transfer in rotating turbulence. J. Fluid Mech. 337, 303–332.CrossRefGoogle Scholar
Chen, Q., Chen, S. & Eyink, G. L. 2003a The joint cascade of energy and helicity in three-dimensional turbulence. Phys. Fluids 15, 361–374.Google Scholar
Chen, Q., Chen, S., Eyink, G. L. & Holm, D. D. 2003b Intermittency in the joint cascade of energy and helicity. Phys. Rev. Lett. 90 (21), 214503.CrossRefGoogle ScholarPubMed
Cho, J. 2011 Magnetic helicity conservation and inverse energy cascade in electron magnetohydrodynamic wavepackets. Phys. Rev. Lett. 106 (19), 191104.Google Scholar
Craya, A. 1954 Contribution à l’analyse de la turbulence associée à des vitesses moyennes. (Publications Scientifiques et Techniques du Ministère de l’Air, vol. 345) , Ministère de l’Air, France.Google Scholar
Davidson, P. A. 2004 Turbulence: An Introduction for Scientists and Engineers. Oxford University Press.Google Scholar
Dormy, E., Valet, J.-P. & Courtillot, V. 2000 Numerical models of the geodynamo and observational constraints. Geochem. Geophys. Geosyst. 1, 1037–1042.CrossRefGoogle Scholar
Dyachenko, S., Newell, A. C., Pushkarev, A. & Zakharov, V. E. 1992 Optical turbulence: weak turbulence, condensates and collapsing filaments in the nonlinear Schrödinger equation. Physica D 57, 96–160.Google Scholar
Falcon, É., Laroche, C. & Fauve, S. 2007 Observation of gravity–capillary wave turbulence. Phys. Rev. Lett. 98 (9), 094503.Google Scholar
Favier, B. F. N., Godeferd, F. S. & Cambon, C. 2012 On the effect of rotation on magnetohydrodynamic turbulence at high magnetic Reynolds number. Geophys. Astrophys. Fluid Dyn. 106, 89–111.CrossRefGoogle Scholar
Finlay, C. C. 2008 Waves in the presence of magnetic fields, rotation and convection. In Dynamos, Session 88: Lecture Notes of the Les Houches Summer School 2007 (ed. Cardin, P. & Cugliandolo, L. F.), pp. 403–450. Elsevier.Google Scholar
Finlay, C. C., Dumberry, M., Chulliat, A. & Pais, M. A. 2010 Short timescale core dynamics: theory and observations. Space Sci. Rev. 155, 177–218.Google Scholar
Finlay, C. C. & Jackson, A. 2003 Equatorially dominated magnetic field change at the surface of Earth’s core. Science 300, 2084–2086.CrossRefGoogle ScholarPubMed
Frisch, U. 1995 Turbulence: the Legacy of A. N. Kolmogorov. Cambridge University Press.Google Scholar
Galtier, S. 2003 Weak inertial-wave turbulence theory. Phys. Rev. E 68 (1), 015301.Google Scholar
Galtier, S. 2006a Multi-scale turbulence in the inner solar wind. J. Low Temp. Phys. 145, 59–74.Google Scholar
Galtier, S. 2006b Wave turbulence in incompressible Hall magnetohydrodynamics. J. Plasma Phys. 72, 721–769.Google Scholar
Galtier, S. 2009a Exact vectorial law for homogeneous rotating turbulence. Phys. Rev. E 80, 046301.CrossRefGoogle ScholarPubMed
Galtier, S. 2009b Wave turbulence in magnetized plasmas. Nonlinear Process. Geophys. 16, 83–98.Google Scholar
Galtier, S. 2014 Theory for helical turbulence under fast rotation. Phys. Rev. E 89, 041001(R).CrossRefGoogle ScholarPubMed
Galtier, S. & Bhattacharjee, A. 2003 Anisotropic weak whistler wave turbulence in electron magnetohydrodynamics. Phys. Plasmas 10, 3065–3076.Google Scholar
Galtier, S. & Chandran, B. D. G. 2006 Extended spectral scaling laws for shear-Alfvén wave turbulence. Phys. Plasmas 13 (11), 114505.Google Scholar
Galtier, S. & Nazarenko, S. V. 2008 Large-scale magnetic field sustainment by forced MHD wave turbulence. J. Turbul. 9, 40.Google Scholar
Galtier, S., Nazarenko, S. V., Newell, A. C. & Pouquet, A. 2000 A weak turbulence theory for incompressible magnetohydrodynamics. J. Plasma Phys. 63, 447–488.Google Scholar
Galtier, S., Nazarenko, S. V., Newell, A. C. & Pouquet, A. 2002 Anisotropic turbulence of shear-Alfvén waves. Astrophys. J. Lett. 564, L49–L52.Google Scholar
Glatzmaier, G. A. & Roberts, P. H. 1995 A three-dimensional self-consistent computer simulation of a geomagnetic field reversal. Nature 377, 203–209.Google Scholar
Greenspan, H. P. 1968 The Theory of Rotating Fluids. Cambridge University Press.Google Scholar
Hasselmann, K. 1962 On the nonlinear energy transfer in a gravity-wave spectrum. Part 1. General theory. J. Fluid Mech. 12, 481–500.Google Scholar
Hopfinger, E. J., Gagne, Y. & Browand, F. K. 1982 Turbulence and waves in a rotating tank. J. Fluid Mech. 125, 505–534.Google Scholar
Iroshnikov, P. S. 1964 Turbulence of a conducting fluid in a strong magnetic field. Sov. Astron. 7, 566–571.Google Scholar
Jacquin, L., Leuchter, O., Cambon, C. & Mathieu, J. 1990 Homogeneous turbulence in the presence of rotation. J. Fluid Mech. 220, 1–52.Google Scholar
Jones, C. A. 2011 Planetary magnetic fields and fluid dynamos. Annu. Rev. Fluid Mech. 43, 583–614.Google Scholar
Kingsep, A. S., Chukbar, K. V. & Yankov, V. V. 1990 Electron magnetohydrodynamics. In Reviews of Plasma Physics, Volume 16 (ed. Kadomtsev, B. B.), pp. 243–291. Consultants Bureau.Google Scholar
Kolmakov, G. V., Levchenko, A. A., Brazhnikov, M. Y., Mezhov-Deglin, L. P., Silchenko, A. N. & McClintock, P. V. 2004 Quasiadiabatic decay of capillary turbulence on the charged surface of liquid hydrogen. Phys. Rev. Lett. 93 (7), 074501.Google Scholar
Kraichnan, R. H. 1965 Inertial range spectrum in hydromagnetic turbulence. Phys. Fluids 8, 1385–1387.Google Scholar
Kraichnan, R. H. 1973 Helical turbulence and absolute equilibrium. J. Fluid Mech. 59, 745–752.Google Scholar
Kuznetsov, E. A. 1972 Turbulence of ion sound in a plasma located in a magnetic field. Sov. Phys. JETP 35, 310–314.Google Scholar
Lamriben, C., Cortet, P.-P. & Moisy, F. 2011 Direct measurements of anisotropic energy transfers in a rotating turbulence experiment. Phys. Rev. Lett. 107 (2), 024503.Google Scholar
Lehnert, B. 1954 Magnetohydrodynamic waves under the action of the coriolis force. Astrophys. J. 119, 647.Google Scholar
Lesieur, M. 1997 Turbulence in Fluids, 3rd edn. Kluwer.Google Scholar
Lvov, Y., Nazarenko, S. & West, R. 2003 Wave turbulence in Bose–Einstein condensates. Physica D 184, 333–351.Google Scholar
Matthaeus, W. H. & Goldstein, M. L. 1982 Measurement of the rugged invariants of magnetohydrodynamic turbulence in the solar wind. J. Geophys. Res. 87, 6011–6028.Google Scholar
Meyrand, R. & Galtier, S. 2012 Spontaneous chiral symmetry breaking of Hall MHD turbulence. Phys. Rev. Lett. 109, 194501.Google Scholar
Mininni, P. D. & Pouquet, A. 2009 Helicity cascades in rotating turbulence. Phys. Rev. E 79 (2), 026304.Google Scholar
Mininni, P. D. & Pouquet, A. 2010a Rotating helical turbulence. I. Global evolution and spectral behavior. Phys. Fluids 22 (3), 035105.Google Scholar
Mininni, P. D. & Pouquet, A. 2010b Rotating helical turbulence. II. Intermittency, scale invariance, and structures. Phys. Fluids 22 (3), 035106.Google Scholar
Mininni, P. D., Rosenberg, D. & Pouquet, A. 2012 Isotropization at small scales of rotating helically driven turbulence. J. Fluid Mech. 699, 263–279.Google Scholar
Moffatt, H. K. 1969 The degree of knottedness of tangled vortex lines. J. Fluid Mech. 35, 117–129.Google Scholar
Moffatt, H. K. 1970 Dynamo action associated with random inertial waves in a rotating conducting fluid. J. Fluid Mech. 44, 705–719.Google Scholar
Moffatt, H. K. 1972 An approach to a dynamic theory of dynamo action in a rotating conducting fluid. J. Fluid Mech. 53, 385–399.Google Scholar
Moffatt, H. K. 1978 Magnetic Field Generation in Electrically Conducting Fluids. Cambridge University Press.Google Scholar
Morin, J., Dormy, E., Schrinner, M. & Donati, J.-F. 2011 Weak- and strong-field dynamos: from the Earth to the stars. Mon. Not. R. Astron. Soc. 418, L133–L137.Google Scholar
Morize, C., Moisy, F. & Rabaud, M. 2005 Decaying grid-generated turbulence in a rotating tank. Phys. Fluids 17 (9), 095105.Google Scholar
Nazarenko, S. 2011 Wave Turbulence, Lecture Notes in Physics, vol. 825. Springer.Google Scholar
Newell, A. C., Nazarenko, S. & Biven, L. 2001 Wave turbulence and intermittency. Physica D 152, 520–550.Google Scholar
Parker, E. N. 1958 Dynamics of the interplanetary gas and magnetic fields. Astrophys. J. 128, 664–676.Google Scholar
Perez, J. C. & Boldyrev, S. 2008 On weak and strong magnetohydrodynamic turbulence. Astrophys. J. Lett. 672, L61–L64.Google Scholar
Pétrélis, F., Mordant, N. & Fauve, S. 2007 On the magnetic fields generated by experimental dynamos. Geophys. Astrophys. Fluid Dyn. 101, 289–323.Google Scholar
Pouquet, A., Frisch, U. & Leorat, J. 1976 Strong MHD helical turbulence and the nonlinear dynamo effect. J. Fluid Mech. 77, 321–354.Google Scholar
Rieutord, M., Triana, S. A., Zimmerman, D. S. & Lathrop, D. P. 2012 Excitation of inertial modes in an experimental spherical Couette flow. Phys. Rev. E 86 (2), 026304.Google Scholar
Roberts, P. H. & King, E. M. 2013 On the genesis of the Earth’s magnetism. Rep. Prog. Phys. 76 (9), 096801.Google Scholar
Sagdeev, R. Z. & Galeev, A. A. 1969 Nonlinear Plasma Theory, W.A. Benjamin.Google Scholar
Sahraoui, F., Galtier, S. & Belmont, G. 2007 On waves in incompressible Hall magnetohydrodynamics. J. Plasma Phys. 73, 723–730.Google Scholar
Schmitt, D., Alboussière, T., Brito, D., Cardin, P., Gagnière, N., Jault, D. & Nataf, H.-C. 2008 Rotating spherical Couette flow in a dipolar magnetic field: experimental study of magneto-inertial waves. J. Fluid Mech. 604, 175–197.Google Scholar
Scott, J. F. 2014 Wave turbulence in a rotating channel. J. Fluid Mech. 741, 316–349.Google Scholar
Shaikh, D. & Zank, G. P. 2005 Driven dissipative whistler wave turbulence. Phys. Plasmas 12 (12), 122310.Google Scholar
Shebalin, J. V. 2006 Ideal homogeneous magnetohydrodynamic turbulence in the presence of rotation and a mean magnetic field. J. Plasma Phys. 72, 507–524.Google Scholar
Shirley, J. H. & Fairbridge, R. W. 1997 Encyclopedia of Planetary Sciences. Springer.Google Scholar
Smith, L. M. & Lee, Y. 2005 On near resonances and symmetry breaking in forced rotating flows at moderate Rossby number. J. Fluid Mech. 535, 111–142.Google Scholar
Smith, L. M. & Waleffe, F. 1999 Transfer of energy to two-dimensional large scales in forced, rotating three-dimensional turbulence. Phys. Fluids 11, 1608–1622.Google Scholar
Stanley, S. & Bloxham, J. 2006 Numerical dynamo models of Uranus’ and Neptune’s magnetic fields. Icarus 184, 556–572.Google Scholar
Stevenson, D. J. 2003 Planetary magnetic fields. Earth Planet. Sci. Lett. 208, 1–11.Google Scholar
Tassoul, J.-L. 2000 Stellar Rotation. Cambridge University Press.Google Scholar
Teitelbaum, T. & Mininni, P. D. 2009 Effect of helicity and rotation on the free decay of turbulent flows. Phys. Rev. Lett. 103 (1), 014501.Google Scholar
Turner, L. 2000 Using helicity to characterize homogeneous and inhomogeneous turbulent dynamics. J. Fluid Mech. 408, 205–238.Google Scholar
van Bokhoven, L. J. A., Clercx, H. J. H., van Heijst, G. J. F. & Trieling, R. R. 2009 Experiments on rapidly rotating turbulent flows. Phys. Fluids 21 (9), 096601.Google Scholar
Waleffe, F. 1992 The nature of triad interactions in homogeneous turbulence. Phys. Fluids 4, 350–363.CrossRefGoogle Scholar
Waleffe, F. 1993 Inertial transfers in the helical decomposition. Phys. Fluids 5, 677–685.Google Scholar
Zakharov, V. E. 1965 Weak turbulence in media with a decay spectrum. J. Appl. Mech. Tech. Phys. 6, 22–24.Google Scholar
Zakharov, V. E. 1967 On the spectrum of turbulence in plasma without magnetic field. J. Expl Theor. Phys. 24, 455–459.Google Scholar
Zakharov, V. E. & Filonenko, N. N. 1966 The energy spectrum for stochastic oscillations of a fluid surface. Dokl. Akad. Nauk SSSR 170, 1292–1295.Google Scholar
Zakharov, V. E., L’Vov, V. S. & Falkovich, G. 1992 Kolmogorov Spectra of Turbulence I: Wave Turbulence, Springer Series in Nonlinear Dynamics. Springer.Google Scholar