Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-26T06:50:23.094Z Has data issue: false hasContentIssue false
  • English
  • Français

The wiggling trajectories of bacteria

Published online by Cambridge University Press:  15 June 2012

Yunkyong Hyon ,
Marcos ,
Thomas R. Powers ,
Roman Stocker  and
Henry C. Fu
Yunkyong Hyon
Affiliation:
Department of Mechanical Engineering, University of Nevada, Reno, NV 89557, USA
Marcos
Affiliation:
School of Mechanical and Aerospace Engineering, Nanyang Technological University, Singapore 639798, Singapore
Thomas R. Powers
Affiliation:
School of Engineering and Department of Physics, Brown University, Providence, RI 02912, USA
Roman Stocker
Affiliation:
Ralph M. Parsons Laboratory, Department of Civil and Environmental Engineering, Massachusetts Institute of Technology, Cambridge, MA 02139, USA
Henry C. Fu*
Affiliation:
Department of Mechanical Engineering, University of Nevada, Reno, NV 89557, USA
*
†Email address for correspondence: hfu@unr.edu
Get access Rights & Permissions [Opens in a new window]

Abstract

Many motile bacteria display wiggling trajectories, which correspond to helical swimming paths. Wiggling trajectories result from flagella pushing off-axis relative to the cell body and making the cell wobble. The spatial extent of wiggling trajectories is controlled by the swimming velocity and flagellar torque, which leads to rotation of the cell body. We employ the method of regularized stokeslets to investigate the wiggling trajectories produced by flagellar bundles, which can form at many locations and orientations relative to the cell body for peritrichously flagellated bacteria. Modelling the bundle as a rigid helix with fixed position and orientation relative to the cell body, we show that the wiggling trajectory depends on the position and orientation of the flagellar bundle relative to the cell body. We observe and quantify the helical wiggling trajectories of Bacillus subtilis, which show a wide range of trajectory pitches and radii, many with pitch larger than 4 . 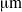For this bacterium, we show that flagellar bundles with fixed orientation relative to the cell body are unlikely to produce wiggling trajectories with pitch larger than 4 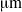. An estimate based on torque balance shows that this constraint on pitch is a result of the large torque exerted by the flagellar bundle. On the other hand, multiple rigid bundles with fixed orientation, similar to those recently observed experimentally, are able to produce wiggling trajectories with large pitches.

JFM classification

Biological Fluid Dynamics: Micro-organism dynamics Biological Fluid Dynamics: Propulsion Biological Fluid Dynamics: Swimming/flying
Type
Papers
Information
Journal of Fluid Mechanics , Volume 705: Special issue dedicated to Professor T. J. Pedley on his 70th birthday , 25 August 2012 , pp. 58 - 76
Copyright
Copyright © Cambridge University Press 2012

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

1. Bearon, R. N. & Pedley, T. J. 2000 Modelling run-and-tumble chemotaxis in a shear flow. Bull. Math. Biol. 62, 775–791.Google Scholar
2. Berg, H. C. & Brown, D. A. 1972 Chemotaxis in Escherichia coli analysed by three-dimensional tracking. Nature 239, 500–504.CrossRefGoogle ScholarPubMed
3. Cortez, R. 2001 The method of regularized Stokeslets. SIAM J. Sci. Comput. 23, 1204–1225.CrossRefGoogle Scholar
4. Cortez, R., Fauci, L. & Medovikov, A. 2005 The method of regularized Stokeslets in three dimensions: analysis, validation, and application to helical swimming. Phys. Fluids 17, 031504.Google Scholar
5. Crenshaw, H. C. 1996 A new look at locomotion in microorganisms: rotating and translating. Am. Zool. 36, 608–618.CrossRefGoogle Scholar
6. Crenshaw, H. C., Ciampaglio, C. N. & McHenry, N. 2000 Analysis of the three-dimensional trajectories of organisms: estimates of velocity, curvature and torsion from positional information. J. Expl Biol. 203, 961–982.Google Scholar
7. Darnton, N., Turner, L., Rojevsky, S. & Berg, H. C. 2007 On torque and tumbling in swimming Escherichia coli . J. Bacteriol. 189, 1756–1764.CrossRefGoogle ScholarPubMed
8. Durham, W. M., Kessler, J. O. & Stocker, R. 2009 Disruption of vertical motility by shear triggers formation of thin phytoplankton layers. Science 323, 1067–1070.Google Scholar
9. Flores, H., Lobaton, E., Méndez-Diez, S., Tlupova, S. & Cortez, R. 2005 A study of bacterial flagellar bundling. Bull. Math. Biol. 67, 137–168.Google Scholar
10. Fujii, M., Shibata, S. & Aizawa, S.-I. 2008 Polar, peritrichous, and lateral flagella belong to three distinguishable flagellar families. J. Mol. Biol. 379, 273–283.CrossRefGoogle ScholarPubMed
11. Goto, T., Masuda, S., Terada, K. & Takano, Y. 1910 Comparison between observation and boundary element analysis of bacterium swimming motion. JSME Intl J. C 44, 958–963.Google Scholar
12. Happel, J. & Brenner, H. 1965 Low Reynolds Number Hydrodynamics. Prentice-Hall.Google Scholar
13. Higdon, J. L. L. 1979 A hydrodynamic analysis of flagellar propulsion. J. Fluid Mech. 90, 685–711.Google Scholar
14. Janssen, P. J. A. & Graham, M. D. 2011 Coexistence of tight and loose bundled states in a model of bacterial flagellar dynamics. Phys. Rev. E 84, 011910.CrossRefGoogle Scholar
15. Keller, J. B. & Rubinow, S. I. 1976 Swimming of flagellated microorganisms. Biophys. J. 16, 151.CrossRefGoogle ScholarPubMed
16. Li, M. 2010 Experimental study of swimming flagellated bacteria and their collective behaviour in concentrated suspensions. PhD thesis, University of Edinburgh.Google Scholar
17. Locsei, J. T. & Pedley, T. J. 2009 Run and tumble chemotaxis in a shear flow: the effect of temporal comparisons, persistence, rotational diffusion, and cell shape. Bull. Math. Biol. 71, 1089–1116.CrossRefGoogle Scholar
18. Magariyama, Y., Ichiba, M., Nakata, K., Baba, K., Ohtani, T. & Kudo, S. 2005 Difference in bacterial motion between forward and backward swimming caused by the wall effect. Biophys. J. 88, 3648–3658.Google Scholar
19. Persson, P. 2005 Mesh generation for implicit geometries. PhD thesis, Massachusetts Institute of Technology.Google Scholar
20. Phan-Thien, N., Tran-Cong, T. & Ramia, M. 1987 A boundary-element analysis of flagellar propulsion. J. Fluid Mech. 184, 533–549.Google Scholar
21. Purcell, E. M. 1977 Life at low Reynolds number. Am. J. Phys. 45, 3–11.CrossRefGoogle Scholar
22. Ramia, M., Tullock, D. L. & Phan-Thien, N. 1993 The role of hydrodynamic interaction in the locomotion of microorganisms. Biophys. J. 65, 755–778.Google Scholar
23. Shapere, A. & Wilczek, F. 1989 Geometry of self-propulsion at low Reynolds number. J. Fluid Mech. 198, 557.Google Scholar
24. Shum, H., Gaffney, E. A. & Smith, D. J. 2010 Modelling bacterial behaviour close to a no-slip plane boundary: the influence of bacterial geometry. J. Fluid Mech. 466, 1725–1748.Google Scholar
25. Smith, D. J., Gaffney, E. A., Gadelha, H., Kapur, N. & Kirkman-Brown, J. C. 2009 Bend propagation in the flagella of migrating human sperm, and its modulation by viscosity. Cell Motil. Cytoskel. 66, 220–236.CrossRefGoogle ScholarPubMed
26. Steinberger, B. N., Petersen, N., Petermann, H. & Weiss, D. G. 1994 Movement of magnetic bacteria in time-varying magnetic fields. J. Fluid Mech. 273, 189–211.CrossRefGoogle Scholar
27. Stocker, R. 2011 Reverse and flick: hybrid locomotion in bacteria. Proc. Natl Acad. Sci. USA 108, 2635–2636.Google Scholar
28. Szurmant, H., Muff, T. & Ordal, G. W. 2004 Bacillus subtilis CheC and FliY are members of a novel class of CheY-P-hydrolyzing proteins in the chemotactic signal transduction cascade. J. Biol. Chem. 279, 21787–21792.Google Scholar
29. Takano, Y., Yoshida, K., Kudo, S., Nishitoba, M. & Magariyama, Y. 2003 Analysis of small deformation of helical flagellum of swimming Vibrio alginolyticus . JSME Intl J. C 46, 1241–1247.Google Scholar
30. Xie, L., Altindal, T., Chattopadhyay, S. & Wu, X.-L. 2011 Bacterial flagellum as a propeller and as a rudder for efficient chemotaxis. Proc. Natl Acad. Sci. 108, 2246–2251.Google Scholar
31. Zimmer, M. A., Szurmant, H., Saulmon, M. M., Collins, M. A., Bant, J. S. & Ordal, G. W. 2002 The role of heterologous receptors in mcpb-mediated signalling in Bacillus subtilis chemotaxis. Mol. Microbiol. 45, 555–568.Google Scholar