Published online by Cambridge University Press: 02 May 2019
The detonation wave structure is analysed in a binary mixture undergoing a reversible chemical reaction represented by 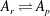 $A_{r}\rightleftharpoons A_{p}$. It is assumed that the flow satisfies the proper basic assumptions of the Zel’dovich–von Neumann–Döring (ZND) detonation model, namely the flow is one-dimensional and the shock is represented by a jump discontinuity, but the assumption of local thermodynamic equilibrium is disregarded. This allows us to deeply investigate the coupling between the detonation structure of overdriven detonations and its chemical kinetics. The thermodynamic non-equilibrium effects are taken into account in the mathematical description, using the model of a multi-temperature mixture developed within extended thermodynamics, which has been proved to be consistent with a kinetic theory approach. The reaction rate is then enriched with terms that take into account the temperatures of the constituents. The results show that the temperature difference between components within the detonation wave structure, which describes thermodynamic non-equilibrium, is driven by the chemical reaction. Numerical computations confirm the existence of non-monotonic profiles in the reaction zone of overdriven detonations which are sensitive to changes in the activation energy and reaction heat.
$A_{r}\rightleftharpoons A_{p}$. It is assumed that the flow satisfies the proper basic assumptions of the Zel’dovich–von Neumann–Döring (ZND) detonation model, namely the flow is one-dimensional and the shock is represented by a jump discontinuity, but the assumption of local thermodynamic equilibrium is disregarded. This allows us to deeply investigate the coupling between the detonation structure of overdriven detonations and its chemical kinetics. The thermodynamic non-equilibrium effects are taken into account in the mathematical description, using the model of a multi-temperature mixture developed within extended thermodynamics, which has been proved to be consistent with a kinetic theory approach. The reaction rate is then enriched with terms that take into account the temperatures of the constituents. The results show that the temperature difference between components within the detonation wave structure, which describes thermodynamic non-equilibrium, is driven by the chemical reaction. Numerical computations confirm the existence of non-monotonic profiles in the reaction zone of overdriven detonations which are sensitive to changes in the activation energy and reaction heat.