Audibility within and Outside Deposited Snow

Abstract

Factors which control the audibility within and outside deposited snow are described and applied to explain the preferential detection of sound by persons buried under avalanche debris as compared to persons on the overlying snow surface. Strong attenuation of acoustic waves in snow and the small acoustic impedance differences between snow and air are responsible for the strong absorption and transmission-loss characteristics that are observed for snow. The absorption and transmission-loss characteristics are independent of the direction of propagation of acoustic signals through the snow. The preferential detection of sound by a person buried under snow can be explained by the relatively higher level of background acoustic noise that exists for persons above the snow surface as compared to an avalanche burial victim. This noise masks sound transmitted to persons on the snow surface, causing a reduction of hearing senstitivity as compared to the burial victim. Additionally, the listening concentration of a buried individual is generally greater than for persons working on the snow surface, increasing their subjective awareness of sound.

Résumé

Les facteurs qui contrôlent l’audibilité à l’intérieur et l’extérieur des couches de neige sont décrits et appliqués à l’explication de la détection préférentielle du son par des individus enfouis sous des avalanches de débris par comparaison aux individus situés sur la surface de la neige. Une forte atténuation des ondes acoustiques dans la neige et une faible différence d’impédance entre la neige et l’air sont responsables des importantes caractéristiques de perte par absorption et transmission. Les caractéristiques de perte en absorption et transmission sont indépendantes de la direction de propagation du signal acoustique dans la neige. La détection préférentielle du son par un individu enfoui sous la neige s’expliquer par le niveau de bruit environnant relativement plus élevé que celui qui existe pour des individus situés sur la surface de la neige en comparaison avec le cas d’une victime enfouie sous l’avalanche. Ce bruit masque le son transmis à la surface en causant une diminution de la sensibilité d’écoute par opposition à la victime enfouie. De plus la concentration d’écoute et la subjectivité d’attention d’un individu enfoui sont généralement plus grandes que celles des individus travaillant à la surface, ce qui accroit leur sensibilité d’écoute.

Zusammenfassung

Einflüsse, welche die Hörbarkeit innerhalb und ausserhalb von Schneeablagerungen regeln, werden beschrieben und zur Erklärung der bevorzugten Schallwahrnehmung von Personen, die unter Lawinen verschüttet sind, im Vergleich zu Personen auf der Schneeoberfläche darüber herangezogen. Die starke Dämpfung von Schallwellen im Schnee und die geringen Unterschiede des akustischen Widerstandes von Schnee und Luft verursachen die grosse Absorption und den Leistungsverlust, wie sie in Schnee zu beobachten sind. Die Charakteristiken der Absorption und des Leistungsverlustes sind unabhängig von der Fortpflanzungsrichtung der Schallsignale im Schnee. Die bevorzugte Schallwahrnehmung von Personen, die unter Schnee verschüttet sind, kann mit dem relativ höheren Geräuschpegel erklärt werden, der für Personen über der Schneeoberfläche im Vergleich zu einem unter einer Lawine begrabenen Opfer vorhanden ist. Die Geräuschkülisse über der Schneeoberfläche verringert die Gehörempfindlichkeit im Vergleich zum Verschütteten. Ausserdem ist die Horchkonzentration und die subjektive Empfänglichkeit für Schall bei einer verschütteten Person im allgemeinen grösser als bei Personen, die auf der Schneeoberfläche arbeiten.

Introduction

Persons who have been buried under deposited snow either intentionally (for example, in a snow cave) or accidentally by an avalanche are well aware of the poor sound-transmission properties of snow and their effect on audibility. These effects are dramatically demonstrated in the accounts of avalanche burial survivors who could hear their rescuers talking and working above them while their shouts for help went unheard (Krasser, 1967; Atwater, 1968; Williams, 1975). In once case, not even four revolver shots fired by a man buried in an avalanche were heard by rescuers (Krasser, 1967).

This preferential detection of sound by avalanche burial victims might imply that acoustic energy transmission in snow is irreversible. Sound propagation in snow, as in other materials, is decidedly reversible in the sense that an acoustic wave propagating along a ray-path will be refracted either toward or away from the axis of incidence, depending on the acoustic properties of a stratified snow cover. Acoustic waves propagating along a ray-path will follow the same path whether their direction is into or out of the snow cover (Fig. 1). Hence, as pointed out by Krasser (1967), attenuation of acoustic energy by viscous processes, internal friction, reflections, and other mechanisms acts in the same manner on waves propagating in either direction along a ray-path. This behavior of acoustic signals is called reciprocity. This means that the acoustic intensity (average rate of energy flow per unit area normal to the direction of propagation) transmitted through snow along a ray-path will be the same regardless of at which end of the ray-path the sound source is located. Consequently, for plane waves, where ray-paths are parallel to each other, the intensity transmitted in either direction across deposited snow will be the same; in a non-attenuating medium, energy contained in a bundle of rays would be constant. The situation for non-planar waves, e.g. spherical waves, is different in that the ray-paths are diverging from each other. Thus, the intensity transmitted across stratified snow will differ depending on the direction of propagation; this is an effect independent of attentuation of the sound energy. For snow with ideal acoustic behavior, propagation of spherical waves in the direction of increasing phase velocity produces more pronounced geometric attenuation than would occur in homogeneous, isotropic snow. Conversely, propagation in the direction of decreasing phase velocity would result in a decreased geometric attenuation (Fig. 1). This implies that velocity gradients may cause differences in audibility between listeners buried under a snow cover and those above the snow. The significance of spherical wave propagation on audibility will be discussed below.

Fig. 1. Refraction of ray-paths through an idealized stratified acoustic material.

• (a) Propagation in the direction of increasing propagation velocity with off-normal incidence;

• (b) Propagation in either the direction of increasing or decreasing propagation velocity;

• (c) Propagation in the direction of decreasing propagation velocity (the dashed lines indicate the ray-path if no refraction were to occur). Propagation velocities are indicated by V ₁, V ₂, V ₃, and V ₄.

There are additional factors that can influence audibility; impedance coupling of a sound source or receiver to snow, refraction of sound in the air above the snow surface, the mechanical interaction of sound waves with the snow, environmental noise, and the physiology of the hearing process. In the following discussion the important factors controlling audibility within and outside deposited snow will be described for both an undisturbed stratified snow cover and avalanche debris. An explanation for the preferential hearing ability described by avalanche burial survivors as compared to persons above the ground will also be given.

Acoustical Phenomena

Acoustic wave interaction with snow

The interaction of acoustic waves with snow is controlled to a large extent by the acoustic impedances of the various materials involved, spatial and geometric attenuation, and snow-cover thickness. The effects of impedance, attenuation, and snow-cover thickness on audibility are best described by the transmission characteristics of snow which can be expressed in terms of a transmission loss TL in decibels. This transmission loss is a measure of the loss of acoustic energy for sound transmitted through the snow and is defined as

(1)

where I _i is the incident intensity, I _t is the transmitted intensity, P _i is the incident pressure, and P _t is the transmitted pressure. In the following, analytical and experimental test results will be used to illustrate the importance of impedance, attenuation, and snow-cover thickness on audibility within and outside snow.

Acoustic impedance for a material is defined as the complex ratio of pressure to particle velocity at a point. If it is independent of position, the impedance is called the wave impedance (W) and is a characteristic parameter of the material. If the particle velocity and pressure are not in phase, the wave impedance is a complex quantity where

W _r is the resistance and is a positive quantity when acoustic energy is transmitted into the snow. W _i is the reactance and depends on the phase difference between the pressure and particle velocity. If W _i = 0, then W is called the characteristic impedance of the material. Wave impedances are often presented as a ratio of that of the reflecting medium (snow) to that of the medium that carries the incident wave (air) where

The characteristic impedance of the air is given by ρ ₀ C ₀, the product of air density and acoustic wave propagation velocity in air. The impedance coupling between adjacent materials determines the manner in which acoustic waves are transmitted and reflected at boundaries separating the different materials. This influence is important since the ratio of impedances between adjacent materials determines the relative magnitude of acoustic energy that is transmitted into or out of a snow cover from an acoustic source or to an acoustic receiver. Figure 2 shows the transmission losses across a boundary separating two adjacent materials as a function of the impedance ratio of the two materials assuming an idealized acoustic model.

Fig. 2. Transmission loss across the interface between two idealized semi-infinite acoustic materials as a function of impedance ratio ξ = W_2r/W₁.

The assumptions of the model are that acoustic signals are transmitted with normal incidence from one semi-infinite material with characteristic impedance W ₁ into a second idealized semi-infinite material with a complex impedance of W ₂ = W _2r + iW _2i. The transmission loss across the boundary separating the two materials is given by (Kinsler and Frey, 1962)

(2)

Equation (2) can be rewritten to show the importance of the ratio of impedances as

(3)

where ξ = W _2r /W ₁ and η = W _2i/W ₁. Figure 2 shows that transmission losses across the interface are controlled by both ξ and η. Typically ξ has a much larger range than does η. The plot also shows that the transmission losses increase symmetrically about ξ _min where . This indicates that it is the impedance ratio that controls the transmission loss and not the magnitude of impedance.

Measured wave impedances have been reported by Johnson (1982, unpublished) for snow with densities from 200 kg/m³ to 420 kg/m³. These measurements indicate that the impedance ratios between snow and air are relatively small, varying from less than one to five. Transmission losses for acoustic waves propagating from air into snow, calculated using impedance data from Johnson (1982) and Equation (3), are plotted on Figure 2. Transmission losses for waves propagating from steel into snow and steel into air have also been plotted in Figure 2. These illustrate that the transmission losses across an air/snow interface are relatively small when compared to other material combinations. These results also imply that high-impedance acoustic sources and receivers would have relatively large transmission losses as compared to acoustic wave transmission across air/snow or snow/air interfaces.

Attenuation of acoustic waves can also strongly affect the transmission loss through a layer of snow. Johnson (1982) used experiments and an analytical model describing the acoustical properties of snow to examine acoustic attenuation in snow. These results indicate that an air pressure-wave is strongly attenuated near the snow/air interface. Over 80% of the acoustic energy transmitted into a homogeneous, isotropic snow-cover can be lost within 1 m of the air/snow interface. Lang (1976) and Ishida (1965) have also conducted experiments that indicate strong acoustic attenuation characteristics for snow. Their results imply that acoustic attenuation strongly contributes to transmission losses. The preceding discussion indicates that the relatively large acoustic absorption characteristics observed for snow can be attributed to pronounced attenuation in snow of acoustic waves that propagate across the air/snow interface with relatively low transmission loss.

The influence of snow-layer thickness on transmission losses is complicated, since variations in layer thickness affect both the overall impedance and the magnitude of acoustic attenuation. Ishida (1965) conducted a series of transmission-loss experiments on homogeneous snow of different thicknesses ranging from 0.02 m to 0.1 m using a white noise source. Ishida’s results indicate that transmission losses increase with sample thickness. The magnitude of transmission loss increase per unit thickness added to a snow layer decreased as the total snow-layer thickness increased. Ishida’s results also indicate that the transmission losses in snow are large, in excess of 200 db/m for his experiments, and strongly controlled by the air permeability. Snow samples with a relatively low air permeability as compared to a second snow sample at the same density were found to have larger transmission losses.

Johnson (unpublished) adapted Biot’s (1956[a], [b]) acoustic porous-media model to investigate the transmission-loss characteristics of snow. A general discussion of the theory and comparison with available experimental data were given by Johnson (1982, unpublished) and will not be repeated here. The model description assumed a vertically stratified snow-pack bounded on both sides by air. This geometry was chosen as an approximate representation of an experimental set-up used by Johnson (unpublished) to represent an avalanche burial victim. An acoustic source generating spherical waves was located a given distance away from the snow surface. The method of images was used to calculate the transmission losses across the snow-pack for the axis normal to the snow surface. A spherical wave source was chosen, since sound generated by people speaking and other sources near a snow surface may well be non-planar. Also the distance above the snow surface of the source can be increased to estimate the plane-wave transmission losses (Fig. 3). Two aspects of spherical wave propagation were examined: (1) the effect of distance between sound source and snow surface, and (2) the effect of direction of propagation across a stratified snow-cover.

Fig. 3. Solution scheme for sound transmission across a layered snow-pack for spherical waves. The wave potential solutions are given by ϕ_j. The layer thicknesses are given by, ℓ, a_K are the boundary locations, and s and s′ are the acoustic source and image source, respectively.

The impedance for spherical waves in a medium is spatially dependent, reducing to the plane-wave case as H → ∞. Figure 4 shows the effect of source distance (that is, the effect of spatially dependent impedance) above a two-layer snow-cover. As the distance between the source and snow surface was increased, the transmission losses across the snow-cover decreased to the plane-wave value. Transmission losses were also calculated for acoustic waves propagating in the opposite direction across the layers, that is layers one and two were reversed. The transmission losses were lower than for case one, less than 1% difference, but not enough to show on the plot. The plane-wave transmission losses across the snow layers were the same in both directions.

Fig. 4. Predicted transmission loss for spherical waves with normal incidence to the air/snow interface as the distance from the sound source to the snow surface increases for a two-layer snow-pack. For layers (a) and (b):

• (1) ρ = 250 kg/m³, B = 2 × 10⁻⁴ s m³/kg, T = 2.86, ℓ = 0.2 m:

• (2) ρ = 500 kg/m³, B = 0.6 × 10⁻⁴ s m³/kg, T = 2.86, ℓ = 0.2 m where ρ is snow density. B is air permeability, and T is structure factor.

Johnson (unpublished) calculated transmission losses for both stratified snow with layering similar to that found in Nature and for avalanche debris which is in general well mixed. Figure 7 shows calculated normalized transmission losses for naturally deposited snow and avalanche debris. The normalized transmission losses were obtained by dividing the calculated transmission losses by the total thickness of the snow layer of interest. This allows a comparison of the transmission characteristics of snow-packs that have different thicknesses. Curves (a) and (b) in Figure 7 represent the transmission losses across snow layers (a) and (b) shown in Figure 5 and the avalanche-debris curve is the transmission loss for the upper 0.3 m of Figure 6. The parameters used in the calculations are given in Table I. Density and air-permeability values given in Figures 5 and 6 show that avalanche debris is more homogeneous with depth than is naturally deposited snow. The air permeability for avalanche debris tends to be less than for comparable density natural snow as well.

Table I. Parameters used to calculate Transmission Losses shown in Figure 7

Fig. 5. Measured density and air-permeability profiles with depth for naturally deposited snow. Snow density and air-permeability data from layers (a) and (b) were used to calculate transmission losses shown in Figure 7.

Fig. 6. Measured density and air-permeability profiles with depth for avalanche debris.

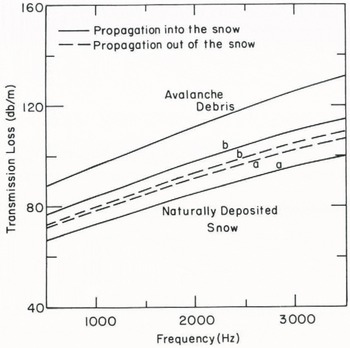
Fig. 7. Calculated normalized transmission loss as a function of frequency for naturally deposited snow (curves a and b) and avalanche debris. The parameters describing the snow used in the calculations are shown in Table I.

Transmission losses for avalanche debris are significantly higher than for naturally deposited snow and exhibit negligible dependence on the direction of propagation. This is due to the relatively low air permeability and homogeneous density of avalanche debris as compared to natural snow. It is also apparent that the effect of propagation direction on transmission losses is more pronounced for natural snow than for avalanche debris (transmission losses for the avalanche debris had no apparent propagation direction dependence). Differences due to propagation direction are relatively small when compared to the total transmission loss through the snow. For curves (a) the transmission loss for acoustic wave propagation out of the snow was calculated to be greater than for propagation into the snow. Conversely, the transmission loss for curves (b) was greater for acoustic wave propagation into the snow as compared to propagation out of the snow. This illustrates that the relative magnitudes for transmission losses cannot be reliably predicted based on propagation direction for naturally deposited snow. The transmission losses depend on the layering structure of a given snow-pack, which can be very complicated. Figure 7 illustrates that transmission losses through snow are very large and that a relatively thin snow layer can greatly reduce the intensity of transmitted sound. Experimental measurements support the calculated results that indicate snow strongly reduces the intensity of sound transmitted through it. Figure 8 shows the normalized transmission losses as a function of frequency measured by Johnson (unpublished) for snow-layer profiles (a) and (b) shown in Figure 5. The overall magnitude of the transmission losses is similar to, but more scattered than, those shown in Figure 7. The influence of sound-source height is readily apparent as transmission losses from H = 0.4 m are significantly lower than for H = 0.2 m in layer (b).

Fig. 8. Experimentally determined normalized transmission loss as a function of frequency for spherical waves in naturally deposited snow. The solid curves represent acoustic wave propagation into the snow and the dashed curves represent propagation out of the snow.

The decrease in transmission losses across a snow layer due to an increased acoustic source height, as shown in Figures 4 and 7, does not mean that more acoustic energy is transmitted across a layer as the source height increases. Transmission loss, as defined by Equation (1), is a relative measure of the acoustic energy transmitted through a snow layer by a wave incident on the snow/air interface. If the acoustic wave energy from two sources, each a different distance from a snow surface, is the same at the snow/air interface (that is the source intensity of the more distance source is larger), then more energy is transmitted by the more distant source. If, however, the acoustic intensity of each source were the same, then the acoustic energy incident on the snow surface would be greater for the nearer source. This would be likely to result in more acoustic energy being transmitted by the source closest to the snow surface. In both cases the transmission losses, as defined by Equation (1), across the snow layer would be less for the more distant source.

The preceding discussion indicates that, for a given sound source, audibility within and outside snow are affected by several factors. The large acoustic absorption and attenuation characteristics of snow result in little reflected acoustic energy and large transmission losses through snow. The effect of propagation direction on the geometric attenuation of non-planar acoustic waves in stratified snow is small compared to the total loss of intensity and insignificant in well-mixed avalanche debris. The large transmission losses for acoustic waves propagating in snow mean that even small layers of snow can greatly reduce audibility across a snow layer. Acoustic wave interaction in snow cannot, however, explain the perceived preferential detection of sound by avalanche burial victims as compared to persons above the snow.

Refraction of acoustic waves in air above a snow surface

Krasser (1967) hypothesized that, since sound propagation in snow is reciprocal (as defined in the Introduction), the preferential detection of sound by avalanche burial victims was caused by processes outside of a snow-cover. He further hypothesized, but did not quantitatively show, that strong temperature inversions and wind-shear-induced velocity gradients in the air just above a snow surface caused sound waves from the snow to refract away from the vertical, causing total reflection at a small height above the snow. Such a total reflection would prevent a person standing on a snow surface from hearing sounds emanating from beneath a snow-cover

Krasser indicated that strong temperature gradients can exist to a height of 0.2 m to 0.5 m above the snow surface, above which are increasingly warmer layers of air. The significance of refraction can be evaluated by estimating both the height at which total reflection occurs and the lateral travel distance of the acoustic wave. These can be determined by using ray-path theory in which Snell’s law is assumed to be valid in the form

(4)

where i is the ray-path angle from the vertical at height Z, V(Z) is the velocity of propagation of sound in air at Z and is assumed to be a continuous function, and P is the ray parameter and is a constant for each ray-path. The geometry described by Equation (4) is shown in Figure 9. The height of total reflection is Z _m and the lateral travel distance for the ray 2X _m. Temperature-caused propagation-velocity changes can be estimated by

(5)

where t ₀ is the temperature at the snow surface in degrees Celsius, V(0) is the propagation velocity of sound in air at the snow surface, a = 0.6 dT/dZ and dT/dZ is the temperature change with height (Kinsler and Frey, 1962). The height of total reflection can be determined by setting i = 90° (that is the ray-path is horizontal) and substituting Equation (5) into Equation (4) giving

(6)

The horizontal travel distance associated with Z _m for a given ray-path can be determined by integrating over dx = tan i dx and is given by

(7)

Substitution of Equation (5) into Equation (7) and integrating gives

The ray parameter is calculated from

where i ₀ is the emergence angle of the ray at Z = 0.

Fig. 9. Ray-path in a vertically inhomogeneous medium where phase velocity is a continuous function of height.

Figure 10 shows Z _m and X _m for emergence angles ranging from 10° to 80°, assuming that t ₀ = 0°C and that the temperature gradient was constant at all values of Z. The assumption of constant temperature gradient produces very conservative estimates of X _m and Z _m. since the temperature gradient should decrease with Z. The effect of refraction of acoustic waves on audibility can be significant only if Z _m is less than the height of a listening person and 2X _m is less than the range of audibility without refraction. The results shown in Figure 10 show that Z _m is in general much greater than 2 m. Even for an extreme temperature gradient of 100 deg/m, Z _m goes below 2 m only for i > 45°. The values for X _m are also quite large with respect to the expected range for a sound source buried in snow. These results would change very little for different values of t ₀. The results shown in Figure 10 indicate that refraction of acoustic waves cannot explain the preferential detection of sound by a person buried under deposited snow. Refraction may, however, contribute to slightly reducing the intensity of acoustic signals reaching a listener by increasing wavefront spreading of non-planar waves.

Fig. 10. Height Z_m above the snow surface lateral distance X_m at which total interal reflection occurs are plotted as a function of emergence angle from the snow surface for various atmospheric temperature gradients, dT/dZ. Refer to Figure 9 for a physical representation of Z_m and X_m.

Conducting an analysis to determine the effects of wind shear on acoustic wave refraction is not warranted. Such winds would have a noise-level masking effect far greater than the refraction of acoustic waves.

Hearing and noise in the environment

The preceding discussion has shown that acoustic waves propagating through snow exhibit large transmission losses. The discussion also indicates that it is highly unlikely that the preferential detection of sound by avalanche burial victims as compared to persons on the overlying snow can be explained solely on the basis of the acoustical properties of snow. This implies that the hearing process for a person and the acoustical environment may be partially responsible for the preferential detection of sound by avalanche burial victims.

The hearing process is subjective and depends on the surrounding noise environment, the level of concentration by the listener, and the auditory capabilities of the ear. The average ear responds to tones covering a frequency range of 20 Hz to over 15 000 Hz and can respond to pressure as small as 10⁻⁵ Pa in a noise-free environment (Kinsler and Frey, 1962). The threshold of hearing in a quiet environment for a normal person is shown in Figure 11. The presence of noise (undesired sound) reduces, in general, the sensitivity of the ear to other sounds and a shift in the threshold of hearing results. This phenomenon is called masking as the noise masks any sound below a threshold intensity level. The masking effects of white noise on the threshold of hearing for a normal person are shown in Figures 11 and 12.

Fig. 11. Idealized masked-threshold contours. These curves show the monaural thresholds of pure tones when masked by various levels of ideal while noise having uniform energy per cycle (Hawkins and Stevens, 1950).

Fig. 12. Relation between masking of pure tones (m) and the effective level of the masking noise. m is the change in the threshold of pure tone due to the noise (Hawkins and Stevens, 1950).

The results shown in Figure 12 indicate that masking noise can significantly decrease hearing sensitivity. This has an important bearing on the phenomenon of the preferential detection of sound in that an individual buried under deposited snow is in an anechoic noise-free environment while persons outside the snow are in a noisy environment. Sources of noise are wind, talking, mechanical equipment, and physical activities associated with working. Table II shows typical noise levels for several different noise environments. Although noise levels above avalanche debris during a rescue have not been measured, it is reasonable to assume they would exceed those found in a broadcast studio (26 db). A 26 db noise level results in a masking of about 25 db (Fig. 12). Noise levels under snow are essentially zero, resulting in a hearing sensitivity difference between listeners on the surface and under snow of 25 db.

Table II. Typical Environment Noise Levels

The relative concentration of a listener can also influence the ability to detect sound. This is particularly relevant to the avalanche burial victim, who may be trying to detect rescue activity. Conversely, rescuers would be directing their attention to search activities and not to listening for sound coming from beneath the snow.

The incident in which an avalanche burial victim fired four revolver shots illustrates the important mechanisms that influence audibility. The victim was buried under more than 6 m of snow. Additionally, rescue workers were using an excavator to dig through the snow (Fraser, 1966). Table II and Figure 12 show that an excavator at work causes masking greater than 80 db at a distance of 15 m from the machinery. The combination of high transmission losses through 6 m of snow, noise masking in excess of 80 db by the excavator, and different levels of concentration between listeners outside and within the snow, explain why the burial victim could hear the rescuers while they could not hear the revolver shots. These mechanisms would also explain less dramatic accounts of avalanche burial survivors hearing their rescuers while going unheard.

Conclusions

Several factors which can affect audibility within and outside deposited snow have been identified and examined. These include refraction of sound due to velocity gradients in the air above the snow, the interaction of sound waves with snow, environmental noise, and the hearing process. Refraction effects outside a snow-cover were found to be insignificant. Interaction of sound waves with snow has the strongest influence on audibility. Impedance matching between a sound source or receiver and snow attenuation of acoustic signals in snow and snow-layer thickness determine the magnitude of transmission losses through a snow layer. Transmission losses are, in general, high for snow. They increase with an increase in density or a decrease in air-permeability and are frequency dependent. Transmission losses for naturally deposited snow are less than for avalanche debris at the same density. This is due to lower air-permeability values for avalanche debris. The transmission losses for non-planar waves in vertically stratified snow vary slightly, depending on whether the wave is propagating in the direction of increasing or decreasing phase velocity. This is a geometric refraction effect that causes the acoustic energy density to decrease more rapidly in the direction of increasing phase velocity than in the direction of decreasing phase velocity. This is a small effect and not reliably detected by experiments. Noise in the environment and the hearing process are additional factors that affect audibility and also help to explain the preferential detection of sound by an avalanche burial victim over rescuers working on the snow surface. Environmental noise, which occurs outside of the snow and not under the snow, acts to mask sound and requires that sound intensity exceed the masking level before a listener can detect it. Additionally, the level of concentration of a listener can influence the intensity level at which a sound is detected.