Avalanche dynamics by Newton. Reply to comments on avalanche flow models based on the concept of random kinetic energy

Abstract

The critique by Issler and other (2017) of our avalanche dynamics model maintains that we disregard well-established results of particulate gravity flows. Here we show that the arguments of Issler and others (1) violate Newton's laws of motion in the avalanche core and (2) ignore size-dependent drag forces on snow particles (Stokes law) that lead to the formation of avalanche suspension layers. We explain why we cannot amend our model equations to accommodate their suggestions. The goal of our approach is to describe highly non-stationary processes in the avalanche core that lead to a wide range of avalanche flow types and therefore different flow behavior. This is important for practical applications.

1. INTRODUCTION

In their recent paper, Issler and others (2017) make three direct charges against our work. Namely (i) the proposed method does not agree with results on dense granular flows, (ii) a third-order equation to describe the slope perpendicular accelerations is in error and (iii) the model for the suspension cloud disregards well-established results on particulate gravity currents and needs substantial adjustments.

Our response to these charges is clear: the arguments invoked by Issler and others (2017) violate Newton's laws of motion, specifically the law of action and reaction. As such, they are a clear mis-statement of our work. Furthermore, avalanche flow involves non-equilibrium processes that cannot be adequately described using quasi-equilibrium mechanics, as Issler and others (2017) seem to suggest. The fluidization of the avalanche core and the formation of the powder cloud require considering flow transitions they may, or may not reach equilibrium. Because we have abandoned quasi-equilibrium flow models, we can accurately describe the movement of dense flowing and powder snow avalanches for many practical applications (Dreier and others, 2016; Stoffel and others, 2016; Bartelt and others, 2017; Margreth and others, 2017).

The paper of Issler and others (2017) therefore provides an excellent opportunity to discuss the state of avalanche modeling, particularly the key problems in avalanche dynamics, firstly the interaction of the core with the basal running surface and secondly the formation and movement of the powder cloud. We wish to express our arguments as clearly and directly as possible. Our hope is that they can be easily grasped by a practicing avalanche engineer. In this way, the concerns of Issler and others (2017) can be explained and resolved. Our yardstick is not agreement to well-established concepts, but to the problem at hand, snow in motion.

2. THE AVALANCHE CORE

In our model for the avalanche core we define a local coordinate system with the x-axis located parallel to the terrain surface. The z-axis is defined perpendicular to the basal plane, Figure 1. In the following, we turn our local x-axis into the flow direction, permitting us to reduce the problem of avalanche flow to one-dimension without losing generality. We consider the movement of avalanche mass $M_{\Phi }(t)$ flowing through regions with fixed sides, which we term flow ‘columns’. The flow height of the column $h_{\Phi }(t)$ varies with time. We measure the flow height $h_{\Phi }(t)$ with respect to the co-volume height $h_0(t)$ , which we assume to represent the densest possible packing of avalanche snow for the mass $M_{\Phi }(t)$ . The column with height $h_{\Phi }$ can expand from or contract to the co-volume $h_0$ . This description allows us to consider instationary processes arising from shearing. By considering the change in acceleration of the center-of-mass (located at the height $k_{\Phi }$ inside the column) we consider states of static equilibrium ( ${\ddot k}_\Phi = 0$ ), ( ${\ddot k}_{\Phi } \ne 0$ and $k^{\cdots}_{\Phi} = 0$ ) and states of dynamic non-equilibrium ( ${\ddot k}_{\Phi} \ne 0$ and $k^{\cdots}_{\Phi}\ne 0$ ). We argue that all the three states are necessary to describe avalanche flow, especially the formation of the powder cloud.

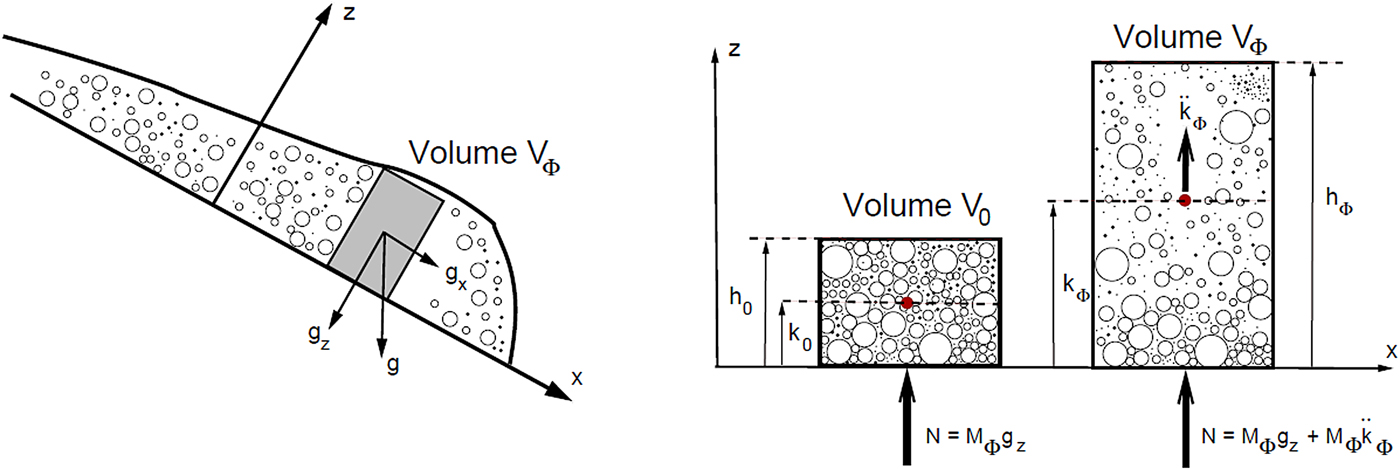
Figure 1. Newton's law of action and reaction applied to a flow column in the avalanche body. Avalanche mass flows in the slope parallel x-direction. The column can expand in the slope perpendicular z-direction. Particulate avalanche mass $M_{\Phi }$ flows through the column; the column sides are fixed and therefore the volume $V_{\Phi }$ can only vary with height. We consider two states: (a) the co-volume, or dense packing of snow granules. The norm of the force on the ground is $N = M_{\Phi } g_z$ . The center-of-mass of the co-volume is located at $k_0$ . (b) During flow the particulate mass $M_{\Phi }$ is sheared and expands due to the acceleration ${\ddot k}_{\Phi }$ . The height of the flow column, defined by the location of the highest particle, is now $h_{\Phi }$ . The center-of-mass moves from $k_0$ to $k_{\Phi }$ . The reaction to the acceleration of the center-of-mass is termed the dispersive pressure $N_k = M_{\Phi } {\ddot k}_{\Phi }$ . No restrictions are made on the timescale of the expansion.

The dispersive pressure $N_k$ , a name first coined by Bagnold (1954), is the excess pressure resulting from the shearing of the snow particles. At first, Issler and others correctly state our definition for $N_k$ (Issler and others, 2017, Eqn (V.4))

(1) $$N_k = M_{\Phi} {\ddot k}_{\Phi}.$$

Because we have a free upper boundary and a fixed lower boundary, the dispersive pressure causes a reaction on the bottom surface due to the upward acceleration of the center-of-mass, Figure 1. This definition of dispersive pressure is valid for both expansion of the column (increasing N _k , ${\ddot k}_{\Phi } \gt $ 0) and when the column contracts (decreasing N _k , ${\ddot k}_{\Phi } \lt 0$ ). We make no assumptions concerning the speed of the expansion or contraction, unlike Issler and others (2017). The volume $V_{\Phi }$ contains random kinetic energy $R_{\rm K} V_{\Phi}$ . The energy density $R_{\rm K}$ represents the kinetic energy associated with random particle movements (Bartelt and others, 2006). Issler and others (2017) state, ‘Buser and Bartelt postulate that the equation of state of a granular snow avalanche is essentially equivalent to that of an ideal gas, i.e. they assume

(2) $$N h_{\Phi} = \gamma R_{\rm K} h_{\Phi}^{\prime}.$$

In this equation, γ is a coefficient relating the random kinetic energy $R_{\rm k}$ to the pressure N. This statement is both (i) physically incorrect and (ii) a mis-statement of our work (see Issler and others, 2017, Eqn (11)). The normal force is defined by Newton's law of action and reaction, not by $R_{\rm K}$ or an analogy to the ideal gas law. If the center-of-mass does not move, then the reaction on the bottom is always equal to the weight $N = M_\Phi g_z$ , independent of the magnitude of random kinetic energy $R_{\rm K}$ (Fig. 2). The particle collisions with the boundary are such that they support the flow in equilibrium $N = M_\Phi g_z$ . This can occur for $R_{\rm K} = 0$ , or any finite value $R_{\rm K} \gt 0$ , (Fig. 2). It does not matter whether we have a solid continuum or a granular continuum. Newton's law holds, i.e., we have

(3) $$ N = M_{\Phi} g_z + M_{\Phi} {\ddot k}_{\Phi}. $$

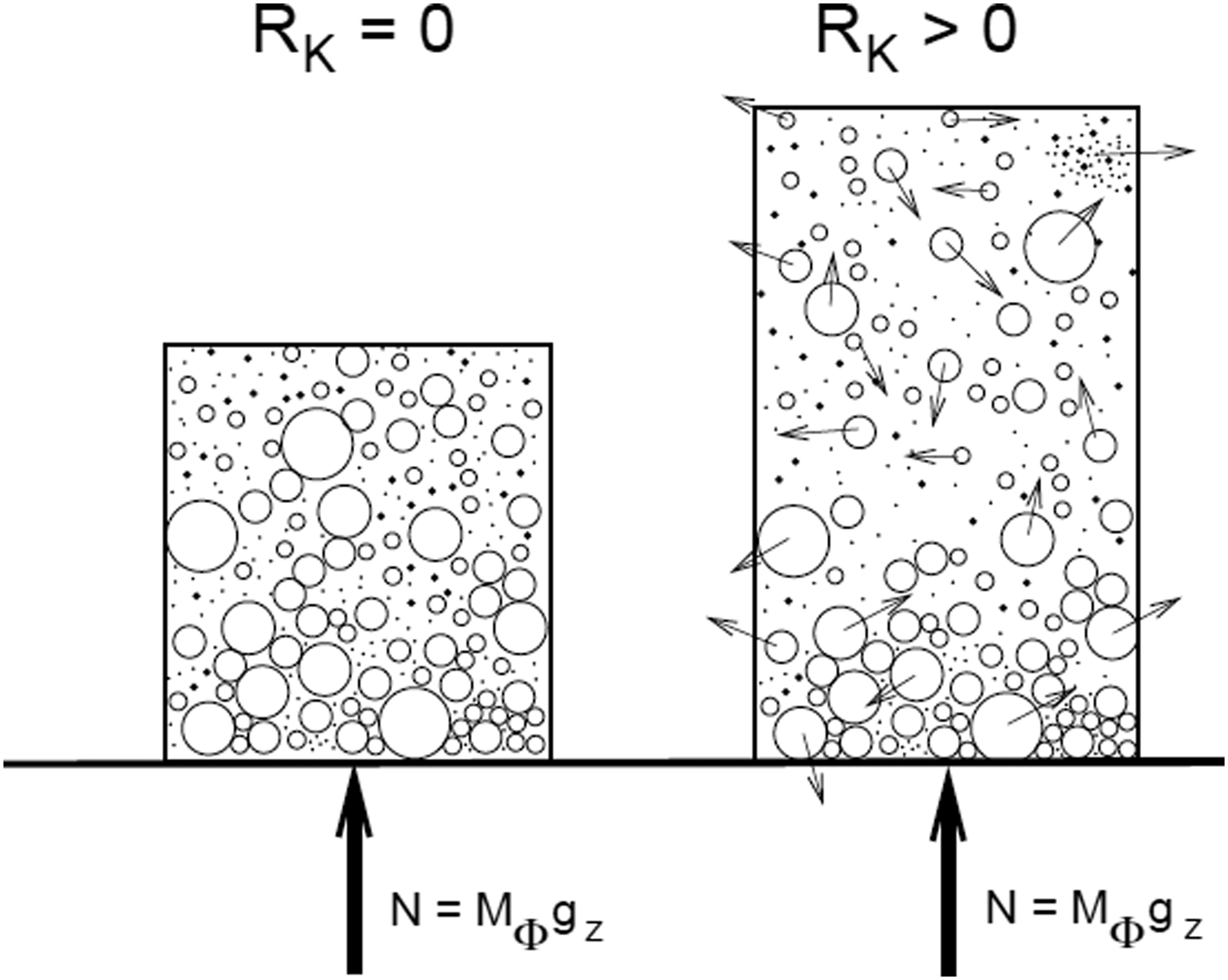
Figure 2. Two columns in the avalanche, both contain the same mass $M_{\Phi }$ . The avalanche column on the left contains no random energy $R_{\rm K}=0$ ; the column on the right contains random energy $R_{\rm K} \gt 0$ . Only when the center-of-mass of the column changes, there will be a change in the normal pressure N. The weight of both masses remains the same $N = M_{\Phi } g_z$ . This is Newton's law of action and reaction. According to Issler and others (2017) the normal force N is proportional to $R_{\rm K}$ .

We repeat: our dispersive pressure is the imbalance between the reaction N and the weight $M_{\Phi } g_z$ . Imagine standing on a bathroom scale and measuring the reaction (your weight), one time standing flat-footed, the next time down in a crouch. In both cases, the weight is measured (although your configuration has changed). Our dispersive pressure is zero in both cases. Only when you change your configuration (move your center-of-mass upwards or downward) does the reading on the scale (the reaction) change. By Newton, it changes in accordance to how quickly your center-of-mass is accelerated.

It is a common mistake to think that the dispersive pressure holds the center-of-mass in place. It is the reaction on the bottom, invoked by the action (the weight) that holds the center-of-mass in place. Moreover, N (reaction)  =  $M_{\Phi } g_z$ (action).

The random kinetic energy $R_{\rm K}$ does not do anything but expand the volume. Once expanded, the center-of-mass does not move anymore and we cannot see any difference in N, both before and after the expansion (or shrinking). Both states have the same mass and therefore the same weight and the same reaction.

Our formulation satisfies the boundary conditions exactly, in accordance with Newton and simple experiments, that when $R_{\rm K} = 0$ , $N_{\rm k} = 0$ and further when $R_{\rm K}$  =  constant, $N_{\rm k} = 0$ . In their formulation Issler and others (2017) forget the reaction on the boundary and assume the random energy $R_{\rm K}$ somehow holds the mass in place. Issler and others assumptions lead them to conclude that the acceleration ${\ddot k}_{\Phi }$ of the center-of-mass can be by given by (see Issler and others, 2017, Eqn (12), but found elsewhere, e.g. Eqn (21))

(4) $${\ddot k}_{\Phi} = \gamma \displaystyle{{R_{\rm K}} \over{M_{\Phi}}} + g_z.$$

This equation disregards the boundary. When $R_{\rm K}=0$ , it implies that ${\ddot k}_{\Phi }$ = $g_z$ and therefore the mass is in free fall (no boundary). This is not a ‘strong assumption’ of our theory, but a mis-statement.

More importantly, Issler and others (2017) conclude that only a second-order equation, similar to the above, is needed to describe the avalanche core. We conclude otherwise: the mean normal pressure will differ from the weight only when we have changes in the slope-perpendicular acceleration of the avalanche core ( $k^{\cdots}$ , jerk). In order to track changes in the avalanche core, we must advance to a higher kinematic level to consider jerks and jolts arising from the basal boundary. This is yet another simple consequence of Newton's law.

The changes in slope-perpendicular acceleration can be found by equating a fraction (γ) of the production of random energy ( $\dot P$ ) with the work needed to change the location of the center-of-mass of the avalanche. We simply say that a fraction of the shear-work is used to raise the center-of-mass. For details, see Buser and Bartelt (2009, 2015). Using the definition of substantial derivative,

(5) $$ {\displaystyle {D(NV_\Phi)} \over {Dt}} = \gamma \dot P V_\Phi. $$

The parameter γ is not a coefficient related to the ideal gas law, or an equation of state, as Issler and others (2017) suggest. It is a coefficient that partitions the production of the random energy into a change in both the random kinetic energy and the potential energy in the slope perpendicular direction. This balance equation satisfies energy conservation and also Newton's law. It opens the door to modeling highly non-stationary processes in the avalanche core. We do make the assumption that there is no change in mass during the change in acceleration. This assumption can be (and is) relaxed when we consider snow entrainment.

The only well-established concept of granular mechanics that we invoke (besides Newton) is Reynolds’ result that a sheared granular body dilates (Reynolds, 1885). The shear work rate, a quantity that depends on the avalanche boundary conditions, constrains the energy that is available to change the structure of the core.

3. FRICTION

Issler and others (2017) are clearly uncomfortable with our third-order equation describing changes in slope-perpendicular accelerations (jerks). A third-order equation is necessary because the frictional shear work, the process driving the accelerations, is a slope and terrain dependent function. It depends on time. We cannot exclude sudden changes that occur over short-time intervals (imagine avalanches confronted by sudden changes in terrain and roughness which is the normal case, see Fig. 3). This function is basically unknown, but determines the configuration of the core and therefore flow friction. We must calculate it at discrete time intervals as the avalanche descends considering the local boundary conditions. For this reason, we never can assume stationary flow when discussing models of flow friction.

Figure 3. The avalanche core Φ experiences a continuous series of jolts from the boundary. Shearing $S(x,\,t)$ induces changes in slope-perpendicular accelerations ${\ddot k}_{\Phi }(x,\,t)$ which are an unknown function of position x and time t. The accelerations depend on the speed of the avalanche, as well as external factors such as terrain. The configurational energy of the core $R_V$ , and therefore flow friction, depends on the external forcing, which is a function of x and t. The component of gravity in the x-direction is denoted $g_x$ . It acts on the core mass, not the cloud mass. Large velocity gradients exist between the leading edge and tail (wake) of the powder cloud Π.

Note that our third-order equation can be expressed as a second-order equation in the slope-perpendicular velocity. $\ddot w_{\Phi }={\dot k}_{\Phi}$ ,

(6) $${\ddot w}_{\Phi} + \left [ {\displaystyle {g_z + \dot w_{\Phi}} \over {k_{\Phi}}} \right] w_{\Phi} = {\ddot w}_{\Phi} + \omega^2 w_{\Phi} = \gamma {\displaystyle {\dot P(t) } \over {M_{\Phi}}}. $$

This equation is similar to an undamped, non-linear parametric oscillator. In principle, the external forcing $\dot P(t)$ could be formulated as a Fourier series to identify the frequency content of the forcing. The frequency ω identifies the external input frequency which will fluidize the core; that is, amplify the configurational energy $R_{\rm V}$ . Moreover, whether the avalanche core relaxes (i.e. returns to the co-volume, frictional flow regime) or fluidizes (collisional flow regime) depends on slope angle and the frequency content of the frictional input. We do not describe flow friction using the random kinetic energy $R_{\rm K}$ , rather the configurational energy $R_{\rm V}$ , which is a measure of particle spacing in the core.

Of course, the slope-perpendicular accelerations are damped and therefore the configurational energy $R_{\rm V}$ will decay. One significant damping process is the energy needed to create the suspension layer, which must be removed from the core. Other damping processes exist, for example the compaction (sink-in) of the running surface or the granularization of the snowcover. All will contribute to reducing the accelerations in the slope-perpendicular direction and reducing the configurational energy $R_{\rm V}$ . In the analysis of our friction model, all of these additional damping processes are not considered by Issler and others (2017), leading to the conclusion that friction will simply decrease with velocity. By making the friction coefficients a function of the configurational energy we capture the dissipative effects in the slope-perpendicular direction, which can be significant.

4. SUSPENSION LAYER

Snow mass in avalanches behaves in one of the two distinct ways: if the particle is small enough it is suspended in air; if the particle is large (or if small particles act as a coordinated packet as a whole, clusters) the mass cannot be suspended. It falls back to the ground under the action of gravity, see Figure 4. In our model the mass that can be suspended belongs to the suspension layer; mass that cannot be suspended, belongs by definition to the avalanche core (Bartelt and others, 2016). That is, we separate particulate mass according to how it physically behaves. Moreover,

• • $M_{\Phi }$ , ‘heavy’ mass, non-suspended mass

• • $M_{\Pi }$ , fine particles and air, suspended mass

Figure 4. A representative column in the avalanche. Avalanche mass is divided into suspended mass $M_{\Pi }$ and heavy mass that falls to the ground under gravity $M_{\Phi }$ . The two masses (a) overlap. The suspension layer consists of suspended mass $M_{\Pi }$ (by definition); the avalanche core consists of the gravity driven mass $M_{\Phi }$ . Both layers have the same height measured from the ground. (b) The heavy mass segregates out of the suspension layer. Packets of ice-dust (clusters) may fall under gravity, acting as a coordinated whole and thus belong to the core mass $M_{\Phi }$ .

This definition diverges from the definition of Issler and others (2017). We try to avoid the oxymoron of a ‘gravity-driven suspension current’ in which the suspension cloud contains non-suspendable mass. We separate the suspended mass from the non-suspended mass.

A particle becomes suspended when the downward force of gravity and the particle drag forces (Stokes) almost exactly offset, producing particles that almost do not move relative to the air, see Figure 5. This definition explains the fundamental difference between our model and much of the literature cited by Issler and others (2017) (e.g. Ancey, 2004; Turnbull and McElwaine, 2007): The density difference between the ice grains and air is not the driving force of the suspension cloud, by definition. If it would be so, then we would see a whole host of unusual phenomena. For example, cumulus clouds or banks of fog clinging to mountain cliffs would fall directly from the sky and ravage havoc among the peaceful inhabitants of mountain communities (Fig. 5). Of course, clouds do not fall from the sky (even though the clouds contain huge amounts of mass) because of Stokes drag. The clouds are suspended.

Figure 5. The model of Issler and others (2017) treats suspension clouds as gravity currents. They argue that gravity accelerates a suspension cloud because the density difference between the ice and air is large. Their model predicts, clouds should fall from the sky and reach large velocities. The inclusion of gravity in our model of the suspension cloud is in error because $M_{\Pi }$ contains only mass that can be suspended. That is, we assume no relative movement of the particles with the air g = S. The cloud can only move by accelerating the air containing the ice particles.

One way to visualize the suspension cloud is at the end of an avalanche event when the cloud hangs over the deposits. Note there is a density difference between the ice particles and the air, but the cloud is stationary; the particles sediment slowly, but any wind can sweep the cloud away. The air drives the particles; the particles do not drive the air. The tail of the powder cloud is correctly termed the wake; its non-motion standing in sharp contrast to its formation at the avalanche front, best compared with the formation of the smoke cloud ejected by a fast moving steam engine (Fig. 3). Our model of the suspension layer captures this behavior: we are able to predict the large slope-parallel velocity gradients that exist in the cloud between the avalanche front and wake, as well as the speed of the lateral spreading (Dreier and others, 2016).

In our model, the ‘heavy’ (non-suspendable) mass, with all the associated momentum, never leaves the core. It is part of the core, by definition, because drag forces acting on the larger particles (Stokes) are small relative to gravity. The motion of the core mass is therefore governed by terrain (slope-parallel direction). Our experience with models that do not distinguish between suspended (cloud) and non-suspended mass (core) is that they cannot correctly model the momentum transfer between the cloud and core and therefore cannot be applied to solve problems in practice (Stoffel and others, 2016). These models presuppose clean layers and interfaces where idealized but highly tangled book-keeping operations governing mass and momentum transfer are necessary. We make no such modeling assumptions: suspended and non-suspended mass at first coexist in the core (Fig. 6). The top of the core volume is defined by the location of the highest particle (or cluster of particles) that will fall back to the ground. When mass is accelerated upwards, however, part of this mass becomes suspended to form the cloud. This is the formation of the suspension layer. We try to avoid models where the separation between core and suspension layer is never complete, where it is a messy divorce of ever continuing entanglements of mass and momentum. We enforce the divorce: the suspended mass is given its share of momentum and never returns (because it is suspended and cannot return by definition). The cloud and core are now two completely independent bodies (Fig. 6); the motion of the core defined by gravity; the motion of the cloud defined by inertia and the initial momentum provided by the core. The suspension is now independent of terrain. The engineering problem is to understand over what distance the suspension cloud dissipates the initial energy. This approach allows us to stick to depth-averaged methodologies and, as we have shown, is a practicable approach to modeling the danger of powder snow avalanches.

Figure 6. Our model decouples the suspended and heavy mass, allowing the modeling of both the avalanche front and avalanche wake without imposing artificial interfaces. The avalanche core is defined by the location of the highest heavy particle. This mass never leaves the core, but expands upwards into the suspension layer, often to great heights. Momentum is transferred from the heavy particles to the air giving the suspension layer an initial velocity (initial condition).

It is not necessary to include particle sedimentation (gravity) in the model because it is of little engineering relevance. The particles serve as passive tracers to delineate the shape of the cloud. Therefore, to understand how a suspension cloud moves requires understanding the motion of the air. If the avalanche core can create a wind storm then the suspension layer can cause damage. Otherwise the cloud, like a bank of fog, is harmless. This is often, but not always, the case in practice.

This is why the gravity component can be neglected in our approach to simulate the suspension layer which is simply not a gravity current (again, by definition). Therefore, we do not have to consider any well-established theory which mixes and confuses the physical behavior of a particulate ‘gravity current’ with a ‘suspension layer’. These concepts include Richardson number entrainment, potential flow, shear instabilities etc. The physical processes, including both gravitational and inertial accelerations that govern the motion of a ‘highly turbulent’ gravity current are included in our model of the avalanche core, assuming, of course, that we allow for highly non-stationary behavior.

5. CONCLUSIONS

Here we must be blunt: we have not disregarded the solutions offered by granular mechanics/particulate gravity currents. The situation is far more serious: we have abandoned them for the simple reason we found that they do not work. Confronted with the task of developing an avalanche model for engineering practice we asked ourselves a simple question: what does the consequential application of the laws of Newton and Stokes imply for the all-important descriptions of the basal boundary conditions, avalanche flow friction and the formation of the powder cloud. We wanted to avoid model formulations that abound in needless and misleading jargon, mis-statement, contradiction and general illogic. Above all we wanted a model that can be tested using experimental measurements and that is comprehensible to engineers and technologists.

We came to the remarkable conclusion that the application of Newton's law demands that we consider changes in slope-perpendicular accelerations arising from the interaction of the avalanche core with highly variable terrain. This process, which depends on snow properties, determines avalanche friction. By invoking Newton we could explain why avalanches exhibit different flow regimes. The combined application of the laws of Newton and Stokes allowed us to formulate a model for the formation of the powder cloud, helping us explain under what snow and terrain conditions we must expect damaging impact pressures from the avalanche cloud. We did not set out to do so, but by trying to supply avalanche experts with useful and comprehensible tools, we have rejected a great body of well-established ideas. We strongly suggest that the avalanche community try-out their ideas first on some straight forward case studies. They might find, like us, that some of their ideas do not provide the results they expect.